2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
洪涝灾害破坏强度大,突发性强,后续影响严重,是当今世界最主要的自然灾害类型之一[1]。研究降雨所导致的河流水系的洪涝灾害动态致灾过程,需要深入探索上游水位变化与下游水位上涨之间的关系以及由于下游水位上涨造成的洪涝淹没状况,这对于流域洪水的预警预报、防灾减灾工作有着重大意义[2]。
现有研究证明,河段上下游水位之间存在着良好的响应关系[3-4]。在一次洪水事件中,上游断面发生水位涨落时,下游断面水位会在一定时间后发生同位相涨落。不少学者利用水文站点监测数据分析出这种河道上下游水位间的响应规律来预测下游洪峰水位信息,称作相应水位法[5-8]。此外,国内外水利专家还从洪水演进过程着手,利用水文站点监测数据耦合多种水动力模型预测受灾地区的淹没范围,如Matkan等[9]利用流量水位监测数据标定HEC-RAS模型进而预测Madarsoo河流域的洪水淹没范围,预测总体精度达到0.89;Schumann等[10]利用水位实测数据校正LISFLOOD-FP SGC模型和VIC模型并预测Zambezi河下游地区的洪水淹没情况,预测精度达到2个像素以内;谢五三等[11]利用FloodArea模型耦合39个站点的水文监测数据完成大通河流域的淹没模拟及检验工作,模拟结果与实测值较为吻合。尽管上述模型在当地洪涝预警方面成果显著,但这些模型的使用大都集中在拥有密集水文站点和丰富实测数据的干流水系,其共同点是都需要水文实测数据的支撑。而由于水文监测的人力、设备成本巨大,大部分支流水系,尤其是广大发展中国家或者欠发达地区的中小流域缺乏必要的水文监测站点,这些行之有效的洪涝灾害预警方法难以得到应用[12-13]。因此,迫切需要探索一种能够不依赖传统实测数据的洪涝灾害预警模型方法,与基于地面实测水文数据的洪涝灾害预警模型方法互为补充。
作为实测数据匮乏情况下的有效数据源,遥感卫星可以获取不同空间尺度的地表信息,且遥感技术具有反馈信息快、监测范围大、数据获取频次高等特征,能够准确、快速、密集地监测地面洪水的动态致灾过程,为实测数据匮乏的流域水系提供获取水文数据的可能[13-15]。近年来,合成孔径雷达(synthetic aperture radar, SAR)影像因具备全天时、全天候,且不受云雾天气干扰等优点,在水体范围提取[16-17]、水位信息反演[13, 18]等研究中发挥着重要作用。作为水文实测数据匮乏情况下的有效替代,SAR影像反演出的洪峰水位数据能否有效反映上下游水位间的动态响应规律,能否建立起基于上下游水位响应规律的洪涝预测模型,并在洪涝最大淹没范围预测工作中发挥作用,值得进一步研究。此外,作为洪涝灾害预警工作中的重要基础数据,数字高程模型(digital elevation model, DEM)数据对水位提取精度的影响较大。目前全球范围内应用较为广泛,精度较高的2种开源DEM数据(SRTM1数据和ASTER GDEMV2数据),由于产生机理不同,其洪峰水位反演结果和所建预测模型可能存在一定差异,因此在具体应用时也需要开展对比研究。综上,探索能否完全利用遥感技术,提取河段上下游洪峰水位信息,建立基于上下游水位响应规律的洪涝预测方法,进而实现以往基于实测台站数据才能开展的洪涝灾害预警工作,对中小流域水文实测数据匮乏地区的洪涝预警和备灾救灾工作具有重要意义。
作为“一带一路”沿线的重要节点国家,斯里兰卡地处亚洲南部,属热带季风气候,降雨频繁,洪涝灾害季节特征显著。位于斯里兰卡南部的Nilwara河流域无大型水利工程,且缺乏水文实测数据,每逢雨季,该流域多条河段洪水灾害频发,严重威胁到当地居民的生命财产安全。由此,在无水文监测站点或实测水文数据的Nilwara流域,建立一种完全基于遥感技术的洪涝预报方法具有重要的推广价值。基于此,本文利用Sentinel-1A影像提取Nilwara流域某洪涝多发河段2015—2017年内14期洪涝事件的洪峰水位信息,建立该河段的下游洪峰水位预测模型,结合洪水填充算法预测河段两侧在不同洪峰水位下的最大淹没范围,并对预测结果进行精度评价。在此基础上,进一步阐述建立起来的洪涝预测模型是如何在洪涝预警知识普及程度不高的中小流域发挥作用的。本研究旨在为水文实测数据匮乏地区的洪涝预警工作探索出一种简单、廉价,且具有可操作性的实施方案,以期为遥感大数据背景下的水利应用提供有益借鉴。
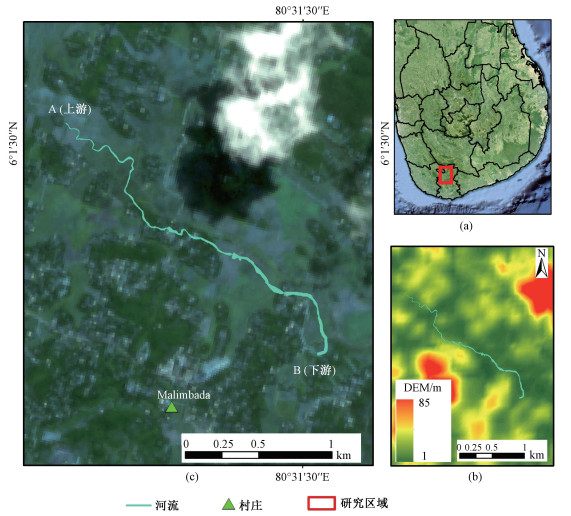
1 研究区与数据 1.1 研究区概况Nilwara流域位于斯里兰卡南部地区(图 1(a)),河流总长度78km,流域面积971km2,流域人口45.9万,每年6—8月,12月—次年2月,该流域多条河段表现出季节性洪水淹没,给当地居民造成严重的生命财产威胁。根据研究区实际情况,选取Nilwara流域洪水泛滥较为严重的河段开展本次实验研究(图 1(c))。该河段位于Nilwara流域的西南侧,长约3km,上游河道宽度约为10m,下游河道宽度约为30m,流经区域地势低平,周边土地覆盖类型以田地、林地为主(图 1(b))。
|
Download:
|
| 图 1 斯里兰卡Nilwara河研究区及地形高程 Fig. 1 Study area and local elevation in Nilwara Ganga, Sri Lanka | |
Sentinel-1A卫星IW模式下的Level-1级别地距影像数据(ground range detected,GRD)可以从Sentinel-1科学数据中心(https://scihub.esa.int)免费获取,该数据时间分辨率为12d,空间分辨率为5m×20m。利用欧空局发布的开源软件SNAP对Sentinel-1A卫星影像进行预处理工作,主要包括辐射校正、斑点噪声抑制、影像配准、几何校正等[19]。
全球降水测量(global precipitation measurement, GPM)数据可从NASA官网(https://pmm.nasa.gov/)获取,该数据的时间分辨率最高可达0.5h,主要提供研究区内多期洪涝事件发生时的最大雨强信息,以筛选出能够记录河段上下游洪峰淹没信息的Sentinel-1A影像。考虑到中小流域最大雨强的造峰时间较短(一般为几小时)[20],且斯里兰卡地区与Nilwara河类似河流的上下游洪峰传播时间为1~2d[21],Sentinel-1A影像的具体筛选原则为:1) 保留最大雨强出现1~2d后的最新一期Sentinel-1A影像作为记录洪峰淹没信息的有效数据; 2) Sentinel-1A影像的获取时间应尽可能接近下游洪峰到达时间,以保证影像的时效性(本文控制在6d以内)。通过以上原则,利用GPM数据对研究区2014—2018年雨季的54期Sentinel-1A影像进行筛选,并最终得到2015—2018年的18期洪涝事件的最大淹没影像(表 1)。
|
|
表 1 Sentinel-1A数据获取时间和数据类型 Table 1 Acquisition date and data type of Sentinel-1A images |
洪峰水位是指一次洪水过程中或者完整洪涝事件内某河道断面的最高水位值, 在不考虑外界影响的条件下,近似认为洪涝最大淹没范围由洪峰水位决定。由此,准确识别洪涝最大淹没范围是确定上下游洪峰水位的首要工作[4]。尽管目前已有多种淹没自动提取算法,如监督分类法、滤波法、灰度阈值分割算法[19]等,但在实际工作中,自动提取算法易受研究区地势地形和植被的干扰,在受淹植被区的提取精度与视觉解译法相比仍存在较大差距[16, 19]。为尽可能获取高精度的淹没提取结果,减少因提取精度造成的不确定性,本文采用目视解译的方法识别河段两侧最大淹没范围,识别精度控制在1~2个像素范围之内。具体识别原则如下[22]:1) 淹没区域的亮度与边缘形状与非淹没区域形成鲜明对比;2) 淹没区域与河道相互连接且大都平行于河道。
根据研究区的地势地形,该河段洪水演进过程可以近似视为一维洪水淹没过程[2]。在这种情况下,河道断面方向上的水面被近似认为处于同一水平高度,通过提取河道断面方向上被淹没栅格的最大高程并将其赋值给对应的河道断面来约束该断面的洪峰水位[23]。
| $ {Z_{洪峰水位}} = {\rm{Max}}\left( {{Z_1}, \cdots , {Z_n}} \right), $ | (1) |
式中:Z表示河道断面方向上被淹没栅格的高程值; n表示河道断面方向上被淹没的栅格数目; Max函数表示取所有值中的最大值。
2.2 相应水位法根据相应水位法相关原理,无支流河段的上下游洪峰水位关系[3]可以概括为
| $ {Z_{下, t + \pi }} = f\left( {{Z_{上, t}}} \right), $ | (2) |
式中:Z上,t表示t时刻上游的洪峰水位;Z下,t+π表示同一洪涝事件中t+π时刻下游的洪峰水位;f函数表示河段上下游洪峰水位间的映射关系,可以由多期上下游洪峰水位数据回归拟合获得。
2.3 洪水填充算法与传统种子填充算法只用单个点的水位信息(点型水位数据)约束淹没范围不同[24],本文利用整条河段自上而下逐渐降低的洪峰水位线(线型水位数据)约束沿河两侧的最大淹没范围。当给定河段上游洪峰水位时,下游洪峰水位可由下游洪峰水位预测模型(式(2))预测得出,上下游之间断面的洪峰水位可沿河道方向内插获得。对于一维洪水淹没过程,最大淹没范围获取的主要步骤如下:1) 将洪峰水位沿河道断面方向向两侧扩展, 高程低于对应洪峰水位的区域被初步判定为淹没区;2) 考虑有源淹没情况,删除无法与河道相互连接的淹没区[25]。水深信息可以通过洪峰水位减去对应栅格的DEM获得,计算公式[26]为
| $ D = Z - {E_{\rm{G}}}, $ | (3) |
式中:D表示研究区域洪水深度;Z表示研究区域洪水水位高度;EG表示研究区域地表高程。
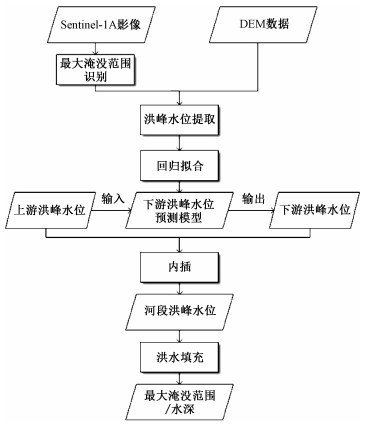
相关技术流程如图 2所示。
|
Download:
|
| 图 2 方法流程图 Fig. 2 Flowchart of method | |
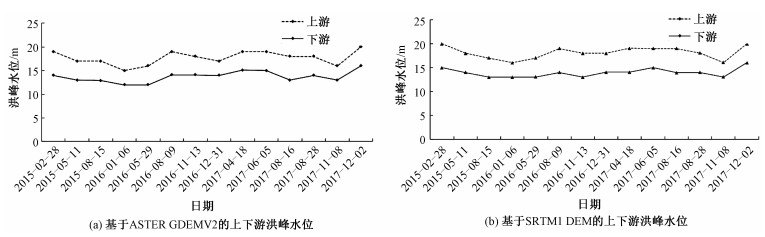
通过研究区2015—2017年Sentinel-1A卫星记录的14期洪涝事件的最大淹没影像,结合ASTER GDEMV2数据和SRTM1 DEM数据分别得到河段上下游的历史洪峰水位(图 3)。从上下游洪峰水位所处区间来看,ASTER GDEMV2数据下,上游地区历史洪峰水位最小值为15m,最大值为20m,洪峰水位抬升幅度为5m;下游地区历史洪峰水位最小值为12m,最大值为16m,洪峰水位抬升幅度为4m;SRTM1 DEM数据下,上游地区历史洪峰水位最小值为16m,最大值为20m,洪峰水位抬升幅度为4m;下游地区历史洪峰水位最小值为13m,最大值为16m,洪峰水位抬升幅度为3m。从河段上下游洪峰水位的对应关系来看,无论是ASTER GDEMV2反演出的洪峰水位数据还是SRTM1 DEM反演出的洪峰水位数据,上游洪峰水位到达下游后都有不同程度的降低,这体现了河水从上游传播到下游的过程中洪水传播能量逐渐减少,且地势逐渐降低,水位有所下降的现象。此外,洪峰在向下游传播的过程中,研究区河道宽度由10m变宽为30m左右,而下游洪峰水位的抬升幅度低于上游洪峰水位的抬升幅度,这说明自上而下河流宽度的逐渐增加对洪峰变化幅度起到了消减的作用,且上游洪水由于谷狭水急的特征,水位波动幅度大;下游谷底宽阔,水流平缓,水位波动幅度小。
|
Download:
|
| 图 3 基于ASTER GDEMV2和SRTM1 DEM的上下游洪峰水位提取结果 Fig. 3 The upstream and downstream flood peak levels derived from the ASTER GDEMV2 data and SRTM1 DEM, respectively | |
通过将多期上下游洪峰水位按照时间顺序进行排列,我们发现河段上下游洪峰水位间存在良好的响应关系,即在多期洪涝事件中,上游洪峰水位较前一期发生升高或者降低时,下游洪峰水位也会发生升高或者降低,对应具体洪涝事件的提取结果来看,ASTER GDEMV2数据和SRTM1 DEM数据下的水位反演结果差异不大。其中2017年6月5日—8月28日的3期洪涝事件的上下游洪峰水位在3年中处于较高水平,这与斯里兰卡2017年5—9月经历了特大洪涝事件相吻合。
3.2 模型构建及精度分析根据2015—2017年14期洪水事件提取出的上下游洪峰水位数据,通过回归分析的方法分别建立ASTER GDEMV2和SRTM1 DEM下的指数、线性、幂乘、二次项形式的下游洪峰水位预测模型。为进一步评估模型回归效果,选取R2和RMSE作为评价指标来评估模型的拟合优度和精度。
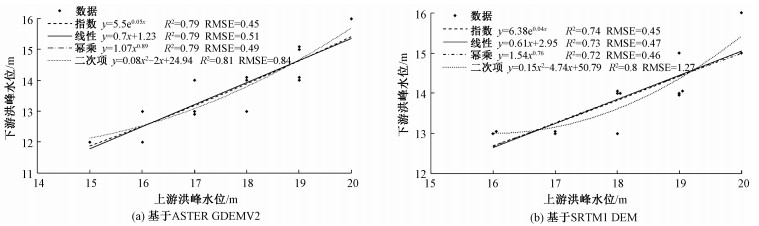
ASTER GDEMV2数据下,指数、线性、幂乘、二次项模型的R2分别为0.79,0.79,0.79和0.81,4种模型的RMSE分别为0.45,0.51,0.49和0.84(图 4(a)),由此可知该河段上下游洪峰水位之间存在较强相关性,4种预测模型拟合效果较好且相差不大。其中,二次项模型的可信度最优但RMSE值相对较大,表现出模型的不稳定性,其余3种回归模型的R2和RMSE相差不大。SRTM1 DEM数据下,指数、线性、幂乘、二次项模型的R2分别为0.74,0.73,0.72和0.80,RMSE分别为0.45,0.47,0.46和1.27(图 4(b))。其中二次项模型也表现出可信度略高但模型较不稳定的特点,其余3种模型的R2和RMSE相差不大。
|
Download:
|
| 图 4 基于ASTER GDEMV2和SRTM1 DEM的上下游洪峰水位回归关系 Fig. 4 Relationships between the upstream and downstream flood peak levels based on the ASTER GDEMV2 and SRTM1 DEM | |
通过对比2种DEM数据下所建模型的R2和RMSE,发现二者对应形式的预测模型拟合效果整体较为接近,其中ASTER GDEMV2数据下建立的预测模型整体效果略好一些,这可能与研究区特定的地势地形有关。综合二者洪峰水位反演结果差异不大的情况,说明以上2种DEM数据都可应用于Nilwara流域的水位提取及预测模型构建工作,这也印证了相关研究中SRTM1 DEM和ASTER GDEMV2数据在地势较为平缓的平原地区精度误差较为接近(二者平均误差皆不超过0.4m)的观点[27]。
基于以上分析,考虑到ASTER GDEMV2数据下建立的预测模型整体效果略好的情况,选取ASTER GDEMV2数据下模型回归可信度较高且RMSE相对较小、模型形式较为简单的指数模型作为该河段下游洪峰水位的预测模型
| $ y = 5.5{{\rm{e}}^{0.05x}}, $ | (4) |
式中:x表示研究区河段上游水位,m;y表示下游洪峰水位,m。
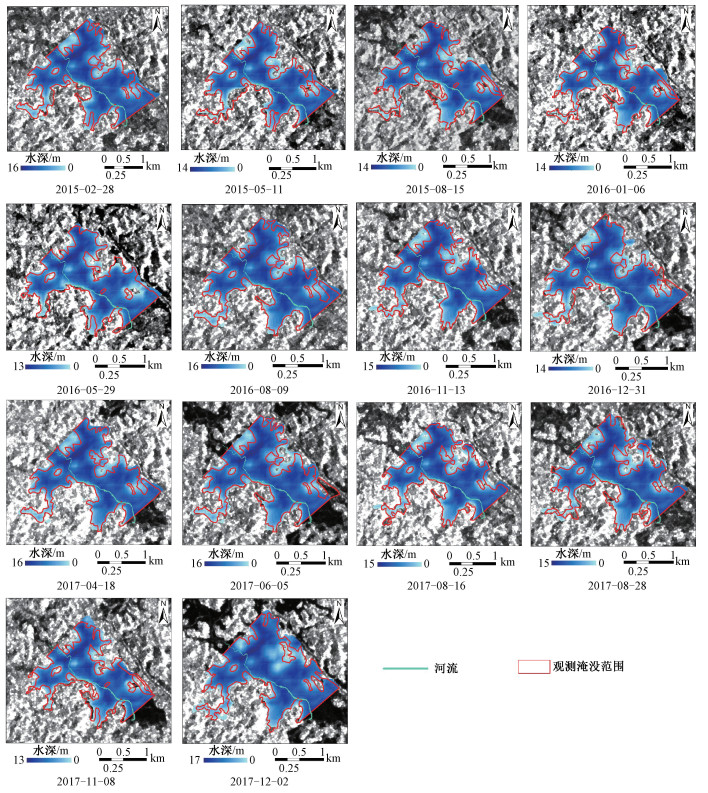
3.3 最大淹没范围预测根据下游洪峰水位预测模型,当给定上游洪峰水位时,可以预测得到河段下游的洪峰水位值。上下游之间河道断面的洪峰水位可通过线性内插获得。利用ASTER GDEMV2数据,根据2015—2017年14期洪涝事件的上下游洪峰水位分布情况,结合洪水填充算法及水深公式(式(3))得到14期洪涝事件的最大淹没范围及水深分布情况(图 5)。
|
Download:
|
| 图 5 最大淹没范围预测结果 Fig. 5 Prediction of the maximum flood extent | |
为准确评估预测精度,选取总体精度(overall accuracy, OA)作为评价指标来测定被正确预测的栅格数目占所有栅格数目的比例。预测结果和观测结果的标准混淆矩阵如表 2所示,其中N1为预测结果中属于淹没区域、观测结果中也属于淹没区域的栅格总数;N2为预测结果中属于淹没区域、但观测结果中属于非淹没区域的栅格总数;N3为预测结果中属于非淹没区域、但观测结果属于淹没区域的栅格总数;N4为预测结果属于非淹没区域、观测结果中也属于非淹没区域的栅格总数[22]。
|
|
表 2 预测淹没面积和观测淹没面积的混淆矩阵 Table 2 The confusion matrix of the predicted inundated area and the observed inundated area |
由于本文中研究区范围通过人为选择确定,当研究区范围过大时,N4的数值随之增大,会对总体精度造成较大程度上的高估。因此,本文移除了在预测结果中属于非淹没区域、在观测结果中也属于非淹没区域的栅格总数,新的总体精度[22]计算公式为
| $ {\rm{OA = }}\frac{{{N_1}}}{{{N_1} + {N_2} + {N_3}}}. $ | (5) |
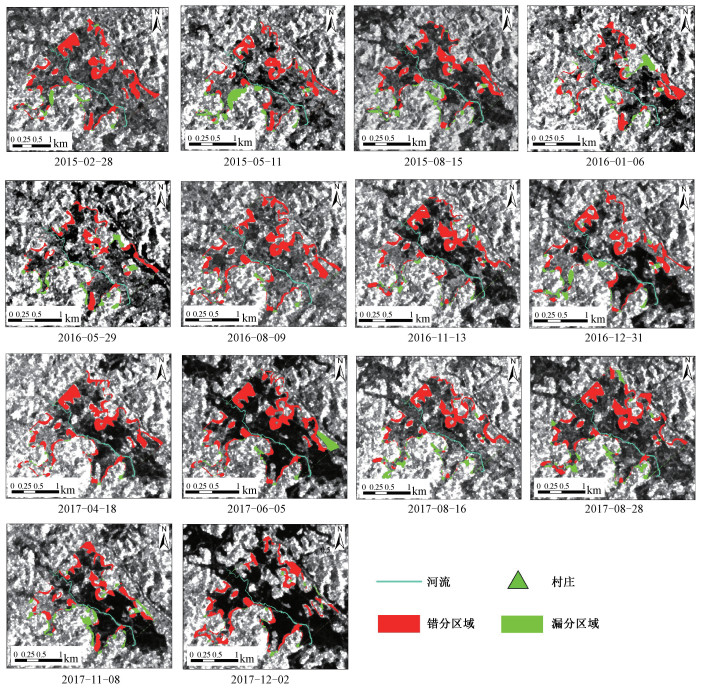
14期淹没预测结果中(表 3),总体精度最低为0.74,最高为0.81,平均值为0.76,显示出最大淹没预测范围与观测范围在空间位置上较好的一致性,实际淹没范围与预测淹没范围的差异分布如图 6所示。
|
|
表 3 最大淹没范围预测结果的总体精度 Table 3 The overall accuracy of the maximum flood extent prediction |
|
Download:
|
| 图 6 预测淹没范围与实际淹没范围的差异分布 Fig. 6 The difference distribution between the predicted and actual flood extent | |
通过建立的下游洪峰水位预测模型,结合洪水填充算法,可以在知道上游洪峰水位的情况下预测出下游地区的洪峰水位及最大淹没范围。如表 4所示,当研究区上游水位达到15m时,下游地区预测水位为11.90m,两侧最大淹没范围为3.56km2;当上游水位为20m时,下游预测水位可达15.38m,最大淹没范围为4.70km2。
|
|
表 4 下游洪峰水位及最大淹没范围预测结果 Table 4 The prediction of downstream flood peak levels and the maximum flood extent |
实际应用中,利用本文的技术方法可以在目标河段建立起适宜该河段的下游洪峰水位预测模型,并可将不同上游水位下的预测结果编制成上下游水位对应关系表的形式提供给河段周边潜在淹没区的居民。借助建立起来的上下游水位对应关系表,当上游水位到达一定高度时,上游社区居民可以通过电话等通信手段将上游水位情况及时告知下游社区管理者。下游社区管理者则可以利用编制的上下游水位对应关系表,迅速查阅出他们所在地区可能发生的洪水水位及最大淹没范围信息,并及时疏散潜在淹没区的居民,减少该地区的生命财产损失。
3.5 真实性检验为进一步验证2015—2017年14期遥感监测数据所建立的下游洪峰水位预测模型的准确性和可靠性,利用2018年4期洪涝事件提取出的洪峰水位数据进行了真实性检验。结果显示,4期下游洪峰水位预测结果(表 5)中,绝对误差最小值为0.20m,最大值为1.62m,平均值为0.83m,RMSE为1.01m,显示出下游洪峰水位预测模型具有较小的误差,模型稳定(根据DEM数据精度,表中上游、下游洪峰水位值保留到整数位)。
|
|
表 5 下游洪峰水位预测结果 Table 5 The prediction of downstream flood peak levels |
最大洪涝淹没范围预测中, 以上4期洪涝事件预测结果的总体精度分别为0.74,0.80,0.74和0.71。其中,最小值为0.71,最大为0.80,平均值为0.75,显示出预测结果较高的可信度。以上结果证明,利用遥感技术建立起的下游洪峰水位预测模型和洪水填充算法能够在给定上游洪峰水位的情况下较为真实、准确地预测该地区的下游洪峰水位和最大淹没情况,能够为当地的洪涝预警工作提供重要参考。
4 讨论已有不少学者将遥感反演出的河道水位数据应用于洪涝灾害研究当中,并就不同分辨率DEM的应用潜力开展了深入探讨[13]。如Schumann等[28]利用90m分辨率的SRTM DEM数据在地势平缓的Alzetee河地区开展水位提取及淹没模拟工作,其水位反演结果的RMSE为1.07m,淹没模拟精度为0.59,证明了粗分辨率DEM在平缓河漫滩地区的水位反演工作中具备一定潜力;Schumann等[2]和Matgen等[23]利用LIDAR获取的高精度DEM数据(2m)结合ENVISAT SAR影像开展洪涝研究工作,其洪峰水位反演的RMSE最高可达0.18m,淹没预测精度为0.74,显示出高精度DEM数据在洪涝灾害研究中的巨大价值。本文使用的是免费DEM数据,空间分辨率为30m,在目前无法获得研究区更高精度DEM的情况下,其洪峰水位反演的RMSE为1.01m,最大淹没范围预测的总体精度不低于0.71,基本能够满足与研究区类似的地势平缓地区的洪涝淹没精度要求。而在地形更加复杂情况下,基于立体像对方法可以生产5m,甚至2.5m、1m的DEM数据,在复杂地形的洪涝淹没预警技术研究方面具有较高的应用价值。未来工作中可在高精度DEM数据获取方面进一步开展研究,降低高精度DEM数据的获取难度,提升水文参数反演及洪涝淹没预测的准确性。
此外,在利用水文站点监测数据结合相应水位法进行洪峰水位预测方面,苏醒[3]在努尔敏河段开展了下游洪峰水位预测研究,其预测洪峰水位的RMSE可达0.21m;而傅太生等[5]则分别在镇江河段低潮位和高潮位的情况下建立了下游水文站的洪峰水位预测模型,其预测结果的平均误差小于0.10m。与以上研究相比,本文提出的方法在预测精度方面还存在一些差距,但在目前中小流域普遍缺乏实测数据的情况下,遥感反演出的洪峰水位数据可以在水文规律探索和下游洪峰水位预测方面发挥出高效的填补空白的作用,能够减少因水文实测数据不足对洪涝灾害预警工作造成的制约。
实际应用中,由于发展中国家和欠发达地区中小流域的居民一般缺乏洪水预警方面的专业知识,所以布置上下游水位对应关系表的方法是一种非常直观、廉价且具有操作性的洪水预警模式。目前,这一应用模式已经在斯里兰卡Kalutara地区的5个村庄得以应用[21],并起到了良好的预警效果(其中与Nilwara河类似的Kalu河的预警时间最长可达1~2d)。然而,该地区洪水预警表格的编制是当地学者实测当地地形,并利用该地区为数不多的水文监测数据结合HEC-RAS模型完成的,在其他缺乏水文监测数据的区域,洪水预警表格的编制仍存在较大难度。与之相比,本文提出的基于遥感技术的下游洪峰水位预测模型构建方法,可以在无水文实测数据的情况下在目标河段编制出类似的洪水预警表,进而为水文实测数据缺乏地区的洪涝预警工作提供帮助。
随着遥感大数据时代的到来,遥感数据的时间分辨率、空间分辨率、辐射分辨率、光谱分辨率不断提高,遥感数据类型不断丰富[29],为更加准确地预测洪水灾情提供了可能。下一步研究中,我们也将继续补充可用遥感数据,完善相关技术流程,进一步提升该方法的预测精度和可操作性。
5 总结与展望本文利用遥感技术,以Sentinel-1A SAR影像记录的研究区河段的多期洪峰淹没影像为数据源,提取河段上下游洪峰水位数据,揭示了上下游洪峰水位间的响应关系,通过建立的下游洪峰水位预测模型及洪水填充算法,对研究区内多期洪涝事件的最大淹没范围和水深分布信息进行计算。结果表明:
1) 基于遥感技术反演得到的洪峰水位数据能够较好地反映洪水动态致灾过程中的水文规律,较为准确地揭示了Nilwara河的上下游洪峰水位响应关系。
2) 基于遥感技术的下游洪峰水位预测模型和洪水填充算法能够有效预测Nilwara河的下游洪峰水位和两侧最大淹没范围,且预测结果总体精度较高(OA不低于0.71)。因此,该方法对水文数据缺乏地区的洪水预报工作有着重要的借鉴意义。
本文目前提出的方法更适用于类似Nilwara河这样无大型支流汇入、无水利工程扰动的干流河段。对于有支流汇入且存在人类水利工程干扰的河段,需要考虑支流及水利工程的同位相水位对干流洪峰水位的影响。在这种情况下,支流洪峰与干流洪峰到达汇流点时间可能存在较大差异,需要进一步研究洪峰传播时间对模型的影响。
| [1] |
赵阳, 程先富. 洪水灾害遥感监测研究综述[J]. 四川环境, 2012, 31(4): 106-109. Doi:10.3969/j.issn.1001-3644.2012.04.022 |
| [2] |
Schumann G, Hostache R, Puech C, et al. High-resolution 3-D flood information from radar imagery for flood hazard management[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(6): 1715-1725. Doi:10.1109/TGRS.2006.888103 |
| [3] |
苏醒. 相应水位法在努敏河洪水预报中的应用[J]. 黑龙江水利, 2016, 2(4): 20-23. Doi:10.3969/j.issn.1002-3305.2016.04.006 |
| [4] |
Hostache R, Matgen P, Schumann G, et al. Water level estimation and reduction of hydraulic model calibration uncertainties using satellite SAR images of floods[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(2): 431-441. Doi:10.1109/TGRS.2008.2008718 |
| [5] |
傅太生, 姚允龙, 陆益. 相应水位变化相关法预报长江干流感潮河段潮位的探讨[J]. 水文, 2007, 27(4): 56-58. Doi:10.3969/j.issn.1000-0852.2007.04.015 |
| [6] |
肖魁, 陈进. 长江宜昌-九江站间水流传播时间分析[J]. 中国农村水利水电, 2011(4): 1-5. |
| [7] |
祝中昊. 长江镇扬河段潮位预报相应水位法的改进[J]. 水文, 2000, 20(S1): 48-51. |
| [8] |
毛慧慧, 延耀兴, 张杰. 水文预报方法研究现状与展望[J]. 科技情报开发与经济, 2005, 15(19): 172-173. |
| [9] |
Matkan A, Shakiba A, Pourali S, et al. Flood early warning with integration of hydrologic and hydraulic models, RS and GIS (case study: Madarsoo basin, Iran)[J]. World Applied Sciences Journal, 2008, 6(12): 1698-1704. |
| [10] |
Schumann G J P, Neal J C, Voisin N, et al. A first large-scale flood inundation forecasting model[J]. Water Resources Research, 2013, 49(10): 6248-6257. Doi:10.1002/wrcr.20521 |
| [11] |
谢五三, 田红, 卢燕宇. 基于FloodArea模型的大通河流域暴雨洪涝灾害风险评估[J]. 暴雨灾害, 2015, 34(4): 384-387. Doi:10.3969/j.issn.1004-9045.2015.04.012 |
| [12] |
Schumann G J P, Bates P D, Neal J C, et al. Measuring and mapping flood processes[M]//Hydro-meteorological hazards, risks and disasters. Amsterdam: Elsevier, 2015: 35-64.
|
| [13] |
Grimaldi S, Li Y, Pauwels V R N, et al. Remote sensing-derived water extent and level to constrain hydraulic flood forecasting models: opportunities and challenges[J]. Surveys in Geophysics, 2016, 37(5): 977-1034. Doi:10.1007/s10712-016-9378-y |
| [14] |
Schumann G, Brakenridge G, Kettner A, et al. Assisting flood disaster response with earth observation data and products: a critical assessment[J]. Remote Sensing, 2018, 10(8): 1230-1248. Doi:10.3390/rs10081230 |
| [15] |
李加林, 曹罗丹, 浦瑞良. 洪涝灾害遥感监测评估研究综述[J]. 水利学报, 2014, 45(3): 253-260. |
| [16] |
孙亚勇, 黄诗峰, 李纪人, 等. Sentinel-1A SAR数据在缅甸伊洛瓦底江下游区洪水监测中的应用[J]. 遥感技术与应用, 2017, 32(2): 282-288. |
| [17] |
陈玲艳, 刘智, 张红. 基于水体散射特性的SAR图像水体检测[J]. 遥感技术与应用, 2014, 29(6): 963-969. |
| [18] |
Serpico S B, Dellepiane S, Boni G, et al. Information extraction from remote sensing images for flood monitoring and damage evaluation[J]. Proceedings of the IEEE, 2012, 100(10): 2946-2970. Doi:10.1109/JPROC.2012.2198030 |
| [19] |
周晗, 叶虎平, 魏显虎, 等. 基于Sentinel-1/2的水体提取方法对比研究: 以斯里兰卡小型水体为例[J]. 中国科学院大学学报, 2019, 36(6): 794-802. |
| [20] |
王兴斌, 缪韧, 赵瑜, 等. 改进美国法在中小流域设计洪水中的应用[J]. 水利科技与经济, 2013, 19(1): 20-22. Doi:10.3969/j.issn.1006-7175.2013.01.009 |
| [21] |
Nandalal K D W. Use of a hydrodynamic model to forecast floods of Kalu River in Sri Lanka[J]. Journal of Flood Risk Management, 2009, 2(3): 151-158. Doi:10.1111/j.1753-318X.2009.01032.x |
| [22] |
Renschler C S, Wang Z H. Multi-source data fusion and modeling to assess and communicate complex flood dynamics to support decision-making for downstream areas of dams: the 2011 hurricane irene and schoharie creek floods, NY[J]. International Journal of Applied Earth Observation and Geoinformation, 2017, 62: 157-173. Doi:10.1016/j.jag.2017.06.002 |
| [23] |
Matgen P, Schumann G, Henry J B, et al. Integration of SAR-derived river inundation areas, high-precision topographic data and a river flow model toward near real-time flood management[J]. International Journal of Applied Earth Observation and Geoinformation, 2007, 9(3): 247-263. Doi:10.1016/j.jag.2006.03.003 |
| [24] |
丁志雄, 李纪人, 李琳. 基于GIS格网模型的洪水淹没分析方法[J]. 水利学报, 2004, 35(6): 56-60, 67. Doi:10.3321/j.issn:0559-9350.2004.06.010 |
| [25] |
丁志雄, 叶梓川. 缺少水文资料的中小河流洪水风险计算模型与方法[J]. 中国防汛抗旱, 2012, 22(6): 54-57. |
| [26] |
易永红, 陈秀万, 吴欢. 基于遥感信息的淹没水深算法研究[J]. 地理与地理信息科学, 2005, 21(3): 26-29. Doi:10.3969/j.issn.1672-0504.2005.03.007 |
| [27] |
武文娇, 章诗芳, 赵尚民. SRTM1 DEM与ASTER GDEM V2数据的对比分析[J]. 地球信息科学学报, 2017, 19(8): 1108-1115. |
| [28] |
Schumann G, Matgen P, Cutler M E J, et al. Comparison of remotely sensed water stages from LiDAR, topographic contours and SRTM[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63(3): 283-296. Doi:10.1016/j.isprsjprs.2007.09.004 |
| [29] |
朱建章, 石强, 陈凤娥, 等. 遥感大数据研究现状与发展趋势[J]. 中国图象图形学报, 2016, 21(11): 1425-1439. Doi:10.11834/jig.20161102 |
 2022, Vol. 39
2022, Vol. 39 


