2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
无线传感器网络包含具有数据采集和通信功能的传感器节点[1], 节点由电池供电,但能量有限且难以有效补充。节点在传输数据时会消耗大量能量[2-3],数据传输的能耗会缩短整个网络的网络生存时间[4]。而数据融合技术可以提取传感器节点采集数据的特征,减少传输数据量,降低网络节点能耗,从而延长网络生存时间[5]。
如何增加数据可靠性、降低节点能耗及延长网络寿命是无线传感器网络数据融合算法的关键问题[6-7]。神经网络和无线传感网的相似性使其成为数据融合算法的研究重点[8-11]。文献[10]将BP神经网络用于环境监测场景中的多传感器数据融合,能降低监测数据维数。文献[11]提出基于BP神经网络的无线传感器网络数据融合算法(back-propagation networks data aggregation, BPNDA),算法以LEACH路由协议为基础,利用神经网络对簇成员采集的数据进行特征提取并汇聚数据至汇聚节点,有效地减少了数据传输通信量和节点传输能耗,但BP神经网络存在对初值敏感、易陷入局部最优解的问题。文献[12]提出一种基于改进蚁群和BP神经网络的数据融合算法,利用改进蚁群算法对BP神经网络进行优化,但只针对深井的场景。文献[13]提出基于事件驱动的动态分簇协议,并使用BPNDA算法进行数据融合,但事件驱动成本较高且未解决BP神经网络的缺陷。文献[14]提出基于遗传算法和粒子群算法优化BP神经网络的数据融合算法(GAPSOBP),算法结合分簇路由算法能有效减少数据传输量和节点能耗,延长网络生存时间。学者们为了解决数据融合算法中BP神经网络盲目选取初值、易陷入局部极值等问题,尝试将各类智能启发式算法与神经网络相结合。灰狼优化算法是一种新型的群体智能优化算法,算法在最优解方面已经被证明相较粒子群算法、遗传算法和其他智能启发式算法有更优的收敛速度和求解精度[15],但在实际应用时也会存在收敛性问题和局部极值问题[16]。
针对现有基于神经网络数据融合算法中网络非线性映射能力不足、数据特征提取不准确等问题,结合无线传感器网络实际传输情况,本文提出基于改进灰狼算法优化BP神经网络的无线传感器网络数据融合算法(improved grey wolf optimizer back-propagation networks data aggregation,IGWOBPDA)。文章主要分为3部分:1)提出基于正切函数的改进控制参数策略和动态权重位置更新策略来平衡灰狼算法局部与全局搜索能力; 2)提出IGWOBPDA算法模型。使用基于神经网络的数据融合模型,考虑到无线传感网实际传输节点能耗和分簇情况,为保证数据融合网络结构和网络负载的稳定性,提出基于节点剩余能量参数和节点密度参数的簇首选取方案,通过调整权重因子来适应网络数据融合传输过程中的实际情况; 3)提出IGWOBPDA算法流程。为解决数据融合中BP神经网络对初值敏感、易陷入局部最优解的问题,采用改进灰狼算法对BP神经网络初始阈值和初始权值进行优化,结合簇首选举方案,实现数据融合。IGWOBPDA算法不仅能提高数据融合精度,而且能均衡网络负载,降低网络数据传输量和节点传输能耗,从而延长网络生存时间。
1 改进灰狼优化算法 1.1 灰狼优化基本算法灰狼优化算法(grey wolf optimizer, GWO)[17]通过模仿灰狼种群在自然界的领导层级和群体狩猎方式来达到接近目标的目的。算法按适应度值将个体划分为4种等级层级:α、β、δ、ω。α为最优解,β、δ分别为第二、第三最优解,候选解为ω。算法数学模型[17]为
| $ \boldsymbol{D} = \left|\boldsymbol{C} \cdot \boldsymbol{X}_{p}(t)-\boldsymbol{X}(t)\right|, $ | (1) |
| $ \boldsymbol{X}(t+1) = \boldsymbol{X}_{p}(t)-\boldsymbol{A} \cdot \boldsymbol{D}. $ | (2) |
其中:D为灰狼个体与猎物间的距离向量; t为当前迭代次数; Xp(t) 为猎物的位置向量; X(t) 为灰狼个体位置向量; 收敛因子A=2a·r1-a,C=2·r2,r1、r2是[0, 1]的随机向量,a为控制参数。
灰狼种群有能力识别猎物的位置并包围。在数学抽象的搜索空间中,通过计算α、β、δ的位置向量来更新ω的位置向量[15]:
| $ \boldsymbol{D}_{\alpha} = \left|\boldsymbol{C}_{1} \cdot \boldsymbol{X}_{\alpha}-\boldsymbol{X}\right|, $ | (3) |
| $ \boldsymbol{D}_{\beta} = \left|\boldsymbol{C}_{2} \cdot \boldsymbol{X}_{\beta}-\boldsymbol{X}\right|, $ | (4) |
| $ \boldsymbol{D}_{\delta} = \left|\boldsymbol{C}_{3} \cdot \boldsymbol{X}_{\delta}-\boldsymbol{X}\right|. $ | (5) |
其中:X表示当前灰狼个体的位置; C1、C2、C3为随机扰动向量; Xα、Xβ、Xδ分别为α、β、δ的位置; Dα、Dβ、Dδ分别为α、β、δ与当前灰狼个体的距离。
| $ \boldsymbol{X}_{1} = \boldsymbol{X}_{\alpha}-\boldsymbol{A}_{1} \cdot \boldsymbol{D}_{\alpha}, $ | (6) |
| $ \boldsymbol{X}_{2} = \boldsymbol{X}_{\beta}-\boldsymbol{A}_{2} \cdot \boldsymbol{D}_{\beta}, $ | (7) |
| $ \\ \boldsymbol{X}_{3} = \boldsymbol{X}_{\delta}-\boldsymbol{A}_{3} \cdot \boldsymbol{D}_{\delta}, $ | (8) |
| $ \boldsymbol{X}(t+1) = \frac{\boldsymbol{X}_{1}+\boldsymbol{X}_{2}+\boldsymbol{X}_{3}}{3} . $ | (9) |
式(9)表示ω狼在本轮更新中的最终位置向量。
1.2 改进非线性控制参数GWO算法具有能自适应调整的收敛因子和控制参数机制。在式(2)中,a线性减小使得收敛因子A在[-a, a]区间内变化。当|A|>1时,狼群散开全局搜索; 当|A| < 1时,狼群集中靠近最优解。控制参数a影响着收敛因子A的收敛,进而影响狼群全局或者局部搜索。文献[15]采用控制参数为线性递减的公式:
| $ a = a_{\max }-\left(a_{\max }-a_{\min }\right) \cdot \frac{t}{t_{\max }}, $ | (10) |
其中:amax=2,amin=0,tmax为最大迭代次数。
控制参数a随t的增加从2到0线性减小,由于GWO实际寻优过程是复杂而非线性分布的,线性减小a并不能完全平衡全局最优和局部最优的搜索能力。因此本文针对算法收敛性提出基于正切函数的非线性控制参数策略,公式如下
| $ a = a_{\max }-\left(a_{\max }-a_{\min }\right) \times \tan \left(\frac{{\rm{ \mathsf{ π} }} \cdot t}{4 \cdot t_{\max }}\right) . $ | (11) |
改进后的控制参数a变为非线性的递减,相较线性递减策略,在算法开始时,a递减速率较小,增加了全局搜索能力,在算法后期,a递减速率较大,改善了算法局部寻优问题的收敛速率。
1.3 动态权重位置更新策略GWO算法在α、β、δ狼的带领下进行位置更新,但式(9)显示了α、β、δ的同等影响力,然而α、β、δ是具有不同特征且领导影响力不同的。本文结合文献[18-19]的动态权重更新策略,提出基于适应度值和步长欧氏距离的动态权重位置更新策略,公式如下
| $ W_{1} = \frac{\left|\boldsymbol{X}_{1}\right|}{\left|\boldsymbol{X}_{1}\right|+\left|\boldsymbol{X}_{2}\right|+\left|\boldsymbol{X}_{3}\right|}, $ | (12) |
| $ W_{2} = \frac{\left|\boldsymbol{X}_{2}\right|}{\left|\boldsymbol{X}_{1}\right|+\left|\boldsymbol{X}_{2}\right|+\left|\boldsymbol{X}_{3}\right|}, $ | (13) |
| $ W_{3} = \frac{\left|\boldsymbol{X}_{3}\right|}{\left|\boldsymbol{X}_{1}\right|+\left|\boldsymbol{X}_{2}\right|+\left|\boldsymbol{X}_{3}\right|}, $ | (14) |
| $ w_{\alpha} = \frac{f_{\alpha}}{f_{\alpha}+f_{\beta}+f_{\delta}}, $ | (15) |
| $ w_{\beta} = \frac{f_{\beta}}{f_{\alpha}+f_{\beta}+f_{\delta}}, $ | (16) |
| $ w_{\delta} = \frac{f_{\delta}}{f_{\alpha}+f_{\beta}+f_{\delta}}, $ | (17) |
| $ \boldsymbol{X}(t+1) = \frac{w_{\alpha} \cdot W_{1} \cdot \boldsymbol{X}_{1}+w_{\alpha} \cdot W_{2} \cdot \boldsymbol{X}_{2}+w_{\alpha} \cdot W_{3} \cdot \boldsymbol{X}_{3}}{3} . $ | (18) |
其中:fα、fβ、fδ为适应度值,W1、W2、W3分别为灰狼种群对α、β、δ的学习率。ω狼在每轮位置更新的最终公式为式(18)。通过适应度权重w和学习率W综合考虑,动态调整α、β、δ对更新个体的影响权重比例,更加凸显灰狼α、β、δ对灰狼种群个体的影响,能更好平衡算法的学习搜索能力。
2 IGWOBPDA算法模型无线传感器网络传感器节点的能耗问题和网络生存时间的改善是当前研究的重点。无线传感器网络数据融合技术主要分为3类:数据级融合,特征级融合和决策级融合。决策级融合技术通过多种监测手段根据特征级融合提取的数据特征对目标进行识别、判别和分类等操作获得最终的决策级融合结果。本文主要研究基于神经网络的决策级数据融合算法。
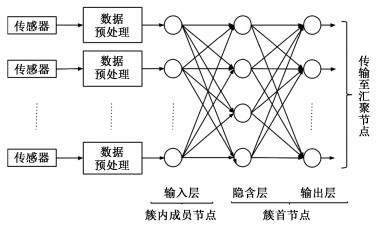
2.1 基于神经网络的数据融合模型无线传感器网络中LEACH算法提出在簇首节点进行数据融合的方式可以有效减少传输数据量,这使得在网络质量几乎未损失的情况下,网络只是增加了计算量而不增加通信能量[5]。本文以BPNDA算法为基础构建算法模型,利用LEACH算法的思想将网络划分成若干簇,每个簇结构作为BP神经网络模型。簇结构包括1个簇首节点和大量簇内节点:簇内成员节点进行数据监测,并预处理归一化数据; 簇首节点利用BP神经网络对数据进行特征提取,并将特征数据转发给汇聚节点。模型可减少传输数据量和能耗,延长网络生存时间。
图 1为算法模型。将3层BP神经网络应用至数据融合算法中,输入层设置于簇成员节点中,隐含层和输出层设置于簇首节点中。
|
Download:
|
| 图 1 IGWOBPDA算法模型 Fig. 1 Algorithm model based on IGWOBPDA | |
数据融合发生在簇首节点中,簇成员节点的监测数据的数据类型可能不同。为保证不同类型数据能够加权融合,簇成员节点对监测数据信息进行归一化预处理,并通过BP神经网络输入层将归一化结果发送至簇首节点。监测数据集xi(i=1, 2, …, n) 可以计算出数据均值和标准差
| $ \bar{x} = \frac{1}{n} \sum\nolimits_{i = 1}^{n} x_{i}, $ | (19) |
| $ e_{i} = \sqrt{\frac{1}{n} \sum\nolimits_{i = 1}^{n}\left(x_{i}-\bar{x}\right)^{2}} . $ | (20) |
其中: x、ei分别为数据均值和标准差。簇内成员节点将数据归一化后输出值为
| $ x_{i}^{\prime} = \left(x_{i}-\bar{x}\right) \cdot e_{i}. $ | (21) |
x′i将通过簇首节点的隐含层和输出层对传输数据进行融合处理。神经网络隐含层阈值值为Ri,γij为权值,bi为修正值,则输出层神经元功能函数为
| $ y_{i} = \sum\nolimits_{i = 1}^{n}\left(\gamma_{i j} R_{i}+b_{i}\right). $ | (22) |
簇首节点得到具有较小误差的簇内特征融合数据。网络神经元数据根据实际情况确定,由于能量、处理能力等限制,网络训练任务由汇聚节点完成。
2.2 改进分簇算法基于神经网络的数据融合模型以LEACH算法为基础。LEACH算法以概率的计算保证所有节点轮流当簇首,每个轮次节点会产生随机值φ(0 < φ < 1),若φ < T(n),则节点当选簇首。T(n) 计算公式[20]为
| $ T(n) = \begin{cases}\frac{p}{1-p \cdot\left(r \bmod \frac{1}{p}\right)}, & n \in G, \\ 0, & n \notin G .\end{cases} $ | (23) |
其中:G为未当过簇首的节点集,r为循环次数,p为簇首占比重。然而,LEACH算法簇首随机选取,可能导致能量不足的节点当选簇首,或者簇内节点过少,从而导致簇BP神经网络结构不稳定。因此本文综合节点剩余能量参数和节点密度参数,对簇首选举方案进行改进,以均衡网络能量负载,保证网络结构稳定。
2.2.1 节点剩余能量参数LEACH算法网络节点初始能量相同,但随着网络传输的进行,簇首节点能耗较大,频繁当选簇首会导致节点耗能过大甚至提前死亡。因此选择簇首应考虑节点剩余能量[20]。定义节点剩余能量参数Er=Ep/E0,Ep为节点剩余能量,E0为节点初始能量。
2.2.2 节点密度参数为保证数据融合网络模型稳定性,需考虑网络节点密度参数。在实际网络监测环境中,节点随机散落在监测区域,簇首的选举方案应考虑该节点附近节点数量。定义附近节点为该节点最大通信范围内的其他节点[21],数据集合为
| $ \operatorname{Node}_{r} = \{n \mid d(m, n) \leqslant R, m \in N, n \in N\}. $ | (24) |
本文定义节点密度参数为最大通信范围R内的附近节点数量与标准簇节点数量比。计算公式如下
| $ R = \sqrt{\frac{s_{\text {mon }}}{N \cdot p \cdot {\rm{ \mathsf{ π} }}}} \text {, } $ | (25) |
| $ \rho_{r} = \frac{m . \text { Node}_{r}}{\frac{1}{p}-1} . $ | (26) |
其中:smon为监测面积,N为网络节点个数; m.Noder为节点m的附近节点个数,1/p-1表示标准簇中附近节点数量。
算法考虑节点剩余能量参数和节点密度参数,对簇首选举的阈值公式进行更新
| $ \mathrm{T}(n) = \begin{cases}\frac{p}{1-p \cdot\left(r \bmod \frac{1}{p}\right)}\left(\alpha_{1} E_{r}+\alpha_{2} \rho_{r}\right), & n \in G, \\ 0, & n \notin G.\end{cases} $ | (27) |
其中:αi(i=1, 2) 为权重因子,满足α1+α2=1。当Ep很小时,Er会减小T的值,当前节点需要随机值φ比之前轮次更小才能当选簇首,式(27)能降低Ep较小的节点当选簇首的概率; 当节点位置不佳或附近节点数量过少,可能无法形成有效的网络结构进行数据融合,式(27)能降低ρr较小的节点T值。由此保证数据融合中网络的负载均衡。
权重因子可根据实际场景和网络结构调整。在网络运行初期,节点初始能量充足,α1可相对降低,在网络运行中后期,节点Ep降低,可增加α1值; 对于节点非均匀分布的场景,可适当增加α2值以保证网络结构稳定; 在节点均匀分部场景中,α2=0,但非实际情况可达到。
本文使用Matlab进行多次实验验证,在节点随机分布的场景中,一般情况节点密度参数权重α2≤1/4; 在多次实验验证中,考虑网络运行中节点能量的变化和网络节点随机密度,以保证数据融合传输的稳定性。本文设计在网络运行初期,节点能量充足,节点剩余能量参数权重α1=3/4,节点密度参数权重α2=1/4; 当节点剩余能量Ep≤40%E0,节点剩余能量参数权重α1=4/5,节点密度参数权重α2=1/5。
3 IGWOBPDA算法实现 3.1 IGWOBPDA算法流程IGWOBPDA算法利用改进分簇算法得到相对稳定的簇网络结构,汇聚节点采用与网络节点匹配的数据进行样本训练,并将训练得到的改进神经网络参数传输给对应簇首,簇首采用训练好的神经网络结构进行数据融合。具体算法步骤如下:
Step1 初始部署网络节点并上报节点信息。
Step2 设置网络节点权重因子α1=3/4,α2=1/4。
Step3 计算节点Er,由式(25)、式(26)计算节点ρr,由式(29)计算T(n)。网络确定簇首,形成稳定的簇结构。
Step4 簇首节点传输簇信息至汇聚节点等待训练。
Step5 汇聚节点按照簇信息确定BP神经网络结构,选取数据库数据集,使用IGWO算法优化BP神经网络初值,训练确定最优参数并存储。
Step6 汇聚节点发送训练最优参数至对应簇首节点。簇首节点确定簇内神经网络参数,进行数据融合并传输至汇聚节点。
Step7 若超过一半节点Ep≤40%E0,调整节点权重因子:α1=4/5,α2=1/5。返回Step3直到网络死亡。
其中,Step5采用IGWO(improved GWO)算法对BP神经网络的初始权值和阈值进行优化。BP神经网络算法模型初始权值和阈值选取具有随机性,经训练后可能达到局部最优而非全局最优,其精确度难以达到实际需求。初值的随机化会导致BP神经网络的样本训练随机化,网络训练结果震荡较大,陷入局部最优解。将BP神经网络初值优化问题转化为灰狼个体寻找猎物位置问题,提供给网络一个“足够好”的初值能有效提高网络非线性处理能力。
IGWO算法优化BP神经网络具体步骤如下:
Step1 设置搜索空间维度:d=M·N+N·1+N+1 (神经网络结构:M-N-1);BP神经网络参数向量
| $ \begin{gathered} \boldsymbol{U} = \left[\omega_{11}, \omega_{12}, \cdots, \omega_{1 N}, \cdots, \omega_{M 1}, \omega_{M 2}, \cdots,\right. \\ \left.\omega_{M N}, R_{1}, R_{2}, \cdots, R_{N}, \gamma_{1}, \gamma_{2}, \cdots, \gamma_{N}, \theta\right]. \end{gathered} $ | (28) |
其中:ωij(i∈[1, M], j∈[1, N]) 为神经元与隐含层权值,θ为输出层阈值; 设置种群规模n,最大迭代次数tmax和参数a、A、C。
Step2 初始化灰狼个体位置向量Xi(i=1, …, n)=U,Xi(i=1, …, n)∈[lb, ub]。
Step3 计算灰狼个体的适应度值:
Step4 排序灰狼个体位置信息{f(Xi),Xi},取前3灰狼个体设置为:Xα,Xβ,Xδ。
Step5 由式(3)~式(5)计算Dα、Dβ、Dδ; 由式(6)~式(8)计算X1、X2、X3; 更新A、C;
Step6 由式(11)更新a; 由式(18)更新Xi(t+1)。
Step7 更新f(Xi)、Xα、Xβ、Xδ。
Step8 若t≤tmax,或f(Xi) 达到预期目标,转至Step9;否则转至Step4。
Step9 记录Xα作为最优解Xbest,记Xbest=(Xbest1, Xbest2, …, Xbestd)=Ubest,用Ubest进一步训练。
3.2 算法复杂性分析在一次数据融合传输中IGWO算法与BP神经网络的训练为串行关系。设IGWO算法灰狼个体数为n,个体迭代时间为T,算法迭代m次,则运行IGWO算法时间复杂度为O(mn); BP神经网络结构为n1-n2-n3,则运行时间为(n1·n2+n2·n3)·T,时间复杂度为O(n2)。因此,IGWOBPDA算法时间复杂度为O(mn)+O(n2)。与节点传输能耗相比,CPU指令消耗的能量会更低,用较高的计算量换取较低的数据传输量有重大意义[3]。
4 仿真结果及分析本文使用Matlab2018a进行仿真实验。以环境监测场景作为应用场景,通过与BPNDA算法、GAPSOBP算法进行比较,从数据融合误差、算法收敛性、汇聚节点接收数据量、网络节点能耗、网络生存时间五个方面对IGWOBPDA数据融合算法进行仿真分析。
无线传感器网络仿真参数如表 1所示。设汇聚节点在网络部署外且位置固定,且有无限计算能力和能量,簇参数的训练更新过程都在汇聚节点完成。数据传输中的能耗计算采用文献[22]中的一阶无线电模型。
|
|
表 1 无线传感器网络仿真参数设置 Table 1 Simulation parameters of wireless sensor network |
1) 算法数据融合误差
本文采用UCI数据集的葡萄牙东北部地区森林火灾数据集(FFDS)。输入参数为4项森林监测数据,输出参数为森林烧毁面积(hm2)。确定BP神经网络隐含层节点的个数k使用“试算法”[18]:
实验数据融合误差采用3项指标进行对比,分别是平均均方误差(average relative error, AvRE)、均方根误差(root mean squared error, RMSE)、拟合优度(goodness of fit, R2),计算公式为
| $ \operatorname{AvRE} = \frac{\sum\nolimits_{i = 1}^{n}\left|y_{i}^{\prime}-y_{i}\right|}{n}, i = 1,2, \cdots, n, $ | (29) |
| $ \mathrm{RMSE} = \sqrt{\frac{1}{n} \sum\nolimits_{i = 1}^{n}\left(y_{i}^{\prime}-y_{i}\right)^{2}}, i = 1,2, \cdots, n, $ | (30) |
| $ R^{2} = \frac{\sum\nolimits_{i = 1}^{n}\left(y_{i}^{\prime}-\bar{y}\right)^{2}}{\sum\nolimits_{i = 1}^{n}\left(y_{i}-\bar{y}\right)^{2}}, i = 1,2, \cdots, n . $ | (31) |
其中: y′i为实验数据融合值,yi为实验数据预期值,y为实验数据预期值的平均值,n为实验数据数量。
表 2为BPNDA算法、GAPSOBP算法和IGWOBPDA算法的数据融合误差值。IGWOBPDA算法在3项误差指标中有明显的优势。其中,IGWOBPDA算法在AvRE指标上比BPNDA算法减少42.3%,比GAPAOBP算法减少8.7%;IGWOBPDA算法在RMSE指标上比GAPAOBP算法减少7.2%。
|
|
表 2 算法数据融合误差值 Table 2 The data fusion errors of algorithms |
为验证算法在不同数据集下的性能,本文选取另2个UCI数据集:巴塞罗那城市污水处理工厂的测量数据集(WTPDS)和葡萄牙葡萄酒检测数据集(WDS),融合误差(RMSE)结果如表 3所示。可以看出在不同数据集下IGWOBPDA算法融合误差值最低。算法提高了神经网络的非线性处理能力,有更好的数据融合准确性。
|
|
表 3 3种数据集下数据融合误差值(RMSE) Table 3 The data fusion error of three algorithms |
2) 算法收敛性
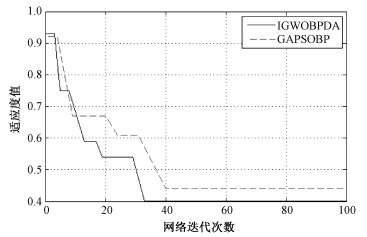
图 2为算法收敛性对比。IGWOBPDA算法和GAPSOBP算法随迭代次数不断地接近最优适应度值。IGWOBPDA算法大约在33代后就收敛至最优适应度值。表明了IGWOBPDA算法在使用自适应调整的控制参数和动态位置权重等可以较好的扩大寻优空间,有效避免局部最优解并提高算法收敛速度。
|
Download:
|
| 图 2 算法收敛性对比 Fig. 2 Comparison of the algorithms' convergence | |
3) 网络节点剩余能量
网络节点剩余能量是有效反映无线传感器网络网络效率的性能指标。由图 3可知,IGWOBPDA算法对网络的能耗速率明显低于LEACH算法和BPNDA算法。由于IGWOBPDA算法一方面考虑到节点能量参数和节点密度参数能更好的均衡网络能耗,另一方面能更有效的融合数据,减少网络数据传输量,降低节点能耗。随着网络规模的增加(n=100,n=150,n=200),IGWOBPDA算法节点平均能耗速率降低,能较好均衡网络能耗。

|
Download:
|
| 图 3 算法网络节点剩余能量对比 Fig. 3 Comparison of remaining energy of algorithm network nodes | |
4) 汇聚节点接收数据量
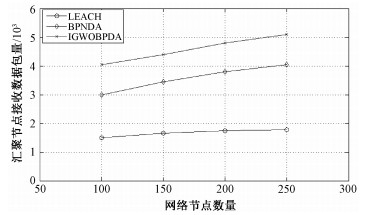
图 4为网络节点数在LEACH算法、BPNDA算法和IGWOBPDA算法下对汇聚节点接收数据量的影响。IGWOBPDA算法对汇聚节点接收数据量有明显提升。随着网络规模的增加,由于信道带宽等限制,LEACH算法接收数据量稳定,而IGWOBPDA算法接收数据量稳步提升。IGWOBPDA算法采用改进神经网络进行数据融合,能够更有效的融合数据和均衡网络负载,算法减少了网络数据通信量并消除网络拥塞,增加了汇聚节点接收到的有效数据包量,增加了数据的准确性和完备性。IGWOBPDA算法在已知大数据集的前提下,随着规模的增加,数据融合性能有一定优势。
|
Download:
|
| 图 4 不同网络规模下的数据量 Fig. 4 Amounts of packets at different network sizes | |
5) 网络生存时间
本文采用文献[23]对网络生存时间的定义,当传感器网络节点的存活率低于80%时,网络“死亡”,以保证网络可靠性。图 5中IGWOBPDA算法明显延长了网络生存时间。

|
Download:
|
| 图 5 算法网络网络生存时间对比 Fig. 5 Comparison of algorithms' network lifetime | |
为了优化无线传感器网络数据融合算法的数据可靠性、网络能耗等问题,且针对基于神经网络的无线传感器网络数据融合算法中对BP神经网络初始值敏感,考虑到无线传感器网络实际传输情况,本文提出基于改进灰狼算法优化BP神经网络的无线传感器网络数据融合算法IGWOBPDA。算法首先提出基于正切函数的控制参数和动态权重位置更新策略的灰狼算法改进方案,使用改进方案优化BP神经网络的初始权值和阈值,有效避免了BP神经网络初始值的随机性,提高网络非线性处理能力; 其次提出基于节点剩余能量和节点密度参数的成簇方案,通过调整参数权重来适应数据融合传输过程中的实际情况,保证了数据融合网络结构和负载的稳定性。仿真实验结果表明,该算法相较于BPNDA算法和GAPSOBP算法,在不同数据集下有更快的收敛速度,可至少减少7.2%的数据融合均方根误差,并且能减少网络能耗、降低数据传输量、延长网络生存时间,随着网络的规模增加保持稳定性。
| [1] |
Rawat P, Singh K D, Chaouchi H, et al. Wireless sensor networks: a survey on recent developments and potential synergies[J]. The Journal of supercomputing, 2014, 68(1): 1-48. Doi:10.1007/s11227-013-1021-9 |
| [2] |
Manshahia M S. Wireless sensor networks: a survey[J]. International Journal of Scientific&Engineering Research, 2016, 7(4): 710-716. |
| [3] |
Min R, Bhardwaj M, Cho S H, et al. Energy-centric enabling technologies for wireless sensor networks[J]. IEEE Wireless Communications, 2002, 9(4): 28. Doi:10.1109/MWC.2002.1028875 |
| [4] |
Bai X, Wang Z, Sheng L, et al. Reliable data fusion of hierarchical wireless sensor networks with asynchronous measurement for greenhouse monitoring[J]. IEEE Transactions on Control Systems Technology, 2019, 27(3): 1036-1046. Doi:10.1109/TCST.2018.2797920 |
| [5] |
Heinzelman W B, Chandrakasan A P, Balakrishnan H. An application-specific protocol architecture for wireless microsensor networks[J]. IEEE Transactions on Wireless Communications, 2002, 1(4): 660-670. Doi:10.1109/TWC.2002.804190 |
| [6] |
Boyinbode O, Le H, Mbogho A, et al. A survey on clustering algorithms for wireless sensor networks[C]//2010 13th International Conference on Network-based Information Systems. Takayama: IEEE, 2010: 358-364.
|
| [7] |
成瑜娟, 张敏洪. 感应半径可调的无线传感器网络生命周期的研究[J]. 中国科学院研究生院学报, 2011, 28(6): 768-775. Doi:10.7523/j.issn.2095-6134.2011.6.010 |
| [8] |
Heinzelman W R, Chandrakasan A, Balakrishnan H. Energy-efficient communication protocols for wireless microsensor networks[C]//Proceedings of 33rd Hawaii International Conference on System Sciences. Hawaii: IEEE, 2000: 8020-8030. DOI: 10.1109/HICSS.2000.926982.
|
| [9] |
孔玉静, 侯鑫, 华尔天, 等. 基于BP神经网络的无线传感器网络路由协议的研究[J]. 传感技术学报, 2013, 26(2): 246-251. Doi:10.3969/j.issn.1004-1699.2013.02.020 |
| [10] |
Sung W T. Employed BPN to multi-sensors data fusion for environment monitoring services[C]//Proceedings of the 6th International Conference on Autonomic and Trusted Computing, Berlin: Springer, 2009: 149-163.
|
| [11] |
孙凌逸, 黄先祥, 蔡伟, 等. 基于神经网络的无线传感器网络数据融合算法[J]. 传感技术学报, 2011, 24(1): 122-127. Doi:10.3969/j.issn.1004-1699.2011.01.025 |
| [12] |
余修武, 刘琴, 李向阳, 等. 基于改进蚁群的BP神经网络WSN数据融合算法[J]. 北京邮电大学学报, 2018, 41(4): 91-96. Doi:10.13190/j.jbupt.2017-262 |
| [13] |
侯鑫, 张东文, 钟鸣. 基于事件驱动和神经网络的无线传感器网络数据融合算法研究[J]. 传感技术学报, 2014, 27(1): 142-148. Doi:10.3969/j.issn.1004-1699.2014.01.026 |
| [14] |
胡强, 王海涛, 底楠, 等. 无线传感网中一种智能数据融合算法的实现及仿真分析[J]. 传感技术学报, 2018, 31(2): 283-288. Doi:10.3969/j.issn.1004-1699.2018.02.022 |
| [15] |
Mirjalili S. How effective is the Grey Wolf optimizer in training multi-layer perceptrons[J]. Applied Intelligence, 2015, 43(1): 150-161. Doi:10.1007/s10489-014-0645-7 |
| [16] |
Ragulskis M, Vainoras A, Smidtaite R, et al. The logistic map of matrices[J]. Discrete and Continuous Dynamical Systems, 2017, 16(3): 927-944. Doi:10.3934/dcdsb.2011.16.927 |
| [17] |
Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. Doi:10.1016/j.advengsoft.2013.12.007 |
| [18] |
Fouad A. A Hybrid grey wolf optimizer and genetic algorithm for minimizing potential energy function[J]. Memetic Computing, 2017, 9(9): 1-13. Doi:10.1007/s12293-017-0234-5 |
| [19] |
Rodríguez L, Castillo O, Soria J, et al. A fuzzy hierarchical operator in the grey wolf optimizer algorithm[J]. Applied Soft Computing, 2017, 57: 315-328. Doi:10.1016/j.asoc.2017.03.048 |
| [20] |
Wei C J, Yang J J, Zhang Z M. A distributed energy-efficient clustering routing protocol for wireless sensor networks[J]. Chinese Journal of Sensors and Actuators, 2013, 26(7): 1014-1018. Doi:10.3969/j.issn.1004-1699.2013.07.23 |
| [21] |
黄利晓, 王晖, 袁利永, 等. 基于能量均衡高效WSN的LEACH协议改进算法[J]. 通信学报, 2017, 38(Z2): 164-169. Doi:10.11959/j.issn.1000-436x.2017270 |
| [22] |
Jang S, Kim H Y, Kim N U, et al. Energy-efficient clustering scheme with concentric hierarchy[C]//IEEE International RF and Microwave Conference. Seremban: IEEE, 2011: 79-82. DOI: 10.1109/RFM.2011.6168700.
|
| [23] |
Ishizuka M, Aida M. Performance study of node placement in sensor network[C]//24th International Conference on Distributed Computing Systems. Hachioji: IEEE, 2004: 598-603. DOI: 10.1109/ICDCSW.2004.1284093.
|
 2022, Vol. 39
2022, Vol. 39 


