合成孔径雷达地面运动目标指示(synthetic aperture radar-ground moving target indicator, SAR-GMTI)是雷达领域一个比较重要的研究方向^[1-3]。由于拥有更多的自由度信息，多通道检测方法常在杂波抑制方面比单通道方法具有更好的性能，如偏置相位中心天线技术(displaced phase center antenna, DPCA)^[4]、空时自适应处理技术(space-time adaptive processing, STAP)^[5]等。然而，以上方法各有其局限性，如DPCA技术需要满足严格的系统条件; STAP需要较大的计算量，且在非均匀场景下会产生较大的协方差矩阵估计误差。

Yan等^[6-7]提出，利用鲁棒主成分分析方法(robust principal components analysis, RPCA)来实现多通道广域监视雷达系统(wide area surveillance, WAS)的运动目标提取。其基本原理是：雷达回波看作是地面杂波、运动目标、噪声3部分组成; 因为多个通道在相同时间内观察到的是同一场景，所以在通道相位补偿、图像配准后，所有通道的杂波信号可认为是近似一致的(通道杂波间仍然会有些轻微的差别但差别很小，可将它们归入噪声部分); 运动目标在场景中是稀疏分布的，并且因为运动的影响，通道间仍留有一定的相位差。由此性质，文献[7]将回波信号预处理后，得到一个联合多通道数据的新观测矩阵，而后利用低秩和(二维)稀疏矩阵分解中的经典模型RPCA，对新观测矩阵进行处理，提取出代表运动目标的稀疏矩阵。

为更好地适用广域监视下的地面运动目标指示(WAS-GMTI)，Li等^[8-9]提出结构化RPCA(structured RPCA，s-RPCA)、行-模值约束的RPCA(row-modulus RPCA，rm-RPCA)以及基于相位约束的RPCA模型的动目标提取方法，其中效果较好且应用性较强的是rm-RPCA。

SAR-GMTI与WAS-GMTI系统在检测原理上没有本质区别，仅是检测域不同，用于SAR-GMTI的数据需要转换到图像域，而WAS-GMTI主要在距离-多普勒域中完成。因此上述几种基于低秩和稀疏矩阵分解的动目标提取方法，也可应用到SAR-GMTI系统中。但在实际处理SAR卫星数据时发现，以上方法不能完全抑制强杂波，且对慢速目标的提取能力较差。具体分析后认为，以上方法均是通过简单的凸松弛来近似逼近矩阵的低秩或稀疏性要求，其中稀疏逼近误差较大，即场景内的强杂波会倾向增大运动目标的稀疏性，而慢速目标又易被忽略。此外，因多通道SAR数据的特殊性质，使得矩阵分解模型中的加权参数经验值在多通道SAR-GMTI系统下不再适用。而上述方法都仅是设置若干组实验，然后依据实验结果来粗略确定此加权参数的取值。此类方式效率较差，且不能针对不同的多通道SAR-GMTI系统下的观测矩阵实现自动调整。

为解决上述问题，本文提出一种新的基于低秩和一维稀疏矩阵分解的多通道SAR-GMTI方法，其中主要在目标提取环节，创新性设计一个自适应的加权参数，并针对分解精度问题提出一个适应性更好的矩阵分解模型，最后利用增广拉格朗日乘子法(augmented Lagrange method，ALM)^[10]进行求解。利用仿真数据和高分三号(Gaofen-3, GF-3)SAR卫星数据，证实了该方法在运动目标提取方面的有效性。

1 RPCA与多通道SAR-GMTI问题描述 1.1 RPCA问题描述

若利用低秩性与(二维)稀疏性，矩阵分解原是如下的双目标优化问题：

$ \min \limits_{\boldsymbol{L}, \boldsymbol{S}}\left(\operatorname{rank}(\boldsymbol{L}),\|\boldsymbol{S}\|_{0}\right) \text { s. t. } \boldsymbol{D} = \boldsymbol{L}+\boldsymbol{S}. $

(1)

式中: rank(·)表示取矩阵的秩，‖·‖₀表示矩阵l₀范数(矩阵非0元素个数)。进一步引入一个加权参数λ，将此问题转化为如下的单目标优化问题：

$ \min \limits_{\boldsymbol{L}, \boldsymbol{S}} \operatorname{rank}(\boldsymbol{L})+\lambda\|\boldsymbol{S}\|_{0} \text { s.t. } \boldsymbol{D} = \boldsymbol{L}+\boldsymbol{S}. $

(2)

该问题是一个NP难问题，可以利用范数逼近松弛为一个易于求解的凸优化问题：

$ \min \limits_{\boldsymbol{L}, \boldsymbol{S}}\|\boldsymbol{L}\|_{*}+\lambda\|\boldsymbol{S}\|_{1} \text { s.t. } \boldsymbol{D} = \boldsymbol{L}+\boldsymbol{S} . $

(3)

式中: ‖·‖_*表示矩阵的核范数，‖·‖₁表示矩阵l₁范数。式(3)也常被称为RPCA。

1.2 多通道SAR-GMTI问题描述

各通道的回波信号成像后，需进行通道校正^[11]与图像配准。然后，将多个通道的数据分别列矢量化(即矩阵各列依次堆叠，形成一个新列向量)，若按通道顺序重组在一起，就可得到一个新观测矩阵D。从组成成分来看，此观测矩阵可认为是由表示地面杂波的矩阵L、表示运动目标的矩阵S、表示噪声的矩阵N共3部分组成：

$ \boldsymbol{D} = \boldsymbol{L}+\boldsymbol{S}+\boldsymbol{N}, \text { s.t. }\|\boldsymbol{N}\|_{\mathrm{F}} \leqslant \delta, \boldsymbol{D}, \boldsymbol{L}, \boldsymbol{S} \in \mathbb{C}^{m \times n}. $

(4)

其中：n表示SAR-GMTI系统的通道数，m是场景内的像素点数(若场景大小表示为$\mathbb{C} $^x×y，则m=x·y); ‖·‖_F表示矩阵的Frobenius范数; δ是衡量数据中可能存在的噪声的参数，理论上可为任意正数。

矩阵L的任意一列表示的是对应通道的地面杂波，这些不同列之间的杂波分量应是近似一致的。理想情况下，矩阵L是一个沿列方向秩为1的低秩矩阵。在SAR-GMTI模式中，各个通道的观测时间间隔是相对较短的。短时间内，运动目标在相邻通道上的成像域位置是很难改变的。虽然运动目标在单个通道的场景下稀疏分布，但在新观测矩阵中，相同运动目标会分布到同一行。这意味着矩阵S是一个结构化行稀疏的矩阵，即只在列方向上保持稀疏性，除少数动目标所在的行向量，其余均为零向量。并且，S中相邻列向量之间还具有模值相等、相位保持差值的性质。

2 基于低秩和一维稀疏矩阵分解的多通道SAR-GMTI方法

本文在已有研究的基础上，针对多通道SAR重组矩阵中杂波分量的低秩性、运动目标分量的一维稀疏性，提出一种矩阵分解精度更高的动目标提取方法。

基于低秩和一维稀疏矩阵分解的多通道SAR-GMTI方法的整体操作流程如图 1所示。预处理后，计算本文设计的自适应加权参数，并利用新模型将一维稀疏矩阵S从观测矩阵D中分解出来。最后，把稀疏矩阵S重新写成通道矩阵形式，取通道校正时的参考通道作为最终的运动目标提取结果。此方法中最关键的目标提取步骤描述如下。

2.1 矩阵分解模型

经典的矩阵分解模型要求，稀疏矩阵在行和列方向上需同时满足稀疏性要求。rm-RPCA模型则针对结构化行稀疏分布特性进行改进，利用l_{1, 2}范数(‖·‖_{1, 2}表示)约束稀疏矩阵S，并对位于S非零行上的所有元素进行限制。

但理论上，结构化行稀疏约束应使用l_{0, 2}范数，即计算矩阵中非零行的个数。因为这个问题是非凸的，所以松弛化为l_{1, 2}范数，使矩阵的每一行向量的2-范数都是最小的，从而达到矩阵行稀疏的约束目的。但这种逼近是有误差的，即场景内较大强度的杂波会混入矩阵S中，增大矩阵的稀疏性，同样慢速运动目标也会被忽略，从而在提取过程中遗漏到低秩矩阵L中。此误差严重影响了低秩和稀疏矩阵分解在多通道SAR-GMTI系统上的应用效果。并且在观测矩阵D中，运动目标所在的少数行是不同于其余行的，这些行的存在往往也会破坏矩阵的低秩结构。

文献[12-13]提出基于低秩和块稀疏矩阵分解的RPCA，主要应用于某些列是离群值的检测。结合rm-RPCA模型，本文提出一种新的适用多通道SAR-GMTI系统的结构化行稀疏鲁棒主成分分析模型(structural row-sparse RPCA, SRS-RPCA)，来进一步加强杂波背景的低秩性和运动目标的一维稀疏性：

$ \begin{aligned} &\min \limits_{\boldsymbol{L}, \boldsymbol{S} \in \mathbb{C}^{m \times n}}\|\boldsymbol{L}\|_{*}+\kappa(1-\lambda)\left\| \boldsymbol{L}\right\|_{1,2}+\kappa \lambda\left\| \boldsymbol{S} \right\|_{1,2}, \\ &\text { s.t. }\|\boldsymbol{D}-\boldsymbol{L}-\boldsymbol{S}\|_{\mathrm{F}} \leqslant \delta,\left|\boldsymbol{S}_{i j}\right| = \left|\boldsymbol{S}_{i k}\right|, \\ &j, k \in\{1, \cdots, n\}, \forall i. \end{aligned} $

(5)

式(5)通过引入l_{1, 2}约束的低秩矩阵L，利用正则化参数κ、λ，促使低秩矩阵中对应运动目标所在位置的行是零向量。并通过对多个通道的信息整合来判断该行是否有运动目标，若有则整行提取，若没有则置0，以此提高目标提取的准确性，有助于提高慢速运动目标的提取能力以及强杂波的抑制能力。不同于RPCA在视频监控、人脸识别等方面的应用^[12]，SRS-RPCA模型可直接应用到复数矩阵。

2.2 模型算法

矩阵分解模型有多种数值求解方法，其中非精确ALM(inexact ALM, IALM)相对速度更快、矩阵分解精度更高，故本文采用IALM求解式(5)。设约束因子μ>0, 则式(5)的拉格朗日函数式定义为

$ \begin{aligned} &\mathcal{L}(\boldsymbol{L}, \boldsymbol{S}, \boldsymbol{Y} ; \mu) = \|\boldsymbol{L}\|{ }_{*}+\kappa(1-\lambda)\|\boldsymbol{L}\|_{1,2}+ \\ &\kappa \lambda\|\boldsymbol{S}\|_{1,2}+\langle\boldsymbol{Y}, \boldsymbol{D}-\boldsymbol{L}-\boldsymbol{S}\rangle+ \\ &\frac{\mu}{2}\|\boldsymbol{D}-\boldsymbol{L}-\boldsymbol{S}\|_{\mathrm{F}}^{2}, \text { s.t. }\|\boldsymbol{D}-\boldsymbol{L}-\boldsymbol{S}\|_{\mathrm{F}} \leqslant \delta, \\ &\left|\boldsymbol{S}_{i j}\right| = \left|\boldsymbol{S}_{i k}\right|, j, k \in\{1, \cdots, n\}, \forall i. \end{aligned} $

(6)

其中：Y表示拉格朗日乘子，〈·, ·〉代表内积操作。当X, Y∈ $\mathbb{C} $^m×n，〈X, Y〉=Re(tr(X^HY))，其中Re(·)和tr(·)分别表示取矩阵的实部、求矩阵的迹。

为了得到下一步低秩矩阵L^(k+1)的表达式，将S^(k)、Y^(k)、μ^(k)看作固定已知的量。则可将求解L的子问题等效为

$ \begin{gathered} \boldsymbol{L}^{(k+1)} = \underset{L \in \mathbb{C}^{m \times n}}{\operatorname{argmin}}\|\boldsymbol{L}\|_{*}+\kappa(1-\lambda)\|\boldsymbol{L}\|_{1,2}+ \\ \frac{\mu^{(k)}}{2} \cdot\left\|\boldsymbol{G^{L}}-\boldsymbol{L}\right\|_{\mathrm{F}}^{2} . \end{gathered} $

(7)

其中：k表示第k次迭代，G^L=D-S^(k)+Y^(k)/μ^(k)。事实上，方程(7)没有一个封闭解，所以采用文献[14]中单调算子分裂法进行求解，直至收敛得到最优的L。

利用同样的方式固定L^(k)、Y^(k)、μ^(k)，对求解S的子问题进一步化简，可得

$ \begin{aligned} &\boldsymbol{S}^{(k+1)} = \underset{\boldsymbol{S} \in \mathbb{C}^{m \times n}}{\operatorname{argmin}} \sum\limits_{i = 1}^{m}\left(\kappa \lambda\left\|\boldsymbol{S}_{i} .\right\|_{2}+\frac{\mu^{(k)}}{2} \cdot\right. \\ &\left.\left\|\boldsymbol{G}_{i}^{S}-\boldsymbol{S}_{i} .\right\|_{2}^{2}\right), \\ &\text { s.t. }\left|\boldsymbol{S}_{i j}\right| = \left|\boldsymbol{S}_{i k}\right|, j, k \in\{1, \cdots, n\}, \forall i . \end{aligned} $

(8)

其中：G^S=D-L^(k)+Y^(k)/μ^(k)。由此，式(8)转化为S_i·^(k+1)的优化问题。文献[8]给出了近似解，记为S_i·^(k+1)= $\mathcal{F} $_κλ/μ^(k)(G_i·^S)。在i=1, …, m范围内对S_i·^(k+1)循环求解，可得到式(8)最终解。

L^(k+1)和S^(k+1)求解完成后，下一步更新拉格朗日乘子Y^(k+1)和约束因子μ^(k+1)=max(ρμ^(k), μ_max)。当循环条件满足最大迭代次数或分解误差‖D-L^(k)-S^(k)‖_F小于10^-7时，结束循环并输出最终分解结果。

整体来看，虽然IALM方法的收敛速率难以理论分析，但大量数值实验表明，对于几何增长的μ^(k+1)，仍可认为其是近似线性收敛。算法内部的计算量主要集中在单调算子分裂法部分的奇异值分解(singular value decomposition，SVD)。为减少计算量，实际利用PROPACK软件包只取部分奇异值及其对应的奇异向量，而非计算完整的SVD。

2.3 设计加权参数

矩阵分解模型中的加权参数λ实际对收敛速度、目标提取结果都有一定影响。文献[7]中的蒙特卡罗实验证明：若λ选值过大，部分动目标分量无法被有效提取; 若λ选值过小，杂波或噪声分量会夹杂在稀疏矩阵中一同被提取出来。合适的λ可保证运动目标在被提取的同时，还不包含任何噪声与杂波分量。

矩阵分解模型，一般根据经验设为$\lambda = 1/\sqrt {\max \left( {m, n} \right)} $^[15]。在求解实际问题时，此经验值通常能获得较好的实验结果。在多通道SAR-GMTI系统应用中，通道数n≪m，则将此经验值直接写为$\lambda = 1/\sqrt m $。

事实上，输入矩阵D有以下观测特性：行列数相差极大; 各分量矩阵不是广泛定义的低秩或二维稀疏矩阵; 实际观测的场景很大，导致稀疏矩阵S的稀疏度非常高。基于此判断矩阵分解在多通道SAR-GMTI系统中的应用完全不同于常规情况，因此需要根据实际应用的先验知识进一步调整加权参数，以提高矩阵分解的准确度。

根据λ性质可知，随稀疏度提高，λ应适量提高以增强目标分量的提取。引入与矩阵S稀疏度相关的参数Δ，在经验值的基础上稍作调整，提出自适应加权参数

$ \lambda_{\mathrm{adp}} = \lambda \cdot \varDelta. $

(9)

矩阵S是以行向量的形式稀疏分布，因此矩阵S的稀疏度可近似等价为单个场景下运动目标分布矩阵的稀疏度。则通过DPCA技术获得运动目标检测的初步结果T后，根据文献[16]，矩阵S稀疏度的近似值计算如下

$ \operatorname{sparseness}(\boldsymbol{S}) \approx \frac{\sqrt{m}-\|\boldsymbol{T}\|_{1} /\|\boldsymbol{T}\|_{\mathrm{F}}}{\sqrt{m}-1}. $

(10)

稀疏度的取值范围是[0, 1]，当矩阵内只有一个非零元素时，稀疏度可达到最大值。

由(式10)可知，随观测场景的增大，稀疏度无限接近于1，且增长率逐渐减小。考虑场景大小的实际影响，研究发现在一定场景大小范围内固定λ取值可获得较好的结果，随场景的进一步增大λ值也需适量提高。因此进一步调整参数Δ为

$ \varDelta = \varphi\left[\frac{\sqrt{m}}{h}\right\rceil \cdot \operatorname{sparseness}(\boldsymbol{S}). $

(11)

式中：$\left\lceil \cdot \right\rceil $是向上取整的数学符号，φ和h分别为系数参数、常量参数。根据大量的实验数据，本研究中φ取值为1.5，h取值为500。虽然没有系统的方法来选择这些参数，但这些经验值对所有的实验数据都是有效的。根据多通道SAR-GMTI系统下观测矩阵的特性计算不同的λ_adp，相比固定的λ，通常可获得更好的目标提取结果。

3 实验与分析 3.1 仿真数据验证与分析

利用机载SAR典型参数(见表 1)，设置5个沿方位向接收回波的通道，建立合成孔径雷达成像仿真系统。为简单起见，雷达的斜视角设为0°。

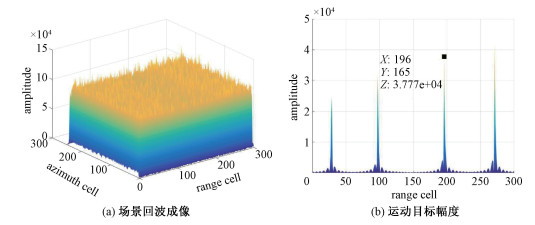
在方位向、距离向分别为250、300单元大小的场景下，布置4个运动目标，运动目标参数见表 2。由表可见，目标3的径向速度相对最慢。除运动目标外，还在场景的每个方位、距离单元上布置1个杂波点，并加入高斯分布的噪声。其中，杂波点的后向散射系数服从高斯分布，信噪比和信杂比分别设置为20 dB和-12 dB左右。图 2(a)给出了场景回波在距离-多普勒算法(range-Doppler，RD)成像后信号幅值的三维分布情况，可见运动目标完全淹没在杂波和噪声中。运动目标幅度如图 2(b)所示。

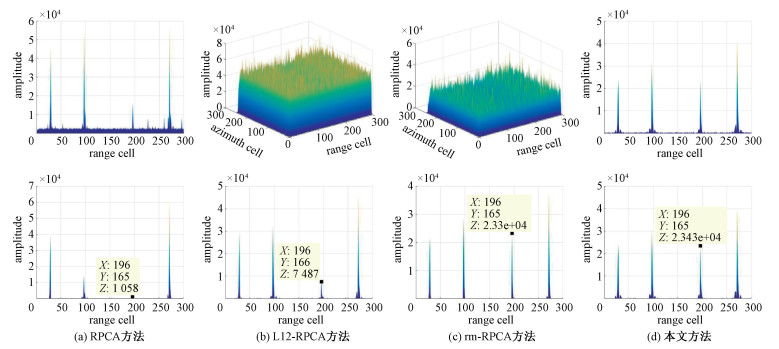
图 3表示的是在不同加权参数下，通过各矩阵分解模型得到的运动目标提取结果。每种方法的实验结果包含2行，其中第1行是在$\lambda = 1/\sqrt m $情况下得到的目标图像。如图 3的第1行图像所示，在RPCA方法得到的结果中，大量噪声与杂波混入运动目标被一同提取出来; L12-RPCA方法和rm-RPCA方法不能成功提取运动目标; 利用本文提出的SRS-RPCA模型得到的目标图像来看，提取结果仍是由少量噪声、杂波和动目标这3个成分组成，需要进一步利用恒虚警率处理来完成检测。基于图 3第1行图像的分析，认为加权因子经验值并不适用多通道SAR-GMTI系统应用。

若要准确提取运动目标且不包括任何杂波或噪声分量，则必须为各矩阵分解方法选择恰当的加权参数，实验结果如图 3中的第2行图像所示，其中基于SRS-RPCA模型方法选用的是自适应加权参数λ_adp。

为客观评价恰当加权参数下各矩阵分解方法的动目标提取效果，本文采用残差、幅度比值、迭代次数以及运行时间指标进行分析。残差指标是用来衡量各方法的运动目标提取结果与运动目标真实场景分布矩阵间的误差。若将运动目标成像后的信号分布矩阵表示为T，将实际检测结果表示为T^*，则残差定义为

$ \operatorname{Res} = \frac{\left\|\boldsymbol{T}-\boldsymbol{T}^{*}\right\|_{\mathrm{F}}}{\|\boldsymbol{T}\|_{\mathrm{F}}}. $

(12)

为细致观察具体某个运动目标的提取强度，本文引入幅度比值的概念。具体定义为，运动目标实际提取的幅值(t^*)与目标真实幅值(t)之间的比值：

$ \text { Ratio } = \frac{t^{*}}{t}. $

(13)

因为速度限制，慢速运动目标的信号强度相对表现较弱，地面运动目标检测方法对此类目标的检测能力也有一定局限性。为探究上述方法对慢速目标的检测效果，本文重点对慢速运动目标3的幅度比值参数进行分析，相关幅度信息已标注在图 2(b)、图 3中。针对图 3第2行图像的性能指标对比结果详见表 3。

基于残差数据指标分析可知，相比RPCA、L12-RPCA和rm-RPCA的目标提取方法，本文方法对场景内运动目标的提取结果更为准确。从慢速运动目标3的幅度比值参数来看，RPCA与L12-RPCA目标提取方法对慢速目标的提取效果相对较差，rm-RPCA目标提取方法与本文方法明显在慢速目标提取上更有优势。从迭代次数上看，本文方法收敛速度更快，而RPCA与L12-RPCA方法需单独处理矩阵的实数部分和虚数部分，实际迭代次数翻倍。在时间开销方面，本文方法通常比其他方法耗时更多，其额外的时间主要花费在单调算子迭代求解式(7)的过程。针对这个问题，本文将进一步寻找更优的数值求解算法。

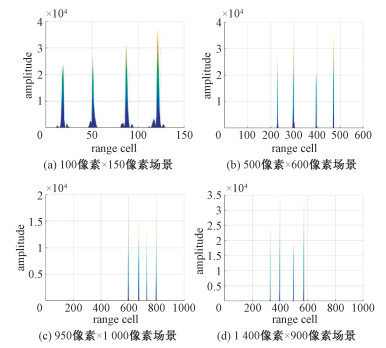
为进一步验证自适应加权参数的适用性，图 4比较了不同图像尺寸下，本文方法处理结果的对比，相关性能指标如表 4所示。主要考虑的是场景大小为100×150、250×300、500×600、950×1 000、1 400×900这5种情况，其余相关参数参考表 1与表 2。在所有场景中，加权参数均设置为自适应参数值λ_adp。由图 3(d)、图 4可知，运动目标均被准确提取且不包含任何杂波或噪声，此时运动目标提取残差也保持较小。表 4的最后2列给出了模型求解过程中的总迭代次数与总时间开销。正如第2.2节模型算法部分讨论的内容，数值求解需要基于多次迭代循环。在表 4中，迭代次数几乎保持恒定，说明无论场景多大，本文提出的方法总能以较快的速度进行收敛。

3.2 实测数据验证与分析

本节利用双通道的GF-3 SAR卫星数据，来验证本文方法在运动目标提取方面的有效性。GF-3卫星是中国首颗分辨率达到1 m的C频段SAR成像卫星。本文采用双通道GMTI试验模式的回波数据进行验证，原始图像如图 5(a)所示。图中运动目标因为速度的影响产生了位置偏移，如铁轨附近的一列火车、高速公路附近的一些车辆。从地面杂波来看，图 5(a)中铁轨的信号强度是远高于其他杂波的，也借此来考察本文方法对强杂波的抑制效果。

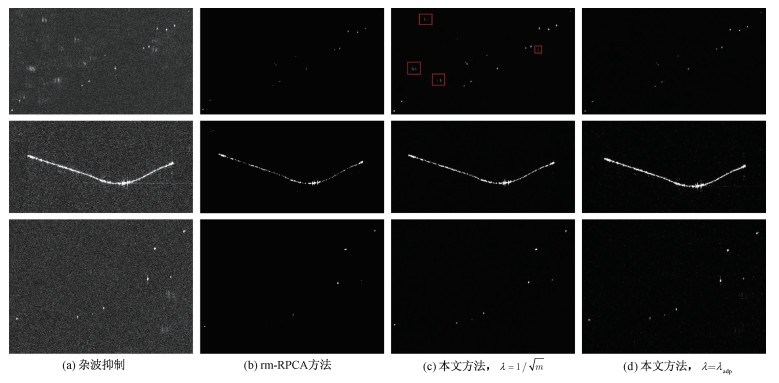
先采用一种常规的杂波抑制方法^[11]进行处理，结果见图 5(b)。图中除检测到的火车及部分汽车目标外，左上角还存在模糊现象，铁轨的抑制效果也不明显。为方便观察和比较动目标检测效果，将运动目标分布区域主要划分成3个部分：区域1、区域2、区域3。

接下来，分别采用rm-RPCA方法和本文方法对实测数据进行处理。为进一步验证自适应加权参数λ_adp的适用性，另设一组对比试验，即在采用本文提出的SRS-RPCA优化模型处理实验数据的基础上，将加权参数分别设为经验值$1/\sqrt m $和λ_adp。3个目标区域的处理结果如图 6所示，由上到下各行图像依次表示为区域1、区域2、区域3的目标提取结果。

从目标区域1的提取结果来看，对比杂波抑制效果，本文方法可对区域内的13个运动目标进行有效提取，rm-RPCA却只提取出12个运动目标。进一步比较，可知在$1/\sqrt m $取值下的本文方法处理结果中，部分模糊也随着运动目标一同被提取出来(如图 6(c)中红色矩形框标注所示)。由此证明，相比固定的经验参数$1/\sqrt m $，本文设计的λ_adp可使矩阵分解的效果更好。针对区域2内火车目标进行分析，认为其不同车身位置相对卫星的入射角是不一致的且不可忽略，从而导致不同位置车身目标的后向散射强弱不同，所以存在不同车身位置的目标提取能量不同的现象发生。由图可见，相比rm-RPCA模型方法，本文方法更能有效保留火车的能量。针对区域3，杂波抑制方法从中检测到8个有效目标，与本文方法检测结果保持一致，而rm-RPCA方法却只分解出6个目标。此结果说明，本文方法提取效果更好。

为观察强杂波的抑制效果，特取部分铁轨区域的处理结果进行放大，如图 7所示。通过比较可见，本文方法对强杂波的抑制作用更有效。

4 结论

基于多通道SAR-GMTI系统的数据特性，本文提出一种新的基于低秩和一维稀疏矩阵分解的多通道SAR-GMTI方法，主要根据GMTI特性设计了一个自适应的加权参数和新矩阵分解模型。基于仿真数据和GF-3 SAR卫星数据的实验结果证明，本文提出的方法在矩阵分解上更为准确，强杂波抑制和慢速运动目标提取方面的性能也得到进一步加强。