2. 中国科学院大学, 北京 100049;
3. 中国科学院无线传感网与通信重点实验室, 上海 200335
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Wireless Sensor Networks and Communications, Chinese Academy of Sciences, Shanghai 200335, China
无人机具有反应速度快、姿态变化多样等优点,搭载摄像头后,相比传统监控设备,监测范围更大,适用场景更广。基于无人机的对地目标跟踪在安防巡检、智慧交通等领域有很多落地应用,而对目标的逼近可以完成抵近侦察、精准打击等军事任务,因此成为当前的研究热点之一。
基于无人机的对地目标跟踪与逼近首先要估计目标位置,然后进行无人机控制,引导其完成目标任务。当前,主要使用目标跟踪算法检测目标在视频序列中的位置,以KCF(kernel correlation filter)[1]算法为代表的核相关滤波跟踪算法具有成功率高、速度快的优点,在工程中被广泛应用,但是目标跟踪过程中存在的目标尺度变化、目标遮挡问题仍是研究难点。
针对目标尺度变化问题,Li等[2]使用多个尺度因子,将检测区域进行不同程度的缩放,再使用线性插值的方式使目标图像调整到模板矩阵大小,然后使用相关滤波的方法分别求响应值,从中选择最优结果。DSST(discriminatiive scale space tracker)[3]算法利用三维滤波器、一维尺度、二维位置,先用位置滤波器计算目标的位置中心,然后使用尺度滤波器在33个尺度样本上估计最佳尺度。以上算法使用多个滤波器可以有效解决尺度变化问题,但也因此带来了算法的复杂性和冗余性,导致实时性降低。
针对目标遮挡问题,当目标在视野中重新出现时,LTD(tracking-learning-detection)[4]跟踪算法使用检测模块对图片帧进行全局搜索,重新定位目标位置,初始化跟踪模块,再次进行跟踪。张玉冰等[5]对目标进行分块,估计每个小块的位置,推算出目标的位置和范围,不仅增加了对遮挡的鲁棒性,同时解决了目标的形变问题。以上算法都可以解决目标的部分遮挡问题,但均不能保证实时性。
对于无人机的导引,文献[6]使用李亚普诺夫向量场法,将无人机的速度矢量和期望轨迹中的每个点相匹配,只要无人机按照匹配的速度飞行,便可以实现精确制导,但是寻找一个理想的Lyapunov函数是一大难点。文献[7]使用图像伺服控制器建立图像中目标运动与四旋翼运动之间的关系,通过求解Jacobian矩阵的伪逆,得到控制量,实现四旋翼的自主降落。对于具有欠驱动特性的四旋翼,需要对无人机建立复杂动力学模型。相比之下,比例导引法[8]用于无人机的控制,具有导引精度高、所需参数少、飞行轨迹平滑等优点,适合工程使用。
综合以上论述,考虑无人机与目标相对运动造成的目标尺度变化、部分遮挡等情况,提出改进的核相关滤波算法:首先将方向梯度直方图(histogram of oriented gradient, HOG)特征、Lab颜色特征和局部二值模式(local binary pattern, LBP)特征进行响应融合,提取检测区域的纹理信息,抑制边缘噪声; 然后根据无人机与目标的相对速度,计算自适应尺度因子,对目标图像缩放进行相关滤波检测; 最后判断峰值旁瓣比(peak sidelobe ratio, PSR)的值对模板进行自适应更新。根据改进KCF算法跟踪的结果,使用二维比例导引律控制多旋翼无人机运动,完成目标跟踪与逼近。
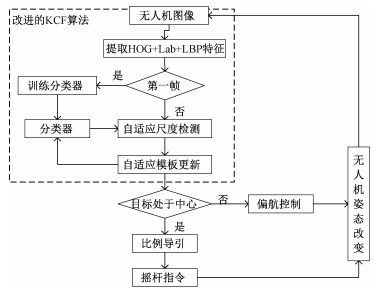
1 系统设计比例导引作用于无人机的速度方向,而带有半自主自驾仪的无人机可通过遥控指令,直接控制无人机的姿态。本文选用大疆Mavic Air-多旋翼无人机平台,带有三轴云台相机,利用其SDK(software development kit)开发地面站系统,获取无人机回传的图像。使用改进的KCF算法跟踪目标位置,比例导引负责解算速度指令,并通过虚拟遥杆控制无人机运动,其系统框如图 1所示。
|
Download:
|
| 图 1 系统框图 Fig. 1 The system block diagram | |
为增强目标跟踪算法对地面目标尺度变化、部分遮挡的鲁棒性,对KCF算法从特征融合、自适应尺度检测、自适应模板更新3个方面进行改进。地面站开发使用Android NDK,利用C++语言实现目标跟踪算法并在上层通过JNI(Java native interface)调用跟踪结果。无人机回传的图像首先经过改进的KCF算法,检测目标在视野中的位置。为了使用二维的比例导引,简化控制,需要根据目标位置控制无人机的偏航使目标处于视野的水平中心。当目标处于视野中心时,通过比例导引律计算无人机下一时刻需要的速度,大疆SDK提供了虚拟摇杆指令的接口,可直接向无人机发送速度指令,控制多旋翼姿态。
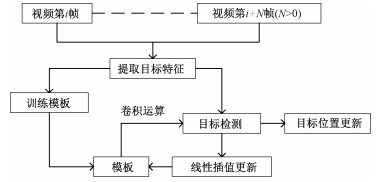
2 多旋翼无人机对地目标的KCF跟踪算法 2.1 KCF跟踪算法KCF跟踪算法是基于检测的跟踪,使用相关滤波器检测目标位置,然后不断学习、更新滤波器,提高鲁棒性。整个算法流程如图 2所示。
|
Download:
|
| 图 2 KCF算法流程 Fig. 2 The KCF algorithm flow | |
KCF算法主要分为3个步骤:1)初始化分类器:在视频序列中框选目标作为初始帧,利用循环矩阵稠密采样,构建正负样本,使用FHOG[9]和CIELAB提取目标HOG和Lab特征,训练模板矩阵作为分类器; 2)目标位置检测:对于后续帧,先提取待检测区域的目标特征,再求与候选区域的卷积响应,以响应值最大处作为目标的中心位置; 3)模板更新:以新的目标位置为基样本,使用循环矩阵重新采样,训练新的模板矩阵,为提高分类器鲁棒性,以线性插值的方式进行更新。
2.2 多旋翼无人机对地目标的KCF跟踪算法应用到无人机平台,本文主要从以下3个方面进行KCF算法改进。
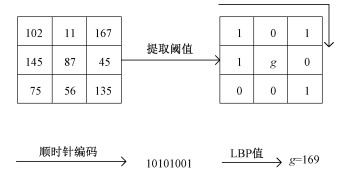
首先是特征融合。HOG特征提取目标的方向梯度直方图,可以很好地描述目标的轮廓,但是容易被边缘噪声干扰[10]。LBP算子提取图像的纹理特征,能够有效抑制噪声,本文将LBP特征串联在FHOG和Lab特征之后,形成3种特征融合的特征向量表示目标。如图 3所示,LBP算子即局部二值模式,通过阈值比较和编码形成LBP值,用以表示以当前像素为中心的邻域内的纹理信息。
|
Download:
|
| 图 3 LBP特征提取流程 Fig. 3 LBP feature extraction process | |
本文使用SEMB-LBP[11]特征,对LBP特征进行降维处理,同时保证信息的有效性。SEMB-LBP提取过程如下:
1) 将候选区域划分成若干个4×4大小的块,每个块划分成4个2像素×2像素大小的胞元,计算每个胞元的灰度平均值;
2) 将每个胞元作为一个整体,与邻域胞元进行比较,计算LBP值;
3) 对每个块中的LBP值求直方图并按bin值降序排列,将排序在前N位的bin值对应的LBP值作为样本SEMB_LBPs,重新对图像进行编码。特征图中(x, y) 处的LBP值L(x, y) 如果在样本库SEMB_LBPs中,则将其序号Index[L(x, y)] 赋值给L(x, y),如果不在样本库中,则令其等于N。例如,排序23的LBP值为127,编码后,所有LBP值为127的胞元,均被替换为23。取N=63,这样图像的灰度值范围变成0~63,共64种取值。公式如下
| $ L\left( {x, y} \right) = \left\{ {\begin{array}{*{20}{l}} {{\rm{Index}}\left[ {L\left( {x, y} \right)} \right], }&{L\left( {x, y} \right) \in {\rm{SEMB\_LBPs, }}}\\ {N, }&{其他.} \end{array}} \right. $ | (1) |
其次是自适应尺度。为解决目标跟踪过程中的尺度变化问题,SAMF[2]算法使用了尺度池方法,采用7个尺度,步长Si ={0.985, 0.99, 0.995, 1.0, 1.005, 1.01, 1.015},对每帧候选区域都进行Si倍的缩放,计算响应值。但是在计算大图像块时计算量很大,且7个尺度只有一个最终能用,造成冗余,不能保证实时性。
对于目标跟踪与逼近任务,目标在视野中的尺寸以正比于无人机和目标相对速度的速率增大。采用一种自适应的尺度因子,可以减小运算量,提高检测速度,如下所示
| $ L = 1 + V \times 0.01, $ | (2) |
其中:L为尺度因子,V为无人机与目标沿视线角方向的相对速度。
最后是失败检测与模板自适应更新,借用文献[12]使用PSR值进行跟踪失败检测的方法,设定PSR阈值,通过阈值比较检测跟踪是否失败。为避免在目标部分遮挡时学习到过多的背景信息,使用视频序列前10帧计算的PSR值的平均值的1/2作为阈值。如果此时的PSR值大于阈值,判定为跟踪成功,使用线性插值的方式,更新模板矩阵; 如果此时PSR值小于等于阈值,则跟踪失败,不进行模板的更新。
3 基于比例导引的多旋翼无人机跟踪与逼近 3.1 比例导引的基本原理比例导引律[13]可表示为
| $ {\eta _{\rm{c}}} = N{V_{\rm{c}}}\lambda ', $ | (3) |
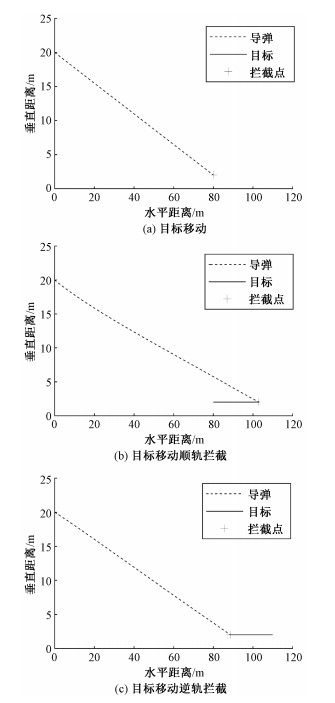
其中:ηc为导弹需要的加速度,N为常系数,Vc为相对速度,λ′为弹目线方向角变化率。图 4展示了无人机与目标的拦截曲线,假设无人机高度为20 m,图 4(a)目标静止,图 4(b)目标以0.5 m/s的速度前进,方向与无人机速度方向相同,图 4(c)目标以0.5 m/s的速度前进,方向与无人机速度方向相反。将速度矢量沿视线角方向分解为水平方向和竖直方向的速度,发送到无人机平台,便可以实现有效制导。
|
Download:
|
| 图 4 导弹与目标拦截曲线 Fig. 4 Missile and target interception curve | |
根据目标跟踪算法返回的结果,控制无人机的偏航,使目标在水平方向上处于视野中心,且相机俯仰角度为零。此时,将运动方程限制在竖直二维剖面内,通过求解无人机与目标的视线角变化率、相对速度就可以求得无人机的控制加速度。
如图 5所示:T为待跟踪的目标; 假设M点为机载相机的焦点,且与无人机重心重合,点B为成像平面的中心点,点A为T的投影点,此时处于成像平面水平方向的中线上,即直线AB为成像平面水平方向的中线。

|
Download:
|
| 图 5 无人机比例导引示意图 Fig. 5 Schematic diagram of drone proportional guidance | |
可根据无人机高度H、相机焦距f、视野中目标距视野中心的距离d,求得无人机与目标的视线角θ、无人机与目标的距离RTM,如下
| $ \theta = {\tan ^{ - 1}}\frac{d}{f}, $ | (4) |
| $ {\rm{RTM}} = H \times \frac{{\sqrt {{d^2} + {f^2}} }}{d}. $ | (5) |
对时间t求导即可得视线角变化率及相对速度:
| $ \frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = \frac{{d'f}}{{{d^2} + {f^2}}}. $ | (6) |
| $ \frac{{{\rm{dRTM}}}}{{{\rm{d}}t}} = {\rm{RTM}} \times \left[ {\frac{{H'}}{H} + \frac{{d \times d'}}{{{d^2} + {f^2}}} - \frac{{{d^{\prime 2}}}}{d}} \right]. $ | (7) |
其中:H′为无人机竖直方向的速度,d′为图像中目标在竖直方向的速度,设T为图像刷新的帧率:
| $ H' = \left( {{H_{T + 1}} - {H_T}} \right) \times T, $ | (8) |
| $ d' = \left( {{d_{T + 1}} - {d_T}} \right) \times T. $ | (9) |
UAV123数据集[14]是无人机拍摄的用于目标跟踪的数据集。为验证改进算法(GCF)的有效性,如表 1所示,在UAV123数据集中选取3个序列(bike1、person12、car18)与KCF算法、DAT[15]算法、STAPLE[16]算法进行对比实验,采用跟踪精度和成功率进行评估。
|
|
表 1 序列特点说明 Table 1 Sequence characteristics |
定义距离误差为算法估计的中心点(x1, y1) 与真实中心点(x2, y2) 的距离,表示如下
| $ {\rm{DS}} = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}.} $ | (10) |
设定阈值为20像素,则跟踪精度为误差距离小于20像素的帧数占所有帧的比例。
定义重合率为算法估计的目标框(记为a)与真实目标框(记为b)的比值
| $ {\rm{OS}} = \frac{{\left| {a \cap b} \right|}}{{\left| {a \cup b} \right|}}. $ | (11) |
假设当重合率大于α时,视为跟踪成功,成功率即为所有跟踪成功的帧占所有帧的比例。
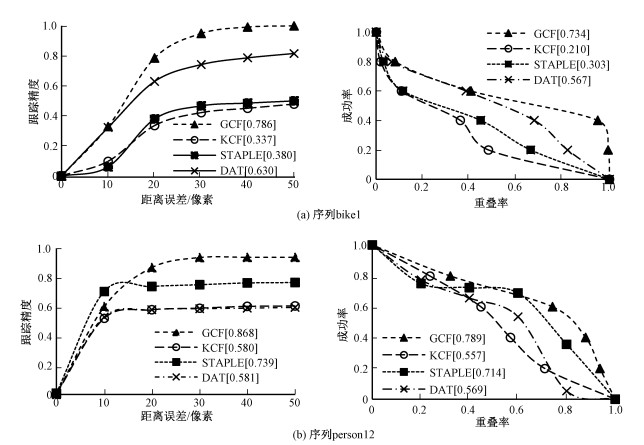
如图 6所示,由测试结果可知,对于改进的算法,设定距离误差阈值为20像素,跟踪精度能够稳定在0.6以上,设定重合率的阈值为0.5,成功率能够达到0.73以上。对比KCF算法,有效解决了目标部分遮挡、尺度变化等问题,提高了跟踪鲁棒性。对比其他算法,虽然算法性能提高不是很明显,但改进算法能保证实时性。
|
Download:
|
| 图 6 对比实验结果 Fig. 6 Comparative experimental results | |
图 7是算法改进前后的对比图,选自person12序列,第910帧,目标出现部分遮挡,此时原始算法仍在不断地学习、更新模板矩阵, 以至于学习到大量的背景信息,由于PSR值小于阈值,改进算法避免了背景的干扰。在第1 063帧,原始算法一直停留在目标被遮挡的地方,而改进的算法一直保持准确跟踪。

|
Download:
|
| 图 7 算法改进前后对比图 Fig. 7 Comparison before and after algorithm improvement | |
将改进的算法移植到地面站,进行外场实验,使用手势框选目标,如图 8所示,可以实现对目标的实时跟踪与逼近,并且能够自适应变化跟踪框尺度。

|
Download:
|
| 图 8 地面站实时记录画面 Fig. 8 Real-time recording screen of ground statio | |
经典KCF算法在目标跟踪问题上具有很强的实时性,但是不能很好地处理对地目标跟踪过程中的尺度变化、目标遮挡等问题。本文提出一种改进的KCF对地目标跟踪算法,以适用于无人机平台:1)提出融合的特征提取方法,在原有特征基础上叠加LBP特征,有效抑制边缘噪声; 2)结合无人机平台,设计了自适应的尺度因子,根据无人机与目标距离,实时调整目标在视野中的尺寸; 3)使用峰值旁瓣比,判断跟踪效果,对模板进行选择性更新。以跟踪精度和成功率两个方面与现有算法对比,证明了改进算法的有效性。最后基于Android平台,移植KCF算法,开发大疆四旋翼无人机的地面站,根据改进KCF算法的结果,采用比例导引的方法,完成目标的跟踪与逼近。
| [1] |
Henriques J F, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. Doi:10.1109/TPAMI.2014.2345390 |
| [2] |
Li Y, Zhu J K. A scale adaptive kernel correlation filter tracker with feature integration[C] //Computer Vision-ECCV 2014 Workshops, Springer, Cham, 2014: 254-265. DOI: 10.1007/978-3-319-16181-5_18.
|
| [3] |
Danelljan M, Häger G, Khan F S, et al. Discriminative scale space tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(8): 1561-1575. Doi:10.1109/TPAMI.2016.2609928 |
| [4] |
Kalal Z, Mikolajczyk K, Matas J. Tracking-learning-detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1409-1422. Doi:10.1109/TPAMI.2011.239 |
| [5] |
张玉冰, 罗青山, 曾贵华. 基于部件的对象实时跟踪[J]. 计算机工程与应用, 2008, 44(7): 69-69-71, 77. Doi:10.3778/j.issn.1002-8331.2008.07.020 |
| [6] |
Regina N, Zanzi M. 2D tracking and over-flight of a target by means of a non-linear guidance law for UAV[C]//2009 IEEE Aerospace conference. March 7-14, 2009, Big Sky, MT, USA. IEEE, 2009: 1-11. DOI: 10.1109/AERO.2009.4839606.
|
| [7] |
Lee D, Lim H, Kim H J, et al. Adaptive image-based visual servoing for an underactuated quadrotor system[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(4): 1335-1353. Doi:10.2514/1.52169 |
| [8] |
Ratnoo A, Ghose D. Impact angle constrained guidance against nonstationary nonmaneuvering targets[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 269-275. Doi:10.2514/1.45026 |
| [9] |
Felzenszwalb P F, Girshick R B, McAllester D, et al. Object detection with discriminatively trained part-based models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1627-1645. Doi:10.1109/TPAMI.2009.167 |
| [10] |
陈鹏展, 章新志. 基于TPLBP/HOG特征与DBN深度模型的人脸识别研究[J]. 测控技术, 2019, 38(6): 5-10. Doi:10.19708/j.ckjs.2019.06.002 |
| [11] |
Liao S C, Zhu X X, Lei Z, et al. Learning multi-scale block local binary patterns for face recognition [C]//International Conference on Biometrics. Springer, Berlin, Heidelberg, 2007, LNCS 4642: 828-837. DOI: 10.1007/978-3-540-74549-5_87.
|
| [12] |
Bolme D S, Beveridge J R, Draper B A, et al. Visual object tracking using adaptive correlation filters[C]//2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. June 13-18, 2010, San Francisco, CA, USA. IEEE, 2010: 2544-2550. DOI: 10.1109/CVPR.2010.5539960.
|
| [13] |
高晔, 周军, 郭建国, 等. 红外成像制导导弹分布式协同制导律研究[J]. 红外与激光工程, 2019, 48(9): 68-76. |
| [14] |
Mueller M, Smith N, Ghanem B. A benchmark and simulator for uav tracking[C]//Computer Vision-ECCV 2016. Cham: Springer, International Publishing, 2016: 445-461. DOI: 10.1007/978-3-319-46448-0_27.
|
| [15] |
Pu S, Song Y, Ma C, et al. Deep attentive tracking via reciprocative learning //Advances in Neural Information Processing Systems. 2018: 1931-1941.
|
| [16] |
Bertinetto L, Valmadre J, Golodetz S, et al. Staple: complementary learners for real-time tracking[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CPVR). June 27-30, 2016, Las Vegas, NV, USA. 2016: 1401-1409. DOI: 10.1109/CVPR.2016.156.
|
 2022, Vol. 39
2022, Vol. 39 


