2. 江苏师范大学, 江苏 徐州 221116;
3. 中国矿业大学信息与控制工程学院, 江苏 徐州 221116;
4. 中国科学院大学, 北京 100049
2. Jiangsu Normal University, Xuzhou 221116, Jiangsu, China;
3. School of Information and Control Engineering, China University of Mining and Technology, Xuzhou 221116, Jiangsu, China;
4. University of Chinese Academy of Science, Beijing 100049, China
近年来,以无线传感器网络(wireless sensor network, WSN)为代表的物联网技术在工业、农业、国防、医疗健康、家庭网络等领域发展迅猛。但传感节点能量受限问题制约了它的普及,其能量的高效利用引起大量学者的关注。其中功率放大器是传感节点通信发射单元的关键组成部分,实践中要求最大限度提高其功放效率和降低非线性失真。
目前抗功率放大器非线性失真技术主要有以下3类:第1类是优化功放设计,通常基于功放进行线性化设计[1],但是这种方法成本很高,同时功放效率较低。第2类从改变放大器特性、加大放大器“等效”线性区角度考虑,采用反馈、前馈和预失真线性化技术,这些技术可以显著改善系统性能[2],但同时也会引起更严重的带外泄露和性能的下降。第3类是基于改变信号特征,由于降低信号的峰值平均功率比(peak-to-average power ratio, PAPR)能在一定程度上提高功放效率和系统性能[3-5],考虑降低信号的PAPR或降低信号功率,如功率回退技术降低非线性失真。
在通信系统中目前通常采用较为先进的线性化技术设计功放,并且这类线性化技术常与功率回退技术相结合,此时功放整体以近似A类功放的方式工作[4, 6-9]。相较于其他抗非线性失真技术,功率回退法较低的复杂度更契合于WSN。然而,很少有文献研究功放的功率回退量、单载波调制成形滤波器的滚降系数与系统性能的关系[10-12]。当功放回退量偏大时,虽然能避免非线性失真,但发射功率降低,系统性能受到影响。反之,功率回退偏小则会造成严重的信号非线性失真。另外,不同的滤波器滚降系数会使得功率放大器输入功率出现波动,导致信号的星座图出现不同程度的弥散,与系统性能也密切相关。因而,当滤波器滚降系数不同时,如何选择合适的功率回退量是值得研究的问题。
由于WSN中数据速率通常较低,通常选用较为简单的单调制方式,本文以单载波正交幅值调制(quadrature amplitude modulation, QAM)为研究对象,将非线性放大器经过线性化技术补偿后等价为A类功放,从而分析信号的各项性能。为在功放效率较高的同时保证系统性能,需要在具有不同滚降系数的滤波器单载波系统中,找到最优的功放功率回退量,然而并没有一个闭合表达式能直接找到最优的功率回退量[13-14]。基于此,本文通过搭建单载波传输链路模型深入分析滤波器滚降系数、功放功率回退量对系统星座图、功率谱密度(power spectral density, PSD)、误符号率(symbol error rate, SER)3个性能参数的影响。通过仿真发现,当功放特性与滤波器滚降系数一定时,存在一个最优的功放输入功率回退,采用此输入功率回退能获得最优的系统性能。在搭建传输链路过程中,考虑到减小传输带宽和避免引入符号间干扰,发射端采用具有不同滚降系数的根升滤波器(square root raised cosine filter, SRRC)作为成形滤波器。
1 系统建模本文研究的通信系统结构如图 1所示。发射端信源产生二进制信号先经过QAM映射为复符号,再经过成形滤波器滤波后,通过放大器放大后发射,随后,信号经过高斯白噪声信道,传输至接收机端进行解调。

|
Download:
|
| 图 1 通信系统结构 Fig. 1 System model | |
为简化问题并突出重点,本文仅考虑基带传输链路模型,并且忽略载波引起的频率和相位偏移等对系统性能的影响。由于整个信号传输过程中,成形滤波器与放大器对信号的影响较大且不可忽视,因此本文将着重对成形滤波器与放大器模型进行分析,其通信系统原理简化模型如图 2所示。其中成形滤波器滤波后的信号记为s(t),信道噪声记为nGauss。

|
Download:
|
| 图 2 通信系统原理简化模型 Fig. 2 Simplified model of communication system principle | |
为避免相邻传输信号之间的串扰,通常引入成形滤波器产生合适的信号波形,从而有效限制带宽外信号,在保证信号没有码间串扰的情况下,既能最大限度地利用带宽,又能减少信号间的相互干扰。为避免传输过程中的符号间干扰,码元传输速率必须符合奈奎斯特第一准则。实际通信信道中一般使接收波形为升余弦滚降信号,该信号用发射端的基带成形滤波器和接收端滤波器两个环节同时实现,因此每个环节均为平方根升余弦滚降滤波器SRRC,两个环节合成实现升余弦滚降滤波。
本文以方形QAM信号为研究对象。输入信号通过成形滤波器后的输出信号表示为
| $ s(t) = {\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_n {\left( {{A_n} + {\rm{j}}{B_n}} \right)} g\left( {t - n{T_{\rm{s}}}} \right){{\rm{e}}^{{\rm{j}}2{\rm{ \mathit{ π} }}{f_c}t}}} \right\}, $ | (1) |
相应的等效复基带线性调制信号可表示为
| $ s(t) = \sum\limits_n {\left( {{A_n} + {\rm{j}}{B_n}} \right)} g\left( {t - n{T_{\rm{s}}}} \right), $ | (2) |
其中:An+jBn为经过QAM映射之后的复符号,g(t)为成形滤波器时域冲激响应。
根升余弦滚降滤波器的频率响应为
| $ H(f) = {\left[ {\frac{1}{2} + \frac{1}{2}\sin \frac{{\rm{ \mathit{ π} }}}{{2{f_{\rm{N}}}}}\left( {\frac{{{f_{\rm{N}}} - |f|}}{\alpha }} \right)} \right]^{\frac{1}{2}}}, $ | (3) |
时域冲激响应为
| $ g(t) = 4\alpha \frac{{\cos ((1 + \alpha ){\rm{ \mathit{ π} }}t/T) + \frac{{\sin ((1 - \alpha ){\rm{ \mathit{ π} }}t/T)}}{{4\alpha t/T}}}}{{{\rm{ \mathit{ π} }}\sqrt T \left( {{{(4\alpha t/T)}^2} - 1} \right)}}. $ | (4) |
其中:
实际的功率放大器经过非线性失真补偿后,可近似等价为理想A类功率放大器,其非线性特性曲线[4]通常表示为图 3。

|
Download:
|
| 图 3 理想A类功放非线性特性曲线 Fig. 3 Nonlinear characteristic of ideal class A power amplifier | |
其数学模型可表示为
| $ P(r)=\left\{\begin{array}{ll} r_{0, \max }\left(\frac{r}{r_{\max }}\right), & r<r_{\max } \\ r_{0, \max }, & r \geqslant r_{\max } \end{array}\right.. $ | (5) |
其中:ro, max=Armax,A表示放大器的放大倍数。
当输入功率接近非线性功放的压缩区或饱和点时,产生非线性失真,功放的增益出现下降。此时,通过降低放大器输入功率,使功放工作点偏离非线性区,可避免信号产生较大的失真。本文将输入功率回退(input power back-off, IBO)[4]定义为
| $ \mathrm{IBO}=\frac{r_{\mathrm{max}}^{2}}{P_{\mathrm{in}}}. $ | (6) |
通常,当信号的峰均比越大,为避免更多的非线性失真,功率回退必须更多。单载波系统中由于滤波器的存在,信号功率发生波动,信号功率较难计算,也给功率回退量的估计带来了困难。因而本文以仿真模拟为出发点,针对滤波器功率回退量对系统的影响进行研究探讨。
1.3 系统评价指标1) 星座图
星座图(constellation diagram)有助于定义信号元素的振幅和相位,非常适合评价多电平QAM的性能。在星座图中,一个信号元素用一个点表示。它携带的位或者位组合一般写在它的旁边。星座图有两根轴。水平X轴与同相载波相关,垂直Y轴与正交载波相关。图中每个点,可以包含4条信息。点在X轴的投影定义同相成分的峰值振幅,点在Y轴的投影定义正交成分的峰值振幅。点到原点的连线(向量)长度是该信号元素的峰值振幅(X成分和Y成分的组合),连线和X轴之间的角度是信号元素的相位。所有需要的信息都可以从星座图中轻易得到。
2) 功率谱密度
| $ P(f) = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}|S(f){|^2}, $ | (7) |
其中:T为符号周期,S(f)为能量信号s(t)的频谱密度,即
| $ S(f) = \int_{ - \infty }^\infty s (t){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathit{ π} }}ft}}{\rm{d}}t. $ | (8) |
3) 误符号率
误符号率SER根据理想矩形QAM信号在高斯白噪声信道中传输的误码率求得:
| $ {P_{\rm{s}}} = 4Q\left( {\sqrt {\frac{{3{\gamma _{\rm{s}}}}}{{M - 1}}} } \right), $ | (9) |
其中:γs为符号信噪比,M为调制阶数,Q(x)=
根据第1节中的系统模型,利用Matlab进行模型的搭建与仿真。重点从星座图失真、功率谱密度、误符号率等角度分析成形滤波器滚降系数和功放回退量对于系统的影响。实验参数如表 1所示。
|
|
表 1 仿真实验参数 Table 1 Parameters of simulation experiment |
根据前文介绍可知,不同的滤波器滚降系数导致功率放大器输入功率出现波动,相应的输出功率随之变化,星座图也受其影响。本文从星座图角度,分析当功率回退量相同时,不同滚降系数对信号星座图的影响,实验结果如图 4所示。
|
Download:
|
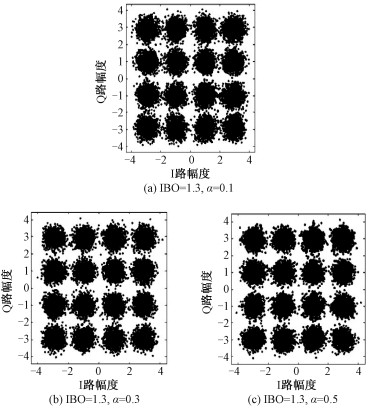
| 图 4 功率回退相同情况下,滚降系数滤波器对星座图影响 Fig. 4 Effect of filters with different roll-off coefficients on the constellation map | |
图 4展示在输入功率回退IBO均为1.3的条件下,不同滚降系数的滤波器对星座图的影响结果。图 4(a)为滚降系数α=0.1时的星座图,平均误差矢量幅度EVM=19.2%,图 4(b)为滚降系数α=0.3时的星座图,平均误差矢量幅度EVM=14.8%,图(c)为滚降系数α=0.5时的星座图,此时EVM=3.1%。从图 4可以看出,当功率回退相同时,滚降系数越小,星座图上不同位置的信号间隙越小,信号离散化越严重,信号失真越严重。
2.2 功率谱密度根据前文介绍可知,成形滤波器不同的功率回退量和滚降系数均影响功率放大器输出信号的频谱扩展。从功率谱密度角度,分析不同功率回退量和滚降系数对功率谱密度的影响,实验结果如图 5(a)、5(b)所示。

|
Download:
|
| 图 5 输入功率回退与滤波器滚降系数对功放输出信号功率谱密度的影响 Fig. 5 Effect of input power backoff and roll-off coefficients on the power spectral density of output signal | |
图 5(a)描述输入信号经过不同功率回退后通过功率放大器的功率谱密度。图中3条曲线分别表示不同功率回退情况下,功率放大器的输出信号功率谱密度。对比功率放大器的输入和输出信号功率谱密度可看出,功放非线性能引起信号频谱扩展,从而带来带外干扰。功率回退越小,信号失真越严重,带外干扰越严重。当功率回退量较小,功放工作在近饱和区时,引起较强的频谱扩展以及带外干扰。
图 5(b)为相同的功率回退时,信号经过不同滚降系数滤波器成形后,通过功率放大器输出的功率谱密度。在功率放大器输入功率回退相同的情况下,对比不同滚降系数的成形滤波器对应的两种情况可以发现,成形滤波器滚降系数越小,对应的信号带外扩展越严重,从而带外干扰越强。这是因为滤波器滚降系数越小,信号功率波动的概率越大[14]。
2.3 误符号率分析通过2.1与2.2节中对星座图与功率谱密度分析,概括描述了QAM信号的失真情况。本小节从误码率角度,分析滚降系数和功率回退对系统QAM性能的影响,实验结果如图 6所示。

|
Download:
|
| 图 6 输入功率回退与滤波器滚降系数对误符号率影响 Fig. 6 Effect of input power backoff and roll-off coefficients on symbol error rate | |
本节中的理论SER根据理想矩形QAM信号在高斯白噪声信道中传输的误码率Ps=
图 6(a)为滚降系数α=0.1条件下,高斯白噪声信道中的误符号率SER与输入功率回退IBO之间的关系曲线。图中的实线为存在非线性失真时的SER与IBO之间的关系曲线,虚线为理论SER曲线。从图中可看出,当存在非线性失真时,存在某个特定的IBO对应最低的SER,根据该特定的关系即可取得最佳的系统性能。当滚降系数为0.1时,对应最佳性能的IBO为1.5,此时输入信号峰均比为PAPR=5.7。
图 6(b)为滚降系数α=0.5时,SER与IBO之间的关系曲线。从图中可以看出,存在最佳系统性能的IBO。当滚降系数为0.5时,对应最佳性能的IBO为1.1,此时输入信号的峰均比为PAPR=3.5。
对比图 6(a)和图 6(b)可以发现:1)存在某个最优IBO使得系统SER最小,此时可取得最佳的系统性能,且该IBO与滤波器滚降系数相关联;2)为达到某一特定的系统性能(非最佳系统性能),除放大器线性区外,在非线性区内同样存在一个IBO能达到同样的系统性能;3)滚降系数越小,IBO越大才能保证达到最优的系统性能。这是因为当滚降系数越小时,信号峰均比PAPR越大,因此需要的IBO也就越大。
3 结论本文分析在采用单载波调制的WSN中功率放大器非线性失真对系统性能的影响。在高斯白噪声信道中,从滤波器滚降系数与功放输入功率回退两个角度分析功放非线性特性对于信号星座图、功率谱密度和误符号率3个方面的影响。经过仿真分析发现,总存在某个输入功率回退对应最佳的QAM性能。当成形滤波器滚降系数越小时,功放输出信号频谱扩展更为严重,同时对应最佳性能需要的输入功率回退量越大。在后续研究中,将在本工作的结论基础上,在不同滚降系数滤波器条件下,优化输入功率回退,在同时考虑系统误符号率与放大器效率两种条件下使系统取得最优性能。
| [1] |
栾慎吉, 包建荣, 刘超. 有记忆功放的非线性测试及其预失真器设计[J]. 实验室研究与探索, 2017, 36(6): 42-46. Doi:10.3969/j.issn.1006-7167.2017.06.011 |
| [2] |
张小梅. 基于数字预失真技术的功放线性化研究[D]. 西安: 西安电子科技大学, 2012.
|
| [3] |
Madani M H, Abdipour A, Mohammadi A. Analysis of performance degradation due to non-linearity and phase noise in orthogonal frequency division multiplexing systems[J]. Iet Communications, 2010, 4(10): 1226-1237. Doi:10.1049/iet-com.2009.0439 |
| [4] |
Ochiai H. An Analysis of Band-limited communication systems from amplifier efficiency and distortion perspective[J]. IEEE Transactions on Communications, 2013, 61(4): 1460-1472. Doi:10.1109/TCOMM.2013.020413.120384 |
| [5] |
Jiang T, Li C, Ni C. Effect of PAPR reduction on spectrum and energy efficiencies in OFDM systems with Class-A HPA over AWGN channel[J]. IEEE Transactions on Broadcasting, 2013, 59(3): 513-519. Doi:10.1109/TBC.2013.2253814 |
| [6] |
李频钟, 王海燕, 朱新宁, 等. TD-SCDMA HSUPA终端功率回退[C]//陶小雪. 全国第4届信号和智能信息处理与应用学术会议. 上海: 《计算机工程与应用》杂志社, 2010: 92-96.
|
| [7] |
游伟, 郭道省, 易旭. 无线信道中功放非线性失真补偿技术研究[J]. 无线通信技术, 2016, 25(1): 11-16. Doi:10.3969/j.issn.1003-8329.2016.01.003 |
| [8] |
彭晶波. 非线性失真环境下的多载波系统优化[D]. 合肥: 中国科学技术大学, 2008.
|
| [9] |
冯晓春. 数字QAM信号在传输链路中的非线性失真表现[J]. 有线电视技术, 2017(3): 67-69. |
| [10] |
韩冰, 晋东立. 卫星通信中16QAM信号的数字预失真研究[J]. 飞行器测控学报, 2015, 34(2): 184-188. |
| [11] |
李明玉, 何松柏. 卫星通信系统中适用于16QAM信号的一种预失真方法[J]. 电子测量与仪器学报, 2009, 23(12): 8-13. |
| [12] |
陈毅雯. OFDM系统中非线性失真下的节能算法研究[D]. 北京: 北京邮电大学, 2013.
|
| [13] |
Dimakis C E, Kouris S S, Kosmopoulos S A. Performance evaluation of 16-QAM signalling through nonlinear channels in an AWGN and interference environment: a simulation approach[J]. IEE Proceedings I-Communications, Speech and Vision, 1990, 137(5): 315-322. Doi:10.1049/ip-i-2.1990.0044 |
| [14] |
Ochiai H. Exact and Approximate distributions of instantaneous power for pulse-shaped single-carrier signals[J]. IEEE Transactions on Wireless Communications, 2011, 10(2): 682-692. Doi:10.1109/TWC.2011.120810.100755 |
 2021, Vol. 38
2021, Vol. 38 


