2. 中国科学院大学, 北京 100049;
3. 上海科技大学, 上海 201210
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. ShanghaiTech University, Shanghai 201210, China
卫星作为一个复杂度较高、涉及技术较广且造价昂贵的综合性系统,由于所处空间环境的不确定性以及发射前测试的局限性,在轨运行期间不可避免地会出现一些异常或故障。在卫星故障早期及时发现遥测数据异常对延长卫星使用寿命,保证卫星通信、导航、遥感等任务的连续性,提高卫星在轨运行的安全性都具有重大意义。
目前,国内工程上普遍采用设置阈值[1]的方法和专家系统[2]的方法对遥测数据进行异常检测。设置阈值的方法需要根据以往的工程经验和专家经验对部分遥测参数设定门限,将超出门限的数据标记为异常数据。这种方法简单有效,误检率低,但是有许多故障发生时遥测参数并不会超出所设门限。而且这种方法需要耗费大量的人力物力,可扩展性低。专家系统需要依据大量的专家知识和以往的故障库建立数学、物理模型,以此自动检测卫星故障和数据异常。专家系统的异常检测能力要远大于设置阈值的方法,但是卫星设计结构复杂,很难建立准确且完备的模型,而且专家系统无法检测到未知的异常。
随着卫星数量不断增加,从卫星传到地面的数据也在源源不断地增加,数据中包含的大量信息亟需挖掘。基于数据驱动的异常检测方法[3-6]从数据出发,不需要专家知识和精确的数学物理模型,有较好的扩展性。基于数据驱动的异常检测方法主要可以分为基于机器学习的检测方法以及它们的衍生算法和基于统计的异常检测方法。例如Ma和Perkins[7]以及Cohen等[8]使用单分类支持向量机(one-class SVM,OCSVM)[9]将数据映射到高维空间,寻求一个超平面将正常数据和异常数据以最大间隔分开,一旦数据越过该超平面即认为发生异常。但是,寻求最优超平面是个二次规划问题,计算量较大,当数据不是球型时效果较差。针对大量具有相关性的多维遥测参数,李楠等[10]利用主成分分析(principal component analysis, PCA)[11-12]方法分析卫星不同的故障模式,通过检测特征值之间相应比例的变化进行异常判决。但是PCA方法也有一些局限性,在非高斯分布情况下,PCA方法得出的主元可能并不是最优的;针对变化的大规模数据源,聚类算法如增量聚类[13-14]可以有效解决原有类别与新加入数据不匹配的问题,而且不需要很大的储存空间,但是对参数敏感度比较高。
虽然国内已经开始结合机器学习等方法对在轨卫星遥测数据智能化、自动化的检测进行研究,但是目前仍处于理论阶段,还没有应用到工程中去。对于在轨故障和遥测异常,主要还是通过设置的工程阈值来检测,但是许多隐藏在门限内的故障征兆无法被及时检测到,造成严重后果。如图 1所示,故障早期出现异常征兆但未超出报警门限。2018年,某在轨卫星的扩频应答机出现严重故障,与之相关的参数主要有温度、电压、电流、功率等,温度参数具有强周期性,随着卫星绕地球运行不断发生变化,且升降幅度比较大,电压等参数为稳态型参数,波动非常小。该故障在早期已经出现异常征兆,由于温度参数的异常程度远小于自身的周期性升降幅度,虽然许多与温度相关的参数也发生相应改变,但是这些参数始终未超出所设门限,因此没有及时预警,最终导致整颗卫星失去功能,造成重大事故。

|
Download:
|
| 图 1 门限内的故障早期征兆 Fig. 1 Signs of early failure within threshold | |
根据以往的工程经验,卫星上许多故障都与温度有关,对于此类隐藏在门限内且故障相关参数具有周期性和相关性的故障,设置更合理的阈值可以在一定程度上减轻问题。但是只能针对单一参数做异常检测,无法挖掘多参数间相关性的异常变化。而且目前的理论研究多集中在检测遥测参数的单点异常,而卫星遥测数据量非常庞大,有时还会受到下传错误的影响,单点异常往往可信度较低。Ding等[15]提出潜在相关性的概念,通过假设高斯模型分析混凝土泵车每个工作时段内参数间的相关性变化,检测混凝土泵车的异常模式,具有较高的可靠性。Zhong等[16]使用相关系数替代特征值改进模型,在高维空间对多元正态模型进行3σ检测,并且在低维空间验证了该种方法的优越性。
但是,卫星故障往往需要涉及高维遥测参数,这使得概率分布模型复杂度增加,计算难度增大。而且高维空间本身具有稀疏性,一维正态分布有68%的值落于正负标准差之间,而在十维空间上只有0.02%的值落于正负标准差之间,通常3σ检测法则只适用于单参数的异常检测。另外,以上模型虽然可以通过相关性的变化来检测故障早期征兆,但是无法确定发生异常的具体参数。因此,本文在分析参数间相关性的基础上融合主成分分析的原理,并做出相应改进,应用到在轨卫星数据异常检测中。通过提取遥测参数间的相关系数构建相关概率模型,引入主成分分析的方法将高维模型映射到低维空间,并根据T2统计量检测异常,检测到异常后再重构回原空间,通过计算重构误差比例确定发生异常的参数。
1 基于相关概率模型的异常检测根据以往积累的工程经验,在卫星故障早期,卫星各项功能正常,但是某些遥测参数已经开始发生缓慢变化,此时卫星处于一种亚健康状态。卫星的一些遥测参数间存在某种相关性,卫星处于正常状态时,这些遥测参数间的相关性保持稳定或者变化较小;卫星处于异常状态时,与故障相关的遥测参数同时受到故障影响,其相关性可能会发生较大的变化。因此,针对这类故障前后相关性发生变化的故障,本文使用基于相关概率模型的异常检测方法来检测卫星不同周期相关性的异常模式,主要包含以下几个步骤。
1.1 划分工作单元卫星遥测数据是一系列多元时间序列,而且许多遥测参数具有周期性,尤其是与温度相关的遥测参数。不同周期参数间相关性的变化可能会反映出卫星异常,而且相对于单点异常,较长时段的异常具有更高的可信度。因此以卫星绕地运行一圈为一个工作单元,对遥测数据进行划分,一个工作单元的长度刚好与大部分温度参数一个周期的长度相同。这样,遥测数据便被划分成一系列的工作单元,如图 2所示。
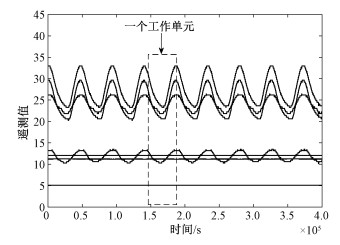
|
Download:
|
| 图 2 工作单元划分示意图 Fig. 2 Graph of work unit division | |
在一个工作单元内,各个遥测参数都是长度相等的一元时间序列。计算相关性的方法有很多种[17]。由于同一数据集中的遥测参数具有不同的量纲,与协方差相比,相关系数更适合描述各种遥测参数之间的相关性,相关系数越大,相关性越强。本文通过计算皮尔逊相关系数来量化遥测参数间的相关性,计算公式为
| $ r_{\boldsymbol{xy}}=\frac{\sum \nolimits_{i=1}^{n}\left(\boldsymbol{x}_{i}-\overline{\boldsymbol{x}}\right)\left(\boldsymbol{y}_{i}-\overline{\boldsymbol{y}}\right)}{\sqrt{\sum \nolimits_{i=1}^{n}\left(\boldsymbol{x}_{i}-\overline{\boldsymbol{x}}\right)^{2} \sum \nolimits_{i=1}^{n}\left(\boldsymbol{y}_{i}-\overline{\boldsymbol{y}}\right)^{2}}}, $ | (1) |
其中:n为一个工作单元内时间序列的长度,xi、yi分别为参数x、y在某一时刻的遥测值, x、y分别为参数x、y在该工作单元内遥测值的平均值, rxy的取值范围为-1~1。
之后,计算一个工作单元内每2个遥测参数间的相关系数,这些相关系数便构成该工作单元的相关系数向量。
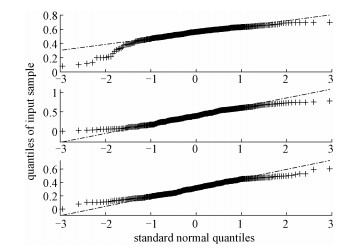
1.3 构建相关概率模型假定划分了M个工作单元,即卫星绕地运行M圈,经计算得到M个相关系数向量。正常情况下,卫星每个运行周期情景相似,考虑到地面上人为操作、空间环境不确定因素以及遥测数据下传错误等影响,总体来看,正常的相关系数向量占大多数,异常的相关系数向量只占一小部分。由大数定律可知,当M足够大时,相关系数向量渐近服从多元正态分布[16]。对于数据来源于多元正态总体的判断,目前没有很好的办法,但是如果一个p维的向量服从p元正态分布,则它的每一个分量都服从一元正态分布。如图 3所示,将几个遥测参数的相关系数向量的每一维作Q-Q图。
|
Download:
|
| 图 3 相关系数向量的Q-Q图 Fig. 3 Quantile-quantile plot of correlation coefficient vectors | |
要利用Q-Q图鉴别数据是否近似于正态分布,只需看Q-Q图上的点是否近似地在一条直线附近。图 3显示,相关系数向量的每一个分量都来自于一个一元正态分布。
1.4 对相关概率模型应用PCA多维遥测数据建立相关概率模型后,可能会造成“维度灾难”,为后续检测增大难度,而且相关系数向量的元素中存在一定的相关性,可能存在信息重叠,PCA方法可以将高维向量映射到低维空间来解决这一问题。
PCA的实质是从存在相关的多维度原始向量空间中抽取出几个彼此正交的主成分代表原始数据,从而简化分析模型,这些主成分包含原始数据大部分的信息。为实现降维,就要使降维后的结果尽量分散(重叠太多就不能很好地复原回去),同时,希望尽可能保留更多的原始信息,因此,投影后的各主成分之间是正交的,而且在投影后每一维度上方差最大。PCA方法的主要流程如下:
1) 将原始数据矩阵零均值化;
2) 求出协方差矩阵;
3) 计算协方差矩阵的特征值和对应的特征向量;
4) 将特征向量按对应特征值大小排列成矩阵,取前k个组成矩阵P(保留最大的k个特征向量);其中,主成分对应的方差在总方差中的占比为该主成分的贡献率,主成分λk的贡献率表示为
| $ \frac{\lambda_{k}}{\sum \nolimits_{i=1}^{p} \lambda_{i}}, $ | (2) |
按照所需贡献率选择主成分及其对应的特征值和特征向量,最终得到的主元模型为
| $ \widehat{\boldsymbol{X}}=\boldsymbol{X} * \boldsymbol{A}, $ | (3) |
其中: X是原始高维数据,A是转换矩阵。
1.5 T2统计量的异常检测基于PCA的异常检测通常使用T2统计量来检测过程是否异常,T2统计量可以衡量变量在主成分空间的变化,检测函数为
| $ T^{2}=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{\varLambda}^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{x} \leqslant T_{\alpha}^{2}, $ | (4) |
其中: x为样本的相关系数向量,Λ=diag{λ1, …, λk},Tα2为置信度为α的T2控制限
| $ T_{\alpha}^{2}=\frac{k\left(p^{2}-1\right)}{p(p-k)} F_{k, p-k ; \alpha}, $ | (5) |
式中:Fk, p-k; α第一自由度为k,第二自由度为p-k的F分布,α通常取0.01、0.5和0.1。
测试样本应满足T2≤Tα2,否则判定为异常。
1.6 进一步确定异常遥测参数通过上述方法检测出异常后,再将低维空间的数据重构到高维空间,并计算重构高维数据和原始高维数据的重构误差和每个分量对重构误差的贡献比例,贡献比例越大,该分量出现异常的可能性就越高,交叉对比贡献比例较大的分量可以大致确定发生异常的遥测参数,进而为后续的故障定位确定方向。
重构误差的计算公式为
| $ U=\|\widehat{\boldsymbol{X}}-\boldsymbol{X}\|_{2}, $ | (6) |
其中:X是原始高维数据,
| $ \widehat{\boldsymbol{X}}=\boldsymbol{X} * \boldsymbol{A} * \boldsymbol{A}^{\prime}+\overline{\boldsymbol{X}}, $ | (7) |
其中:A是转换矩阵,X是原始高纬数据的均值。
计算每个分量对重构误差的比例,公式为
| $ u_{i j}=\frac{\left\|\widehat{\boldsymbol{X}}_{i j}-\boldsymbol{X}_{i j}\right\|_{2}}{U_{i}}. $ | (8) |
其中:Xij表示第i个原始数据的第j个分量,
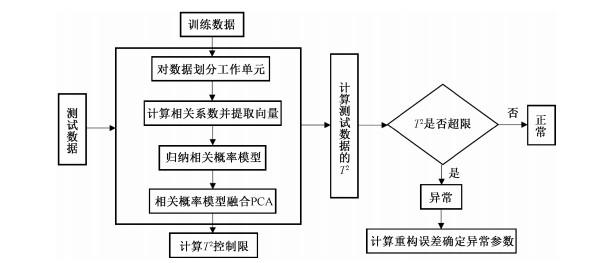
本文所提出的基于相关概率模型的异常检测方法的流程如图 4所示。
|
Download:
|
| 图 4 基于相关概率模型的异常检测方法流程图 Fig. 4 Flow chart of anomaly detection method based on correlation probability model | |
本文以某型号在轨卫星的扩频应答机故障为故障案例,将与扩频应答机相关的温度、电压、功率等共10个遥测参数作为待检测参数,选取2018年7月到10月的遥测数据为实验对象。样本量为5 215 000条,遥测数据采样率为1条/s,将7、8月份的正常数据作为训练数据,9、10月份故障发生前后的数据作为测试数据,验证基于相关概率模型的PCA检测方法的有效性,并和其他方法进行比较。
2.1 实验准备对于卫星这种具有高复杂度且造价昂贵的系统,在故障早期检测出系统异常具有重大意义,发现异常的时间越早,地面运管人员进行故障排除和远程指令修复就越及时,造成的损失也就越小。因此,将检测出系统参数异常的时间作为检测方法的一个评价指标。
另外,通过表 1所示的混淆矩阵[18]计算检测方法的准确率(Accuracy)、虚警率(False Alarm)和召回率(Recall),计算公式分别如下:
| $ \begin{array}{l} \text { Accuracy }=\frac{T_{\mathrm{N}}+T_{\mathrm{P}}}{F_{\mathrm{N}}+T_{\mathrm{P}}+F_{\mathrm{P}}+T_{\mathrm{N}}} \times 100 \%, \\ \text { False Alarm }=\frac{F_{\mathrm{P}}}{F_{\mathrm{P}}+T_{\mathrm{P}}} \times 100 \%, \\ \text { Recall }=\frac{T_{\mathrm{P}}}{F_{\mathrm{N}}+T_{\mathrm{P}}} \times 100 \%. \end{array} $ | (9) |
|
|
表 1 混淆矩阵 Table 1 Confusion matrix |
其中,TN为被正确识别出的正常数据,FP为被误判为异常数据的正常数据;FN为被识别为正常数据的异常数据,TP为被正确判别的异常数据。
2.2 实验结果 2.2.1 异常检测结果和对比作为对照,本文采用基于PCA的异常检测方法和基于相关系数向量的方法对同一数据集进行异常检测,验证相关性变化可以反映早期故障征兆,以及工作单元的模式异常比遥测数据的单点异常具有更高的可靠性。
对于基于PCA的异常检测方法,本文以采样率1条/10 min对遥测数据进行采样,然后直接将训练数据映射到主元空间,分别计算T2控制限,置信度α分别取0.01、0.05和0.1,然后将测试数据映射到同一主元空间,计算测试数据的T2统计量并对T2统计量做异常检测。
基于相关系数向量方法不需要建立模型,直接对1.2节中的相关系数向量进行计算分析。它首先计算训练数据中相关系数向量的均值向量,然后求出训练数据中每个相关系数向量到均值向量的欧式距离,假设第k个样本向量到均值向量的距离为lk,将距离从大到小排序,样本量为m,阈值设定为
表 2显示3种方法在不同置信度下检测到异常的时间,可以看出,3种办法都可以提前20多天对故障进行预警。
|
|
表 2 检测到异常的时间 Table 2 Anomaly detection time |
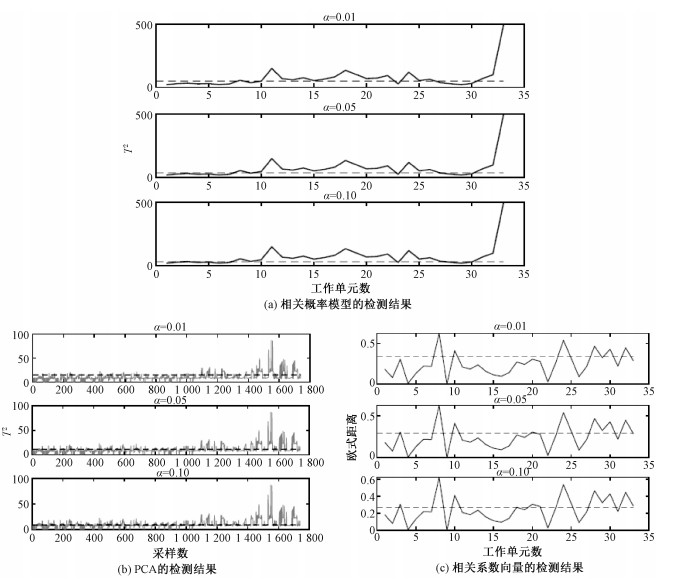
图 5(a)、5(b)、5(c)分别为基于相关概率模型的异常检测结果、直接对遥测数据进行PCA异常检测结果和基于相关系数向量的异常检测结果。基于PCA的异常检测方法虽然能更早地检测出数据异常,但是由于遥测数据中的温度参数周期内变化幅度大,占据最重要的主成分,虽然在故障早期有总体上升的趋势,但是异常程度远小于自身的变化幅度,而且在周期内下降的过程中,又会被判定为正常,导致检测结果极不可靠。基于相关概率模型的异常检测方法在置信度为0.1时最早检测到异常,这种结果是合理的,因为可靠性和置信度往往成反比,置信度α越小,检测出异常数据的时间越晚,这是牺牲时间来提高检测可靠性的结果,而且在3种置信度下,不同工作单元的异常模式大部分都能被检测到。基于相关系数向量的检测方法虽然也能够在早期检测到异常,但是由于在高维空间检测的局限性导致中间部分出现很多漏警的情况。
|
Download:
|
| 图 5 3种方法的检测结果 Fig. 5 Detection results of three methods | |
进一步分别计算3种方法的评价指标如下,从表 3可以看出,基于相关概率模型的检测方法的准确率和召回率分别明显高于其他2种方法,而且虚警率也最低,具有较高的可靠性,证明通过分析参数间的相关性,能够降低温度参数作为主成分对检测结果的负面影响,使检测结果更加合理,而且工作单元的异常模式比单点异常更具可信度。
|
|
表 3 检测结果的评估 Table 3 Evaluation of detection results |
在检测出异常之后,计算相关系数向量的重构误差和每个分量(即某2个遥测参数的相关系数)对重构误差的贡献比例进一步判定发生异常的遥测参数。
表 4显示相关系数向量的分量对重构误差的贡献比例。由于划分的工作单元和相关系数向量包含的分量都比较多,这里只选取某工作单元的几个重要遥测参数间的相关系数。
|
|
表 4 相关系数对重构误差的贡献比例 Table 4 Contribution ratio of correlation coefficient to reconstruction error |
表 4中,V5, A、V12, A分别代表扩频A的+5 V和+12 V电压,TA、TB分别代表扩频A和扩频B的温度,V5, B、V12, B分别代表扩频B的+5 V和+12 V电压。扩频B并未发生故障,因此与之有关的遥测参数间的相关系数对重构误差的贡献很小,几乎可以忽略不计。而与扩频A+5 V电压和扩频A温度有关的遥测参数间的相关系数对重构误差的贡献很大,因此可以判断出遥测参数间的相关性发生了变化,通过进一步地交叉对比可以发现是扩频A+5 V电压和扩频A温度这2个遥测参数发生严重异常。
2.3 实验结果分析如图 6(a)所示,正常情况下,扩频A+5 V电压稳定在5.07 V,偶尔会在5.07~5.10 V之间波动,扩频A温度在23.2~32.9 ℃间呈周期性变化,扩频A+5 V电压与扩频A温度之间的相关性很弱。而在故障早期,扩频A温度在25.6~35.5 ℃间呈周期性变化,较正常情况下,温度整体小幅上升,而且扩频A+5 V电压超出正常范围的上限5.1 V,且在扩频A温度的一个周期内,扩频A+5 V电压随着温度的升高而增大,随着温度的降低而减小,即这2个遥测参数之间的相关性增强了。图 6(b)对比在同一时间间隔内,正常情况下和故障早期扩频A+5 V和扩频A温度之间的相关性,还是用相关系数表示2个遥测参数间的相关性,可以看出,在故障早期,二者之间的相关性总体上较正常情况下的相关性强。

|
Download:
|
| 图 6 正常情况和异常情况的对比图 Fig. 6 Comparison of normal and abnormal conditionsn | |
故障发生前后,与故障相关的参数始终在阈值范围内波动,得益于遥测参数间相关性的敏感性。本文所采用的基于相关概率模型的异常检测方法能够在故障早期就捕捉到遥测参数间相关性的异常征兆,而且可以通过对重构误差的贡献比例确定异常参数,以便进行下一步故障诊断,对卫星的健康维护具有重大意义。
3 总结卫星平台的连续型遥测参数主要是电压、电流、温度等参数。根据以往的工程经验,与温度相关的故障占很大比例,对于卫星上与温度相关的具有周期性的遥测参数,工程上常用的方法无法在故障早期检测出数据异常。本文采用一种基于相关概率模型的PCA异常检测方法,根据卫星的工作周期对数据进行划分,以工作单元的形式研究遥测参数间的相关性变化,比检测单点异常更具信服力,并使用PCA的方法对多元分布模型进行降维。而且,本文通过检验T2统计量的方法对数据是否异常进行判决,避免阈值设置的困扰。另外,在检测出异常数据之后,还可以通过计算重构误差贡献比例确定发生异常的遥测参数,为后续的故障诊断确定大致方向。
实验证明,基于相关概率模型的PCA异常检测方法可以快速、准确地在故障早期检测出遥测数据的异常,并进行初步的故障定位,这对提高卫星的可靠性和安全性具有重大意义。
| [1] |
Yairi T, Kawahara Y, Fujimaki R, et al. Telemetry-mining: a machine learning approach to anomaly detection and fault diagnosis for space systems[C]//2nd IEEE International Conference on Space Mission Challenges for Information Technology(SMC-IT'06), Pasadena, CA, USA: IEEE Press, 2006: 466-476.
|
| [2] |
Hayden S C, Sweet A J, Christa S E, et al. Advanced diagnostic system on earth observing one[C]//Proceedings of AIAA Space 2004 Conferace and Exhibit, 2004: 14.
|
| [3] |
彭喜元, 庞景月, 彭宇, 等. 航天器遥测数据异常检测综述[J]. 仪器仪表学报, 2016, 37(9): 1929-1945. Doi:10.3969/j.issn.0254-3087.2016.09.003 |
| [4] |
Chandola V, Banerjee A, Kumar V. Anomaly detection: a survey[J]. ACM Computing Surveys, 2009, 41(3): 1-58. |
| [5] |
Song X Y, Wu M X, Jermaine C, et al. Conditional anomaly detection[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(5): 631-645. Doi:10.1109/TKDE.2007.1009 |
| [6] |
谢锦生, 郭立, 陈运必, 等. 基于时空惊奇计算的视频异常检测方法[J]. 中国科学院研究生院学报, 2013, 30(1): 83-89. |
| [7] |
Ma J, Perkins S. Time-series novelty detection using one-class support vector machines[C]//Proceedings of the International Joint Conference on Neural Networks, 2003. Portland, CR, USA: IEEE Press, 2003: 1741-1745.
|
| [8] |
Cohen G, Hilario M, Pellegrini C, et al. One-class support vector machines with a conformal kernel: a case study in handling class imbalance[C]//Structural, Syntactic, and Statistical Pattern Recognition. Springer-Verlag Berlin Heidelberg, 2004, 3138: 850-858.
|
| [9] |
陈斌. 异常检测方法及其关键技术研究[D]. 南京: 南京航空航天大学, 2013.
|
| [10] |
李楠, 张云燕, 李言俊. 一种自旋稳定卫星姿态传感器数据异常的诊断方法[J]. 宇航学报, 2011, 32(6): 1327-1332. Doi:10.3873/j.issn.1000-1328.2011.06.019 |
| [11] |
Spiegelberg J, Rusz J. Can we use PCA to detect small signals in noisy data?[J]. Ultramicroscopy, 2017, 172: 40-46. Doi:10.1016/j.ultramic.2016.10.008 |
| [12] |
Wang X, Kruger U, Irwin G W, et al. Nonlinear PCA with the local approach for diesel engine fault detection and diagnosis[J]. IEEE Transactions on Control Systems Technology, 2008, 16(1): 122-129. Doi:10.1109/TCST.2007.899744 |
| [13] |
Iverson D L, Martin R, Schwabacher M, et al. General purpose data-driven monitoring for space operations[J]. Journal of Aerospace Computing, Information, and Communication, 2012, 9(2): 26-44. Doi:10.2514/1.54964 |
| [14] |
Iverson D L. Inductive system health monitoring[C]//Proceedings of the International Conference on Artificial Intelligence & Proceedings of the International Conference on Machine Learning: Models, Technologies & Applications, Las Vegas, Nevada, USA, 2004: 605-611.
|
| [15] |
Ding J W, Liu Y B, Zhang L, et al. An anomaly detection approach for multiple monitoring data series based on latent correlation probabilistic model[J]. Applied Intelligence, 2016, 44(2): 340-361. Doi:10.1007/s10489-015-0713-7 |
| [16] |
Zhong S S, Luo H, Lin L, et al. An improved correlation-based anomaly detection approach for condition monitoring data of industrial equipment[C]//2016 IEEE International Conference on Prognostics and Health Management (ICPHM). Ottawa, ON, Canada: IEEE Press, 2016: 1-5.
|
| [17] |
Reshef D N, Reshef Y A, Finucane H K, et al. Detecting novel associations in large data sets[J]. Science, 2011, 334(6062): 1518-1524. Doi:10.1126/science.1205438 |
| [18] |
Pang J Y, Liu D T, Peng Y, et al. Anomaly detection based on uncertainty fusion for univariate monitoring series[J]. Measurement, 2017, 95: 280-292. Doi:10.1016/j.measurement.2016.10.031 |
 2021, Vol. 38
2021, Vol. 38 


