2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
传统的遥感卫星获取的数据基本都是图像形式,如光学遥感图像、SAR遥感图像[1]。随着遥感卫星技术的不断发展,新型的视频遥感卫星开始进入应用领域[2]。2011年欧洲的Astrium公司发射1颗静止轨道监视系统卫星,美国的Skybox Imaging公司在2013年发射1颗业务型的视频卫星—“Skysat-1”,加拿大同年在国际空间站安装视频成像载荷,两者的分辨率都达到1 m。中国首颗视频成像卫星“天拓-2”在2014年升空,分辨率5 m,帧率为25 s/帧,为中国的卫星实时成像奠定了基础。2015年由中国长光卫星技术有限公司独立研发的“吉林一号”卫星,截至2018年在轨卫星数量增至10颗[3]。
视频遥感卫星对灾害监测、道路交通导航、军事战略指导等方面都具有重要作用。在实际应用中,目标的检测跟踪具有广阔应用场景。运动目标检测是从视频或图像序列中提取运动目标的过程,是后续进行目标跟踪和分类识别的前提和基础[4]。对于视频运动目标的检测问题,目前有2个研究方向:第1种是先对单帧图像进行目标检测,再根据帧与帧之间像素点的关联性确定目标运动方向; 第2种是直接基于视频或者图像序列,利用不同时刻视频流的信息差异进行检测。后者的检测算法主要有光流法、帧间差分法和背景差分法3种[5]。
过去几十年,目标跟踪方法经历了从卡尔曼滤波等经典跟踪方法,到基于相关滤波方法,再到深度学习相关方法的演变历程[6]。根据建模方式的不同,将目标跟踪方法分为生成式模型方法和判别式模型方法[7-8]。与前者相比,判别式的分类器采用机器学习,训练中用到背景信息,使得分类器区分前景和背景能力加强,相对而言判别类方法效果较好。
随着遥感领域目标检测跟踪应用越来越广泛,许多学者投入到相关研究中。Meng和Kerekes[9]提出一种多角度高分辨率多光谱卫星图像的3步处理算法,包括运动目标估计、目标建模、目标匹配。吴佳奇等[10]以卫星视频中的运动目标为点目标,引入一种基于运动平滑度约束的贝叶斯分类方法,实现了高性能跟踪。Du等[11]使用三帧差分法和相关滤波进行卫星视频的检测跟踪,同时Du等[12]又提出一种多帧光流检测跟踪器,以进一步提高对卫星视频的检测跟踪性能。此外,Shao等[13]提出一种VCF(velocity correlation filter) 算法,利用光流和惯性机制提取的速度特征构造卫星视频目标跟踪的滤波核。
对于视频遥感图像的运动目标检测问题,很难直接使用传统的检测跟踪方法,原因在于:1)待检测目标尺寸。遥感图像拍摄平台距离地表远,运动目标往往只占据几个像素,轮廓不清晰。2)背景的复杂性。遥感图像由于拍摄范围广,包含的地物信息丰富,背景复杂度较高,目标与背景像素的对比度较小,难以完全将目标分离出来。
1 总体流程针对卫星视频运动目标检测跟踪问题,本文提出一种基于V-CSK(ViBe-CSK)的目标检测跟踪算法,主要利用改进的ViBe算法实现目标检测[14],并引入多重自定义阈值滤波和目标中心位置均值估计原理提取运动目标中心点信息,同时加入噪声距离判断原则和目标轨迹预测插值减少噪声干扰,最后利用CSK算法实现卫星视频运动目标跟踪[15]。实验同时还设置3组目标检测对照组和9组目标跟踪对照组作为结果参照。
V-CSK目标检测跟踪算法流程如图 1所示。

|
Download:
|
| 图 1 基于V-CSK运动目标检测跟踪流程 Fig. 1 Moving target detection and tracking process based on V-CSK | |
1) 利用改进的ViBe算法进行背景模型构建,采用背景差分法获得运动目标的检测图。
2) 对检测图采用多重自定义阈值滤波算法计算运动目标中心区域。根据目标大小选择合适的滤波次数和滤波模板大小,实现不同尺寸的目标中心区域提取。在计算过程中加入噪声距离判断原则,减少噪声对中心区域结果的影响。
3) 采用中心位置均值原理对中心区域中的像素点进行计算,得到下一帧的运动目标的预测位置。
4) 对下一帧运动目标的预测结果进行轨迹拟合,当某一帧的预测结果明显偏离曲线时,则丢弃该点坐标,同时采用插值法进行位置填充,得到校正后的预测位置。
5) 利用校正后预测位置构建GGT(generated-ground-truth)数据,并传递到基于CSK算法的跟踪器,从而实现运动目标跟踪。
2 V-CSK算法原理基于V-CSK算法的检测跟踪算法原理是利用改进的ViBe算法实现目标的检测和运动目标中心信息提取,获得检测跟踪框的4个参数,再利用CSK算法实现运动目标的跟踪。实验将基于V-CSK算法生成的检测跟踪框参数用GGT表示。综上可知,运动目标检测跟踪的实现可以分为3步骤:实现运动目标的有效检测、基于检测结果获得精准的GGT数据、将GGT传递至跟踪器实现运动目标的实时跟踪。本小节将详细介绍V-CSK算法的实现过程。
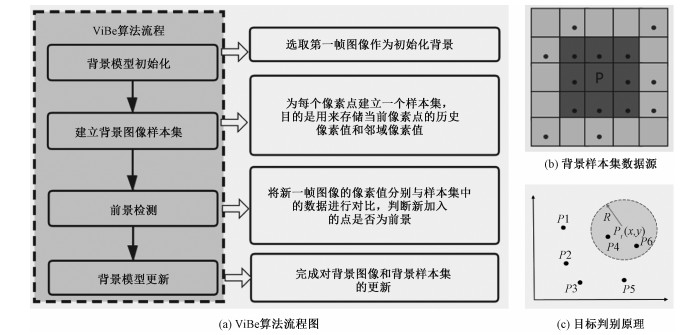
2.1 改进的ViBe算法ViBe算法是背景差分法的一种,主要用来实现运动目标检测[16],算法的关键在于如何创建稳定有效的背景模型,并适时地对背景进行更新。相比高斯建模方法、码本模型等背景差分法,具有运算速度较快、对数据可实时处理、检测准确率高等优点。
ViBe算法主要在于背景像素点的随机更新和邻域传播的思想[17]。根据每个像素和其邻域像素在空域上有相似分布,先对每个像素点建立背景样本集,计算像素点和背景样本集的像素信息相似性,从而判断下一帧该像素点属于目标还是背景,算法流程如图 2(a)。传统ViBe算法中的背景样本集选自8邻域,样本选取的范围小,若邻域范围设置过大,像素之间相似性减弱,背景样本集误差增大。针对上述问题,实验提出新的样本集选取规则,在扩大样本集选取范围的同时保证像素空间信息的相似性,并加入目标次数阈值限制减少Ghost现象。
|
Download:
|
| 图 2 ViBe算法原理介绍 Fig. 2 Introduction to the principle of ViBe algorithm | |
假设点(x, y)处的像素值大小为p(x, y),V(x, y)表示样本集数据来源区域,S(x, y)表示实际构建的背景样本集,N3(x, y), N5(x, y)表示p(x, y)的8邻域和16邻域。
总邻域为
| $ N(x, y) \in\left\{N_{3}(x, y), N_{5}(x, y)\right\}, $ | (1) |
背景样本集数据来源区域为
| $ V(x, y) \in\left\{V_{3}(x, y), V_{5}(x, y)\right\}, $ | (2) |
其中:
| $ V_{3}(x, y)=N_{3}(x, y), $ | (3) |
| $ V_{5}(x, y)=\left\{\begin{array}{ll} N_{5}(x, y), & P_{N_{5}}(x, y) \in\left[\frac{p(x, y)}{2}, \right. \\ & \left.p(x, y)+\frac{255-p(x, y)}{2}\right] \\ \text { discard, } & P_{N_{5}}(x, y) \notin\left[\frac{p(x, y)}{2}, \right. \\ & \left.p(x, y)+\frac{255-p(x, y)}{2}\right] \end{array} .\right. $ | (4) |
如图 2(b)所示,背景样本集的数据来源共有2部分,通过随机选取N个像素点,构建样本集S(x, y),当读取下一帧时,以图像(x, y)的像素值为中心,半径为R建立一个模型圆,如图 2(c)所示,圆中包含的像素点用CR(x, y)表示,即:
| $ (x, y) \in\left\{\begin{array}{ll} \text { background, } & \text { Number }\left(C_{R}(x, y) \cap\right. \\ & S(x, y))>\min \\ \text { foreground, } & \text { Number }\left(C_{R}(x, y) \cap\right. \\ & S(x, y))<\min \end{array}, \right. $ | (5) |
对点(x, y)所属类别进行判别时,需要设置2个阈值:一是像素点是否匹配的半径R; 二是背景样本集和模型圆的样本相交点数是否达标的阈值min。交集越大,表明新像素点与背景样本集越相关,新像素点为背景的可能性越大。通过改变R与min的值就可以改变该模型的灵敏度和准确度。
ViBe算法中某个像素点被判定为背景,则会以1/φ的概率从已建立的背景样本集中随机选取一个样本进行替换。在更新过程中,由于盲目更新会导致检测目标不完整,影响检测跟踪精度。因此算法采用保守更新,同时加入目标次数阈值Tforeground,当像素点连续被判为目标的次数超过阈值,从该点的背景样本集中随机选取一个样本替换该值。
2.2 目标中心信息提取算法运动目标跟踪需获取检测框信息[a, b, width, height]。实验采用多重自定义阈值滤波算法获得运动目标中心信息,通过轨迹曲线估计进行校正。同时引入人工标定和外接矩形框算法进行对比。实验将人工标定的检测框参数用GT (ground-truth) 表示,将本文算法得到检测框参数用GGT表示,以示区分。
运动目标中心信息提取算法原理如下:
1) 设置多重自定义阈值滤波器提取目标中心区域。
2) 加入噪声距离判断原则,减少噪声影响,提高目标中心区域的准确性。
3) 在目标中心区域采用中心位置均值原理估计运动目标中心点坐标。
4) 利用轨迹曲线估计对提取的目标中心预测值进行预估,同时采用插值算法对偏离轨迹的数据进行校正。
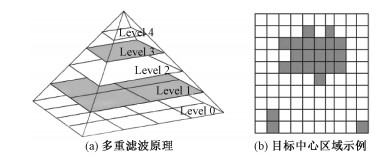
如图 3(a)所示,多重自定义阈值滤波器原理是对图像进行一次滑动卷积操作时,采用N个大小不同的滤波器处理,分别获得N个滤波结果,从中提取共同的目标中心区域,可用公式(6)表示。
| $ \text { Area }=\left(A_{1} \cap A_{2} \cap \cdots \cap A_{L}\right), \quad L \in[1, N], $ | (6) |
|
Download:
|
| 图 3 运动目标中心信息提取原理 Fig. 3 Principle of moving target center extraction | |
其中: AL表示经过第L个滤波器获得的区域,Area表示所有滤波区域交集。总滤波个数N的大小取决于运动目标的体积、外形和占比。滤波过程中通过设置阈值调节参数α确定每个滤波器的阈值Threshold。其中α和当前滤波器所占大小有关,一般Kernel越大,α越大。若采用方形滤波器,则满足Threshold=Kernel2-α。
在进行位置坐标均值操作获取前,需要对Area区域内的点进行距离判断,如图 3(b),将距离大于阈值D的点剔除,得到去噪后的中心区域Areacenter,再利用坐标均值原理,获得下一帧运动目标中心的位置
| $ \text { Area }_{\text {center }}=\left\{\begin{array}{l} \left\{(x, y)_{i, j}\right\}, & \sqrt{\left(x_{i, j}-\bar{x}_{i, j}\right)^{2}+\left(y_{i, j}-\bar{y}_{i, j}\right)^{2}}<D \\ \text { discard, } & \sqrt{\left(x_{i, j}-\bar{x}_{i, j}\right)^{2}+\left(y_{i, j}-\bar{y}_{i, j}\right)^{2}}>D \end{array}, \right. $ | (7) |
| $ \left(\bar{x}_{i, j}, \bar{y}_{i, j}\right)=\left(\frac{1}{\text {num}} \sum x_{i, j}, \frac{1}{\text {num}} \sum y_{i, j}\right), $ | (8) |
其中: xi, j∈Areacenter,yi, j∈Areacenter,num为像素个数。
得到运动目标在所有帧的预测中心位置
| $ a=\bar{x}_{i, j}-\frac{\text { width }}{2}, \quad b=\bar{y}_{i, j}-\frac{\text { height }}{2}, $ | (9) |
可获得检测框信息GGT,通过将GGT数据传递至跟踪器实现目标跟踪。
2.3 CSK算法CSK算法由Henriques等[18]提出。CSK是一种相关滤波算法,通过构造相关滤波器搜索最大响应候选区域,将该区域作为下一帧目标进行跟踪。CSK算法在MOSSE的基础上使用了核函数,同时证明核函数是循环矩阵,通过循环矩阵可以实现密集采样,并利用FFT实现快速运算。
在tracking-by-detection中,核心是分类器,训练分类器需要采集大量的正负样本。以往的采集方法大都基于目标所在区域进行随机采样,由于样本之间有冗余且迭代次数多,运算速度慢,且图像特征来源范围小。CSK算法基于整幅图像进行密集采样,不仅能够获取整个图像的特征信息,同时利用傅里叶变换快速合并所有子窗口的信息,而非迭代采样,运算速度快速提升。CSK算法是利用线性分类器进行相关滤波器的求解
| $ \min \limits_{w, b} \sum\limits_{i}^{n} L\left(\boldsymbol{y}_{i}, f\left(\boldsymbol{x}_{i}\right)\right)+\lambda\|\boldsymbol{w}\|^{2}, $ | (10) |
其中L(yi, f(xi))表示损失函数,xi和yi分别表示训练样本和标签,函数f(x)=〈w, x〉+b。CSK算法采用L(yi, f(xi))=(yi-f(xi))2作为损失函数。正则项λ‖w‖2的作用是为了防止滤波器响应过拟合现象。式(9)的闭式解为
| $ \boldsymbol{w}=\sum \nolimits_{i} \boldsymbol{\alpha}_{i} \boldsymbol{\varphi}\left(\boldsymbol{x}_{i}\right), $ | (11) |
其中: αi表示系数矢量,φ(xi)表示空间映射函数。将特征空间中的点积表达设为φT(xi)φ(x′)=k(x, x′),用核函数k代表点积运算,此时所有样本间的点积可以存储成一个核矩阵Κ,每个元素形式Κi, j=k(xi, xj)在特征空间下f(z)可写成
| $ f(\boldsymbol{z})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{z}=\sum\limits_{i=1}^{n} \boldsymbol{\alpha}_{i} k\left(\boldsymbol{z}, \boldsymbol{x}_{i}\right), $ | (12) |
由此可得
| $ \boldsymbol{\alpha}=(\boldsymbol{K}+\lambda \boldsymbol{I})^{-1} \boldsymbol{y}. $ | (13) |
根据循环核矩阵的特性可以被离散傅里叶变换对角化,可得
| $ \hat{\boldsymbol{\alpha}}=\frac{F(\boldsymbol{y})}{k^{x x x}+\lambda}, $ | (14) |
其中:函数F()表示进行傅里叶变换,xxx表示核函数如高斯核、线性核,
此时算法核心步骤为:
1) 计算循环矩阵Kgauss:通过输入的图片和目标区域,可得
| $ \begin{array}{c} \boldsymbol{K}^{\mathrm{gauss}}=\exp \left(-\frac{1}{\sigma^{2}}\left(\|\boldsymbol{x}\|^{2}+\left\|\boldsymbol{x}^{\prime}\right\|^{2}-\right.\right. \\ \left.\left.2 F^{-1}\left(F(\boldsymbol{x}) \odot F^{*}\left(\boldsymbol{x}^{\prime}\right)\right)\right)\right), \end{array} $ | (15) |
2) 更新α:
| $ \boldsymbol{\alpha}=F^{-1}\left(\frac{F(\boldsymbol{y})}{F\left(\boldsymbol{K}^{\mathrm{gauss}}\right)+\lambda}\right), $ | (16) |
3) 通过Kgauss和α计算响应值,即运动目标位置
| $ \hat{\boldsymbol{y}}=F^{-1}\left(F\left(\overline{\boldsymbol{K}^{\mathrm{gauss}}}\right) \odot F(\boldsymbol{\alpha})\right). $ | (17) |
由此可以得到与当前帧响应值最大的ŷ,该值对应的坐标就是下一帧运动目标预测位置,从而实现目标跟踪。
在V-CSK检测跟踪算法中,涉及的可调参数如表 1所示。
|
|
表 1 V-CSK算法参数含义 Table 1 Parameters meaning of V-CSK algorithm |
本文采用3组视频卫星数据进行运动目标检测跟踪实验,目标已用红框标出,3组实验数据如图 4所示。

|
Download:
|
| 图 4 本文采用的数据集介绍 Fig. 4 Introduction to the datasets used in this paper | |
第1组数据来自2016年12月发射的高分微纳卫星,轨道高度700 km,全色成像分辨率1.4 m,多光谱成像分辨率为2.8 m,视频成像宽幅20 km×5.6 km,视频帧大小2 560×1 080,视频帧数85帧,待检测跟踪目标为一架处于飞行状态的飞机。
第2组数据是墨西哥瓜达拉哈国际机场的长光卫星视频数据,视频帧大小为1 920×1 080,视频帧数68帧,待检测跟踪目标为在机场跑道滑行的飞机。
第3组数据是美国亚特兰大的长光卫星视频数据,视频帧大小为1 920×1 080,视频帧数94帧,待检测跟踪目标为一架正在空中飞行的飞机。
3.2 评价方法为了检验多重自定义阈值滤波算法对提取检测框参数的准确度,实验采用坐标偏移均值OFFSET-MEAN和均方根误差RMSE(root mean square error)表示。RMSE是观测值与真值偏差的平方和观测次数n比值的平方根,它对一组测量中特大或特小误差反映非常敏感,能很好地反映测量精度。
| $ \text { OFFSET-MEAN }=\frac{1}{n} \sum \nolimits_{i=1}^{n}\left|X_{\mathrm{obs}, i}-X_{\text {model }, i}\right| , $ | (18) |
| $ \qquad \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum \nolimits_{i=1}^{n}\left(X_{\mathrm{obs}, i}-X_{\mathrm{model}, i}\right)^{2}}. $ | (19) |
对于运动目标检测的评价指标,实验采用检测率DR(detection-rate)、虚警率FAR(false-alarm-rate)作为评价指标。
| $ \mathrm{DR} =\frac{\text { 算法检测中真实目标个数 }}{\text { 实际真实目标总个数 }}, $ | (20) |
| $ \mathrm{FAR} =\frac{\text { 虚警个数 }}{\text { 算法检测到的目标总个数 }} . $ | (21) |
对于运动目标跟踪,实验采用成功率Success和精度Precison作为评价指标,分别用成功图和精度图表示。
当某一帧的目标边框重合度OS(overlap score)大于设定的阈值时,则该帧被视为成功的,总的成功的帧占所有帧的百分比即为成功率,用成功图表示。OS的取值范围为0~1,一般阈值设定为0.5。
| $ \mathrm{OS}=\frac{\left|R_{\mathrm{GT}} \cap R_{\text {detection }}\right|}{\left|R_{\mathrm{GT}} \cup R_{\text {detection }}\right|}, $ | (22) |
其中: RGT表示GT边框,Rdetection表示预测边框, |·|表示区域的像素数目。
精度图是通过计算一系列相邻帧最大响应的坐标点(x, y)response与(a, b)GGT两者的距离在阈值范围内的帧百分比。精度图的表示方法如下
| $ \text {Precisons} =\mathrm{nnz}(\operatorname{gap}<p) / \text {numel} ( \text {gap} ), $ | (23) |
其中
| $ \operatorname{gap}=\sqrt{\sum\limits_{1}^{m}\left(x_{\text {response }}-a_{\mathrm{GGT}}\right)^{2}+\left(y_{\text {response }}-b_{\mathrm{GGT}}\right)^{2}}. $ | (24) |
在上述参数中,gap表示视频中所有帧(x, y)response和(a, b)GGT的距离总和,p表示阈值,nnz()函数表示计算矩阵中所有非零值的个数,numel()表示计算矩阵元素总个数。当(x, y)response和(a, b)GGT越接近,gap值越小,跟踪精度越趋近于1。
3.3 目标中心信息提取实验为了验证多重自定义阈值滤波算法的可行性,核心在于验证算法生成的数据GGT和实际目标的GT是否匹配。实验采用高分微纳卫星数据进行验证,原因在于视频中的目标飞机是刚体,处于直线飞行且未产生形变,减少目标本身带来的干扰,同时该卫星分辨率为1.4 m,目标尺寸清晰,角点明显,有利于构建GT数据。由于原数据尺寸为2 560×1 080,目标飞机的尺寸约为10像素×10像素,目标仅占0.003 617%,实验以目标所在的小区域作为研究范围,选取范围为480×272,目标占比为0.076 6%,提高约20倍。目标区域如图 5所示。

|
Download:
|
| 图 5 目标区域提取图(480×272) Fig. 5 Target area extraction | |
检测框数据由4个参数组成[a, b, width, height]。由于飞机外形和尺寸相对稳定,算法计算得到的宽度width和高度height变化小,对验证结果影响很小。由于目标处于运动状态,使得坐标(a, b)时刻在变化,对于验证结果影响较大,因此实验主要针对运动目标的坐标进行对比分析。实验获得3组数据,其中(a1, b1)对应实际标定的GT,(a2, b2)对应采用多重自定义阈值滤波算法得到的GGT1,(a3, b3)对应采用外接矩形框算法得到的GGT2,具体数据如表 2所示。
|
|
表 2 GT和GGT(2组)实验数据 Table 2 Experimental data of GT and GGT (two groups) |
对GT、GGT1、GGT2数据进行坐标偏移均值OFFSET-MEAN和均方根误差RMSE分析,分析结果如表 3所示。在坐标a的OFFSET-MEAN、RMSE、坐标b的OFFSET-MEAN数据中,两个对比项差别不大,但在坐标b的RMSE和(a, b)的RMSE数据中,多重自定义阈值滤波算法优于外接矩形框算法。因此可将本文的目标中心信息提取算法应用于检测跟踪实验,利用检测结果获取GGT数据,将其传至跟踪器实现后续的目标跟踪。
|
|
表 3 GT和GGT(2组)对比 Table 3 Comparison of GT and GGT (two groups) |
实验基于3组遥感视频数据进行V-CSK算法性能验证,同时增加检测算法对比实验和跟踪算法对比实验。
运动目标检测方法主要分为3大类:光流法,帧间差分法和背景差分法。光流法通过计算各个像素点随时间变化而产生的瞬时速度,得到像素点的速度特征,再利用光流场中各点的瞬时变化情况以及相邻帧之间的关联性,找到上一帧与当前帧的对应关系,从而计算出目标的运动情况实现检测。帧间差分法是利用视频中的连续两帧或连续多帧对应的像素值做差分运算,然后依据差分图像提取出运动目标。背景差分法首先进行背景模型构建,再利用当前视频帧与背景帧图像做差分运算来检测运动目标。实验根据这3个类别,选取3组对照组:LK光流法、三帧差分法和高斯背景差分法,并采用检测率DR、虚警率FAR作为评价指标。
在进行运动目标跟踪中,首先基于本文提出的目标检测和目标中心信息提取算法,获得运动目标的检测跟踪框信息,然后传递至CSK和其余9个不同跟踪算法实现性能对比。9个跟踪算法分别是CT[19]、IVT[20]、DFT[21]、ORIA[22]、ASLA[23]、L1APG[24]、MTT[25]、SCM[26]、LOT[27],同时采用成功图和精度图作为评价指标。
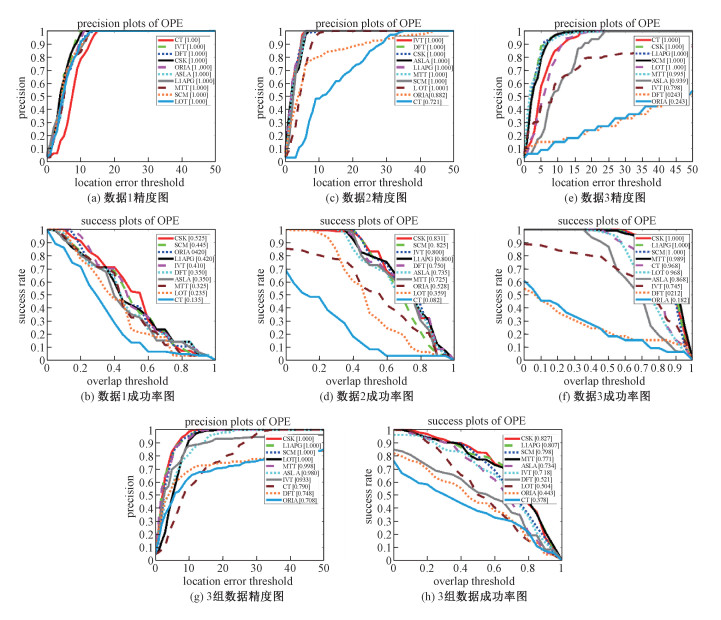
表 4展示的是不同检测算法在3个卫星视频数据集的检测结果,结果采用3位小数进行展示。图 6展示的是10个跟踪算法的性能图,在精度图中表现为低阈值高精度和在成功率图表现为高阈值高成功率则说明跟踪性能更好,同时增加横坐标阈值分别为20和0.5时的各个算法性能的图标。图 7展示的是10个跟踪算法的检测跟踪结果图,实验选取每组数据第10、20、30、40、50帧的跟踪结果进行展示。
|
|
表 4 运动目标检测结果 Table 4 Moving object detection results |
|
Download:
|
| 图 6 跟踪结果曲线图 Fig. 6 The curve of tracking results | |

|
Download:
|
| 图 7 实验结果图 Fig. 7 The plot of experimental results | |
在这3组卫星数据中,待研究的运动目标均是飞机。由上述图表可知,本文所提的检测跟踪算法在3个数据集上均能实现,检测率DR、虚警率FAR整体优于其他检测算法,在精度图和成功图均有不错表现。3组数据的检测结果见图 7(a),跟踪结果见图 7(b)~图 7(f)。
对于实验数据1,实验设置2个自定义阈值滤波器,Kernel分别为3、5,其中滤波器阈值大小分别为7、23。在图 6(a)的精度图中,所有跟踪算法的曲线变化趋势和幅度基本一致,跟踪性能没有出现特别大的差异,且无明显跟丢情况,但由图 6(b)的成功率图可知,CSK算法整体表现略优。
对于实验数据2,实验设置3个自定义阈值滤波器,Kernel分别为3、5、7。其中滤波器阈值大小分别为7、20、40。在图 6(c)的精度图中,除ORIA、CT算法,其余8种算法的精度性能均表现不错;在图 6(d)的成功率图中,CSK算法性能最优,CT算法性能最差,且为下降凹曲线;结合跟踪结果可知,CT算法在第10帧已出现跟丢情况,且跟踪框离目标越来越远,跟踪性能与曲线基本一致。
对于实验数据3,目标飞机尺寸大约为50像素×50像素,实验设置9个滤波器,Kernel分别为3、5、7、9、11、13、19、21、23。滤波器阈值Threshold大小分别为7、20、40、70、100、150、300、350、420。在跟踪性能上,CSK算法在图 6(e)的精度图和图 6(f)的成功率图上均表现良好,而DFT和ORIA算法的曲线基本吻合,与其他跟踪差距较大,两者在第20帧也出现明显跟丢现象。
图 6(g)和图 6(h)展示的是10个跟踪算法在3组数据集上的平均结果。由上述实验曲线图可知,无论是单个还是整个数据集,CSK跟踪方法均表现最优,可见基于CSK算法实现跟踪是可行的。
4 结论随着视频遥感卫星的不断发展,视频中运动目标的实时检测跟踪越来越重要。针对卫星视频运动目标,本文提出基于V-CSK算法的检测跟踪算法,在3组数据中均实现了检测跟踪,并且在检测率、虚警率、跟踪精度、跟踪成功率等指标上均有不错的表现。
| [1] |
刘韬. 国外视频卫星发展研究[J]. 国际太空, 2014, 36(9): 50-56. |
| [2] |
张过. 卫星视频处理与应用进展[J]. 应用科学学报, 2016, 34(4): 361-370. Doi:10.3969/j.issn.0255-8297.2016.04.001 |
| [3] |
朱厉洪, 回征, 任德锋, 等. 视频成像卫星发展现状与启示[J]. 卫星应用, 2015, 6(10): 23-28. |
| [4] |
何胜皎. 视频序列中运动目标检测算法的研究[D]. 兰州: 兰州理工大学, 2018.
|
| [5] |
韩露. 基于航拍图像的目标检测系统设计与实现[D]. 北京: 北京理工大学, 2015.
|
| [6] |
孟琭, 杨旭. 目标跟踪算法综述[J]. 自动化学报, 2019, 45(7): 1244-1260. |
| [7] |
葛宝义, 左宪章, 胡永江. 视觉目标跟踪方法研究综述[J]. 中国图象图形学报, 2018, 23(8): 1091-1107. |
| [8] |
袁益琴. 遥感卫星视频图像车辆动态信息提取方法研究[D]. 北京: 中国科学院大学(中国科学院遥感与数字地球研究所), 2017.
|
| [9] |
Meng L F, Kerekes J P. Object tracking using high resolution satellite imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(1): 146-152. Doi:10.1109/JSTARS.2011.2179639 |
| [10] |
吴佳奇, 张过, 汪韬阳, 等. 结合运动平滑约束与灰度特征的卫星视频点目标跟踪[J]. 测绘学报, 2017, 46(9): 1135-1146. |
| [11] |
Du B, Sun Y J, Cai S H, et al. Object tracking in satellite videos by fusing the kernel correlation filter and the three-frame-difference algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(2): 168-172. |
| [12] |
Du B, Cai S H, Wu C, et al. Object tracking in satellite videos based on a multiframe optical flow tracker[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(8): 3043-3055. Doi:10.1109/JSTARS.2019.2917703 |
| [13] |
Shao J, Du B, Wu C, et al. VCF: velocity correlation filter, towards space-borne satellite video tracking[C]//2018 IEEE International Conference on Multimedia and Expo(ICME), San Diego CA, USA: IEEE Press, 2018: 1-6.
|
| [14] |
Barnich O, Van Droogenbroeck M. ViBE: a powerful random technique to estimate the background in video sequences[C]//2019 IEEE Internationale Conference on Acoustics, Speech and Signal Processing, Taiwan, China: IEEE Press, 2009: 945-948.
|
| [15] |
Henriques J F, Caseiro R, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]//12th European Conference on Computer Vision, Florence, Italy: Springer, 2012, 7575(4): 702-715.
|
| [16] |
张文雅, 徐华中, 罗杰. 基于ViBe的复杂背景下的运动目标检测[J]. 计算机科学, 2017, 44(9): 304-307. |
| [17] |
蒋晶晶, 安博文. 低空航拍视频中基于Vibe算法的船舶检测方法[J]. 微型机与应用, 2017, 36(10): 44-47. |
| [18] |
Henriques J F, Caseivo R, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]//European Conference on Computer Vision. Berlin, Germany: Springer, 2012: 702-715.
|
| [19] |
Zhang K H, Zhang L, Yang M H. Real-time compressive tracking[C]//12th European Conference on Computer Vision, Florence, Italy: Springer, 2012, 7574(3): 864-877.
|
| [20] |
Ross D A, Lim J, Lin R S, et al. Incremental learning for robust visual tracking[J]. International Journal of Computer Vision, 2008, 77: 125-141. Doi:10.1007/s11263-007-0075-7 |
| [21] |
Sevilla-Lara L, Learned-Miller E. Distribution fields for tracking[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA: IEEE, 2012: 1910-1917.
|
| [22] |
Wu Y, Shen B, Ling H B. Online robust image alignment via iterative convex optimization[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA: IEEE, 2012: 1808-1814.
|
| [23] |
Jia X, Lu H C, Yang M H. Visual tracking via adaptive structural local sparse appearance model[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA: IEEE, 2012: 1822-1829.
|
| [24] |
Bao C L, Wu Y, Ling H B, et al. Real time robust L1 tracker using accelerated proximal gradient approach[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA: IEEE, 2012: 1830-1837.
|
| [25] |
Zhang T Z, Ghanem B, Liu S, et al. Robust visual tracking via multi-task sparse learning[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA: IEEE, 2012: 2042-2049.
|
| [26] |
Zhong W, Lu H C, Yang M H. Robust object tracking via sparsity-based collaborative model[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA: IEEE, 2012: 1838-1845.
|
| [27] |
Oron S, Bar-Hillel A, Levi D, et al. Locally orderless tracking[J]. International Journal of Computer Vision, 2015, 111(2): 213-228. Doi:10.1007/s11263-014-0740-6 |
 2021, Vol. 38
2021, Vol. 38 


