慢速目标[1-2]是指速度慢、回波信号常常淹没于强地杂波中的目标。由于回波信号本身的多普勒频率小,周围环境例如树木受风摆动产生随机多普勒分量,会造成杂波谱展宽,从而对目标检测造成不利影响。因此,对此类目标的有效探测非常重要且具有挑战性。而采用信号处理的方法对此类目标的检测不仅手段灵活,且成本较低。目前,国内外对慢速目标的检测方法主要有以下几类:基于粒子滤波的检测前跟踪(track before detect, TBD)技术的检测方法[3-4],基于变换域的检测方法,例如Radon变换[5]、Radon-分数阶Fourier变换[6]、微多普勒分析的检测方法[7-8]、多活性代理的系统检测方法[9-10]、杂声白化处理的检测方法[11]等。
基于TBD的检测方法计算量大,不利于工程实现,基于变换域的检测方法尽管计算量小和易于工程实现,但有效适用范围较窄,如田悦鑫提出的Hough方法[12]只适合一定信杂比下的小信号检测。因此,目前主流的探测雷达主要采用调频连续波(frequency-modulated continuous wave, FMCW)[13],这种体制的典型优点是可实现高精度、无距离盲区的检测,且收发系统简单、工程实现难度小、成本低。但对于慢速目标在强杂波背景下的有效检测,FMCW雷达探测仍面临以下问题[14]:1)由于不同地区的地理杂波环境不同,如何在地面强杂波环境例如树木,建筑物干扰下,有效抑制杂波,突出目标?2)对不同雷达和目标参数响应,如何实现目标检测性能的有效评估和验证?
针对以上问题,本文以FMCW雷达为研究对象,提出一种新型的自适应有限冲激响应(finite impulse response, FIR,也称抽头延迟或非递归)滤波器,并从理论、仿真和实测数据3个方面对该滤波器检测地面道路强杂波(树木、建筑物、广告牌等)干扰下的慢速目标的性能进行分析和验证。最后,分析目标检测性能的相关影响因素,为FMCW雷达检测慢速目标提供一定的借鉴意义。
1 FMCW雷达测速测距分析一般来说,FMCW雷达通过对差频信号的有效处理(如抑制环境杂波影响),获得动目标的距离、速度等信息。工业测量中,锯齿波调频连续波雷达较为常用,故以锯齿波为例。假设单个目标以速度v进行匀速直线运动,距离为R0,忽略距离-多普勒的耦合影响,FMCW雷达在快时间和慢时间维度上的差频信号表达式为
| $ S(t) = \exp \left( {\frac{{{\rm{j}}4{\rm{ \mathit{ π} }}{f_{\rm{c}}} \cdot {R_0}}}{c}} \right) \cdot \sum\limits_{l = 0}^{M - 1} {\exp } \left\{ {{\rm{j}}2{\rm{ \mathit{ π} }}\left( {\left( {\frac{{2{k_{\rm{r}}}\left( {{R_0} + vT \cdot l} \right)}}{c} + \frac{{2{f_{\rm{c}}}v}}{c}} \right) \cdot t + \frac{{2{f_{\rm{c}}}\left( {{R_0} + vT \cdot l} \right)}}{c}} \right)} \right\}, $ | (1) |
其中:fc为载波频率;kr为调频率,
通过对差频信号进行傅里叶变换估计频谱,针对距离维进行N采样,假设采样率为fs,目标距离R[15]的计算公式为
| $ R(i)=\frac{c}{2 k_{\mathrm{r}}} \frac{f_{\mathrm{s}}}{N} \cdot i, \quad i=1, 2, 3, \cdots, N. $ | (2) |
由式(2)可知,采样率fs越大,采样点数N越多,调频率kr越小(带宽越大),距离分辨率越高。若要获得速度信息,则需要对多个差频信号进行长时间积累处理(多个连续脉冲测量)。在FMCW雷达系统的信号处理中,可以通过二维傅里叶变换来获取目标的速度距离信息。目标移动速度v可以通过下式计算:
| $ v(j)=\frac{c}{2 f_{\mathrm{c}}} \frac{f_{\mathrm{PR}}}{M} \cdot j, \quad j=1, 2, 3, \cdots, M. $ | (3) |
其中,由于是调频连续波体制,脉冲重复频率fPR等于单脉冲扫频周期的倒数1/T。
与此同时,在某一确定的雷达参数下,其速度分辨率Δv为
| $ \Delta v=\frac{c}{2 f_{\mathrm{c}}} \frac{f_{\mathrm{PR}}}{M}. $ | (4) |
由式(4)可知,速度分辨率与fPR和脉冲积累个数M相关,fPR越小,M越大,速度分辨率越高。故对于近距离慢速目标的测量,其核心在于提高测速精度。
2 杂波条件下动目标检测的信号处理方法和分析实际场景中,地面的非测量目标都属于杂波,比如道路边的行道树、高大的建筑物、广告牌等,这些对于地面慢速目标来说,都是造成干扰的强杂波环境。如何有效抑制环境杂波的影响,对准确估计目标运动参数是至关重要的。因此,本节对动目标检测的信号处理方法进行理论和仿真分析,并提出抑制杂波的改善措施。
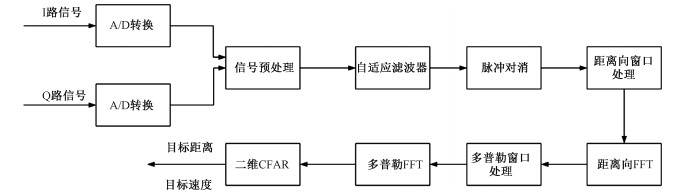
针对地面道路的目标检测情况,考虑到常见的行道树和建筑物干扰,故以幅度分布呈对数正态分布的杂波[16]为主要杂波,其在信号幅度上表现显著的尖峰值,概率密度分布的拖尾增长。针对以上环境,首先对回波信号预处理,其次杂波抑制,包括地面杂波、静止杂波和其他杂波,然后进行二维傅里叶变换[17],最后在距离多普勒图的基础上,运用二维CFAR检测方法[18]进行目标信息获取。具体信号处理流程如图 1所示。
|
Download:
|
| 图 1 信号处理流程图 Fig. 1 Flowchart of the signal processing | |
在实际应用中,不同的雷达参数和回波信号,具有不同的滤波器系数和特征频率,并且能够根据输入信号自动调整性能,进行数字信号处理的自适应滤波器研究在信号检测中是非常有意义的。
对于强杂波环境下的慢速目标而言,杂波的幅度远大于目标的幅度,对所有信号幅度求均值,可近似代表杂波的平均值。其次,将原信号减去信号均值,可以有效降低杂波高幅度的影响,进一步突显目标,表达如下:
| $ S^{\prime}(t)=S(t)-E[S(t)], $ | (5) |
| $ \beta=\frac{S(t)-E[S(t)]}{S(t)}. $ | (6) |
其中:E[S(t)]表示S(t)的统计平均,S′(t)是处理后的信号,β为幅度差值归一化数值。
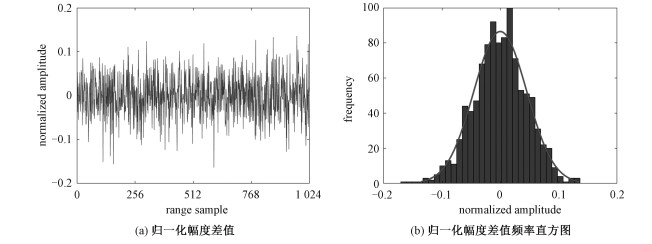
为验证上述信号处理的可行性,对有无动目标两种情况分别求均值,并按照式(6)对幅度差值做归一化比较,得到强杂波背景下的结果如图 2所示,其中总采样点数为1 024。
|
Download:
|
| 图 2 幅度差值结果分析 Fig. 2 Analysis of amplitude difference | |
从图 2(a)可看出,差值幅度归一化值β < 0.2,图 2(b)显示其值大部分集中在(-0.05, 0.05)(对应的纵坐标频次总数为总采样点数1 024),说明含有动目标和无动目标的信号幅度取均值相差不大,含有动目标情况取均值可近似等于背景杂波的均值,该结果也验证了式(5)的信号处理方法是可行且有效的。
因此,对强杂波环境下含有动目标的解调信号求均值,并进行差值计算,然后利用匹配滤波器对频域距离向进行相位压缩,消除距离向频域二次相位,压缩之后的信号S′(ς, t)如下所示:
| $ \begin{array}{c} {S^\prime }(\varsigma , t) = wa \cdot \sin c\left[ {B \cdot \left( {\zeta - \frac{{2\hat R(t)}}{c}} \right)} \right] \cdot \\ \exp \left( { - \frac{{j4{\rm{ \mathit{ π} }}\hat R(t)}}{\lambda }} \right), \end{array} $ | (7) |
其中:ς=-fς/kr,fς为信号频谱范围,wa为方位向窗口函数。
同时,压缩过信号的相位值Δφ与距离
| $ \hat R(t) = \frac{{\Delta \varphi \cdot \lambda }}{{4{\rm{ \mathit{ π} }}}}. $ | (8) |
再者,距离估计
| $ \begin{array}{c} \hat R(t) = \left( {{R_0} + {\delta _0}} \right) + \left( {{R_1} + {\delta _1}} \right)t + \left( {{R_2} + {\delta _2}} \right){t^2} + \\ \cdots \cdots O\left( {{t^n}} \right), \end{array} $ | (9) |
其中:Ri, i=1,…,n为斜距的n阶导数;δi, i=1,…,n为残余误差的n阶导数。常数部分就是雷达观测目标的最短距离R0。
一般来说,滤波器是对δ(t)部分进行减弱或消除,达到杂波抑制的效果。由于自适应滤波器的自适应性,不需要人工改变输入参数,因此常应用于实际工业领域中。但是,现今自适应滤波器[19]的应用主要是基于反馈结构来不断调整滤波器系数和频率响应。由于事先不知道噪声信号的幅度分布特点,自适应滤波器的初始值是随机值,需要不断地迭代学习从而更改滤波器系数,这样会导致信号滤波处理的时间较长。因此,基于式(5)信号处理方法,先降低环境背景杂波的影响,再根据一定规则确定自适应滤波器的初始值范围,提高滤波器的滤波速度和性能。下面是FIR滤波器的一般表达式:
| $ \boldsymbol{y}(n)=\sum\limits_{k=0}^{m-1} h(k) \cdot \boldsymbol{x}(n-k), $ | (10) |
其中:x(n)是时域上的输入信号,y(n)是输出信号,h(n)是权重系数,m是每次输出的积累数目。
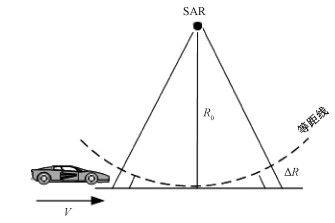
如何高效且自适应地确定权重系数h(n),从雷达探测目标的角度来看,匹配滤波器就是如何补偿距离相位,即补偿图 3所示的ΔR部分。从探测目标的角度来说,当滤波器的阈值既不淹没目标又能消除其他高频杂波时,就可以极大提高滤波器的工作效率。本文提出的滤波器改进方法是围绕探测目标的频率信息出发,将其多普勒频率估计值作为自适应滤波器的初始值,以此提高滤波器的运行效率和抑制杂波性能。
|
Download:
|
| 图 3 SAR探测目标的距离示意图 Fig. 3 Sketch of the target detection by the SAR system | |
对距离函数
根据正态分布的σ原则,为保证不遗漏目标,可取2σ或3σ原则,确保目标在检测范围内的概率达90%以上,但这会使得实际虚警概率提高。所以结合实际仿真结果分析,1σ原则保证目标能被检测概率达65%以上,且不会过多抬高虚警概率。因此,在绝大部分情况下,可以将上下浮动σ的频率值作为自适应FIR滤波器的初始值,构建权重系数
另外,自适应滤波器对整体杂波信号滤波,组合脉冲对消的方式消除零频附近静止杂波的影响,进一步突显动目标,为接下来的二维傅里叶变换和二维CFAR检测分析奠定良好的基础。
2.2 二维傅里叶变换和二维CFAR分析降低或消除环境的杂波影响后,利用二维傅里叶变换的方法快速准确得到动目标的位置。基于上述对差频信号的时域分析,式(1)经过二维傅里叶变换,得到
| $ \begin{array}{*{20}{c}} {S(a, r) = \exp \left( {{\rm{j}}4{\rm{ \mathit{ π} }}\frac{{{f_{\rm{c}}} \cdot {R_0}}}{c}} \right)\sum\limits_{l = 0}^{M - 1} {\sum\limits_{n = 0}^{N - 1} {\left\{ {\exp \left( {{\rm{j}}4{\rm{ \mathit{ π} }}\frac{{vT{f_{\rm{c}}}}}{c}l} \right) \cdot } \right.} } }\\ {\exp \left[ { - {\rm{j}}2{\rm{ \mathit{ π} }}\left( {\frac{{l \cdot r}}{{{L_Z}}} + \frac{{n \cdot a}}{{{N_Z}}}} \right)} \right] \cdot \exp [{\rm{j}}2{\rm{ \mathit{ π} }} \cdot }\\ {\left. {\left. {\left( {\frac{{2{k_{\rm{r}}}{R_0}}}{c} + \frac{{2{f_{\rm{c}}}v}}{c}} \right) \cdot \frac{T}{N} \cdot n} \right]} \right\}.} \end{array} $ | (11) |
其中:LZ,NZ分别指2D傅里叶变换的方位向和距离向数目。
通过分析式(11),二维傅里叶变换后,峰值处就是动目标的位置,即
| $ a=\left(\frac{2 k_{\mathrm{r}} R_{0}}{c}+\frac{2 f_{\mathrm{c}} v}{c}\right) \cdot \frac{T}{N} \cdot N_{Z}, $ | (12) |
| $ r=\frac{2 v f_{\mathrm{c}} T L_{Z}}{c}=f_{\mathrm{D}} \cdot T \cdot L_{Z}. $ | (13) |
由式(12)、式(13)可知,当确定峰值(a, r)的位置时,可以逆向推算出对应的速度和距离。
对多个连续脉冲的差频信号进行2D-FFT变换后,根据频谱和多普勒信息分别估计目标距离的速度。将进行2D-FFT变换后的信号记作D(R, v),二维CFAR[20]就是从|D(R, v)|,R∈[Rmin, Rmax],v∈[vmin, vmax]中检测出超过预门限的目标。其中,针对目标处于杂波环境的分布情况,适时采取单元平均CFAR,GO-CFAR,SO-CFAR或OS-CFAR方法。
检测概率一般与信杂比和门限值有关,传统意义上当且仅当周边存在噪声对目标的检测概率为
| $ P_{\mathrm{d}}=\left[1+\hat{T} Z /\left(1+R_{\mathrm{SC}}\right)\right]^{-N / 2}. $ | (14) |
其中:Pd为检测概率;
从式(14)得出,Pd反比于门限值。当强杂波淹没目标时,门限值会急剧抬高,导致目标检测概率下降。总体来说,杂波情况下,差频信号频谱的分布较复杂,不易做理论分析,接下来将通过仿真进行相关性能分析。
3 实验仿真与结果分析 3.1 场景参数针对呈对数正态分布杂波的树木、高大建筑物、广告牌等环境下的近距离慢速目标,参照锯齿形调频连续波的地基雷达(ground based-radar)实际测量慢速目标的参数设计(实测数据),设置仿真参数,如表 1所示。但是,为了比较相互之间的作用性能和目标参数,杂波参数和雷达参数可以浮动改变。
|
|
表 1 FMCW雷达仿真参数列表 Table 1 Simulation parameters for the FMCW radar |
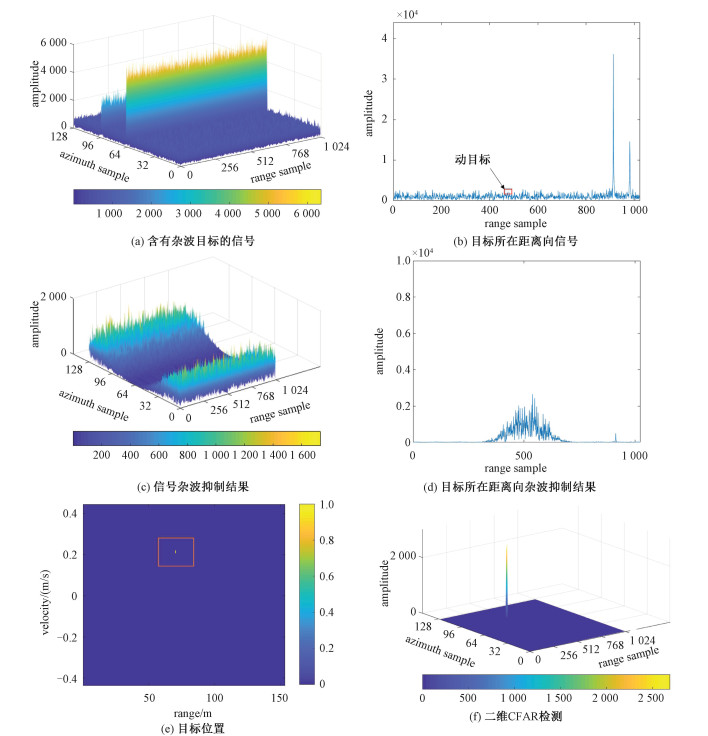
根据上述仿真参数,进行仿真实验。假设目标处于强杂波环境中,并存在多个虚假强目标的干扰(比如目标背后的高大建筑物、桥梁等),如图 4(a)、4(b)所示。按照图 1所示的信号处理流程,对信号进行杂波抑制,结果如图 4(c)、4(d)所示。随后进行二维FFT变换和二维CFAR,确定目标所在的位置,计算出目标的距离和速度,如图 4(e)、4(f)所示。
|
Download:
|
| 图 4 仿真实验目标检测结果 Fig. 4 Results of the target detection in simulated experiment | |
通过图 4(c)和4(a)的比较,可以直观地看到整体信号幅度全都降低一半,基本消除了零频附近的静止杂波。为评估滤波器的性能,定义以下几组参数,分别为:信号峰值比RP,信号均值比RA, 峰值相对误差δP,均值相对误差δA。具体表达如下:
| $ R_{\mathrm{P}}=20 \lg \left(\frac{S_{\text {peak }}^{\prime \prime}}{S_{\text {peak }}^{\prime}}\right), $ | (15) |
| $ R_{\mathrm{A}}=20 \lg \left(\frac{S_{\text {avg }}^{\prime \prime}}{S_{\text {avg }}^{\prime}}\right) , $ | (16) |
| $ \delta_{\mathrm{P}}=\frac{S_{\text {peak }}^{\prime}-S_{\text {peak }}^{\prime \prime}}{S_{\text {peak }}^{\prime}}, $ | (17) |
| $ \delta_{\mathrm{A}}=\frac{S_{\mathrm{avg}}^{\prime}-S_{\mathrm{avg}}^{\prime \prime}}{S_{\mathrm{avg}}^{\prime}}. $ | (18) |
其中:S′peak、S″peak分别为原信号和杂波抑制后的最大信号幅值;S′avg、S″avg分别为原信号和杂波抑制后的平均信号幅值。峰值比RP越小,杂波抑制效果越好,同理,均值比RA越小,抑制效果越好。
将其与现今雷达系统常用的MTI[21]脉冲对消滤波器性能相比,结果如表 2所示。
|
|
表 2 新滤波器与MTI滤波器的性能对比 Table 2 Comparison of the performance between the proposed filter and MTI filter |
峰值差值或平均值差值相对误差越大,抑制后的杂波信号幅度比原信号越小,说明抑制效果越好。由表 2得知,新滤波器信号峰值比RP=-21 dB, 均值比RA=-15.2 dB,峰值相对误差δP=91.1%,平均值相对误差δA=82.7%,与MTI脉冲对消滤波器的结果R′P=-3.6 dB,R′A=-6.6 dB,δ′P=33.4%,δ′A=53.7%相比,显然新的杂波抑制滤波器的效果更好。
图 4(e)是经过2D-FFT之后的目标位置,横纵坐标分别对应距离和速度,若速度为负数,则目标远离雷达;速度为正,则目标靠近雷达。新滤波器和MTI脉冲滤波器对目标检测结果影响如表 3所示。
|
|
表 3 新滤波器与MTI滤波器运动参数估计精度对比 Table 3 Comparison of estimated parameters between the proposed filter and MTI filter |
由表 3可知,新滤波器下的检测速度为0.199 8 m/s,距离为70.153 2 m,将其与理论值0.2 m/s、70 m比较,相对距离误差(ΔR/R)为0.2%,相对速度误差(Δv/v)为0.1%,均在10-3量级,具有良好的测量精度,相比于MTI滤波器处理下的检测精度,显示出更好的性能。同时,由图 4(f)二维CFAR的检测结果图,可以清晰地看到目标的所在位置,即杂波得到了有效抑制。
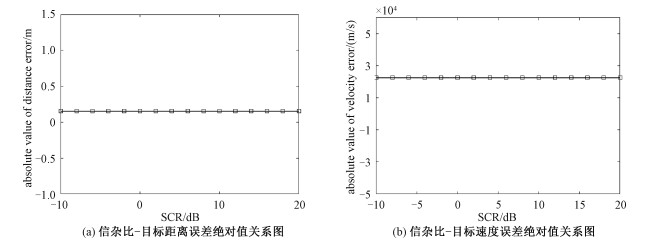
为衡量新的杂波抑制方法对目标精度检测的影响,针对不同的信杂比,观察目标的计算结果与理论值的误差大小,检测精度的变化。由图 5可知,随着信杂比的不断增加,距离和速度误差绝对值保持不变,分别约为0.153 2 m和0.000 25 m/s,这一结果显著表明新滤波器不会随着环境噪声的改变对目标检测精度产生影响,同时能够有效消除环境杂波对目标检测的影响。
|
Download:
|
| 图 5 目标检测精度影响 Fig. 5 Effects on accuracy of target detection | |
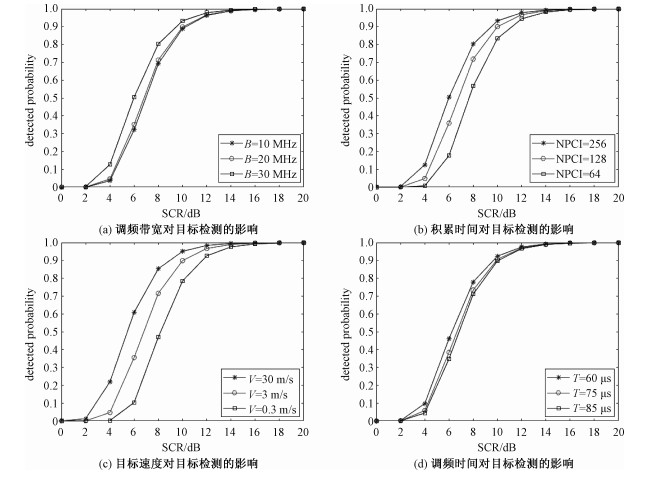
同时,为进一步探究影响目标检测性能的关键因素,下面对脉冲积累数目、调频带宽、目标速度和调频周期4种因素分别进行100次蒙特卡洛模拟。结果如图 6所示。
|
Download:
|
| 图 6 目标检测性能分析 Fig. 6 Detection performance with respect to different parameters | |
图 6反映调频带宽、脉冲累积数、目标速度以及调频时间4个因素对目标检测的影响。横坐标为信杂比,其值越大,说明信号的强度越强,反之亦成立。需要注意的是,所有对单因素影响的仿真实验都遵循控制变量的准则。
由图 6(a)看出,带宽越大,距离分辨率越高,目标之间的差异越容易被放大,检测概率越高。由图 6(b)可知,杂波的幅度越小,目标的相干积累时间越长,目标的检测概率越大。由图 6(c)可知,目标的速度越大,越容易与杂波区分,当速度小于雷达参数下的速度分辨率,则一定不能被检测出来。图 6(d)表明扫描周期越小,调频率越大,越有利于目标检测。总的来说,随着杂波强度的减弱,目标信号的强度增大,就越容易被区分。所以,为了尽可能地提高检测概率,必须同时在杂波抑制和2D-FFT中对距离维和速度维进行高分辨率处理。
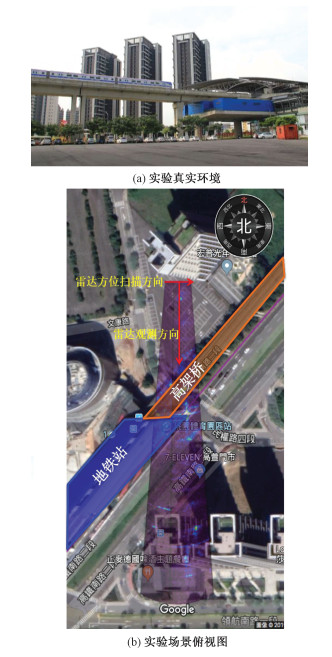
4 真实数据验证利用所提出的信号处理方法对中国台湾地区桃园市GB-SAR测试的捷运列车实验数据进行测试。该实验于2016年6月8日进行,采用起始频率为17 GHz的FMCW波形GB-SAR,对经过桃园体育馆捷运站的列车进行测量,具体的雷达参数如上述的仿真参数表 1所示。待测量的目标周围有高大的建筑物和树木,以及其他可能出现的动目标等,测量的实际环境和目标环境如图 7所示。
|
Download:
|
| 图 7 实验真实环境和俯视示意图 Fig. 7 Environment and overhead view of the experimental scenes | |
从图 7可见,列车正处于减速进站的状态中,其速度很低。由于实际测量中,有其他的动目标出现,所以以两组连续时刻同一观测场景下的数据为例,分别是第103组和第554组数据,其中第103组没有列车经过,第554组列车进站。首先分别对两组实验数据进行信号处理,然后对两组数据进行相关操作,即两组数据相乘。经相关处理后,强的信号越强,弱的信号越弱,信号最强的就是所要测量的列车目标。
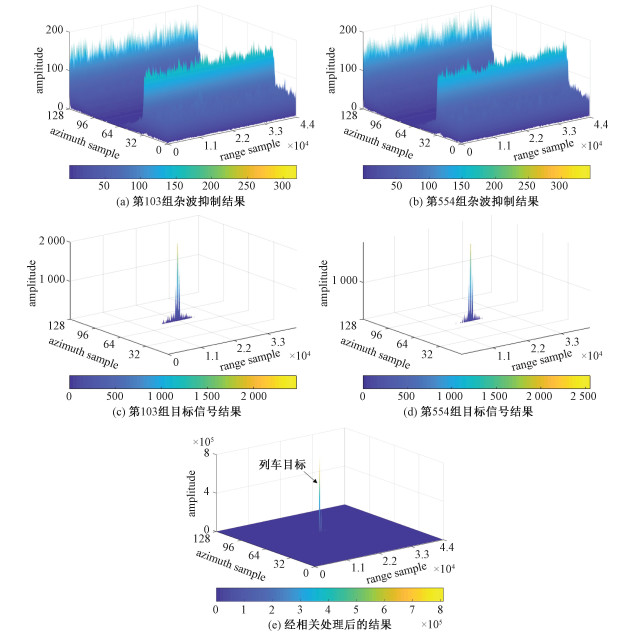
分别对第103组和第554组数据进行杂波抑制和2D-FFT等操作,结果如图 8(a)~8(d)所示,然后对两组结果进行相关处理,信号幅度最大的即为目标,如图 8(e)所示。
|
Download:
|
| 图 8 目标信号结果 Fig. 8 Results of target detection in real data | |
图 8(c)显示没有列车经过时,仍然有其他动目标存在,因此图 8(d)中不仅有列车目标,还含有图 8(c)中的动目标。为了消除列车以外的动目标影响,对两组结果进行相关操作,消除共同背景,突显目标,如图 8(e)所示,信号幅度最大的就是列车目标位置。检测的目标结果与真实测量目标的运动参数如表 4所示。
|
|
表 4 运动参数估计精度 Table 4 Estimation accuracy of motion parameters |
由表 4可知,与实际场景对比,相对距离误差为0.3%,在10-3量级范围中,具有较高的测量精度;相对速度误差为26.7%,由于实际目标正在减速进站,其径向速度接近为0,受到测量带宽1 GHz的限制,检测的速度在10-3量级,已经具有较高的精度。这也验证了带宽越大,目标越容易被检测出来的结论。因此,实测数据同样验证了该滤波器抑制的有效性,该信号处理方法能够有效应用在慢速目标检测中。
5 结论本文提出一种新型的自适应杂波抑制滤波器,并结合二维傅里叶变换技术,从理论、仿真和实测数据3个方面对该滤波器检测地面道路环境中的慢速目标的性能进行详细的分析与验证。此外还分析了与目标检测相关的影响因素包括调频带宽、积累时间、目标速度和调频时间。研究结果表明,在强杂波环境背景下,经滤波器处理后信号的峰值降低91.1%,信号平均幅度降低82.7%,相比于MTI脉冲对消滤波器的峰值降低率33.4%,平均幅度降低率55.7%,表明该新滤波器能够更好地消除峰值,更利于在强杂波中的目标提取。同时,该方法目标检测结果的相对距离误差为0.2%,相对速度误差为0.1%,均在10-3量级,优于MTI脉冲滤波器的检测精度。随后,通过蒙特卡罗模拟实验分析目标检测精度的影响因素,结果表明大带宽、长积累时间、保证不出现速度模糊的情况下,目标速度越大,调频时间越小,目标的检测概率越大,目标检测的距离速度精度越高。最后,通过GB-SAR测试的捷运列车实验数据验证,测量的相对距离误差和速度误差在10-3量级,进一步验证了该滤波器杂波抑制的有效性和目标检测的准确性。
| [1] |
李明明, 卞伟伟, 甄亚欣. 国外"低慢小"航空器防控装备发展现状分析[J]. 飞行导弹, 2017(1): 62-70. |
| [2] |
胡国平, 师俊明. 低空目标探测技术分析与展望[J]. 火力与指挥控制, 2015, 40(11): 5-9. Doi:10.3969/j.issn.1002-0640.2015.11.002 |
| [3] |
Lu J, Shui P L, Su H T. Track-before-detect method based on cost-reference particle filter in non-linear dynamic systems with unknown statistics[J]. IET Signal Processing, 2014, 8(1): 85-94. Doi:10.1049/iet-spr.2013.0117 |
| [4] |
Rutten M G, Gordon N J, Maskell S. Recursive track-before-detect with target amplitude fluctuations[J]. IEE Proceedings-Radar, Sonar and Navigation, 2005, 152(5): 345-352. Doi:10.1049/ip-rsn:20045041 |
| [5] |
陈洪猛, 李明, 卢云龙, 等. 一种时域降维多帧处理的Radon域弱目标检测[J]. 西安电子科技大学学报(自然科学版), 2017, 44(2): 14-19. |
| [6] |
Chen X, Guan J, Liu N, et al. Maneuvering target detection via Radon-fractional Fourier transform-based long-time coherent integration[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 939-953. Doi:10.1109/TSP.2013.2297682 |
| [7] |
Chen V C, Li F, Ho S-S, et al. Analysis of micro-Doppler signatures[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(4): 270-276. |
| [8] |
Villeval S, Bilik I, Gürbuz, S Z. Application of a 24 GHz FMCW automotive radar for urban target classification[C]//IEEE Radar Conference, Cincinnati, OH, USA, 2014: 1237-1240.
|
| [9] |
张云佐. 基于多活性代理的"低慢小"目标探测系统浅析[J]. 广西通信技术, 2012(2): 35-37. Doi:10.3969/j.issn.1008-3545.2012.02.009 |
| [10] |
王越, 陶然, 李炳照. 基于多活性代理的复杂信息系统研究[J]. 中国科学: 技术科学, 2008, 38(12): 2020-2037. Doi:10.3321/j.issn:1006-9275.2008.12.003 |
| [11] |
王党卫, 秦江敏, 马晓岩. 基于杂波白化处理的海面低速弱目标检测[J]. 现代雷达, 2003, 25(6): 15-18. Doi:10.3969/j.issn.1004-7859.2003.06.005 |
| [12] |
田岳鑫. Hough变换在小目标检测中的应用[J]. 激光与红外, 2008, 38(11): 1141-1143. Doi:10.3969/j.issn.1001-5078.2008.11.020 |
| [13] |
Stove A G. Erratum: linear FMCW radar techniques[J]. Radar & Signal Processing IEE Proceedings-F, 1992, 139(5): 343-350. |
| [14] |
许道明, 张宏伟. 雷达低慢小目标检测技术综述[J]. 现代防御技术, 2018, 46(1): 148-155. Doi:10.3969/j.issn.1009-086x.2018.01.024 |
| [15] |
Brooker G. Understanding millimetre wave FMCW radars[C]//Proceedings of the First International Conference on Sensing and Technology, Palmerston North, New Zealand, 2005, 152: 157.
|
| [16] |
申玉, 陶然, 单涛. 相关对数正态分布雷达杂波的建模与仿真[J]. 火控雷达技术, 2001, 30(4): 1-5. Doi:10.3969/j.issn.1008-8652.2001.04.001 |
| [17] |
Song M, Lim J, Shin D J. The velocity and range detection using the 2D-FFT scheme for automotive radars[C]//IEEE International Conference on Network Infrastructure and Digital Content. Beijing, China, 2014, 507-510.
|
| [18] |
何友, 关键, 孟祥伟. 雷达目标检测与恒虚警处理[M]. 2版. 北京: 清华大学出版社, 2011.
|
| [19] |
Diniz P S R. Adaptive filtering: algorithms and practical implementation[M]. Springer US, 2008.
|
| [20] |
Kurniawan D, Adhi P, Suryadi A, et al. Object detector on coastal surveillance radar using two-dimensional order-statistic constant-false alarm rate algorithm[J]. Telkomnika Indonesian Journal of Electrical Engineering, 2015, 12(2): 624-631. |
| [21] |
王艳霞, 张毅. 机载单天线SAR动目标检测和参数估计[J]. 中国科学院研究生院学报, 2012, 29(2): 227-233. |
 2021, Vol. 38
2021, Vol. 38 


