近年来，复合材料凭借其优良特性被广泛应用于航空航天、铁道铁路、交通运输、船舶等领域^[1-4]。已有相关研究人员对复合材料的力学性能分析方法进行了研究：孙佳伟等^[5]在探究超高韧性水泥基复合材料断裂性能时，选取3点弯曲梁作为研究对象，应用ABAQUS中扩展有限元方法分析模块，模拟分析加载条件下3点弯曲梁的裂纹扩展过程和规律; 徐世烺等^[6]基于HJC本构模型，采用分离式霍普金森杆压杆系统，对掺有聚乙烯醇纤维的超高韧性水泥基复合材料的动态压缩力学性能进行数值模拟研究，通过分析不同应变速率下材料的动态压缩应力-应变曲线讨论峰值应力动态增强因子的应变率效应，并通过LS-DYNA软件探讨破坏过程、破坏形态与应变率的关系; 林臬和张鹏冲^[7]针对复合材料层合板结构提出的以比例边界有限元为基础的正交各向异性板的数值计算模型，可适用于各种薄板与厚板的分析; 贾利勇等^[8]针对复合材料层合板三维失效分析问题建立一种基于Puck失效准则的分析模型，分别采用遍历法和分区黄金分割法的一维搜索算法预测不同应力状态下基体失效的断裂面角度; 杨万友等^[9]基于等效夹杂方法提出一种求解分布热载荷作用下复合材料温升分布场的数值分析方法，并结合共轭梯度和快速傅里叶变换提升数值分析方法效率; 惠新育等^[10]基于平纹编织SiC/SiC复合材料的制备过程和组分材料分布的多尺度特征，考虑复合材料微观结构的局部近似周期特性建立纤维丝尺度和纤维束尺度单胞模型，使用有限元分析软件对纤维丝尺度模型的弹性性能和强度性能进行预测。目前对于复合材料实际服役过程中的承载预测研究比较少，而结构件的实际服役状态对于工程安全具有重要意义，因此本文针对复合材料结构件在实际工程应用中的承载预测方法展开研究。结构件实际的服役状态是多种因素共同决定的，在力学意义上没有相关的经验公式可以对此进行预测。但长短期记忆深度学习网络模型(long short term memory，简称LSTM)具有杰出的时序信息处理能力，其独特的记忆特性使得该模型能够将前序列数据中蕴含的信息存储下来，并在后续处理中加以利用^[11-12]。因此可以用LSTM模型对已知时刻的材料服役载荷进行训练，得到未来时刻的载荷值，从而为结构件的安全评定提供依据。已有相关研究验证了LSTM模型处理时序信息的优良特性：Gers和Schtmidhuber等^[13]针对样本训练序列进行规则语言学习的研究，结果表明LSTM模型优于传统的递归神经网络; Greff等^[14]基于语音识别、手写识别和复调音乐3个任务系统分析8个LSTM模型的变体，验证了遗忘门和输出激活函数在LSTM模型中的关键作用; Alahi等^[15]构建LSTM模型来预测人体未来运动轨迹，并且在公开数据集上演示了模型性能; Turkoglu等^[16]基于LSTM网络和预先训练的CNN模型，提出一种基于LSTM的多模型预训练卷积神经网络MLP-CNNs作为植物病虫害检测的集合多数投票分类器; Qi等^[17]针对日入库流量数据的非线性和日入库流量的特点提出一种基于长短时记忆神经网络的日入库流量分解-集成学习模型，采用基于对数变换的预处理方法处理流入数据的非平稳，然后将流入数据分解，对每个分解项建立基于LSTM神经网络的回归模型得到相应的预测结果。关于LSTM模型与实际工程的结合，国内也有学者进行了研究：杨甲甲等^[18]在对电力系统的工业负荷进行短期预测时引入LSTM模型，通过数据仿真将基于LSTM模型的预测算法和已有的短期负荷预测算法结果进行对比，结果表明LSTM模型的引入能够很好地控制预测误差; 杨国田等^[19]在研究NO_X排放量时将LSTM模型与主成分分析法相结合，将主成分分析法获取到的特征作为LSTM模型的输入进行排放量预测，该研究对比LSTM模型与RNN模型的预测结果验证了LSTM模型的优良性能。因此本文也通过LSTM模型进行复合材料结构件实际服役时的受载预测，但考虑LSTM神经网络的训练效果受到数据序列长度影响^[20]，而Kalman滤波可以根据系统的观测值对系统的内部状态进行最优估计^[21-22]，因此本文将其与Kalman滤波相结合来提高预测精度。利用LSTM架构准确捕捉输入输出之间的状态转移关系，结合Kalman滤波的状态空间模型对载荷值进行预测，既可以在一定程度上克服训练数据序列长度对传统LSTM神经网络的影响，又能摆脱传统Kalman滤波对动力学模型的依赖使得模型可以从数据中学习。

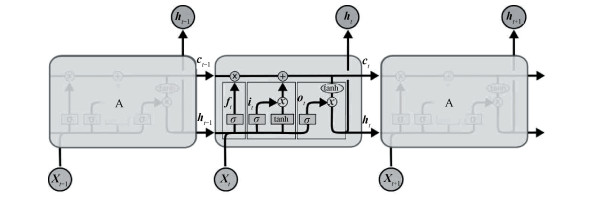
1 LSTM神经网络

LSTM网络具有杰出的时序信息处理能力，该模型能够将前序列数据中蕴含的信息存储下来，并在后续处理中加以利用。LSTM模型的结构如图 1所示，主要有遗忘门、输入门和输出门3个部分。

遗忘门结构用来筛选上一时刻的细胞状态，决定上一时刻的状态信息c_t-1有哪些要保留到当前时刻的状态信息c_t中。这一过程通过Sigmoid函数对上一时刻状态h_t-1和当前时刻输入x_t进行处理得到一个0~1之间的数值f_t，将这个权重作用到c_t-1，此结构对状态信息执行的计算可表示为

$ \boldsymbol{f}_{t}=\sigma\left(\boldsymbol{W}_{f h} \boldsymbol{h}_{t-1}+\boldsymbol{W}_{f x} \boldsymbol{x}_{t-1}+\boldsymbol{b}_{f}\right). $

(1)

输入门结构用来筛选当前时刻的输入信息，决定这些输入信息中有哪些可以存放到当前时刻的状态信息中。这一过程通过Sigmoid函数输出一个0~1之间的数值作用于当前时刻的输入信息来完成，此结构对信息执行的计算为

$ \boldsymbol{i}_{t}=\sigma\left(\boldsymbol{W}_{i h} \boldsymbol{h}_{t-1}+\boldsymbol{W}_{i x} \boldsymbol{x}_{t-1}+\boldsymbol{b}_{i}\right) . $

(2)

状态层结构主要包含σ层和tanh层两个部分：σ层用来确定将要更新的信息；tanh层用来产生候选值向量${{\mathit{\boldsymbol{\tilde C}}}_t}$加入到细胞状态中，从而完成状态信息的更新，即将C_t-1更新为C_t。状态层对信息执行的计算为

$ \widetilde{\boldsymbol{C}}_{t}=\tanh \left(\boldsymbol{W}_{c h} \boldsymbol{h}_{t-1}+\boldsymbol{W}_{c x} \boldsymbol{x}_{t}+\boldsymbol{b}_{c}\right), $

(3)

$ \boldsymbol{C}_{t}=\boldsymbol{f}_{t} \cdot \boldsymbol{C}_{t-1}+\boldsymbol{i}_{t} \cdot \widetilde{\boldsymbol{C}}_{t}. $

(4)

输出门结构用来控制信息输出，读取h_t-1和x_t，经σ函数处理输出0~1之间的数值o_t，将o_t与tanh(C_t)的乘积作为输出信息h_t。此结构能够确定哪些信息可以传递给下一个时刻，对信息执行的计算为

$ \boldsymbol{o}_{t}=\sigma\left(\boldsymbol{W}_{o h} \boldsymbol{h}_{t-1}+\boldsymbol{W}_{o x} \boldsymbol{x}_{t-1}+\boldsymbol{b}_{0}\right), $

(5)

$ \boldsymbol{h}_{t}=\boldsymbol{o}_{t} \cdot \tanh \left(\boldsymbol{C}_{t}\right). $

(6)

2 卡尔曼滤波

卡尔曼滤波的基本模型是状态空间模型，此模型描述系统内部因素的发展变化，同时也对系统内部状态和观测值之间的关联进行了表达。状态空间模型实际上是一个隐藏的马尔可夫模型，系统当前时刻的状态仅依赖于上一时刻的状态，此模型建立在系统线性和高斯白噪声的基础上。

2.1 卡尔曼滤波的状态空间模型

假设系统的状态为X_n，观测值为Y_n，下标n(n取1, 2, 3, …)表示系统所处时刻，则系统的状态空间模型为：

$ \boldsymbol{X}_{n} =\boldsymbol{A} \boldsymbol{X}_{n-1}+\boldsymbol{W}_{n}, \boldsymbol{W}_{n} \sim N(0, \boldsymbol{Q}), $

(7)

$ \boldsymbol{Y}_{n} =\boldsymbol{H} \boldsymbol{Y}_{n-1}+\boldsymbol{V}_{n}, \boldsymbol{V}_{n} \sim N(0, \boldsymbol{P}), $

(8)

其中: W_n为状态噪声，V_n为观测噪声，并且有：E(W_n)=E(V_n)=0, E(W_nW_m)=Q_nδ_mn, E(V_nV_m)=P_nδ_mn, (δ的下标m, n表示两个时刻)，在矩阵A，H，Q，P已知的前提下，卡尔曼滤波器基于最小均方误差得到n时刻系统状态的最优估计${{\mathit{\boldsymbol{\hat X}}}_n}$。

卡尔曼滤波器通过一个迭代反馈环实现最优估计，该反馈环包含两个过程：预测过程和校正过程。

2.2 卡尔曼滤波的预测过程

根据系统在n-1时刻的状态X_n-1，基于正交性原理预测n时刻系统的状态X_n，对于系统当前状态均值的估计与系统当前时刻的观测值无关：X′_n=proj_{{Y1, Y2, …，Yn-1}}X_n，“proj_{{Y1, Y2, …，Yn-1}}X_n”表示X_n在{Y₁, Y₂, …，Y_n-1}空间的投影，根据式(7)可以得到$\mathit{\boldsymbol{\hat X}}_n^\prime = \mathit{\boldsymbol{A}}pro{j_{\left\{ {{Y_1}, {Y_2}, \cdots , {Y_{n - 1}}} \right\}}}{\mathit{\boldsymbol{X}}_{n - 1}} = \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}_{n - 1}}$。

同时，得到预测误差的协方差阵$\mathit{\boldsymbol{\hat R}}_n^\prime $=E((X_n-$\mathit{\boldsymbol{\hat X}}_n^\prime $)(X_n-$\mathit{\boldsymbol{\hat X}}_n^\prime $)^T)=A${{\mathit{\boldsymbol{\hat R}}}_{n - 1}}$A^T+Q。

因此预测过程得到

$ \hat{\boldsymbol{X}}_{n}^{\prime}=\boldsymbol{A} \hat{\boldsymbol{X}}_{n-1}, $

(9)

$ \hat{\boldsymbol{R}}_{n}^{\prime}=\boldsymbol{A} \hat{\boldsymbol{R}}_{n-1} \boldsymbol{A}^{\mathrm{T}}+\boldsymbol{Q} . $

(10)

2.3 卡尔曼滤波的校正过程

计算滤波过程的卡尔曼增益K_n，利用K_n和n时刻预测误差的协方差阵$\mathit{\boldsymbol{\hat R}}_n^\prime $得到系统n时刻状态X_n的均值和协方差阵。根据n时刻系统状态均值的预测值得到状态均值$\mathit{\boldsymbol{\hat X}}_n^\prime \to {{\mathit{\boldsymbol{\hat X}}}_n}$：令Y_n=Z_n+O_n，其中O_n=proj_{{Y1, Y2, …，Yn-1}}Y_n，“proj_{{Y1, Y2, …，Yn-1}}Y_n”表示Y_n在{Y₁, Y₂, …，Y_n-1}空间的投影，Z_n是与{Y₁, Y₂, …，Y_n-1}正交的部分，称为新息。据此可以得到

$ \begin{array}{l} \hat{\boldsymbol{X}}_{n}={proj}_{\left\{Y_{1}, Y_{2}, \cdots, Y_{n}\right\}} \boldsymbol{X}_{n}\\ \ \ \ \ \ \ ={proj}_{\left\{Y_{1}, Y_{2}, \cdots, Y_{n-1}\right\}} \boldsymbol{X}_{n}+{proj}_{\left\{Z_{n}\right\}} \boldsymbol{X}_{n} \\ \ \ \ \ \ \ =\hat{\boldsymbol{X}}_{n}^{\prime}+\boldsymbol{K}_{n} \cdot \boldsymbol{Z}_{n} \\ \ \ \ \ \ \ =\hat{\boldsymbol{X}}_{n}^{\prime}+\boldsymbol{K}_{n}\left(\hat{\boldsymbol{Y}}_{n}-\boldsymbol{O}_{n}\right) \\ \ \ \ \ \ \ =\hat{\boldsymbol{X}}_{n}^{\prime}+\boldsymbol{K}_{n}\left(\hat{\boldsymbol{Y}}_{n}-\boldsymbol{H} \hat{\boldsymbol{X}}_{n}^{\prime}\right). \end{array} $

根据n时刻系统状态预测的协方差得到系统状态的协方差

$ \begin{aligned} \hat{\boldsymbol{R}}_{n} &=E\left(\left(\boldsymbol{X}_{n}-\hat{\boldsymbol{X}}_{n}\right)\left(\boldsymbol{X}_{n}-\hat{\boldsymbol{X}}_{n}\right)^{\mathrm{T}}\right) \\ &=\left(\boldsymbol{I}-\boldsymbol{K}_{n} \boldsymbol{H}\right) \hat{\boldsymbol{R}}_{n}^{\prime}\left(\boldsymbol{I}-\boldsymbol{K}_{n} \boldsymbol{H}\right)^{\mathrm{T}}+\boldsymbol{K}_{n} \boldsymbol{P} \boldsymbol{K}_{n}^{\mathrm{T}}. \end{aligned} $

计算卡尔曼增益K_n=E(X_nZ_n)(E(Z_n²))^-1=$\mathit{\boldsymbol{\hat R}}_n^\prime $H^T (H$\mathit{\boldsymbol{\hat R}}_n^\prime $H^T+ P)^-1，将卡尔曼增益K_n的表达式代入上面${{\mathit{\boldsymbol{\hat R}}}_n}$的表达式并化简得到${{\mathit{\boldsymbol{\hat R}}}_n}$=(I-K_nH)$\mathit{\boldsymbol{\hat R}}_n^\prime $。

因此校正过程得到3个关系式：

$ \boldsymbol{K}_{n}=\hat{\boldsymbol{R}}_{n}^{\prime} \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \hat{\boldsymbol{R}}_{n}^{\prime} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{P}\right)^{-1}, $

(11)

$ \hat{\boldsymbol{X}}_{n}=\hat{\boldsymbol{X}}_{n}^{\prime}+\boldsymbol{K}_{n}\left(\hat{\boldsymbol{Y}}_{n}-\boldsymbol{H} \hat{\boldsymbol{X}}_{n}^{\prime}\right) , $

(12)

$ \hat{\boldsymbol{R}}_{n}=\left(\boldsymbol{I}-\boldsymbol{K}_{n} \boldsymbol{H}\right) \hat{\boldsymbol{R}}_{n}^{\prime}. $

(13)

3 LSTM-KF模型搭建

将LSTM的信息记忆功能与Kalman滤波的预测过程相结合：将前一时刻系统状态的均值${{\mathit{\boldsymbol{\hat X}}}_{n - 1}}\;$作为LSTM的输入，通过LSTM结构的处理得到系统当前时刻状态均值的预测值$\mathit{\boldsymbol{\hat X}}_n^\prime $，之后通过对预测值进行多项式拟合得到预测误差的传递系数矩阵继而进行卡尔曼滤波。

LSTM-KF模型结构如图 2所示，其状态空间模型可表示为

$ \boldsymbol{X}_{n}=f\left(\boldsymbol{X}_{n-1}\right)+\boldsymbol{W}_{n}, \boldsymbol{W}_{n} \sim N(0, \boldsymbol{Q}), $

(14)

$ \boldsymbol{Y}_{n}=\boldsymbol{X}_{n}+\boldsymbol{V}_{n}, \boldsymbol{V}_{n} \sim N(0, \boldsymbol{P}). $

(15)

LSTM-KF模型仍然包括预测和校正两个过程，不同的是根据系统在n-1时刻的状态X_n-1来预测n时刻系统的状态X_n这一过程不再通过预先确定的模型得到，而是将前一时刻系统状态的均值${{\mathit{\boldsymbol{\hat X}}}_{n - 1}}$作为LSTM的输入，通过LSTM结构的处理得到系统当前时刻状态均值的预测值$\mathit{\boldsymbol{\hat X}}_n^\prime $，通过多项式拟合得到LSTM-KF的状态转移关系，再结合Kalman滤波结构得到n时刻系统的状态X_n，结合式(9)、式(10) LSTM-KF的预测过程表示为

$ \hat{\boldsymbol{X}}_{n}^{\prime}=f\left(\hat{\boldsymbol{X}}_{n-1}\right), $

(16)

$ \hat{\boldsymbol{R}}_{n}^{\prime}=\boldsymbol{F} \hat{\boldsymbol{R}}_{n-1} \boldsymbol{F}^{\mathrm{T}}+\boldsymbol{Q} . $

(17)

结合式(11)~式(13)LSTM-KF的校正过程表示为

$ \boldsymbol{K}_{n}=\hat{\boldsymbol{R}}_{n}^{\prime}\left(\hat{\boldsymbol{R}}_{n}^{\prime}+\boldsymbol{P}\right)^{-1}, $

(18)

$ \hat{\boldsymbol{X}}_{n}=\hat{\boldsymbol{X}}_{n}^{\prime}+\boldsymbol{K}_{n}\left(\hat{\boldsymbol{Y}}_{n}-\hat{\boldsymbol{X}}_{n}^{\prime}\right), $

(19)

$ \hat{\boldsymbol{R}}_{n}=\left(\boldsymbol{I}-\boldsymbol{K}_{n}\right) \hat{\boldsymbol{R}}_{n}^{\prime} . $

(20)

用Y_n和Ŷ_n分别表示系统n时刻的观测值与状态均值，那么损失函数可以定义为

$ L=\frac{1}{N} \sum\limits_{n=1}^{N}\left\|\boldsymbol{Y}_{n}-\hat{\boldsymbol{Y}}_{n}\right\| . $

(21)

4 LSTM-KF模型训练结果分析

针对LSTM-KF模型用MATLAB进行仿真，训练数据集选取玻璃纤维增强复合材料试件承载过程的载荷值，存取1 109个时刻的载荷值，将前80%作为训练数据去预测后20%的载荷值。

4.1 训练数据集获取

本文制备玻璃纤维增强复合材料试件，对其施加4点弯曲载荷进行训练数据集获取，试件制备原材料及试验用仪器设备如表 1所示。

本研究制备的玻璃纤维增强复合材料试件，其尺寸依据ASTM D6272—2000标准确定。预先剪裁玻璃纤维单轴布尺寸为200 mm×200 mm，每个试件铺设12层玻璃纤维单轴布，环氧树脂和环氧树脂固化剂以100:34质量比混合配置胶黏剂，对玻璃纤维复合材料层板进行真空灌注。最后按照尺寸使用切割机将制备好的玻璃纤维增强复合材料层板切割成160 mm×25 mm的试验试件，如图 3所示。

本研究在万能拉伸试验机上进行玻璃纤维增强复合材料试件的4点弯曲载荷加载试验，万能拉伸试验机选择“材料室温压缩试验”模式，采用位移控制加载，加载速率为5 mm/min。试件加载过程中利用声发射仪对试件承载信号进行采集，加载前需要将声发射传感器(频率范围为100~450 kHz，中心频率为150 kHz)均匀涂抹真空油脂并用胶带固定在试件两端，力学性能测试系统如图 4所示。

4.2 LSTM-KF模型与LSTM模型性能比较

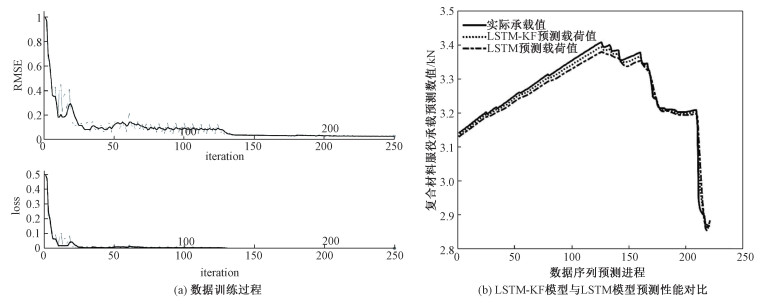
通过仿真分别得到LSTM与LSTM-KF模型的预测载荷值，将这2种模型得到的预测值与实际值作比较做出模型性能分析，如图 5所示。

从图 5(a)可以看出数据训练过程中随着数据规模的不断扩大，均方误差值以及损失函数值都呈下降趋势，最后趋近于零。分析图 5(b)中的训练曲线：LSTM-KF模型的性能优于独立的LSTM模型，LSTM-KF的预测曲线更接近后20%加载期间的实际载荷值；定量分析LSTM-KF与LSTM模型所预测的玻璃纤维增强复合材料试件承载值发现LSTM-KF模型的预测误差将LSTM模型的预测误差从0.033 kN减小到0.016 kN，降幅为51.52%。

4.3 模型稳定性分析

改变神经网络的初始参数，规定不同的神经网络隐藏单元数以及学习速率下降因子，模型性能分析如图 6和表 2、表 3所示。

图 6中4个图分别描述不同隐藏层数和不同学习速率下降因子对应的数据序列预测结果，从图中可以看出改变神经网络隐藏层数和学习速率下降因子，LSTM-KF模型对应的预测结果相互之间较为接近，其预测稳定性高于LSTM模型。结合表 2和表 3数据可以看到对应不同隐藏层数和学习速率下降因子时，LSTM-KF模型的预测性能较LSTM模型稳定提升约50%。由此验证了LSTM神经网络和Kalman滤波相结合的复合材料承载预测方法的可行性。

5 结论

本文提出一种LSTM神经网络和Kalman滤波相结合的复合材料承载预测方法，利用LSTM架构准确捕捉输入输出之间的状态转移关系，结合Kalman滤波的状态空间模型对载荷值进行预测。仿真结果表明，本文提出的预测方法表现出优良的性能：LSTM-KF模型的预测性能优于独立的LSTM，LSTM-KF的预测曲线更接近后20%加载期间的实际载荷值；定量分析LSTM-KF与LSTM所预测的玻璃纤维增强复合材料试件受力载荷值发现：LSTM-KF模型的预测误差将LSTM模型的预测误差从0.033 0 kN减小到0.016 0 kN，降幅为51.52%；对应不同隐藏层数和学习速率下降因子时，LSTM-KF模型的预测性能较LSTM模型稳定提升约50%。由此验证了LSTM神经网络和Kalman滤波相结合的复合材料承载预测方法的可行性。