2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
分形理论最早是由美国数学学家Mandelbrot首先提出来的,他把部分与整体以某种方式相似的形体称为分形,并将之用于描述具有自相似性与无标度特征的复杂系统[1-2]。20世纪90年代,Milne[3]首次将其运用于旅游景观空间结构的研究中,之后国内学者刘继生和陈彦光[4-5]从多个角度开展了对城市地理问题的研究。随着分形理论在旅游地理学中的逐渐深入,戴学军等[6-7]针对南京旅游景区景点系统空间结构进行分形特性分析,还有大量学者从旅游流规模系统[8]、旅游吸引物系统[9]、旅游地域系统[10]等多个方面也进行了空间结构分形研究。
旅游景区系统的空间结构是指一定区域内各自然和人文景区在空间上的属性和相互关系,优化的旅游景区系统既能促进旅游景区整体资源效应的发挥,在一定程度上也决定了区域基础设施和服务设施的空间分布格局。国内学者从不同地域尺度对旅游景区系统空间结构的分形特征进行了实证分析,如崔大树和孙杨[11]、刘大均等[12]通过测算聚集维数和关联维数分别分析湖州市、武汉市旅游景区系统空间结构分形特征,并提出空间优化对策;胡章鸿和段七零[13]从时空距离的视角,探讨江苏省区域景区系统的演化规律。但目前学者在围绕景区系统研究时,多集中在中东部省市,针对西部旅游景区系统的研究尤为不足。且多以4A级旅游景区为对象,系统范围较小,缺乏对其他级别景区的研究。
鉴于此,本文以西北地区重要的中心城市乌鲁木齐市为例,将其A级以上旅游景区作为研究对象,借助聚集分形模型和空间关联模型,分析乌鲁木齐市A级旅游景区系统的空间结构分形特征,以期增补分形理论在西部城市系统空间结构研究中的应用;同时基于对乌鲁木齐景区分布格局特征的分析,可为未来区域发展模式的选择以及A级旅游景区系统空间结构的优化和调整提供一定的理论指导作用。
1 研究区概况及数据来源 1.1 研究区概况乌鲁木齐,简称乌市,坐落在中国西北、新疆中部,有“亚心之都”的称号,是新疆维吾尔族自治区首府,也是中国西部地区重要的经济中心。不仅有高山冰雪、山地森林等丰富多样的旅游资源,还有种类繁多独具西域风情的民俗活动,截至2017年,全市包括5A级景区1个,4A级景区8个,3A级景区8个,2A级景区9个,构建了具有民族特色的旅游人文景观和自然风光。根据2018年新疆统计年鉴显示,乌鲁木齐市全年接待国内外游客4 624万人次,比上年增长40%;实现旅游总收入694亿元,增长54.3%,其中国际旅游收入12.98亿元,增长7%。由此可见,乌鲁木齐作为新疆重要的旅游集散地和目的地,其旅游业正处于不断上升的发展阶段。
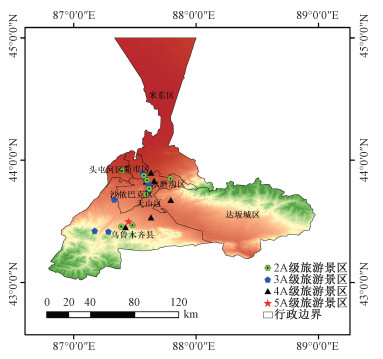
1.2 数据来源以乌鲁木齐市行政区范围为研究区域,根据乌鲁木齐市人民政府网(http://www.urumqi.gov.cn)2017年公布的《乌鲁木齐市A级旅游景区信息》,获取到乌鲁木齐市26个A级景区有效样本点。通过百度地图拾取坐标系统获取各景区地理坐标,运用ArcGIS10.2在矢量化地图上,对乌鲁木齐市A级旅游景区的空间分布进行可视化表达(如图 1)。鉴于天山大峡谷是A级旅游景区系统中级别最高、影响力最强的唯一一个5 A级景区,因此在数据处理过程中,将其作为中心景区测算其聚集维数与空间关联维数,并以此分析整个系统的空间结构分形特征。
|
Download:
|
| 图 1 2017年乌鲁木齐市A级旅游景区空间分布图 Fig. 1 Spatial distribution of the class-A tourist attraction in Urumqi in 2017 | |
Mandelbrot[14]首次提出分形的概念,并指明分形具有自相似性和标度不变性两个重要特征,也就是系统的某种结构或过程从不同的空间尺度或者时间尺度来看都是相似的。这种局部形态和整体形态的相似可以是完全相同,也可以是统计意义上的相似,因此常用分维作为分形的定量表征和基本参数[15]。在系统空间结构的研究方面,常用聚集维数与关联维数两种分维进行分析。
2.1 聚集维数测算模型假设旅游景区系统内各景区按照某种自相似规则围绕中心景区呈现凝聚态分布,且回转半径R与该系统的总半径呈线性比例,即分形体是各向均匀变化的,同时不考虑边界效应,该旅游景区系统不是一个几何上的多重分形。可借助几何测度的关系确定半径为r的圆周内的测算点数目N(r)与相应半径的关系[4]
| $ N(r) \propto {r^{{D_f}}}, $ | (1) |
式中: Df为分维,且如果假设正确,则可利用回转半径法测算系统空间聚集的分维数。由于半径r的单位取值会影响到分维数值,可将其转换为平均半径进行计算,平均半径定义为
| $ {R_s} = {\left( {\frac{1}{S}\sum\limits_{i = 1}^n {{r_i}^2} } \right)^{\frac{1}{2}}}. $ | (2) |
则一般分维关系可表示为
| $ {R_s} \propto {S^{\frac{1}{D}}}, $ | (3) |
转化为对数线性形式可得
| $ \ln {R_s} = \frac{1}{D}\ln S + A. $ | (4) |
式中: Rs为平均半径,ri为第i个景区到中心景区的欧式距离,A为常数。由于D反映的是各景区到中心景区随机聚集的特征,故称为聚集维数。将(S, Rs)绘制成双对数坐标图,通过最小二乘法可求出分维值。
聚集维数反映的是旅游景区系统内各旅游景区以中心景区为核心的空间聚集程度,即各景区分布从中心景区向周围腹地的密度衰减特征[6]。当聚集维数D < 2时,旅游景区系统的景区空间分布密度是从中心向周边逐渐衰减的;当D=2时,旅游景区系统的景区空间分布密度从中心向周边是均匀的;当D>2时,旅游景区系统的景区空间分布密度从中心向周边逐渐增大,这种离散状态属于非正常情况。
2.2 关联维数测算模型客观上来说,旅游景区系统内各景区之间的分布存在一定的空间相关性[16],可将旅游景区系统的空间关联模型表示为
| $ C(r)=\frac{1}{N^{2}} \sum \nolimits_{i}^{N} \sum \nolimits_{j}^{N} \theta\left(r-d_{i j}\right)(i \neq j), $ | (5) |
式中:N为系统内景区数目,r为给定的距离标度尺码,dij为i、j两个景区之间的欧式距离也称乌鸦距离。另外,θ为Heaviside跃阶函数,满足
| $ \theta\left(r-d_{i j}\right)=\left\{\begin{array}{ll} 1, & \text { 当 } d_{i j} \leqslant r \text { 时 } \\ 0, & \text { 当 } d_{i j}>r \text { 时 } \end{array} .\right. $ | (6) |
如果旅游景区系统的空间分布是分形的,则应具有标度不变性,即
| $ C(\lambda r) \propto \lambda^{D^{\prime}} C(r), $ | (7) |
| $ C(r) \propto r^{D^{\prime}}. $ | (8) |
转化为对数线性形式可得
| $ \ln C(r)=D^{\prime} \ln r+B. $ | (9) |
式中: D′即为空间关联维数也称为乌鸦维数,B为常数。
就表征空间分布而言,空间关联维数反映旅游景区系统要素空间分布的均衡[7]。一般情况下,其数值介于0~2,当D′→0时,表明景区分布高度集中于中心景区;当D′→2时,表明景区的空间分布很均匀。另外,关联维数还能反映旅游景区系统内各景区之间的交通网络通达性。通过把式(5)中的dij改为景区间的实际距离,也称为乳牛距离,同理计算得到交通网络的关联维数D″,也称为乳牛维数。由此可得牛鸦维数比为
| $ \rho = D''/D'. $ | (10) |
若牛鸦比值ρ < 0.5,表明景区之间的交通通达性较差;若0.5≤ρ < 1,表明景区之间通达性较好[17]。即越接近于1,表示景区之间交通网络通达性越好,关联度越高。
3 结果分析 3.1 旅游景区系统空间结构聚集维数分析选取乌鲁木齐市A级旅游景区26个,并以质量最高、影响力最大的5A级景区天山大峡谷为中心景区进行聚集维数测算。通过百度地图坐标拾取器对每个景区精确定位并获取其经纬度,利用ArcGIS10.2空间分析工具处理得到各景区到天山大峡谷的欧式距离,并将其转化为平均半径(表 1),最后把(S, Rs)进行拟合得到模型,绘制成双对数散点图(图 2)。
|
|
表 1 乌鲁木齐市A级旅游景区系统聚集维数测算数据 Table 1 Calculation data of aggregation dimension of the class-A tourist attraction system in Urumqi |
|
Download:
|
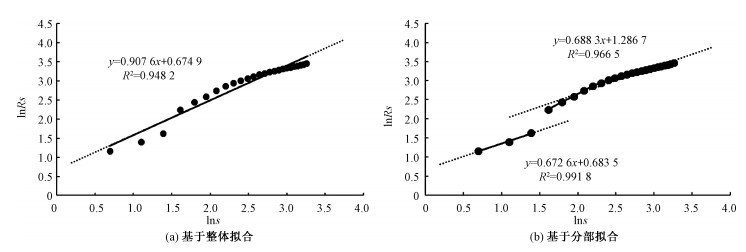
| 图 2 乌鲁木齐市A级旅游景区系统聚集维数双对数图 Fig. 2 Double logarithm of aggregation dimension of the class-A tourist attraction system in Urumqi | |
本文以天山大峡谷为测算中心的拟合模型为lnRs=0.908lns+0.675,判定系数R2=0.948。由此可知聚集维数D=1.102 < 2。这表明乌鲁木齐市A级旅游景区系统中心景区吸附作用较强,空间结构上呈现聚集分布。但由于吸附半径有限,整体空间分布密度由中心向四周衰减较快,即景区在空间布局中越往外围分布越集中, 且不同方向上的集中性程度不同,在演变过程中可能出现多中心并存的格局。
在图 2的散点图中,拟合的曲线存在明显的两段式形态,即存在2个数值不一的无标度区,范围分别在0.693~1.386、1.609~3.258。这说明在以天山大峡谷为中心景区时,旅游景区系统演化过程中有显著的双分形结构,在不同的空间尺度呈现出不同的有序组织结构[18]。第1个无标度区拟合模型为lnRs=0.673lns+0.684,判定系数R2=0.992,由此可知聚集维数为1.487,表明景区从银都度假区向华联现代农业科技示范园等周边景区密度衰减较慢。第2个无标度区拟合模型为lnRs=0.688lns+1.287,判定系数R2=0.967,易得聚集维数为1.453,在此区间内景区空间分布较为集中,主要是城市核心区的休闲娱乐性景区。第2个无标度区间的聚集维数小于第1个无标度区间,且在距离中心景区5 km(即拐点)以外的范围聚集了系统内26个景区的22个,可见距离中心5 km以内的旅游景区从中心向四周衰减的速度与效果都低于5 km外的旅游景区。
3.2 旅游景区系统空间结构关联维数分析利用ArcGIS10.2邻近距离分析工具,计算乌鲁木齐市A级旅游景区系统内各景区之间的欧式距离,获得26×26距离矩阵。根据景区之间的距离范围,令步长为5 km,利用上述公式,在r取值不同情况下,计算得出一系列不同的C(r)值(表 2),并将(r, C(r))进行拟合,绘制出双对数散点图(图 3)。
|
|
表 2 乌鲁木齐市A级旅游景区系统乌鸦维数测算数据 Table 2 Calculation data of crow dimension of the class-A tourist attraction system in Urumqi |

|
Download:
|
| 图 3 乌鲁木齐市A级旅游景区系统乌鸦维数双对数图 Fig. 3 Double logarithm of crow dimension of the class-A tourist attraction system in Urumqi | |
由图 3可以看出,整个旅游景区系统拟合模型为lnC(r)=0.713lnr-2.966,判定系数R2=0.977,可知乌鸦维数D′为0.713(介于0~1)。这一方面说明旅游景区系统有显著的分形特征,具有空间自组织优化趋势;另一方面也说明天山大峡谷为中心各景区分布较集中,关联程度较高,各景区之间联系密切。
在拟合模型中,存在2个明显的无标度区间,拐点位于lnr=4.007处,即r=55 km时。得到第1个无标度区间拟合模型为lnC(r)=0.781lnr-3.154,判定系数R2=0.990;第2个无标度区间拟合模型为lnC(r)=0.072lnr-0.312,判定系数R2=0.894。2个无标度区间的乌鸦维数D′1、D′2分别为0.781、0.072,且两者差异较大、后者更接近于0,比较之下,第2段区间内景区分布的集中性程度更高,相互关联性更大,空间结构的分布更紧凑,对各小景区而言更易整合形成大规模集群的旅游景区。第1个无标度区间范围在1.609~4.007,第2个无标度区间范围在4.094~4.382,很明显第1个区间范围跨度远大于第2个区间,这表明大部分旅游景区在以天山大峡谷为中心空间优化发育程度相对较好, 且在交通干线附近分布比较均衡。
同样,将各景区之间的欧式距离换成各景区之间的乳牛距离,即实际交通距离,取步长为5 km,改变不同的r值, 同样得到系列C(r)值(表 3),并将(r, C(r))绘制成点对双对数散点图(图 4)。基于乳牛距离拟合得到的模型为lnC(r)=0.788lnr-3.379,判定系数为R2=0.975。同理测算乳牛距离分维值为D″=0.788,进一步表明乌鲁木齐市A级旅游景区的空间结构存在分形特征,且景区的空间分布较为集中。最后得到乌鸦维数与乳牛维数的比值即牛鸦比值ρ=1.105>1,可知乌鲁木齐市旅游景区之间的公路交通网络体系还不够完善,总体连通性一般。
|
|
表 3 乌鲁木齐市A级旅游景区系统乳牛维数测算数据 Table 3 Calculation data of cow dimension of the class-A tourist attraction system in Urumqi |

|
Download:
|
| 图 4 乌鲁木齐市A级旅游景区系统乳牛维数双对数图 Fig. 4 Double logarithm of cow dimension of the class-A tourist attraction system in Urumqi | |
本文基于分形理论,对乌鲁木齐市A级旅游景区系统空间结构的聚集维数和关联维数进行测算,揭示研究区A级旅游景区分布规律及其空间结构分形特征。通过结果分析,得出以下结论:
1) 构建知名旅游目的地,采取多中心协同发展模式
根据以天山大峡谷为中心景区对聚集维数的测算结果可看出,乌鲁木齐市旅游景区系统空间结构呈现聚集分布,中心景区对其他各景区存在吸附作用。系统整体存在明显的双分形结构,2个无标度区间以5 km作为分界点,都呈现以各自中心景区为聚集点的分形聚集特征。第1个区间的旅游景区从中心向四周衰减的速度与效果都低于第2个区间,且第1个区间内的景区类型主要是城市郊区型度假村,第2个区间是城市核心区的休闲娱乐性景区,两者类型的差异会使得系统演化过程中极易出现多个中心并存的格局。因此,在乌鲁木齐市未来旅游规划中,可建议采取多中心协同发展模式,极力打造多个集聚中心,构建知名旅游目的地,增强每个中心对周边景区的吸附力,形成一系列景区组团区域,以带动A级旅游景区的共同发展。
2) 大力发展主题式景区,加强景区资源的整合
以天山大峡谷为中心景区测算的乌鸦维数双对数图基本呈线性分布,且存在显著的双分形特征。旅游景区系统内各景区之间表现出较强的关联度,空间结构整体自组织优化趋势明显,不同标度区间也表现出不同的有序结构。在标度区间跨度大的范围,各景区围绕交通干线分布均衡,相互之间联系紧密;在跨度小的范围内,各景区空间分布集中、结构紧凑,自组织优化能力更强。乳牛维数其双对数图也呈现线性分布,具有明显的单分形结构。从数值上看,与理论上呈现的景区分布比较一致,各景区之间在空间上分布比较集中,空间关联性较好。因此,应该在充分发挥景区集聚优势的基础上,大力打造主题式如度假型、观光型、娱乐型等景区组团发展,加强景区之间的资源整合,提升景区知名度。
3) 打造精品自驾游路线,形成旅游空间网络体系
从牛鸦比值来看,其值大于1,即乳牛维数大于乌鸦维数,这表明旅游景区系统内整体交通网络还不尽完善,交通网络通达性一般。完善的交通网络不仅有利于旅游景区客流交流,同时,交通网络的优化还能促进新的旅游景区的产生以及旅游景区整体资源的互补;旅游景区作为交通网络上的节点,它的产生与发展同样也影响交通网络的布局规划,对交通功能的发挥也起着举足轻重的作用。在未来的发展过程中,更应完善交通网络体系,挖掘交通优势,加强景区之间旅游交通建设。并打造精品自驾游路线,促进不同类型旅游景区之间的交流,加快大规模多层次的旅游空间网络体系的形成,从而增强旅游景区系统的对外吸引力。
4.2 讨论在分形理论的基础上,聚集维数从密度分布的角度描述了以中心景区为核心呈现的聚集状态;关联维数根据景区间距离表征空间相关性强弱,利用两者反映的不同分布特征可以较好地分析旅游景区系统空间结构。这一方面增加了分形理论在空间特征分析方面的运用,另一方面也分析了乌鲁木齐市A级旅游景区整体分布格局,揭示了景区和交通网络之间相互关联的内在规律,可在未来交通基础设施的布置以及旅游整体结构规划、旅游线路设计和景区开发建设等方面提供参考作用。分形理论日渐成熟,用于系统整体空间结构的研究也更加深入,但文章目前在系统中心景区选择上还有局限性;另外,对其时间序列上的动态演化进行研究可能对反映其空间结构优化的过程意义深刻,具有较好的研究前景,在未来的研究中有待进一步挖掘。
| [1] |
Mandelbrot B B. The fractal geometry of nature[M]. New York: W H Freeman, 1982.
|
| [2] |
Bölviken B, Stokke P R, Feder J, et al. The fractal nature of geochemical landscapes[J]. Journal of Geochemical Exploration, 1992, 43(2): 91-109. Doi:10.1016/0375-6742(92)90001-O |
| [3] |
Milne B T. Measuring the fractal geometry of landscapes[J]. Applied Mathematics and Computation, 1988, 27(1): 67-79. Doi:10.1016/0096-3003(88)90099-9 |
| [4] |
刘继生, 陈彦光. 城镇体系空间结构的分形维数及其测算方法[J]. 地理研究, 1999, 18(2): 171-178. Doi:10.3321/j.issn:1000-0585.1999.02.009 |
| [5] |
陈彦光, 刘继生. 城市土地利用结构和形态的定量描述: 从信息熵到分数维[J]. 地理研究, 2001, 20(2): 146-152. Doi:10.3321/j.issn:1000-0585.2001.02.003 |
| [6] |
戴学军, 丁登山, 许志晖, 等. 旅游景区(点)系统空间结构随机聚集分形研究: 以南京市旅游景区(点)系统为例[J]. 自然资源学报, 2005, 20(5): 706-713. Doi:10.3321/j.issn:1000-3037.2005.05.010 |
| [7] |
戴学军, 丁登山. 旅游景区(点)系统空间结构关联维数分形研究: 以南京市景区(点)系统为例[J]. 资源科学, 2006, 28(1): 180-185. Doi:10.3321/j.issn:1007-7588.2006.01.029 |
| [8] |
贺晓慧, 白凯, 卫海燕, 等. 西安特殊时段旅游流规模分形结构特征研究: 以"十一"黄金周为例[J]. 干旱区地理, 2011, 34(5): 858-865. |
| [9] |
李玏, 刘家明, 宋涛, 等. 基于聚集分形维数的旅游吸引物空间结构特征研究: 以北京市为例[J]. 干旱区资源与环境, 2016, 30(5): 197-202. |
| [10] |
宋涛, 陈雪婷, 陈才. 基于聚集分形维数的旅游地域系统空间优化研究[J]. 干旱区资源与环境, 2017, 31(4): 189-194. |
| [11] |
崔大树, 孙杨. 基于分形维数的湖州旅游景区系统空间结构优化研究[J]. 地理科学, 2011, 31(3): 337-343. |
| [12] |
刘大均, 谢双玉, 陈君子, 等. 基于分形理论的区域旅游景区系统空间结构演化模式研究: 以武汉市为例[J]. 经济地理, 2013, 33(4): 155-160. |
| [13] |
胡章鸿, 段七零. 基于时空距离的江苏省景区系统聚集分形演化研究[J]. 长江流域资源与环境, 2014, 23(9): 1208-1214. Doi:10.11870/cjlyzyyhj201409004 |
| [14] |
Mandelbrot B B. Hong long is the coast of Britain? Statistical self-similarity and fractional dimension[J]. Science, 1967, 156: 636-638. Doi:10.1126/science.156.3775.636 |
| [15] |
陈勇, 艾南山. 城市结构的分形研究[J]. 地理学与国土研究, 1994, 10(4): 35-41. |
| [16] |
谢天成, 覃平, 谢正观. 环北部湾经济圈城镇体系结构及其分形模型研究[J]. 中国科学院研究生院学报, 2008, 25(2): 185-191. |
| [17] |
梁发超, 刘诗苑, 刘黎明. 基于分形理论的乡村聚落景观空间特征及演变: 以厦门市为例[J]. 应用生态学报, 2017, 28(8): 2640-2648. |
| [18] |
芮旸, 马滕, 王兴, 等. 山地城市旅游景区空间结构分形研究: 以安康市为例[J]. 山地学报, 2018, 36(4): 607-616. |
 2021, Vol. 38
2021, Vol. 38 


