悬浮颗粒污染物如PM2.5、PM10等对于大气环境和人类健康有着不可忽视的危害作用[1-3],因此是工业生产中重点控制的污染源之一。但近年来最新的研究发现尺寸更小也更容易被忽略的纳米尺寸(小于500 nm)的颗粒污染物相对大颗粒而言能对人体的呼吸系统、心肺功能产生更为严重的影响[4-5]。而工业中所使用的除尘设备如静电除尘器(electrostatic precipitator, ESP)等对于纳米颗粒的控制效果较差,且人们对于纳米尺寸的颗粒在ESP中的运动、荷电特性认识不足,缺乏足够的理论指导,这对提高ESP中纳米颗粒的脱除效率来说是十分不利的。
ESP是目前燃煤电厂运用最多的高效除尘设备之一,其基本原理是通过电极高压放电使空气电离,让粉尘颗粒荷电从而在电场力作用下附着到集尘板上[6]。由于静电除尘本身是一个较为复杂的多场耦合的气固两相流问题,特别是考虑到颗粒迁移和电动力(electrohydrodynamic, EHD)效应的影响,而纳米颗粒相对于微米与亚微米颗粒而言,其受力和荷电特性都会发生相应的变化,最终呈现的捕集效率的变化也是十分特殊的,而目前相关的较为深入的研究还较少。Saradari等[7]和Li与Ahmadi[8]研究纳米颗粒在均匀电场中的沉积与扩散特性,并分别考虑层流与湍流两种流态,最终获得5~200 nm大小区间的纳米颗粒运动特性。但遗憾的是该研究并没有考虑不均匀电场和电晕放电情况下的纳米颗粒运动,也没有对颗粒的受力和微观运动状况进行深入的分析。毕文剑等[9]研究高温ESP中的颗粒运动特性,也深入研究了颗粒的受力状况和荷电历程,但所研究的颗粒尺寸未涵盖纳米颗粒。Huang和Chen[10]利用实验方法研究单区干式ESP中100 nm以下纳米颗粒的穿透效率与粒径的关系,发现除尘效率与颗粒尺寸的关系曲线会出现一个U型转折,但并没有深入地分析其机理。Lin和Tsai[11]建立预测纳米颗粒在2-D ESP中捕集效率的数学模型,并与Huang和Chen[10]的实验数据进行对比,发现两者能够在大部分区域较好地吻合,但由于未考虑颗粒荷电效应对于电场的影响,在颗粒尺寸较小时高估了除尘效率。总的来说,前人的研究都没有深入探及ESP的不均匀电场中纳米颗粒的运动荷电特性,并分析这些特性对于除尘效率的综合影响,且颗粒的荷电效应对电场的影响也通常被忽略。而在本研究中,其被证明是影响纳米颗粒除尘效率的重要因素之一。
针对此研究现状,本文建立实验室尺寸2D干式ESP中的耦合电场及颗粒运动的多场数值模型,着重研究在ESP中纳米颗粒的运动及其荷电特性,包括纳米颗粒的粒径、颗粒荷电等因素对于纳米颗粒在ESP中的受力、沉积和荷电过程的影响,不仅关注宏观上纳米颗粒脱除效率的变化,更从微观角度详细探究纳米颗粒独特的运动荷电特性。这为提高ESP对于纳米颗粒的捕集效率提供了理论指导,对于进一步降低工业生产造成的微细粉尘对于环境和人体健康的影响有着一定的积极作用。
1 数值方法本文建立ESP内部的包含流场、电晕电场、离子密度场、颗粒荷电模型的多场耦合数理模型,由商业软件ANSYS FLUENT实现对网格的处理及运算,通过其二次开发功能用户自定义函数(user defined function, UDF)和用户自定义标量(user defined scalar, UDS)建立统一的对流扩散方程,从而计算得到ESP内电场及离子密度分布。对于纳米颗粒的运动,采用拉格朗日方法对颗粒的轨迹进行追踪(考虑库仑力、曳力及布朗力),颗粒的荷电速率利用Lawless和Sparks[12]提出的综合荷电方程来计算。
1.1 气相控制方程在工业ESP中,由于离子风效应的干扰,绝大多数ESP内的流场处于紊流状态,只有少数双区ESP能达到接近层流状态[13]。因此,本文采用雷诺时均湍流模型(Reynolds averaged Navior-Stokes model, RANS)对ESP内的流场进行数值模拟。对于稳态湍流,控制方程如下:
质量守恒方程
| $ \frac{\partial}{\partial x_{i}}\left(\rho u_{i}\right)=0, $ | (1) |
动量守恒方程
| $ \begin{array}{c} \frac{\partial}{\partial x_{j}}\left[\rho u_{i} u_{j}-\left(\mu+\mu_{\mathrm{t}}\right) \frac{\partial u_{i}}{\partial x_{j}}\right]=-\frac{\partial p}{\partial x_{i}}+ \\ f_{\mathrm{D} i}+\left(\rho_{\mathrm{ion}}+\rho_{\mathrm{pc}}\right) E_{i}, \end{array} $ | (2) |
式中:ui是流体速度在xi方向的分量;μt是湍流黏性系数;fDi是颗粒对流体造成的的曳力;ρion, ρpc分别代表离子电荷密度和颗粒电荷密度,二者之和即为空间电荷密度;Ei是电场强度分量,(ρion+ρpc)Ei项代表电场对流场产生的离子风效应。
1.2 电场控制方程在干式ESP中,电晕产生的电场可用泊松方程和电流连续性方程表示,如式(3)、式(4)所示。
泊松方程
| $ \frac{\partial^{2} \varphi}{\partial x_{i}{}^{2}}=-\frac{\rho_{\mathrm{ion}}+\rho_{\mathrm{pc}}}{\varepsilon_{0}}, $ | (3) |
电流连续性方程
| $ \frac{\partial}{\partial x_{i}}\left[\rho_{\mathrm{ion}}\left(k_{\mathrm{ion}} E_{i}+u_{i}\right)-D_{\mathrm{e}} \frac{\partial \rho_{\mathrm{ion}}}{\partial x_{i}}\right]=0, $ | (4) |
| $ E_{i}=-\frac{\partial \varphi}{\partial x_{i}}. $ | (5) |
泊松方程和电流连续性方程均可用如下统一的输运方程进行表述:
| $ \frac{\partial}{\partial x_{i}}\left(F_{i} \varPhi-\varGamma_{\varPhi} \frac{\partial \varPhi}{\partial x_{i}}\right)=S_{\varPhi}, $ | (6) |
其中:φ为电势;ε0为真空介电常数;kion为离子迁移率;Ek为场强在xk方向上的分量;De为离子的有效扩散系数;ρpc是颗粒的荷电密度,在本文研究中被证明对于电晕放电和颗粒沉积有着重要的影响,因此不能如许多文献一般将其忽略,在这里其作为源项加入泊松方程中。扩散项、对流项、源项如表 1所示。
|
|
表 1 电势、离子电荷密度的标量输运方程对应项 Table 1 Terms of the scalar transport equations of electric potential, charge density |
颗粒在电晕场中运动时会带上一定的电量,荷电机制主要分为电场荷电与扩散荷电。粒子的荷电量决定了颗粒所受静电力的大小从而影响到颗粒的运动。Long和Yao[14]指出,Lawless和Sparks[12]提出的综合荷电率模型能够较为准确地计算颗粒在运动过程中的总荷电量:
| $ \frac{{{\rm{d}}{q_{\rm{p}}}}}{{{\rm{d}}t}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{q_{\rm{s}}}}}{\tau }{{\left( {1 - \frac{q}{{{q_{\rm{s}}}}}} \right)}^2} + \frac{{2{\rm{ \mathit{ π} }}\alpha \rho {k_{{\rm{ion}}}}{k_{\rm{B}}}{d_{\rm{p}}}}}{{\rm{e}}}, }&{q < {q_{\rm{s}}}}\\ {\frac{\alpha }{{4\tau }}\left( {q - {q_{\rm{s}}}} \right)\exp \left( {\frac{{{\rm{e}}\left( {{q_{\rm{s}}} - q} \right)}}{{2{\rm{ \mathit{ π} }}{\varepsilon _0}{k_{{\rm{ion}}}}{k_{\rm{B}}}T{d_{\rm{p}}}}}} \right), }&{q > {q_{\rm{s}}}} \end{array}} \right., $ | (7) |
| $ \alpha=\left\{\begin{array}{ll} 1, & e_{\text {norm }}<0.525 \\ \frac{1}{\left(e_{\text {norm }}+0.457\right)^{0.575}}, & e_{\text {norm }}>0.525 \end{array}, \right. $ | (8) |
| $ {{e_{{\rm{norm}}}} = \frac{{{\rm{e}}{d_{\rm{p}}}}}{{2{k_{\rm{B}}}T}}E, } $ | (9) |
| $ {\tau = \frac{{4{\varepsilon _0}}}{{{\rho _{{\rm{ion}}}}{k_{{\rm{ion}}}}}}, } $ | (10) |
| $ {{q_{\rm{s}}} = 3\frac{{{\varepsilon _{\rm{r}}}}}{{{\varepsilon _{\rm{r}}} + 2}}{\rm{ \mathit{ π} }}{\varepsilon _0}d_{\rm{p}}^2E.} $ | (11) |
其中: qs是颗粒的饱和荷电量, ε0为真空介电常数, εr是烟气的相对介电常数, τ是颗粒荷电的时间常数(颗粒荷电量为饱和荷电量一半时所花费的时间), kB为玻尔兹曼常数而e为单位电子的电量。
1.4 颗粒受力模型本文采用拉格朗日方法对气相中悬浮粒子进行跟踪。在典型的静电除尘器质量加载速率下,气固两相流非常稀疏,颗粒间的相互作用可以忽略不计。Luo等[15]指出,流体拖曳力、Saffman升力和库仑力是经典ESP中颗粒所受的的主要体积力。而在本文的分析中,与流体阻力和库仑力相比,Saffman升力和重力被证明是微不足道的。此外,文献[7]指出纳米颗粒的布朗运动对于其扩散和沉积有着不可忽视的影响,因此,本文中纳米颗粒所受的体积力在这里主要考虑库仑力、曳力和布朗力,运动方程可以描述为
| $ \frac{{{\rm{d}}{\mathit{\boldsymbol{u}}_{\rm{p}}}}}{{{\rm{d}}t}} = \frac{{18\mu }}{{d_{\rm{p}}^2{\rho _{\rm{p}}}{C_{\rm{C}}}}}\left( {{\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{\rm{p}}}} \right) + \frac{{{q_{\rm{p}}}\mathit{\boldsymbol{E}}}}{{{m_{\rm{p}}}}} + {\zeta _i}\sqrt {\frac{{{\rm{ \mathit{ π} }}{S_0}}}{{\Delta t}}} , $ | (12) |
| $ {{C_{\rm{c}}} = 1 + \frac{{2\lambda }}{{{d_{\rm{p}}}}}\left( {1.257 + 0.4{{\rm{e}}^{ - 1.1{d_{\rm{p}}}/2\lambda }}} \right), } $ | (13) |
| $ {{S_0} = \frac{{216\upsilon {K_{\rm{B}}}T}}{{{{\rm{ \mathit{ π} }}^2}\rho d_{\rm{p}}^5{{\left( {{\rho _{\rm{p}}}/\rho } \right)}^2}{C_{\rm{C}}}}}.} $ | (14) |
式中:mp为颗粒质量, ug为烟气流速, up为颗粒运动速度, CC为康宁汉姆修正系数, λ是空气的平均自由程,Δt是颗粒的积分步长,ζi是高斯随机数。
2 物理模型及边界条件 2.1 几何模型建立为简化问题,在本文中采用的是二维的线板式ESP物理模型,其几何结构如图 1所示。集尘极的总长度为0.65 m,3根直径为5 mm的圆形电晕极以0.15 m的间距等距排列,电晕极与集尘极的距离为0.1 m。

|
Download:
|
| 图 1 ESP几何结构 Fig. 1 ESP geometric construction | |
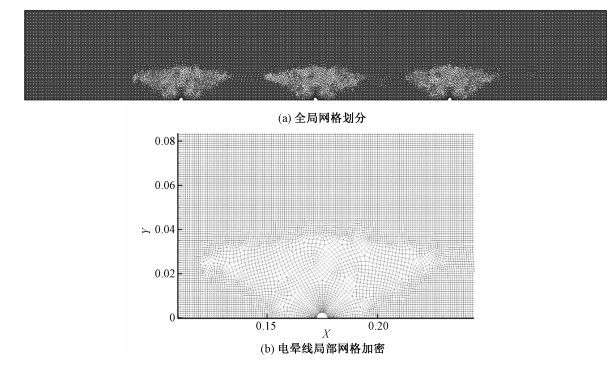
为降低计算量,以ESP水平中心线为轴对称选取模型的二分之一作为计算域并划分网格。在整个计算域中生成质量较高的结构化网格,并且由于电晕极周围电场强度梯度较大,对电晕极附近的网格进行加密。此外,考虑到计算结果对网格独立性的要求,对网格无关性进行了检验。采用33 098、62 879、91 645和209 811共4种不同网格数量计算同一工况(673 K, 进口流速0.3 m/s, 颗粒直径5 μm)下的颗粒收集效率,分别为31.9%、35.0%、35.1%和34.8%。考虑到当网格量大于62 879时颗粒收集效率已无显著变化,为提高计算效率,本文计算域划分网格数量取为62 879个,如图 2所示。
|
Download:
|
| 图 2 模型网格划分结构 Fig. 2 The grid scheme of the physical model | |
在数值计算中需要设定的边界条件,除流场和离散相模型外,数值模型中的电势和离子电荷密度2个标量也需要给定边界条件。电晕极表面的电势为运行电压,但电晕极表面的离子电荷密度则需要特别的处理,先用Peek定律计算得到电晕极的表面场强,随后迭代求解强耦合的离子电荷密度和表面场强,直到得到的表面场强值与Peek定律计算得到的场强值相等(一定残差范围内),取最终的离子电荷密度作为电晕极边界值。收尘板(接地极)处的电势为0,离子电荷密度通量为0。入口和出口的电势、离子电荷密度均为0。详细的边界条件如表 2所示。
|
|
表 2 边界条件 Table 2 Boundary conditions |
本文建立了ESP内纳米颗粒运动的数值模型,虽然该模型的电场、离子密度场和颗粒运动部分子模型已在之前经过验证[15],但由于本文所研究的对象为纳米尺寸的颗粒,荷电和受力特性都会发生变化,因此为了全面验证本文模型的可靠性,将模拟结果与Huang和Chen[10]所做的纳米颗粒在ESP中的穿透效率实验数据进行了对比。计算区域长300 mm, 板间距120 mm,线间距42 mm,放电极直径0.3 mm。模拟工况为: 烟气温度25 ℃,活性炭粒径为6~100 nm,烟气喷射量100 L/min。
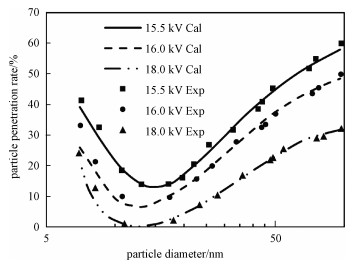
对3种不同运行电压下的纳米颗粒穿透率进行对比,如图 3所示。不难发现,无论在哪种运行电压下,本文模拟结果与实验结果在趋势上都吻合良好。纳米颗粒穿透效率呈现一个显著的U型转折,当颗粒粒径大于20 nm时,纳米颗粒穿透效率随着粒径的减小而减小,而当粒径小于20 nm时,纳米颗粒穿透效率随着粒径的减小而增大。这种穿透效率的变化趋势在微米和亚微米颗粒尺寸范围内并不会发生,说明纳米颗粒具有不同的运动和荷电特性,这种特点将在下文中深入讨论。但值得注意的是,在颗粒尺寸小于20 nm时,模拟得到的颗粒穿透效率在不同工况下都要略高于实验结果,最大偏差约为12.3%,这可能是由于纳米颗粒的部分荷电效应所引起的[16-17],即纳米颗粒尺寸在5~30 nm之间时,会出现颗粒荷电量急剧下降甚至不荷电的情况,而本模型所采用的荷电子模型并不能很准确地捕捉到这一效应,因此会略微高估这一区间内的颗粒荷电量,使得计算值中颗粒受到的电场力相对较大,从而高估了颗粒向电极板的迁移速度,使得模拟得到的除尘效率在这个区间内要略高于实验值。即使如此,本模型还是足以用来研究纳米颗粒在ESP内的运动荷电特性和20 nm以上的纳米颗粒的沉积效率。在未来的研究工作中将采用能更准确反应部分荷电效应对纳米颗粒沉积的影响的数值模型,这对于提高预测纳米颗粒沉积效率的准确度十分有帮助。
|
Download:
|
| 图 3 纳米颗粒除尘效率模拟结果与实验结果对比 Fig. 3 Comparison of nano particle removal efficiencies between modeling results and experimental data | |
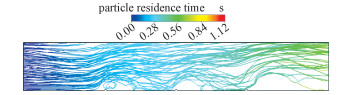
在典型的ESP运行工况下,即烟气温度120 ℃,烟气入口速度为1.0 m/s, 入口颗粒浓度为1 g/m3, 放电极运行电压为60 kV,向ESP的入口均匀喷射1 020个尺寸为100 nm的颗粒,图 4显示的是颗粒在ESP中的运动轨迹。由于电晕极的放电,颗粒在进入ESP后开始荷电,并在库仑力和曳力的共同作用下开始向收尘板方向偏转,可以看到部分颗粒在到达收尘板之前就已经逃逸出ESP。此外还有小部分粒子运动方向发生反转,这是由于ESP中的离子风形成漩涡将部分粒子卷携在低速的漩涡区中,增加了颗粒的停留时间。
|
Download:
|
| 图 4 纳米颗粒在ESP中的运动轨迹 Fig. 4 The trajectory of nano particle within the electrostatics precipitator | |
图 5展示颗粒在运动过程中所受曳力、库仑力和布朗力在X、Y两个坐标方向上的分量沿其运动轨迹的变化,其中X正向为主流方向,Y正向则是垂直极板向上的方向。可以看到,在100 nm这个尺寸,颗粒所受到的主要体积力和微米颗粒一样,仍然是曳力和电场力,其中曳力占主导地位,而布朗力的影响微乎其微。颗粒刚进入ESP内还未运动到第一根电极附近时,颗粒在离子风的作用下开始加速,在X轴方向气流将阻碍颗粒的运动,因此曳力在X轴的分力为负值,而电场力在X轴的分力为正值,使得颗粒在X轴方向的速度分量减小。在经过第1根电极线附近时,颗粒在X轴方向的速度已经小于气流的速度,因此曳力方向发生改变,由阻碍颗粒运动变为促进颗粒在X轴方向的运动,而电场力的X轴分量在第1根电极线之后几乎变为零,对于颗粒的运动没有影响。在颗粒经过第2根与第3根电极线时,颗粒在X轴方向再次经历2次加速,速度重新接近气相主流的速度,因此颗粒的X轴正向曳力也分别经历2次骤然减小的过程,直到减小为零,此后由于颗粒的速度又会超过气相,进入下一个循环过程,因此X轴方向曳力值会在零值线上下波动。而在Y轴方向上的电场力分力始终为正值,促使颗粒向极板方向迁移,在每次颗粒经过电极线时都会出现突跃。曳力在Y轴方向上的分力在第1根电极线之前为负值,当颗粒运动到电晕线附近时,Y方向上的电场力与曳力趋于平衡,颗粒的Y方向速度与气流Y方向速度相等,因此此时Y轴曳力分量为零,直到到达第2根电极线时才随着Y方向电场力的增加而重新变为负值,随后每次经过电极线时曳力都会减小,直到与电场力达到平衡,颗粒最终沉积在极板上。

|
Download:
|
| 图 5 纳米颗粒的沿程受力变化 Fig. 5 The body force on the nano particle along the flow | |
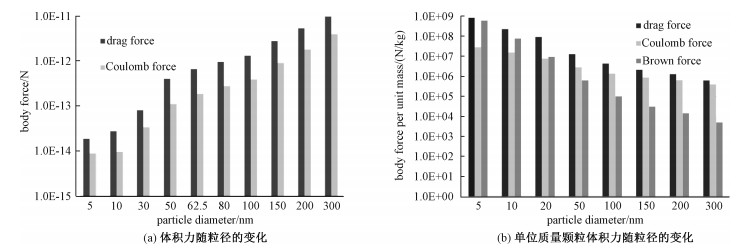
图 6(a)给出5~300 nm尺寸颗粒所受的曳力和库仑力的变化,显然随着颗粒粒径的减小,颗粒所受的总的静电力和曳力都在随着粒径的减小而减小,这与微米级颗粒的变化趋势一致[15]。曳力的减小是由于颗粒的惯性减小导致颗粒更容易被气流裹挟,从而气固相的相对速度减小,虽然曳力系数随着粒径的减小而增大,但相对速度对于曳力大小有着更为显著的影响。静电力随着粒径的减小而下降则主要是由于纳米颗粒的荷电量下降。在某些区间曳力减小的速率大于电场力减小的速率,从而使得颗粒驱进速度反而增加,这可能可以解释为什么纳米颗粒的沉积效率曲线会呈现U型,如图 3所示。而在微米级别的颗粒除尘效率都是随着颗粒粒径的减小而单调减小[15]。值得注意的是,当粒径小于20 nm时,颗粒沉积效率又开始随着粒径减小而减小。为解释这种现象,图 6(b)给出纳米颗粒单位质量的布朗力、曳力和库仑力的变化。可以看到单位质量电场力、曳力与布朗力均随着粒径的减小而增大。而且当粒径大于20 nm时,电场力与曳力占主导作用,但布朗力随着粒径的减小而增强,当粒径小于20 nm时,布朗力的大小已超过静电力,与曳力一同构成纳米颗粒所受的主要体积力。由于布朗力趋向于使颗粒进行无序的运动,因此不利于颗粒的沉积,因此在粒径小于20 nm时,纳米颗粒沉积效率又开始随着粒径下降而下降。
|
Download:
|
| 图 6 纳米颗粒的体积力随颗粒粒径的变化 Fig. 6 The body force on the nano particle for different particle diameters | |
此外,纳米颗粒的荷电特性也有着独特之处。颗粒荷电包括电场荷电和扩散荷电两种机制,电场荷电是气体离子在外加电场的作用下,做有序的运动,并与悬浮于气流中的粉尘颗粒碰撞所致,而扩散荷电则是由于离子做不规则运动时与气流中粉尘颗粒碰撞所致。微米与亚微米颗粒的主要荷电机制为电场荷电[6],扩散荷电量所占总荷电量比例很小。而由图 7(a)可以看到,当颗粒为100 nm以下的纳米颗粒时,电场荷电量要远小于扩散荷电量,且随着颗粒粒径的减小,电场荷电与扩散荷电的作用都会减小,当粒径小于20 nm时,颗粒的总荷电量趋近于零,说明本荷电模型能够在一定程度上反映较小尺寸纳米颗粒的部分荷电效应。而图 7(b)给出单位质量颗粒的扩散荷电量与电场荷电量的变化,呈现出与图 7(a)相反的趋势。单位质量的扩散荷电量仍远远大于电场荷电,但随着颗粒粒径的减小,扩散荷电量与电场荷电量呈现上升的趋势,这说明了图 6(b)中单位质量的电场力会随着粒径的减小而上升的原因。

|
Download:
|
| 图 7 纳米颗粒的荷电量随粒径的变化 Fig. 7 Charge for different particle sizes | |
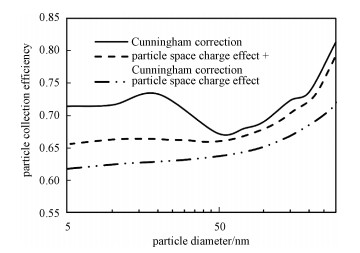
纳米颗粒之所以有独特的运动和荷电特性, 主要原因有2个: 一是当颗粒粒径到达纳米级时,颗粒的尺寸和空气自由程相接近,此时气体的连续性假设开始失效,因此曳力模型中加入了Cunningham修正系数来对纳米尺寸的颗粒所受曳力进行修正; 此外,上文提到粒径减小会使得单位质量颗粒的荷电量增加,这会对ESP内的电场和离子密度场造成不可忽视的影响,甚至造成电晕封闭的后果,因此不同于研究微米颗粒时通常忽略颗粒荷电对于电场的影响,在研究纳米颗粒应考虑颗粒荷电。图 8给出3种不同情况下(其他工况相同)纳米颗粒粒径对于颗粒沉积效率的影响,分别是只考虑Cunningham修正系数对曳力的影响、只考虑颗粒荷电对于电场的影响和同时考虑二者的影响。从图中可以看出,3种条件下的颗粒沉积效率有着明显的差异,只考虑Cunningham修正系数影响的情况沉积效率最大,而且与不考虑修正系数的情况相比较,效率的差距随着颗粒粒径的减小而加大,说明颗粒尺寸越小修正系数越大,对曳力的影响也就越大。而颗粒荷电效应的影响也十分明显,颗粒荷电显著地降低了颗粒的沉积效率,并且粒径越小此种下降就越明显。此外可以看到当只考虑颗粒荷电效应时沉积效率曲线并没有呈现出其他2种情况的U型曲线,而是随着粒径的减小单调下降,这说明考虑Cunningham修正系数所造成的曳力的减小是使得纳米颗粒在某些尺寸区间出现沉积效率上升的主要原因,只不过在同时考虑颗粒荷电对于电场的影响之后此种上升被抵消了一部分,效率曲线的U型转折相对来说不明显。
|
Download:
|
| 图 8 颗粒捕集效率随粒径的变化 Fig. 8 Particle collection efficiency for different particle sizes | |
上一节提到纳米颗粒荷电对于其沉积效率有着显著的影响,主要是通过影响ESP中的电场分布和电晕放电来体现的,本节研究纳米颗粒荷电对于ESP放电特性的作用机理。
图 9(a)给出电晕运行电压和放电电流密度的关系,其中对放电电流密度进行了无量纲化,方便评估颗粒荷电对于电晕放电抑制效果的强弱
| $ \text { current ratio }=\frac{J_{\text {corona }}}{J_{0}} \times 100 \% \text { , } $ | (15) |
其中: Jcorona是考虑颗粒荷电的电晕放电电流密度,J0则是不考虑颗粒荷电的电流密度。
从图 9(a)可以看到,纳米颗粒的荷电对于电晕的放电有着很明显的抑制效果,且随着运行电压的增加而削弱。这是由于当运行电压增加时,电场强度增加,抵消了部分纳米颗粒荷电量对于电场强度的负面影响,此外,电场力的增强使得颗粒向极板的驱进速度增加,减小电晕极附近的颗粒浓度,从而降低了颗粒电荷对于电晕发生的抑制效果。而这种电晕封闭作用也会随着颗粒尺寸的减小而增强,当颗粒尺寸从300 nm减小到30 nm时,60 kV电压下的相对电流密度减小77.3%,在较小电压下的电流密度几乎为零。这种抑制作用还体现在ESP的电压运行范围上,可以看到,随着粒径的减小,ESP的起晕电压增大,运行电压的范围被压缩。纳米颗粒的荷电对于电晕的这种较强的封闭作用,主要是由于小颗粒的比表面积较大,单位质量的颗粒荷电量较大,即式(3)中的ρpc较大,因此对于电场的分布有着不可忽略的影响。而且纳米颗粒的沉积率较低,悬浮在电晕线附近的颗粒较多,抑制了电晕的放电和离子的迁移。

|
Download:
|
| 图 9 不同工况下颗粒粒径对电晕放电电流的影响 Fig. 9 The influence of particle size on the current ratio under different operating conditions | |
图 9(b)显示在相同运行电压下,不同的颗粒入口浓度对于电晕放电密度的影响。显然随着颗粒浓度的增加,电晕封闭的作用就越强,当ESP中入口的纳米颗粒浓度达到一定值时,电晕放电被完全抑制,放电电流密度为零。这是由于颗粒浓度的增加直接增加了颗粒的荷电密度,抑制了离子的运动。值得注意的是,在颗粒浓度较小时,电晕电流密度随着颗粒浓度增加而减小的速率而在颗粒尺寸较小时更大,这也许是由于当颗粒浓度增加时降低的空间离子密度使得颗粒更难荷电,因此颗粒电荷密度的增加减缓,对电晕的抑制作用相对来说减弱了。此外,还可以看到,较大的颗粒不仅有着更高的电流密度,并且能够承受更大的颗粒入口浓度而不发生电晕封闭。
4 结论本文建立纳米颗粒ESP多场耦合数值模型,利用欧拉-拉格朗日方法研究纳米颗粒在ESP中的荷电和运动。研究表明在ESP中纳米颗粒具有与微米颗粒不同的沉积运动与荷电特性。
1) 模型预测的纳米颗粒沉积效率和实验得出的结果能够较好地吻合,可以准确地反映纳米颗粒的U型除尘效率曲线,但在颗粒粒径小于20 nm时模拟的除尘效率要略高于实验结果,这可能与纳米颗粒在20 nm以下会出现荷电不充分的现象有关,在将来的研究中将改进颗粒荷电模型以更准确的预测20 nm以下颗粒的沉积效率。
2) 纳米颗粒在ESP中的受力方向和受力大小会随着运动的进行而不断改变。颗粒尺寸为100 nm时,颗粒所受的主要体积力为库仑力和曳力。其中,库仑力在X轴的分量对于颗粒的影响较小,而库仑力的Y轴分量始终为正值,驱使颗粒向极板运动,并且在颗粒经过电极线时会升高。而曳力的X轴与Y轴分量的大小和方向则呈周期性变化,在经过电极线附近时由于电场力会使颗粒加速或减速,与气相的相对速度发生改变,因此曳力也会相应地改变方向和大小。
3) 纳米颗粒在ESP中有着独特的受力与荷电特性。当粒径大于20 nm时,曳力和库仑力构成颗粒主要的体积力,而当粒径小于20 nm时,布朗力的大小超过静电力,与曳力一同构成颗粒主要的体积力。纳米颗粒的荷电量主要来自于扩散荷电,且随着粒径的减小而减小,在5 nm时几乎为零,但单位质量的荷电量随着粒径的减小而增加。
4) 纳米颗粒所带的电荷和Cunningham系数对曳力的修正对于准确地预测纳米颗粒的沉积效率有着非常重要的影响,其中颗粒荷电将降低整体的沉积效率,而Cunningham系数是使沉积效率在尺寸50 nm左右开始上升的主要原因。
5) 纳米颗粒所带的电荷对于电晕放电有着较强的抑制作用,从而降低了荷电和沉积效率。小尺寸、高浓度的纳米颗粒会降低电晕放电电流密度,提高电晕起晕电压,压缩运行范围。颗粒的尺寸越小,浓度越大,对于电晕的封闭作用就越显著。
| [1] |
Weichenthal S, Dufresne A, Infante-Rivard C, et al. Indoor ultrafine particles and childhood asthma: exploring a potential public health concern[J]. Indoor Air, 2007, 17(2): 81-91. Doi:10.1111/j.1600-0668.2006.00446.x |
| [2] |
董雪玲. 大气可吸入颗粒物对环境和人体健康的危害[J]. 资源·产业, 2004, 6(5): 50-53. Doi:10.3969/j.issn.1673-2464.2004.05.014 |
| [3] |
陶燕, 刘亚梦, 米生权, 等. 大气细颗粒物的污染特征及对人体健康的影响[J]. 环境科学学报, 2014, 34(3): 592-597. |
| [4] |
Oberdörster G, Ferin J, Gelein R, et al. Role of the alveolar macrophage in lung injury: studies with ultrafine particles[J]. Environ Health Perspect, 1992, 97: 193-199. |
| [5] |
Donaldson K, Li X Y, Macnee W. Ultrafine (nanometre) particle mediated lung injury[J]. Journal of Aerosol Science, 1998, 29(5/6): 553-560. |
| [6] |
While H J. Industrial Electrostatic Precipitation[M]. New York: Addison-Wesley, 1963.
|
| [7] |
Saradari P T, Rahimzadeh H, Ahmadi G, et al. Nano-particle deposition in the presence of electric field[J]. Journal of Aerosol Science, 2018, 126: 169-179. Doi:10.1016/j.jaerosci.2018.09.012 |
| [8] |
Li A, Ahmadi G. Dispersion and deposition of spherical particles from point sources in a turbulent channel flow[J]. Aerosol Science and Technology, 1992, 16(4): 209-226. Doi:10.1080/02786829208959550 |
| [9] |
毕文剑, 李艳, 罗坤, 等. 温度对静电除尘器内颗粒受力影响的数值模拟[J]. 中国科学院大学学报, 2017, 34(2): 172-178. |
| [10] |
Huang S H, Chen C C. Ultrafine aerosol penetration through electrostatic precipitators[J]. Environmental Science & Technology, 2002, 36(21): 4625-4632. |
| [11] |
Lin G Y, Tsai C J. Numerical modeling of nanoparticle collection efficiency of single-stage wire-in-plate electrostatic precipitators[J]. Aerosol Science and Technology, 2010, 44(12): 1122-1130. Doi:10.1080/02786826.2010.512320 |
| [12] |
Lawless P A, Sparks L E. Modeling particulate charging in ESPs[J]. IEEE Transactions on Industry Applications, 1988, 24(5): 922-927. Doi:10.1109/28.8999 |
| [13] |
Li Y, Zheng C H, Luo K, et al. CFD simulation of high-temperature effect on EHD characteristics in a wire-plate electrostatic precipitator[J]. Chinese Journal of Chemical Engineering, 2015, 23(4): 633-640. Doi:10.1016/j.cjche.2014.06.038 |
| [14] |
Long Z W, Yao Q. Numerical simulation of the flow and the collection mechanism inside a scale hybrid particulate collector[J]. Powder Technology, 2012, 215/216: 26-27. Doi:10.1016/j.powtec.2011.08.045 |
| [15] |
Luo K, Li Y, Zheng C H, et al. Numerical simulation of temperature effect on particles behavior via electrostatic precipitators[J]. Applied Thermal Engineering, 2015, 88: 127-139. Doi:10.1016/j.applthermaleng.2014.11.078 |
| [16] |
Yoo K H, Lee J S, Oh M D. Charging and collection of submicron particles in two-stage parallel-plate electrostatic precipitators[J]. Aerosol Science and Technology, 1997, 27(3): 308-323. Doi:10.1080/02786829708965476 |
| [17] |
Zhuang Y, Kim Y J, Lee T G, et al. Experimental and theoretical studies of ultra-fine particle behavior in electrostatic precipitators[J]. Journal of Electrostatics, 2000, 48(3/4): 245-260. |
 2021, Vol. 38
2021, Vol. 38 


