近年来,数据采集和存储技术飞速发展,为数据分析提供了极大便利,但数据缺失的现象依旧频繁发生,严重影响数据分析的精度。特别是在小数据集背景下,缺失数据的存在将给数据分析工作带来灾难性的影响。因此,如何有效地对缺失数据进行填充成为亟待解决的关键问题。
目前,专家学者们在各个领域进行了大量的研究工作,提出了许多有效的缺失数据填充方法。插值方法[1-3]将已观测到的值拟合成平滑曲线,而后通过局部插值填充缺失值。该方法会随着时间的推移丢弃变量之间的关系,导致数据填充效果并不理想。另一类则是包括ARIMA(autoregressive integrated moving model)、SARIMA(seasonal ARIMA)[4-5]等在内的自回归方法,此类方法消除了时间序列数据中的非平稳部分,拟合出参数化的平稳模型来填充缺失数据。除此之外,文献[6]采用协同过滤的方法对推荐系统中的缺失值进行估计,文献[7]利用基于正则化的矩阵因子分解方法对定时采样的时间序列数据进行缺失值拟合,文献[8]结合迭代模型插值技术提出基于Aitchison距离的k近邻网络,文献[9]提出一种基于随机森林算法的迭代插值方法,文献[10]提出一种基于傅里叶变换和KNN(K-nearest neighbor)算法的时间序列缺失数据补全方法。然而,上述方法只能处理特定的缺失类型和应对较低缺失率的情况。
近年来,基于生成模型的方法在解决缺失数据填充问题上展现了优越的性能。文献[11]提出一种基于卷积自动编码器(convolutional autoencoder,CAE)的生理波数据缺失填充算法。该算法能在大量相邻的生理波数据段缺失的情况下进行填充,针对生理波形而言,该模型结构具有较强的一般性与扩展性;文献[12]提出一种去噪自编码器(denoising autoencoder,DAE)与生成对抗网络(generative adversarial network,GAN)相结合的模型,能够处理含噪声的高缺失率工业物联网数据。但是,该模型无法对高精度的数据进行填充;文献[13]提出DAE与堆叠自编码器(stacked autoencoder,SAE)结合的模型——堆叠去噪自编码器(denoising stacked autoencoder,DSAE),通过将缺失数据和观测数据看作一个整体恢复完整数据,可在不同缺失率情况下保持稳定的误差。但上述方法大都应用于大型数据集,应用到小数据集的效果不理想。
基于以上分析,本文提出一种基于改进神经过程(modified neural process,MNP)模型的缺失数据填充算法。该算法利用改进神经过程获得数据的分布函数模型,并通过训练来捕获对未观测点的不确定性,进而对数据缺失值进行估计。在训练阶段,根据缺失率引入采样率的修正系数,以提高高缺失率情况下的填充效果。仿真结果表明,缺失数据的填充值与真实值之间具有较低的平均相对误差;与其他算法相比,所提算法在高缺失率情况下的填充性能更优。
1 神经过程神经过程[14](neural process,NP)是一种结合了神经网络(neural network,NN)与高斯过程(Gaussian process,GP)两者优点的模型。基于深度神经网络强大的非线性拟合能力以及学习高斯过程的逼近方法,即学习在函数之上建模分布,能够根据上下文的观测估计其预测的不确定性。因此,NP又被称为是高斯过程的深度学习版本。
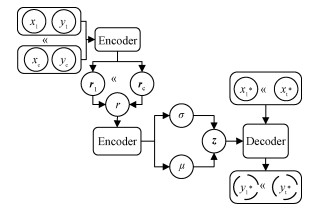
NP的模型结构如图 1所示。其中(xc, yc) 为上下文数据集,(x*t, yt*) 为目标数据集。通过模型结构图,可以将NP分解为以下几步:
|
Download:
|
| 图 1 NP模型结构图 Fig. 1 NP model structure diagram | |
1) 将上下文数据(xc,yc) 通过神经网络映射,获得其表征向量;
2) 将获得的表征向量进行聚合,得到单个表征值r;
3) 通过聚合后的表征值r对隐向量z进行参数化,使得隐向量z满足
| $ p\left( {\mathit{\boldsymbol{z}}\mid {x_{{\rm{1:c}}}},{y_{{\rm{1:c}}}}} \right) = N\left( {{\mu _\mathit{\boldsymbol{z}}}(r),\sigma _\mathit{\boldsymbol{z}}^2(r)} \right); $ | (1) |
4) 为了估计输入x*t后的函数值,对隐向量z进行采样,并与x*t一同输入到神经网络中,从而获得估计的x*t对应的函数值。
NP近似了两个分布,隐变量z的变分后验分布q(z|x1:n, y1:n) 和其条件先验分布p(z|x1:n, y1:n)[14],以KL散度推导出模型的训练损失函数,并称之为证据下界(ELBO),表示为
| $ \begin{array}{c} \mathrm{ELBO}=\mathbb{E}_{q\left(\mathit{\boldsymbol{z}} \mid x_{1: n}, y_{1: n}\right)}\left[\sum\nolimits_{j=1}^{n} \log p\left(y_{j} \mid \mathit{\boldsymbol{z}}, x_{j}\right)+\right. \\ \left.\log \frac{p(\mathit{\boldsymbol{z}})}{q\left(\mathit{\boldsymbol{z}} \mid x_{1: n}, y_{1: n}\right)}\right]. \end{array} $ | (2) |
设上下文集表示为(x1:m, y1:m),目标集表示为(xm+1:n, ym+1:n),又因为条件先验p(z|x1:m, y1:m) 在实验中难以求得,因此可用变分后验q(z|x1:m, y1:m) 近似代替,则有
| $ \begin{array}{c} \mathrm{ELBO}=\mathbb{E}_{q\left(\boldsymbol{z} \mid x_{1: n}, y_{1: n}\right)}\left[\sum\nolimits_{j=m+1}^{n} \log p\left(y_{j} \mid \boldsymbol{z}, x_{j}\right)+\right.\\ \left.\log \frac{q\left(\boldsymbol{z} \mid x_{1: m}, y_{1: m}\right)}{q\left(\boldsymbol{z} \mid x_{1: n}, y_{1: n}\right)}\right]. \end{array} $ | (3) |
GP是处理非平稳时间序列的常用方法,而NP是由GP和NN结合而成的,是GP的深度学习版本。NP通过NN确定核函数,具有很强的自适应性,可以很好地满足非平稳时间序列对核函数的要求。数据填充过程和时间序列的预测过程具有很高的相似度,可以先应用NP在已观测数据的基础上对整体数据的分布函数进行拟合,再利用获得的分布函数对缺失数据进行填充。但为使得在现有数据的基础上更好地反映完整数据的分布,需要对现有的NP进行修正。
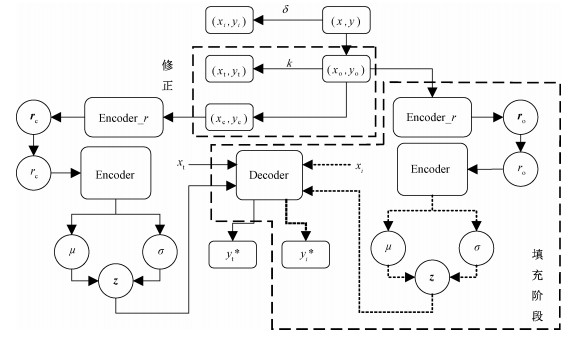
本文采用基于改进神经过程模型——MNP对缺失数据进行填充。模型结构图如图 2所示。其中,实线部分为训练过程,虚线部分为填充过程,填充过程中的Encoder_r、Encoder是经过训练过程学习得到的,与训练过程中的结构完全相同。图 2中变量含义如表 1所示。
|
Download:
|
| 图 2 MNP结构框图 Fig. 2 MNP model structure diagram | |
|
|
表 1 变量说明 Table 1 Variable declaration |
MNP算法在NP的基础上增加填充阶段,引入修正系数,使其在高缺失率的情况下能高效地对缺失数据进行填充。训练过程中,以k为采样比对观测数据进行随机采样,将其分为上下文集和目标集两部分。在计算模型的概率损失函数时,目标集也参与其中,这使得损失函数有意义,也有助于防止模型过拟合。并且在训练的过程中,反复以k为采样比对观测数据进行随机采样,使得上下文集对观测数据集有更为全面的概括,从而能更好地实现对观测数据集分布的描述;对上下文集进行学习,提取数据的特征,使得上下文集数据的分布近似观测数据的分布。填充阶段,将缺失数据近似作目标集,观测数据近似作上下文集。利用训练好的网络对观测数据进行特征提取,并根据提取的特征对缺失数据进行填充。具体算法过程如表 2所示。
|
|
表 2 MNP算法过程 Table 2 MNP algorithm process |
MNP模型继续沿用NP训练损失函数,在此处表示为
| $ \begin{aligned} \mathrm{ELBO}=& \mathbb{E}_{q(\boldsymbol{z} \mid \text { context }, \text { target })}\left[\sum\limits_{j=m+1}^{n} \log p\left(y_{j}^{*} \mid \boldsymbol{z}, x_{j}^{*}\right)+\right.\\ &\left.\log \frac{q(\boldsymbol{z} \mid \text { context })}{q(\boldsymbol{z} \mid \text { context }, \text { target })}\right]. \end{aligned} $ | (4) |
海洋表面温度(sea surface temperature,SST)是海洋的重要物理参数,在大气与海洋间的能量交换过程中扮演着重要的角色,是决定海气相互作用及气候变化的主要因素[15]。SST数据集[16]是由热带大气海洋项目的实测数据组成的,采样频率为1 h。从中选取1 000个连续采样的数据作为实验数据。SST数据现已广泛应用于多个领域,如赤潮研究、气候变化研究、海洋表面特征的解释以及各种勘察结果的解释。因此,监测海洋表面温度的变化,提供完整准确的海洋表面温度,对了解地区气候变化以及各种其他的海洋工作有重要意义。
北京PM2.5含量数据集是经由北京大学统计科学中心上传至UCI[17]数据库中,记录从2010年1月1日至2014年12月31日以1 h为采样频率记录的实时北京PM2.5含量值。
本文选择使用SST、北京PM2.5含量数据作为实验数据,以小数据集为背景,选取其中一个变量属性,分别从完整数据集中选取1 000个连续采样的数据作为时间序列,以此作为实验数据进行缺失数据填充的实验。
3.2 评价方法为了更好地反映缺失数据填充的效果,采用3种不同的方法对结果进行评价:均方误差(MSE)、平均相对误差(MRE)以及平均绝对误差(MAE),分别定义为:
| $ {\rm{MSE}} = \frac{{\sum\nolimits_N {{{\left( {y - {y^*}} \right)}^2}} }}{N}{\rm{,}} $ | (5) |
| $ {\rm{MRE}} = \frac{1}{N}\sum\nolimits_N {\frac{{y - {y^*}}}{y}} {\rm{,}} $ | (6) |
| $ {\rm{MAE}} = \frac{{\sum\nolimits_N {y - {y^*}} }}{N}, $ | (7) |
其中:N表示缺失值的数量,y为真实值,y*为模型估计的填充值。
4 实验结果本文选取SST数据和北京PM2.5含量数据作为实验数据,并对其进行预处理,然后对数据进行归一化,并将其按照缺失率为10%、20%、30%、40%、50%、60%、70%、80%、90%进行处理。
归一化过程具体表示为
| $ {x^\prime } = \frac{{x - {x_{{\rm{min}}}}}}{{{x_{{\rm{max}}}} - {x_{{\rm{min}}}}}}. $ | (8) |
本文实验分为3组,第1组实验为确定修正系数α的大小,进而确定修正后采样比k值的大小,即确定训练过程中所用数据集的大小;第2组为在确定修正后采样比k的情况下,各缺失率条件下的数据填充效果;第3组实验为本文模型与现有缺失数据填充模型的对比实验。
4.1 修正后采样比k值的确定定义k为
| $ k=\alpha \times \lambda, $ | (9) |
且k满足
| $ k=\frac{\text { len( target })}{\text { len( target }+\text { context })}, $ | (10) |
其中,λ为采样率,α为修正系数,且α满足α=f(δ),δ为缺失率。将训练集按照一定的采样率采样得到目标集(target),剩余数据作为上下文集(context)。
对α进行两种情况下的分析:
1) 针对不同的缺失率,k是固定不变的,即α=1;
2) k随缺失率的变化而变化,即α是δ的分段函数。
在训练过程中,通过NP模型对context集进行学习,利用target集的回归误差更新模型参数,进而获得整个训练集的数据分布函数。而填充阶段则根据训练阶段所学习的模型参数,估计需要的缺失值。在这两个过程中,存在两个比例:
| $ \begin{array}{l} 1)k = \frac{{{\rm{len}}\left( {{\rm{target}}} \right)}}{{{\rm{len}}\left( {{\rm{target + context}}} \right)}},\\ 2)\delta = \frac{{{\rm{len}}\left( {{\rm{缺失值}}} \right)}}{{{\rm{len}}\left( {{\rm{观测值 + 缺失值}}} \right)}}\;\;\;\;\;\;. \end{array} $ |
一方面,要求估计的缺失值与真实值之间的MRE最小,误差越小说明填充效果越好;另一方面,从模型本身出发,通过学习观测值的分布对缺失数据进行填充,要求训练过程中target数据的估计值误差与填充过程中缺失数据的估计值误差差值尽可能小,差值越小说明填充效果越好。
MSE与MAE描述的是估计值与真实值之间的绝对误差,而MRE描述两者之间的相对误差,不受数据归一化的影响。因此,为了更好地体现出所提算法的有效性,实验以MRE为主要评价标准对算法的填充效果进行评价。以SST数据和北京PM2.5含量数据为实验数据,对模型的性能进行检验,实验结果如图 3所示。

|
Download:
|
| 图 3 不同k不同缺失率情况下,训练与填充阶段估计数据的MRE误差情况 Fig. 3 MRE errors of data estimated during training and imputing under different k and missing rates | |
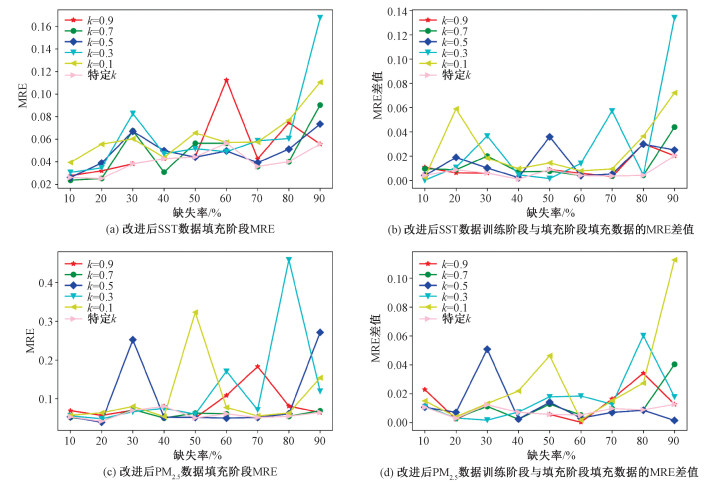
由实验结果可以看出,SST数据集与北京PM2.5含量数据集在不同缺失率情况下的实验效果较为一致,填充效果均随k值的变化而改变。随着缺失率的升高,整体的MRE呈现上升趋势,在个别k值处出现效果不好的点。
在图 3(a)、3(b)中,当k=0.1,在缺失率为20%、90%时训练阶段与填充阶段估计数据的误差过大;k=0.3,缺失率为30%、70%、90%时的差值同样过大,且在30%、90%时缺失数据的估计值MRE误差过大;k=0.9在缺失率为60%时缺失数据估计值的MRE过大。图 3(c)、3(d)中,当k=0.1时,算法在缺失率为50%处的填充误差较大,且在50%、80%、90%处的训练阶段与填充阶段估计数据的误差过大;当k=0.3时,算法在缺失率为60%、80%处的填充误差较大,且在80%处的差值同样存在较大的情况;当k=0.5时,在缺失率为30%、90%处的填充误差较大,且在30%处的训练阶段与填充阶段估计数据的误差过大。由此可以看出,在固定k不变时,算法不能保证多个缺失率情况下缺失数据的填充效果。当k随缺失率变化,即α是δ的分段函数时,算法的适应性更强。结合实验结果,可在每个缺失率处找到一个合适的k值。结果如表 3所示,选定k值后结果如图 4所示。
|
|
表 3 不同缺失率情况下k的取值情况 Table 3 k values at different miss rates |
|
Download:
|
| 图 4 不同缺失率情况下,固定k值与特定k值,训练与填充阶段估计数据的MRE误差情况 Fig. 4 MRE error of data estimated during training and imputing phase in the case of fixed k value and specific k value at different missing rates | |
通过实验1可确定在不同缺失率的情况下k的取值。由图 4可以看出,在两种不同数据集上得到的实验数据是一致的,因此在本实验中,仅在SST数据的基础上针对不同缺失率对缺失数据进行填充,实验效果如表 4所示。
|
|
表 4 不同缺失率情况下缺失值填充误差 Table 4 Imputing error of missing value with different missing rates |
由实验结果可以看出,所提算法能够在不同缺失率情况下实现缺失数据的填充。伴随着缺失率的升高,MAE与MSE的变化相对较为稳定,MRE随着缺失率的升高有所增大,但涨幅并不大,在可接受范围内。因此,该实验证明所提算法在不同缺失率情况下均能取得很好的效果。
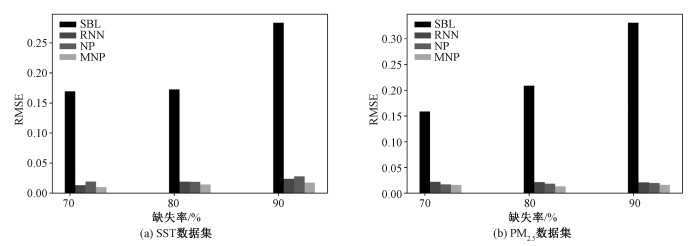
4.3 对比实验为验证所用模型的有效性,在两种不同的数据集上做了以下对比试验。所对比的方法有:1)稀疏贝叶斯算法[18](sparse bayesian learning,SBL);2)递归神经网络[19](recurrent neural network, RNN);3)神经过程(NP)。4种算法在不同缺失率情况下的RMSE对比如表 5所示,高缺失率情况下的RMES比较如图 5所示。
|
|
表 5 不同缺失率下4种填充算法的RMSE对比 Table 5 RMSE comparison of four imputing algorithms under different missing rates |
|
Download:
|
| 图 5 高缺失率条件下4种算法的RMSE比较 Fig. 5 RMSE comparison of four algorithms with high missing rates | |
由实验结果发现,在两种不同的小数据集上,4种算法均可实现缺失数据的填充,但是填充效果存在较大的差异。SBL算法可以处理缺失率较低的数据集,且精度要求不能过高;RNN算法在不同缺失率下的填充效果相较于SBL而言更优;基于NP模型的填充算法,其效果时而介于两者之间,时而优于RNN。不难发现,虽然SBL、RNN、NP 3种算法填充的缺失数据误差都随着缺失率的升高而增加,但MNP算法的填充误差能在不同缺失率的情况下保持相对稳定,且在每个缺失率下的误差均为最小;特别是在高缺失率的情况下,MNP的优势更加显著。同时,可以看出MNP的性能较NP算法有所提升,提高了填充精度,体现了修正系数的作用。并且,将4种算法应用于不同的数据集进行实验,由图 5可以看出,所提算法在高缺失率情况下,填充效果最优,NP与RNN效果相近,而SBL在高缺失率情况下的填充效果不佳;并且在高缺失率情况下,MNP在不同的实验数据集上具有相同的优异效果。
总体而言,基于MNP的填充算法能够在不同缺失率情况下有相对稳定的误差,且在高缺失率的情况下,MNP的性能优势更加显著。
5 总结本文提出一种基于改进神经过程的缺失数据填充算法,该算法将神经网络和高斯过程推理结合起来,弥补了两者的缺点,使其在小数据集背景下能够逼近多种不同的随机分布;该算法在NP的基础上增加填充过程,通过对观测数据的学习得到合适的分布,以此分布对缺失数据进行填充;算法通过引入修正系数α,提高了高缺失率情况下缺失数据的填充精度。该算法能在不同缺失率情况下有相对稳定的误差,且在高缺失率的情况下,MNP的性能优势更加显著。
由于修正系数为MNP模型的超参数,无法在训练阶段灵活地修改,使其缺少自适应性。并且,算法的应用背景是在单变量时间序列,缺乏多变量间的信息互反馈能力。因此,下一步的研究方向为使修正系数更具有自适应能力,增加模型的信息互反馈过程,从而解决多变量时间序列的缺失数据填充问题。
| [1] |
Kreindler D M, Lumsden C J. The effects of the irregular sample and missing data in time series analysis[J]. Nonlinear Dynamics Systems Analysis for the Behavioral Sciences Using Real Data. Boca Raton: CRC Press, 2016: 149-172.Psychology & Life Sciences, 2006, 10(2): 187-214.
|
| [2] |
Balouji E, Salor Ö, Ermis M. Exponential smoothing of multiple reference frame components with GPUs for real-time detection of time-varying harmonics and interharmonics of EAF currents[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6566-6575. Doi:10.1109/TIA.2018.2849059 |
| [3] |
Kozera R, Wilkołazka M. Natural spline interpolation and exponential parameterization for length estimation of curves[C]//AIP Conference Proceedings. Rhodes: AIP Publishing, 2017, 1863(1): 400010.
|
| [4] |
Newsham G R, Birt B J. Building-level occupancy data to improve ARIMA-based electricity use forecasts[C]//Proceedings of the 2nd ACM Workshop on Embedded Sensing Systems for Energy-Efficiency in Building. Zurich: ACM, 2010: 13-18.
|
| [5] |
Lippi M, Bertini M, Frasconi P. Short-term traffic flow forecasting: an experimental comparison of time-series analysis and supervised learning[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 871-882. Doi:10.1109/TITS.2013.2247040 |
| [6] |
Wang J, De Vries A P, Reinders M J T. Unifying user-based and item-based collaborative filtering approaches by similarity fusion[C]//Proceedings of the 29th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. Boston: ACM, 2006: 501-508.
|
| [7] |
Yu H F, Rao N, Dhillon I. Temporal regularized matrix factorization for high-dimensional time series prediction[C]//Advances in Neural Information Processing Systems. Barcelona: NIPS, 2016: 847-855.
|
| [8] |
Hron K, Templ M, Filzmoser P. Imputation of missing values for compositional data using classical and robust methods[J]. Computational Statistics & Data Analysis, 2010, 54(12): 3095-3107. |
| [9] |
Stekhoven D J, Bühlmann P. MissForest: non-parametric missing value imputation for mixed-type data[J]. Bioinformatics, 2012, 28(1): 112-118. Doi:10.1093/bioinformatics/btr597 |
| [10] |
Jia Z J, Song T W, Wang J X, et al. A time-series missing data completion method based on Fourier transform and kNNI algorithm[J]. Software Engineering, 2017, 20(3): 9-13. |
| [11] |
Miller D, Ward A, Bambos N, et al. Physiological waveform imputation of missing data using convolutional autoencoders[C]//2018 IEEE 20th International Conference on e-Health Networking, Applications and Services (Healthcom). Ostrawa: IEEE, 2018: 1-6.
|
| [12] |
Wang H, Yuan Z L, Chen Y B, et al. An industrial missing values processing method based on generating model[J]. Computer Networks, 2019, 158: 61-68. Doi:10.1016/j.comnet.2019.02.007 |
| [13] |
Duan Y J, Lü Y S, Kang W W, et al. A deep learning based approach for traffic data imputation[C]//17th International IEEE Conference on Intelligent Transportation Systems (ITSC). Qingdao: IEEE, 2014: 912-917.
|
| [14] |
Garnelo M, Schwarz J, Rosenbaum D, et al. Neural processes[J]. arXiv preprint arXiv: 1807.01622, 2018.
|
| [15] |
Wentz F J, Gentemann C, Smith D, et al. Satellite measurements of sea surface temperature through clouds[J]. Science, 2000, 288(5467): 847-850. Doi:10.1126/science.288.5467.847 |
| [16] |
NOAA/Pacific Marine Environmental Laboratory. Tropical atmosphere ocean[DB/OL].[2019-06-06]. http://www.pmel.noaa.gov/tao/proj_over/proj_over.html.
|
| [17] |
Dua D, Graff C. UCI Machine learning repository[DB/OL].[2019-07-30]. https://archive.ics.uci.edu/ml/datasets/ Beijing+PM2.5+Data.
|
| [18] |
Zhang Z L, Rao B D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 912-926. Doi:10.1109/JSTSP.2011.2159773 |
| [19] |
Strauman A S, Bianchi F M, Mikalsen K, et al. Classification of postoperative surgical site infections from blood measurements with missing data using recurrent neural networks[C]//2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI). Las Vegas: IEEE, 2018: 307-310.
|
 2021, Vol. 38
2021, Vol. 38 


