2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
复杂随机散射介质(如大气、生物组织和地形等)遮蔽目标的成像探测研究具有重要的现实意义。时间反转技术[1]由于其在复杂散射环境中表现出的成像潜力受到广泛的关注[2-4],从最初仅在声学领域应用,后来被扩展至电磁领域[5],如从水声通信、肾结石的检测与治疗、人体组织的超声聚焦至超带宽通信、穿墙成像、医疗成像等。时间反转技术的原理是波动方程的时间反转不变性,利用时间反转阵列(也称为时间反转镜)记录接收到的目标反射或散射信号,并将信号进行时间反转重发于探测区域从而实现对目标的成像[6]。在时间反转成像领域,时间反转镜成像仅能聚焦到散射最强的目标而失去了对弱散射目标的聚焦能力[7]。为克服时间反转镜成像法的缺点,基于空空多态数据矩阵(space-space multistatic data matrix,SS-MDM)的时间反转算子成像方法被提出。空空多数据矩阵的第i行第j列表示第j个天线单元发射探测信号到目标成像区域,第i个天线单元接收到的散射信号,由于每个矩阵元素与不同的空间位置有关,因此这种矩阵被称为空空多态数据矩阵。对时间反转算子进行特征值分解可以得到信号子空间和噪声子空间,空空时间反转算子分解法[8-9](decomposition of the time reversal operator,DORT)利用信号子空间进行成像。对于良好分辨目标,信号子空间是目标与时间反转阵列格林函数的共轭,利用空空DORT便可实现对目标的聚焦成像。但对于非良好分辨目标,信号子空间是目标与时间反转阵列格林函数共轭的线性组合,空空DORT不能在目标处实现聚焦成像。因此,利用噪声子空间进行成像的空空时间反转多信号分类(time reversal multiple signal classification, TR-MUSIC)成像[10-11]被提出。噪声子空间始终与信号子空间正交,因此即使不满足良好分辨准则,利用噪声子空间成像的空空TR-MUSIC也能实现对目标的良好聚焦。相较于空空DORT,空空TR-MUSIC具有更好的成像分辨率。虽然空空TR-MUSIC的分辨率有所提高,但其抗噪性和成像稳定性较差[12-13],易受杂波的影响导致分辨变差或者失去对目标的聚焦能力。此外,空空多态数据矩阵的获取较为复杂,时间反转阵列的每个天线依次发射信号,所有天线需要分别接收目标的散射信号并储存,因此不能实现对目标的实时性聚焦。针对空空DORT和TR-MUSIC对随机介质背景下目标的探测,学者已经展开研究,并对影响成像结果的因素进行分析[14-16]。空频多态数据矩阵(space-frequency multistatic data matrix,SF-MDM)是为了确定生物医学中病变的三维位置和电参数,在传统的MUSIC算法背景下提出的[17],其是一个天线发射信号,所有天线接收目标回波信号。该矩阵的行和列分别对应于接收信号的空间位置和频率信息,因此被称为空频多态数据矩阵。基于空频多态数据矩阵的DORT成像算法即空频DORT目前已被提出[18-19],虽然该方法相较于空空DORT具有较强的抗噪性能,但其分辨率仍较差,不能实现对复杂散射环境中目标的准确成像[20]。
为克服传统空空TR-MUSIC的缺点,以实现对复杂散射环境中目标的准确成像,本文提出空频TR-MUSIC,利用空频多态数据矩阵,将发射信号和噪声子空间结合得到需要回传的时间反转信号,与探测区域的搜索点格林函数相乘,实现对目标的聚焦成像。
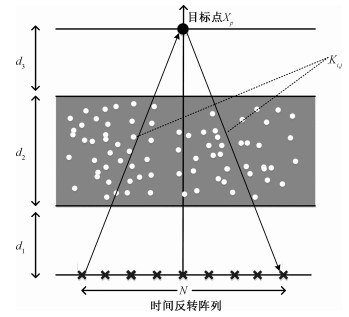
1 空频TR-MUSIC成像理论分析成像场景如图 1所示,在探测区域的底部放置N个收发同置的天线,Ri(i=1, …, N)为时间反转阵列第i个天线的位置,Xp为探测区域内目标的位置。假设目标为理想点目标,天线为理想点天线。随机介质位于天线阵列与目标之间其厚度为d2,天线距随机介质下表层间距为d1,目标距随机介质上表层间距为d3。K为多态数据矩阵,其中每个元素Ki, j(i, j=1, …, N)表示第j个天线发射信号到探测区域,第i个天线接收到的散射场信号。天线发射的高斯脉冲信号为
| $ f(t) = {\rm{exp}} \left( { - \frac{{{t^2}}}{{{T^2}}} - {\rm{i}}{w_{\rm{c}}}t} \right), $ | (1) |
|
Download:
|
| 图 1 成像场景 Fig. 1 Imaging scene | |
其中:T为信号的脉冲宽度,wc为信号的载频。
1.1 自由空间中目标成像理论分析本文先考虑自由空间中目标的成像,即图 1中的随机介质不存在的情况。假设第n个天线发射短脉冲,时间反转阵列的所有N个天线接收回波散射信号,对回波信号做M点采样产生N×M阶的SF-MDM Kn(w) 为:
| $ \boldsymbol{K}_{n}(\omega)=\left[\begin{array}{cccc} k_{1 n}\left(w_{1}\right) & k_{1 n}\left(w_{2}\right) & \cdots & k_{1 n}\left(w_{M}\right) \\ k_{2 n}\left(w_{1}\right) & k_{2 n}\left(w_{2}\right) & \cdots & k_{2 n}\left(w_{M}\right) \\ \cdots & \cdots & \cdots & \cdots \\ k_{N n}\left(w_{1}\right) & k_{N n}\left(w_{2}\right) & \cdots & k_{N n}\left(w_{M}\right) \end{array}\right], $ | (2) |
其中:矩阵中的第n行表示第n个天线采集的时域信号进行傅里叶变换后的频域采样值,wM-w1为信号的带宽。对Kn(w) 进行奇异值分解可得
| $ \boldsymbol{K}_{n}(w)=\boldsymbol{U}_{n}(w) \boldsymbol{\varLambda}_{n}(w) \boldsymbol{V}_{n}{ }^{\mathrm{H}}(w), $ | (3) |
其中:Un是表示左奇异矢量的N×N阶矩阵,Vn是表示右奇异矢量的M×M阶矩阵,Λn是N×M阶的奇异值矩阵,上标H表示伴随算符,若A=(ai, j)则AH=(aji*)。当有Ms个目标时,Λn有Ms个非零奇异值,其对应的奇异向量{usub1(w), …, usubMs(w)}形成信号子空间,剩下的N-Ms个奇异值对应的奇异向量{usubMs+1(w), …, usubN(w)}构成噪声子空间。第p(p=1, …, Ms)个目标对应的信号子空间奇异向量upsubn的幅度和相位表示天线与目标的位置关系,决定时间反转信号的幅度和相位。结合发射信号S(t)的频谱信息S(w),利用噪声子空间可得需要回传的时间反转信号为
| $ \sum\limits_{i=M_{s}+1}^{N} s_{\mathrm{TR}-n}^{i}=\sum\limits_{i=M_{s}(w)+1}^{N} \boldsymbol{u}_{\mathrm{sub}_{n}}^{i} S(w). $ | (4) |
在确定需要回传的时间反转信号之后,目标的成像函数需要利用探测区域每个搜索点Xs处的背景格林函数矢量(导向矢量) g(Xs, w),如下式:
| $ \mathit{\boldsymbol{g}}({\mathit{\boldsymbol{X}}_s},w) = {[G({\mathit{\boldsymbol{X}}_s},{\mathit{\boldsymbol{R}}_1},w), \cdots ,G({\mathit{\boldsymbol{X}}_s},{\mathit{\boldsymbol{R}}_N},w)]^{\rm{T}}}. $ | (5) |
其中,G(Xs, Ri, w) 是背景格林函数。本文用自由空间导向矢量g0(Xs, w)=[G0(Xs, R1, w), …, G0(Xs, RN, w)]T近似g(Xs, w)。由此可知空频TR-MUSIC成像函数为
| $ \begin{array}{c} M_{\mathrm{SF}}\left(\boldsymbol{X}_{s}, w\right)=\left(\sum\limits_{i=M_{s}(w)+1}^{N}\left|\left\langle s_{\mathrm{TR}-n}^{i}(w), \boldsymbol{g}\left(\boldsymbol{X}_{s}, w\right)\right\rangle\right|^{2}\right)^{-1} =\\ \left(\sum\limits_{i=M_{s}+1}^{N}\left|\int_{\Omega} S^{\mathrm{H}}(w)\left[\boldsymbol{u}_{\mathrm{sub}_{n}}^{i}\right]^{\mathrm{H}} \boldsymbol{g}\left(\boldsymbol{X}_{s}, w\right) \mathrm{d} w\right|^{2}\right)^{-1}. \end{array} $ | (6) |
由于分解后的左奇异矢量ui, i=1, …, N形成包含传感器位置信息的正交集,右奇异矢量vi, i=1, …, N形成包含频率信息的正交集。因此,Kn(ω)为空频多态数据矩阵,将Kn(ω)的分解称为空频分解,将基于空频分解的成像方法称为空频成像。
以上讨论的是第n天线发射信号,所有天线接收散射场数据的情况。若天线阵列的每个天线依次发射信号,所有天线接收并保存散射场数据。当n=1, …, N,对所有Kn(ω)进行组合可得基于完备数据的空频多态矩阵K(ω) (full data based SF-MDM,FD-SF-MDM)为
| $ \boldsymbol{K}(w)=\left[\begin{array}{cccc} \boldsymbol{k}_{1 n}\left(w_{1}\right) & \boldsymbol{k}_{1 n}\left(w_{2}\right) & \cdots & \boldsymbol{k}_{1 n}\left(w_{M}\right) \\ \boldsymbol{k}_{2 n}\left(w_{1}\right) & \boldsymbol{k}_{2 n}\left(w_{2}\right) & \cdots & \boldsymbol{k}_{2 n}\left(w_{M}\right) \\ \cdots & \cdots & \cdots & \cdots \\ \boldsymbol{k}_{N n}\left(w_{1}\right) & \boldsymbol{k}_{N n}\left(w_{2}\right) & \cdots & \boldsymbol{k}_{N n}\left(w_{M}\right) \end{array}\right], $ | (7) |
| $ \begin{array}{c} \boldsymbol{k}_{i, n}\left(w_{1}\right)=\left[k_{i, 1}\left(w_{1}\right), k_{i, 2}\left(w_{1}\right), \cdots, k_{i, N}\left(w_{1}\right)\right], \\ (i, n=1, \cdots, N). \end{array} $ |
对K(ω)进行奇异值分解可得
| $ \mathit{\boldsymbol{K}}(w) = \mathit{\boldsymbol{U}}(w)\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}(w){\mathit{\boldsymbol{V}}^{\rm{H}}}(w), $ | (8) |
其中:U是N2×N2阶的左奇异向量矩阵,Λ是N2×M阶的奇异值矩阵,V是M×M阶的右奇异矢量矩阵。矩阵U与目标对应的列向量构成信号子空间,剩余的列向量构成噪声子空间。信号子空间每列包含N个子向量Usubn, n=1, …, N,每个子向量Usubn包含N个元素,每个元素之间的相位差包含目标空域信息。用Up表示与第p个目标相对应的第p列向量。用Upsubn表示与第p个目标相对应的第n个子向量,n=1, …, N,p=1, …, Ms。噪声子空间包含N个矩阵Usubn(n=1, …, N),每个子矩阵Uisubn包含N-Ms+1个列向量{uMs+1subn(w), …, uNsubn(w)},每个列向量包含N个元素。结合发射信号频谱信息S(w),利用噪声子空间可得需要回传的时间反转信号为
| $ \sum\limits_{n=1}^{N} \sum\limits_{i=M_{s}+1}^{N} s_{\mathrm{TR}-n}^{i}(w)=\sum\limits_{n=1}^{N} \sum\limits_{i=M_{s}+1}^{N} \boldsymbol{u}_{\mathrm{sub}_{n}}^{i}(w) S(w). $ | (9) |
因此,基于完备数据的空频TR-MUSIC成像函数为
| $ \begin{array}{l} M_{\mathrm{SF}}^{\mathrm{full}}\left(\boldsymbol{X}_{s}, w\right)=\left(\sum\limits_{n=1}^{N} \sum\limits_{i=M_{s}+1}^{N}\left|\left\langle s_{\mathrm{TR}-n}^{i}(w) \boldsymbol{g}\left(\boldsymbol{X}_{s}, w\right)\right\rangle\right|^{2}\right)^{-1}= \\ \left(\sum\limits_{n=1}^{N} \sum\limits_{i=M_{s}+1}^{N}\left|\int_{\Omega} S^{\mathrm{H}}(w)\left(\boldsymbol{u}_{\mathrm{sub}_{n}}^{i}\right)^{\mathrm{H}} \boldsymbol{g}\left(\boldsymbol{X}_{s}, w\right) \mathrm{d} w\right|^{2}\right)^{-1}. \end{array} $ | (10) |
对于单频空空TR-MUSIC成像,SS-MDM的获取较为复杂,时间反转阵列的N个天线依次发射信号,所有天线需要分别接收目标的回波信号并储存,因此不能实现对目标的实时性聚焦。空频TR-MUSIC式(6)可以克服这一缺点,SF-MDM是一个天线发射信号,所有天线接收回波信号,使成像的实时性得到了满足。由于基于完备数据的空频TR-MUSIC成像式(10)考虑了N个子噪声矩阵的共同作用,即相当于N次叠加取平均,具有统计特性,对噪声干扰具有一定的抑制作用。而多频空空TR-MUSIC成像考虑有效带宽内的所有频点对目标成像的贡献,具有数值稳定性。鉴于数据的完备性和成像的稳定性,若无特别指出,下文中对于自由空间中和随机介质背景下目标的成像均采用多频空空TR-MUSIC与基于完备数据的空频TR-MUSIC。
1.2 随机介质背景下目标成像理论分析上述是对自由空间中目标的成像分析,当目标和天线之间存在随机介质时,还需要考虑随机介质对目标成像的影响。根据辐射传输方程理论,电磁波在随机介质中的衰减可以用光学厚度(optical depth,OD)来描述[21],光学厚度等于光学散射厚度加上光学吸收厚度。若τo表示光学厚度,τs表示光学散射厚度,τa表示光学吸收厚度,则其表达式分别为:
| $ \tau_{\mathrm{o}}=\int \rho \sigma_{\mathrm{e}} \mathrm{d} s , $ | (11a) |
| $ \tau_{\mathrm{s}}=\int \rho \sigma_{\mathrm{s}} \mathrm{d} s, $ | (11b) |
| $ {\tau _{\rm{a}}} = \int \rho {\sigma _{\rm{a}}}{\rm{d}}s. $ | (11c) |
其中:ρ表示粒子数密度,σe表示单个粒子的消光截面,σa表示单个粒子的吸收截面,σs表示单个粒子的散射截面。对于特定的介质,散射厚度与光学厚度的比值即单次散射反照率(Albedo)为定值。
对于随机介质背景下目标的成像仅考虑单目标的情况,假设该目标是具有恒定散射幅度的各向同性散射体。阵列天线、目标与搜索点位于同一平面内,成像场景如图 1所示。N个天线阵列,第j个天线发射高斯脉冲信号,电磁波穿过随机介质入射到目标上,目标对入射波发生散射,其散射系数为τ,散射波穿过随机介质被第i个天线接收,则第j个天线和第i个天线之间的传输函数可用随机格林函数表示为
| $ K_{i j}=\tau G\left(\boldsymbol{R}_{j}, \boldsymbol{X}_{p}\right) G\left(\boldsymbol{X}_{p}, \boldsymbol{R}_{i}\right). $ | (12) |
N个天线发射,N个天线接收,则可得到传输矩阵为
| $ \boldsymbol{K}=\tau \boldsymbol{gg} ^{\mathrm{T}} , $ | (13) |
其中:g=[G(R1, Xp, w), G(R2, Xp, w), …, G(RN, Xp, w)]T,τ设为1,由此可得
| $ \boldsymbol{T}=\boldsymbol{K} \boldsymbol{K}^{\mathrm{H}}=\boldsymbol{g} \boldsymbol{g}^{\mathrm{T}} \boldsymbol{g}^{*} \boldsymbol{g}^{\prime}. $ | (14) |
当随机介质存在时,T矩阵用集平均的形式表示为
| $ \langle\boldsymbol{T}\rangle=\left\langle\boldsymbol{K} \boldsymbol{K}^{\mathrm{H}}\right\rangle=\left\langle\boldsymbol{g} \boldsymbol{g}^{\mathrm{T}} \boldsymbol{g}^{*} \boldsymbol{g}^{\prime}\right\rangle, $ | (15) |
则矩阵T的每一项为
| $ \left\langle T_{m n}\right\rangle=\sum\limits_{i=1}^{N}\left\langle G_{m}^{*} G_{n} G_{i} G_{i}^{*}\right\rangle. $ | (16) |
对于波在随机介质中传播的大扰动和小扰动,圆复高斯近似假设均可以给出正确的限制条件。利用圆复高斯近似假设可将四阶矩〈Gm*GnGiGi*〉由二阶矩[22]表示为
| $ \begin{aligned} \left\langle G_{m}^{*} G_{n} G_{i} G_{i}^{*}\right\rangle &=\left\langle G_{m}^{*} G_{n}\right\rangle\left\langle G_{i} G_{i}^{*}\right\rangle+\left\langle G_{m}^{*} G_{i}\right\rangle\left\langle G_{n} G_{i}^{*}\right\rangle-\\ &\left\langle G_{m}^{*}\right\rangle\left\langle G_{n}\right\rangle\left\langle G_{i}\right\rangle\left\langle G_{i}^{*}\right\rangle, \end{aligned} $ | (17) |
由双频互相干函数可将二阶矩表示为
| $ \left\langle G_{i} G_{j}^{*}\right\rangle=\Gamma_{i, j}\left(w_{1}, w_{2}\right), $ | (18) |
利用抛物线近似可得
| $ \Gamma_{i, j}=G_{i o}\left(w_{1}\right) G_{j o}\left(w_{2}\right) \exp \left(-Q_{i, j}\right), $ | (19) |
Gio为自由空间中的格林函数,其表达式为
| $ G_{i o}=-\frac{i}{4} H_{0}^{(1)}\left(k_{1}\left|\boldsymbol{R}_{i}-\boldsymbol{X}_{p}\right|\right), k_{1}=\frac{w_{1}}{c}, $ | (20) |
式中,H0(1)为第一类零阶汉克尔函数。
随机介质的散射特性由单个散射体散射模式的相函数ρ(s) 获得。在解析模型中,假设ρ(s) 为高斯相函数
| $ p(s)=4 \alpha_{p} \exp \left(-\alpha_{p} s^{2}\right), $ | (21) |
其中:s=2sin(θ/2),θ是散射角。αp是相位函数的角度分布,其表达式为
| $ \alpha_{p}=\frac{\bar{\mu} \ln 2}{(1-\bar{\mu})^{2}\left(2^{2 / 3}-1\right)}, $ | (22) |
其中:μ是各向异性因子,是散射角的平均余弦。典型的各向异性因子值为0.85,αp则为44.58。因此本文中的随机介质均是指均匀随机介质。
因子exp(-Qi, j)表示随机介质的影响,为相干分量与非相干分量的总和[23]。相干强度与exp(-τo)成正比,非相干强度与exp(-Qij)-exp(-τo)成正比,ρo是指当非相干强度减小到峰值的exp(-1)的距离。利用式(21)与式(22)将exp(-Qi, j) 近似表示为:
| $ \exp \left(-Q_{i, j}\right)=\exp \left(-\tau_{o}\right)+F_{s} X_{i j}, $ | (23) |
| $ F_{s}=1-\exp \left(-\tau_{s}\right) , $ | (24a) |
| $ X_{i j}=\exp \left(-\tau_{a}-\frac{\left|r_{i}-r_{j}\right|^{2}}{\rho_{o}^{2}}\right), $ | (24b) |
| $ \frac{1}{\rho_{o}^{2}}=\frac{\tau_{s} k^{2}\left[\left(d_{1}+d_{2}\right)^{3}-d_{1}^{3}\right]}{12 \alpha_{p} L^{2} d_{2} F_{s}}. $ | (24c) |
由式(17)、式(19)与式(23)可得二阶矩与四阶矩分别为:
| $ \left\langle G_{i} G_{j}^{*}\right\rangle=G_{i o}\left(w_{1}\right) G_{j o}\left(w_{2}\right)\left(\exp \left(-\tau_{o}\right)+F_{s} X_{i j}\right), $ | (25) |
| $ \begin{array}{c} \left\langle G_{m}^{*} G_{n} G_{i} G_{i}^{*}\right\rangle=\left[G_{m o}^{*} G_{i o}^{*} G_{n o} G_{i o}\right]\left\{\exp \left(-2 \tau_{o}\right)+\right. \\ F_{s} \exp \left(-\tau_{o}\right)\left(X_{i i}+X_{n m}+X_{i m}+X_{n i}\right)+ \\ \left.F_{s}^{2}\left(X_{n m} X_{i i}+X_{i m} X_{n i}\right)\right\}. \end{array} $ | (26) |
将式(25)代入式(15)中可求得时间反转矩阵〈T〉的解析解表达式,关于对随机介质的更多描述详见文献[3, 14]。
对于空频TR-MUSIC成像,K矩阵的每列为
| $ \begin{array}{c} \boldsymbol{K}\left(w_{m}\right)=\left[\begin{array}{l} \boldsymbol{k}_{1 n}\left(w_{m}\right) \\ \boldsymbol{k}_{2 n}\left(w_{m}\right) \\ \cdots \\ \boldsymbol{k}_{N n}\left(w_{m}\right) \end{array}\right]= \\ {\left[\begin{array}{cccc} k_{11}\left(w_{m}\right) & k_{12}\left(w_{m}\right) & \cdots & k_{1 N}\left(w_{m}\right) \\ k_{21}\left(w_{m}\right) & k_{22}\left(w_{m}\right) & \cdots & k_{2 N}\left(w_{m}\right) \\ \cdots & \cdots & \cdots & \cdots \\ k_{N 1}\left(w_{m}\right) & k_{N 2}\left(w_{m}\right) & \cdots & k_{N N}\left(w_{m}\right) \end{array}\right],} \end{array} $ | (27) |
其中,m=1, …, M。由T(ωm)=K(wm)K(wm)H可得
| $ \boldsymbol{T}(w)=\left[\begin{array}{cccc} \boldsymbol{t}_{1 n}\left(w_{1}\right) & \boldsymbol{t}_{1 n}\left(w_{2}\right) & \cdots & \boldsymbol{t}_{1 n}\left(w_{M}\right) \\ \boldsymbol{t}_{2 n}\left(w_{1}\right) & \boldsymbol{t}_{2 n}\left(w_{2}\right) & \cdots & \boldsymbol{t}_{2 n}\left(w_{M}\right) \\ \cdots & \cdots & \cdots & \cdots \\ \boldsymbol{t}_{N n}\left(w_{1}\right) & \boldsymbol{t}_{N n}\left(w_{2}\right) & \cdots & \boldsymbol{t}_{N n}\left(w_{M}\right) \end{array}\right]. $ | (28) |
由Gmo*Gio*GnoGio=kmiH(w)kni(w),考虑随机介质对T矩阵的影响,对T矩阵进行奇异值分解,利用噪声子空间进行成像。
2 成像结果分析成像的参数设置如表 1所示,天线间隔为λc/2以减少相互耦合,成像区域网格大小为λc/4×λc/4。首先考虑自由空间中的成像,随后对随机介质背景下目标的成像效果进行分析。
|
|
表 1 成像参数设置 Table 1 Imaging parameter setting |
空空TRMUSIC和空频TRMUSIC均可实现对自由空间中目标的成像。由图 2可知,对于单目标成像,二者均具有较好的定位效果,但空频TR-MUSIC具有较小的成像点。这是因为空频TR-MUSIC成像是对FD-SF-MDM进行奇异值分解,得到的左奇异向量矩阵仅包含天线阵列与目标的空间关系,将噪声子空间与发射信号结合,回波信号包含的目标信息为阵元的初始发射信号分配不同的幅值和相位,使阵元在不同的延时后发射信号,从而实现对目标的聚焦成像。而空空TR-MUSIC则是利用由多个频点处SS-MDM特征值分解得到的特征向量作为回传信号。中心频点处的噪声子空间与背景格林函数存在很强的正交关系,但随着频率与中心频点的偏移,导致这种正交性减弱,因此造成了成像点的增大。

|
Download:
|
| (a, b)二维与三维空空TR-MUSIC成像结果, (c, d)二维与三维空频TR-MUSIC成像结果。 图 2 自由空间中成像 Fig. 2 Imaging in free space (2D and 3D imaging result of the space-space TR-MUSIC (a, b) and 2D and 3D imaging result of the space-frequency TR-MUSIC (c, d)) | |
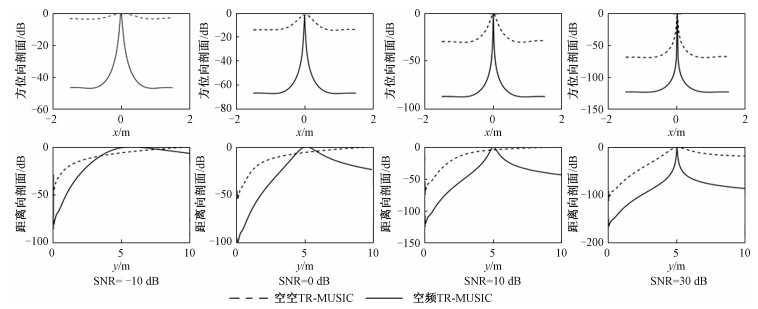
为分析空空TR-MUSIC和空频TR-MUSIC的抗噪性,在获取目标的散射场数据后,为每一采样点叠加不同信噪比的高斯白噪声。从图 3中可以看出空频TR-MUSIC的抗噪性能明显优于空空TR-MUSIC。当叠加信噪比为-10 dB的高斯白噪声时,空频TR-MUSIC虽然出现位置的偏移但仍能实现对目标的成像,而空空TR-MUSIC则散焦严重,完全不能实现对目标的成像;当叠加信噪比为0 dB的高斯白噪声时,空空TR-MUSIC不能实现对目标的成像,空频TR-MUSIC成像点明显减小;当叠加信噪比为10 dB的高斯白噪声时,空空TR-MUSIC的散焦有所改善,但仍不能实现对目标的聚焦,而空频TR-MUSIC受噪声的影响较小,能实现对目标的准确成像;当叠加信噪比为30 dB的高斯白噪声时,两种成像方法均能实现对目标的准确成像,相较于空空TR-MUSIC,空频TR-MUSIC具有较小的成像点。图 4给出目标T1在不同信噪比的高斯白噪声下方位向和距离向的成像分辨率,由图可知两种成像方法均是方位向分辨率优于距离向分辨率,方位向峰值能准确地与目标方位向坐标位置重合,但距离向峰值会有所偏离,叠加的噪声越强,距离向峰值与目标真实距离向位置偏移越大。

|
Download:
|
| 上: 空空TR-MUSIC; 下: 空频TR-MUSIC。 图 3 不同噪声条件下成像结果比较 Fig. 3 Imaging results comparison under different noises (the first row is space-space TR-MUSIC, the second row is space-frequency TR-MUSIC) | |
|
Download:
|
| 图 4 不同噪声条件下成像分辨率比较 Fig. 4 Imaging resolution comparison under different noise | |
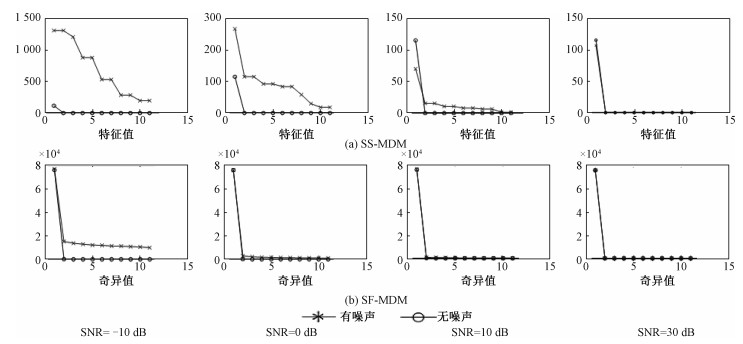
在自由空间中,一个目标仅存在一个大于0的特征值或奇异值。当存在噪声时,一个目标会出现若干个大于0的特征值或奇异值,从而导致成像效果的恶化。从图 5可以看出,在相同噪声情况下,SS-MDM的特征值受噪声的影响较大。SF-MDM的奇异值仅在信噪比为-10 dB时受到的影响较大,不能实现对目标的聚焦,当信噪比为0和10 dB时,奇异值受到的影响较小,成像效果较好。
|
Download:
|
| 图 5 不同噪声下中心频点处SS-MDM的特征值和SF-MDM奇异值 Fig. 5 The eigenvalue of SS-MDM at the center frequency and the singular value of SF-MDM under different noises | |
根据1.2节给出的理论模型,利用空空TR-MUSIC进行成像,图 6给出不同随机介质背景下目标成像结果图。当OD=0.1,Albedo=0.1时,空空TR-MUSIC能实现对目标的准确成像;随着单次散射反照率的增加,虽然成像结果在纵向上出现了散焦,但仍能实现对目标的成像。当OD= 1,Albedo=0.1时,能实现对目标的成像。随着光学厚度的增加和单次散射反照率的增加,发现传统的空空TR-MUSIC不能实现对目标的成像。由此可知当OD=0.1时,表示随机介质的影响较小,接近于自由空间。当OD=5时,表示随机介质的影响较大。光学厚度越大,单次散射反照率越大,表示随机介质对目标成像的影响越严重。

|
Download:
|
| 图 6 不同随机介质参数下空空TR-MUSIC成像仿真结果 Fig. 6 Space-space TR-MUSIC simulation results under different parameters of random media | |
空频TR-MUSIC对随机介质背景下目标成像,光学厚度与单次散射反照率与空空TR-MUSIC对随机介质背景下目标的成像参数设置相同:OD=0.1,1,5,Albedo=0.1,0.5,1。从图 7(a)可以看出当OD为0.1时,虽然随着Albedo的增加,图像点变大,聚焦效果变差,但是与空空TR-MUSIC相比,其变化较小。当OD=1时,随着Albedo的增加,图像的纵向聚焦性能明显变差。当OD=5,Albedo=0.5和1时,虽然空频TR-MUSIC在方位向和距离向均出现较为严重的散焦现象,但其成像效果仍优于空空TR-MUSIC。为进一步验证空频TR-MUSIC,给出载频为24 GHz时的成像结果图 7(b),与图 7(a)对比可知:当OD=0.1,1时,随机介质的影响较弱。随着频率的增加,波长变短,电磁波穿过随机介质的能力减弱,导致距离向分辨率明显变差;当OD=5,Albedo=1时,随机介质的影响较强,因此频率增加对成像结果影响较小。

|
Download:
|
| 图 7 不同随机介质参数下空频TR-MUSIC成像仿真结果 Fig. 7 Space-frequency TR-MUSIC simulation results under different parameters of random media | |
经对比可知,在相同的光学厚度和单次散射反照率条件下,空频TR-MUSIC成像效果较好。本文利用距离向3 dB波束宽度、方位向3 dB波束宽度对空频TR-MUSIC成像结果进行定量评价。由图 8(a)可知,距离向分辨率受随机介质的影响较大,其值约为方位向分辨的10倍。当Albedo=0.1时,方位向分辨率受OD的影响较小,当Albedo=0.5,1时,其受OD的影响较大,值呈现阶梯式增长。当Albedo=0.1时,距离向分辨率与OD呈近似线性关系,当Albedo=0.5,1时,其值先随OD迅速增加,后趋于平稳。

|
Download:
|
| 图 8 空频TR-MUSIC成像效能评估 Fig. 8 Evaluation of space-frequency TR-MUSIC imaging performance | |
光学厚度和单次散射反照率均是影响随机介质背景下目标成像效能的主要因素。通过观察可发现,OD=1,Albedo=0.5和OD=5,Albedo=0.1具有相同的成像结果,OD=1,Albedo=0.1与OD=0.1,Albedo=1也具有相同的现象。以上二者均有一个共同的条件即散射厚度相同。由此分别考虑散射厚度和吸收厚度对成像结果的影响。当Albedo=1时表示只考虑随机介质对电磁波的散射作用,而不考虑吸收作用,Albedo=0时会导致式(23)中存在分母为0的现象,因此用Albedo=0.1近似表示电磁波在穿过随机介质时仅考虑吸收作用,而不考虑吸收作用。为进一步研究吸收厚度对随机介质背景下目标成像的影响,将散射厚度设置为定值1,仅改变吸收厚度。由图 8(b)可知,距离向和方位向分辨率均不受吸收厚度的影响,仅随散射厚度的增加而降低。造成此现象的原因是当散射厚度较大时,电磁波在传播时受到随机介质的影响较大,较多的能量被散射,使得来自随机介质的影响增强,导致目标的成像效果变差。
从以上仿真结果图可以看出,空空TR-MUSIC对随机介质背景下目标的成像效果较差,易受杂波的影响,成像的稳定性和抗噪性较差。而空频TR-MUSIC成像受随机介质的影响较小,具有较好的成像分辨率。
3 结论本文提出基于空频分解TR-MUSIC成像新方法,利用阵列接收到的散射场数据建立空频多态数据矩阵,对矩阵进行奇异值分解得左奇异矢量,将组成噪声子空间的左奇异向量与发射信号的频谱信息结合作为时间反转信号,从而实现对目标的成像。从信号处理的角度而言,对于自由空间中的目标成像,新方法具有更好的聚焦效果,分辨率更好。传统的空空TR-MUSIC成像受随机介质的影响较大,从而不能实现对较大散射厚度的随机介质背景下目标的准确成像,成像方法的抗噪性能较差;而新方法的抗噪性能较强,受随机介质的影响较弱,能实现对复杂环境下目标的成像。在不同光学厚度以及单次散射反照率的情况下,空频TR-MUSIC表现较好,而空空TR-MUSIC表现较差。散射厚度是造成成像效果退化的主要原因。当为获得的散射场数据叠加信噪比为-10 dB的高斯白噪声时,传统的空空TR-MUSIC成像方法几乎失败,虽然纵向成像峰值存在偏移和图像斑点较大,但空频TR-MUSIC能实现对目标的聚焦。当叠加信噪比为10 dB的高斯白噪声时,空空TR-MUSIC不能实现对目标的聚焦成像,而空频TR-MUSIC能实现对目标的准确成像。
| [1] |
Fink M. Time reversed acoustics[J]. Physics Today, 1997, 50(3): 34-40. Doi:10.1063/1.881692 |
| [2] |
常敬明, 金铭, 曾江源, 等. 随机介质场景下的时间反转成像效果分析[J]. 中国科学院大学学报, 2018, 35(1): 59-65. |
| [3] |
Ishimaru A, Jaruwatanadilok S, Kuga Y. Time reversal effects in random scattering media on superresolution, shower curtain effects, and backscattering enhancement[J]. Radio Science, 2007, 42(6): 1-9. |
| [4] |
Liu D, Vasudevan S, Krolik J, et al. Electromagnetic time-reversal source localization in changing media: experiment and analysis[J]. IEEE Transactions on Antennas & Propagation, 2007, 55(2): 344-354. |
| [5] |
Lerosey G, Rosny J, Tourin A, et al. Time reversal of electromagnetic waves[J]. Physical Review Letters, 2004, 92(19): 193904. Doi:10.1103/PhysRevLett.92.193904 |
| [6] |
Oestges C, Kim A D, Papanicolaou G, et al. Characterization of space-time focusing in time-reversed random fields[J]. IEEE Transactions on Antennas & Propagation, 2005, 53(1): 283-293. |
| [7] |
Shi G, Nehorai A. A relationship between time-reversal imaging and maximum-likelihood scattering estimation[J]. IEEE Transactions on Signal Processing, 2007, 55(9): 4707-4711. Doi:10.1109/TSP.2007.896244 |
| [8] |
Prada C, Fink M. Eigenmodes of the time reversal operator: a solution to selective focusing in multiple-target media[J]. Wave Motion, 1994, 20(2): 151-163. Doi:10.1016/0165-2125(94)90039-6 |
| [9] |
Prada C, Manneville S B, Spoliansky D, et al. Decomposition of the time reversal operator: detection and selective focusing on two scatterers[J]. Journal of the Acoustical Society of America, 1996, 99(4): 2067-2076. Doi:10.1121/1.415393 |
| [10] |
Lev-ari H, Devancy A J. The time-reversal technique re-interpreted: subspace-based signal processing for multi-static target location[C]//proceedings of the Proceedings of the 2000 IEEE Sensor Array and Multichannel Signal Processing Workshop SAM 2000(Cat No 00EX410). IEEE, 2000: 509-513.
|
| [11] |
Devaney A J. Time reversal imaging of obscured targets from multistatic data[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(5): 1600-1610. Doi:10.1109/TAP.2005.846723 |
| [12] |
Yousefnia M, Ebrahimzadeh A, Dehmollaian M, et al. A time-reversal imaging system for breast screening: theory and initial phantom results[J]. IEEE Transactions on Biomedical Engineering, 2018, 65(11): 2542-2551. Doi:10.1109/TBME.2018.2807799 |
| [13] |
Yavuz M E, Teixeira F L. On the sensitivity of time-reversal imaging techniques to model perturbations[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(3): 834-843. Doi:10.1109/TAP.2008.916933 |
| [14] |
Ishimaru A, Jaruwatanadilok S, Kuga Y. Imaging through random multiple scattering media using integration of propagation and array signal processing[J]. Waves in Random & Complex Media, 2012, 22(1): 24-39. |
| [15] |
夏云龙, 付永庆. 一种随机媒质时间反转成像算法[J]. 信息技术, 2006, 30(5): 70-71. |
| [16] |
Bagherkhani S, Faraji-dana R, Dehmollaian M. A time-reversal imaging system for buried objects in layered media using complex images Green's functions[J]. AEU-International Journal of Electronics and Communications, 2019, 105: 1-8. Doi:10.1016/j.aeue.2019.03.019 |
| [17] |
Scholz B. Towards virtual electrical breast biopsy: space-frequency MUSIC for trans-admittance data[J]. IEEE Transactions on Medical Imaging, 2002, 21(6): 588-595. Doi:10.1109/TMI.2002.800609 |
| [18] |
Yavuz M E, Teixeira F L. Space-frequency ultrawideband time-reversal imaging[J]. IEEE Transactions on Geoscience & Remote Sensing, 2008, 46(4): 1115-1124. |
| [19] |
钟选明, 廖成, 冯菊. 基于空谱分解的时间反演时域成像[J]. 电波科学学报, 2014, 29(3): 476-479, 491. |
| [20] |
Zhong X, Liao C, Lin W. Space-frequency decomposition and time-reversal imaging[J]. IEEE Transactions on Antennas & Propagation, 2015, 63(12): 5619-5628. |
| [21] |
Ishimaru A. Wave propagation and scattering in random media. Repr. of the 1978 orig[J]. Wave Propagation & Scattering in Random Media, 1978, 1(6): 407-460. |
| [22] |
Goodman J W. Statistical optics[M]. New York: John Wiley Press, 1985: 550-570.
|
| [23] |
Chan T, Jaruwatanadilok S, Kuga Y, et al. Numerical study of the time-reversal effects on super-resolution in random scattering media and comparison with an analytical model[J]. Waves in Random & Complex Media, 2008, 18(4): 627-639. |
 2021, Vol. 38
2021, Vol. 38 


