在大规模多输入多输出(massive multi-input multi-output, MIMO)系统中,通过在收发端部署大量的天线,可以大幅提高系统吞吐量。因此大规模MIMO技术被认为是第5代移动通信系统(5G)的重要组成部分[1]。近年来,基于毫米波(mmWave)的移动通信系统受到研究者和工程师的广泛关注。相比于低频段的电磁波,毫米波的特点是频率较高,能够带来极大的带宽提升;另外其波长较短,使得系统的天线尺寸大大减小。对于毫米波大规模MIMO系统,物理尺寸较小的阵列中可以封装数百根天线,具备服务大量用户的能力。
在传统的MIMO通信系统中,为消除数据流之间的干扰,提升系统传输性能,需要对基带信号做波束成形(beamforming)处理[2]。常见的波束成形技术包括最大比传输(maximum ratio tranmission, MRT)、迫零(zero forcing, ZF)和块对角化(block diagonalization, BD)等[1]。这类数字波束成形方案,需要为每根天线配置一条射频(radio frequency, RF)链路。而对于毫米波大规模MIMO系统,大量的RF链路将造成昂贵的硬件成本和过高的能耗,因此全数字的方案不再适用。
为了以合理的硬件复杂度和能量损耗达到较为满意的频谱效率,一种数字/模拟混合波束成形(hybrid beamforming, HBF)方案被提出。HBF最早作为一种“天线软选择”方案被引入毫米波通信系统[3]。其主要思想是将传统的全数字波束成形器(beamformer)分为一个低维度的数字波束成形器和一个模拟波束成形器。其中数字波束成形器由少量的RF链路实现,模拟波束成形器由一个模拟移相器网络实现。总的来说,现有两种被广泛认可的HBF硬件架构:全连接架构[4-10]和部分连接架构[11-14]。
对于全连接架构,每个RF链路通过移相器网络和阵列中每个天线元素相连接。因此,在全连接架构中每个RF链路可以获得全阵列增益。文献[4-6]研究单用户MIMO下的HBF问题。对于多用户MIMO的场景,文献[7]研究上行链路中的HBF设计以及基站端的天线选择问题。文献[8]利用下行链路中基站(base station, BS)到多个用户的组合信道矩阵共轭转置后的相位来更新模拟波束成形矩阵, 这是一个充分利用大规模MIMO阵列增益的十分简单有效的方法,但文献[8]仅考虑配置单天线的用户。文献[9-10]考虑用户配置多天线的情况。其中文献[9]考虑每个用户仅配置一个RF链路,因此只需设计模拟接收器(combiner),无需设计数字接收器,并且每个用户只能接收一个数据流。文献[10]考虑用户配置多个RF链路以支持多流传输, 提出一种混合块对角化(hybrid-BD)方案设计收发端的波束成形矩阵。但是文献[10]所提算法要求所有用户配置的RF链路数之和等于基站配置的RF链路数。
全连接架构需要大量的移相器,这使得系统能耗依然较大。因此一种部分连接的架构被提出[11]。部分连接架构中,每条RF链路仅和阵列中的一部分天线元件相连接,因此硬件上更易于实现。事实上,这种部分连接架构已经被应用于3GPP LTE系统(其中每条RF链路连接8根天线)。另一方面,这种部分连接架构将引入更多的约束,使得波束成形算法更加复杂。文献[12]考虑点对点场景中,部分连接架构下的HBF问题;它通过将问题转化为一个每天线功率约束的单流最佳波束成形问题来求解。文献[13-14]研究部分连接架构下的HBF问题,但没有考虑用户端的设计。文献[15]基于串行干扰消除(serial interference canceller, SIC)的思想,提出逐个设计子阵列的波束成形矩阵的迭代算法,但是因为这种算法中各个子阵列的波束成形矩阵是单独设计的,其数字波束成形矩阵被约束为实数对角矩阵,这造成了一部分波束成形增益的损失。
本文研究多用户毫米波大规模MIMO系统中下行HBF问题。基站端部署部分连接的HBF架构。为了支持多流传输,每个用户配置多根天线和多条RF链路。因此发送端和接收端都需要HBF的设计。据我们所知,在具有部分连接架构的多用户毫米波MIMO系统中,很少有文献同时考虑发送端和接收端的混合波束成形设计。
为了得到更好的性能,本文考虑不在用户端采用波束选择的方案[10],而是联合优化基站端和用户端的波束成形矩阵。本文将该HBF问题解耦为两个阶段:模拟波束成形阶段和数字波束成形阶段。在第1阶段,提出一个基于稀疏主成分分析的算法来获取部分连接阵列的模拟波束成形矩阵,并联合优化基站和用户的模拟波束成形矩阵。在第2阶段,为了联合优化基站和用户的数字波束成形矩阵,将系统和速率最大化的问题转化为一个加权均方误差最小化(weighted minimum mean square error, WMMSE)问题,并利用块坐标下降算法解决。相比于现有的方案[10, 15],本文所提方案不需要在用户数或者数字波束成形矩阵的结构上有额外的约束条件,这将给系统设计带来极大的便利。仿真结果显示本文所提方案在频谱效率上表现出较高的性能,而且系统能耗大幅度降低。
1 系统模型 1.1 系统模型如图 1所示,考虑一个多用户毫米波大规模MIMO系统下行链路,基站和K个用户都部署了混合波束成形的硬件架构。假设基站一共配置了Mt根天线和Nt条RF链路。每个用户配置了Mr根天线和Nr条RF链路。

|
Download:
|
| 图 1 系统模型 Fig. 1 System model | |
在混合波束成形架构下,待发送信号首先经过一个维度为Nt×Ns的数字预编码器V,然后经过一个维度为Mt×Nt的模拟预编码器B。由于模拟预编码器是由移相器网络来实现,只能对信号的相位进行处理,因此对于矩阵B,有恒定模值约束:|B(i, j)|=
一共有
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{BVs}}, $ | (1) |
其中:s=[s1T, …, sKT]T∈
| $ \begin{array}{c} \hat{\boldsymbol{s}}_{k}=\underbrace{\boldsymbol{W}_{k}^{\mathrm{H}} \boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{H}_{k} \boldsymbol{B} \boldsymbol{V}_{k} \boldsymbol{s}_{k}}_{\text {所需信号 }}+\underbrace{\boldsymbol{W}_{k}^{\mathrm{H}} \boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{H}_{k} \boldsymbol{B} \sum\limits_{j=1, j \neq k}^{K} \boldsymbol{V}_{j} \boldsymbol{s}_{j}}_{\text {干扰 }}+ \\ \underbrace{\boldsymbol{W}_{k}^{\mathrm{H}} \boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{n}_{k}}_{\text {噪声 }},\end{array} $ | (2) |
其中:
因为RF链路的成本较高,在混合波束成形架构中一般RF链路数小于天线数,即Nt < Mt,Nr < Mr。为了减少硬件复杂度和能耗,本文考虑基站端部署部分连接的HBF硬件架构。每条RF链路将连接Ma=Mt/Nt根天线。假设第j条RF链路和第i根天线相连接,那么对应的会有B(i, j) 元素为非零值。否则,有B(i, j)=0,{i, j}∉Ψ,其中Ψ表示矩阵B中具有非零元素的索引集合。完整的模拟预编码矩阵可以表达为
| $ \boldsymbol{B}=\left[\begin{array}{cccc} \boldsymbol{b}_{1} & 0 & \cdots & 0 \\ 0 & \boldsymbol{b}_{2} & 0 & \vdots \\ \vdots & 0 & \ddots & 0 \\ 0 & \cdots & 0 & \boldsymbol{b}_{N_{t}} \end{array}\right]. $ | (3) |
对于用户k,其频谱效率可以表达为
| $ \begin{array}{l} R_{k}= \\ \log _{2}\left(\left|\boldsymbol{I}_{N_{\mathrm{s}}^{(k)}}+\boldsymbol{W}_{k}^{\mathrm{H}} \boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{H}_{k} \boldsymbol{B} \boldsymbol{V}_{k} \boldsymbol{V}_{k}^{\mathrm{H}} \boldsymbol{B}^{\mathrm{H}} \boldsymbol{H}_{k}^{\mathrm{H}} \boldsymbol{F}_{k} \boldsymbol{W}_{k} \overline{\boldsymbol{\varOmega}}_{k}^{-1}\right|\right), \end{array} $ | (4) |
其中: Ωk表示即时干扰加噪声协方差矩阵,其表达式为
| $ \overline{\boldsymbol{\varOmega}}_{k}=\boldsymbol{W}_{k}^{\mathrm{H}}\left(\boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{H}_{k} \boldsymbol{B} \sum\limits_{j \neq k}^{K} \boldsymbol{V}_{j} \boldsymbol{V}_{j}^{\mathrm{H}} \boldsymbol{B}^{\mathrm{H}} \boldsymbol{H}_{k}^{\mathrm{H}} \boldsymbol{F}_{k}+\boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{F}_{k} \boldsymbol{\delta}_{k}^{2}\right) \boldsymbol{W}_{k}, $ | (5) |
其中: nk~CN(0, δk2I) 为加性高斯白噪声向量。
1.2 信道模型考虑到高自由空间路径损耗和大型紧密封装的天线阵列,在大规模MIMO系统中的毫米波传播特征可以使用有限的空间选择或散射模型刻画,比如Saleh-Valenzuela模型。在Saleh-Valenzuela模型中,信道矩阵是Ncl个散射簇的贡献之和,其中每个散射簇中有Nray个传播路径。因此对于用户k,其信道矩阵Hk可以表达为
| $ \boldsymbol{H}_{k}=\sqrt{\frac{M_{\mathrm{t}} M_{\mathrm{r}}}{N_{\mathrm{cl}} N_{\mathrm{ray}}}} \sum\limits_{i=1}^{N_{\mathrm{cl}}} \sum\limits_{l=1}^{N_{\mathrm{ray}}} \alpha_{i l}^{(k)} \boldsymbol{a}_{\mathrm{r}}^{(k)}\left(\phi_{i l}^{(k)}\right) \boldsymbol{a}_{\mathrm{t}}^{(k)}\left(\theta_{i l}^{(k)}\right)^{\mathrm{H}}, $ | (6) |
其中:αil(k)表示该用户k第i个散射簇中第l个传播路径的增益,假设αil(k)为独立同分布的复高斯随机变量;ar(k)(ϕil(k))和at(k)(θil(k)) 分别为接收和发送阵列响应矢量,其中ϕil(k)、θil(k)分别为到达角(angle of arrival,AoA)、出发角(angle of departure,AoD)。在本文中,考虑均匀线性阵列天线(uniform linear array,ULA),因此阵列响应矢量可以表达为
| $ {\mathit{\boldsymbol{a}}^{{\rm{ULA}}}}(\phi ) = \frac{1}{{\sqrt M }}{\left[ {1,{{\rm{e}}^{{\rm{j}}\frac{{{\rm{2 \mathsf{ π} }}}}{\lambda }d\sin (\phi )}}, \cdots ,{{\rm{e}}^{{\rm{j}}(M - 1)\frac{{{\rm{2 \mathsf{ π} }}}}{\lambda }d\sin (\phi )}}} \right]^{\rm{T}}}, $ | (7) |
其中: ϕ表示出发/到达角,M为发送/接收天线,λ为波长,d表示天线间距。
2 收发端联合混合波束成形设计本文考虑系统同时服务K个用户,每个用户都支持多流传输。为了最大化系统和速率,同时考虑由发送功率预算带来的约束条件,以及由模拟移相器网络引入的对波束成形矩阵结构的限制,待求解的优化问题如表达式(8)所示。
问题(8)中Rk的表达式由式(4)给出,Pt为发送功率预算,Ψ为矩阵B中非零元素的索引集合。这里假定用户端部署全连接的硬件架构,因为相比于基站端,用户端的天线数量往往较小,这样的设定是合理的。
| $ \begin{array}{ll} \max \limits_{\boldsymbol{V}, \boldsymbol{B}, \boldsymbol{F}_{k}, \boldsymbol{W}_{k}, \forall k} & \sum\limits_{k=1}^{K} R_{k} \\ \text { s.t. } & \operatorname{tr}\left(\boldsymbol{B} \boldsymbol{V} \boldsymbol{V}^{\mathrm{H}} \boldsymbol{B}^{\mathrm{H}}\right) \leqslant P_{\mathrm{t}} \\ |\boldsymbol{B}(i, j)|=\frac{1}{\sqrt{M_{\mathrm{a}}}}, & \{i, j\} \in \varPsi \\ \boldsymbol{B}(i, j)=0, & \{i, j\} \notin \varPsi \\ \left|\boldsymbol{F}_{k}(i, j)\right|=\frac{1}{\sqrt{M_{\mathrm{r}}}}, & \forall\{i, j\}, k. \end{array} $ | (8) |
注意到问题(8)是没有直解的,一个简单有效的方法是将该HBF问题解耦为两个阶段,即首先进行模拟部分的设计,然后进行数字部分的设计[5]。在第1阶段,将联合设计发送和接收端的模拟波束成形矩阵,目的在于充分利用大规模MIMO系统的阵列增益。第2阶段,为了减少不同数据流之间的干扰并利用空间复用增益,将问题转化为一个加权均方误差最小化问题,联合优化发送和接收端的数字波束成形矩阵。
2.1 模拟波束成形设计为了最大化用户的可达速率,对于每个用户k,定义如下的等效信道矩阵
| $ {\mathit{\boldsymbol{\bar H}}_k} = \mathit{\boldsymbol{F}}_k^{\rm{H}}{\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{B}}. $ | (9) |
在第1阶段,本文尝试最大化上述的等效信道增益,以联合设计收发端的模拟波束成形矩阵。待求解的问题可以表达为
| $ \begin{array}{ll} \max \limits_{\boldsymbol{B}, \boldsymbol{F}_{k}, \forall k} & \sum\limits_{k=1}^{K}\left\|\boldsymbol{F}_{k} \boldsymbol{H}_{k} \boldsymbol{B}\right\|_{F}^{2} \\ \text { s.t. } & |\boldsymbol{B}(i, j)|=\frac{1}{\sqrt{M_{\mathrm{a}}}},\{i, j\} \in \varPsi \\ & \boldsymbol{B}(i, j)=0,\{i, j\} \notin \varPsi \\ & \left|\boldsymbol{F}_{k}(i, j)\right|=\frac{1}{\sqrt{M_{\mathrm{r}}}}, \forall\{i, j\}, k. \end{array} $ | (10) |
该问题是一个非凸问题,因此无法利用传统的优化方法求解。注意到矩阵B为具有式(3)所示结构的块对角矩阵,因此可以视作一个稀疏矩阵处理。在这一小节,提出一个基于稀疏主成分分析的方法来构建具有稀疏特性的矩阵B。利用交替优化的思想,矩阵B和矩阵Fk, ∀k将被迭代地更新。
根据线性代数,式(10)中的目标函数可以写为
| $ \begin{array}{l} \sum\limits_{k=1}^{K}\left\|\boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{H}_{k} \boldsymbol{B}\right\|_{F}^{2}= \\ \sum\limits_{k=1}^{K} \operatorname{tr}\left(\boldsymbol{B}^{\mathrm{H}} \boldsymbol{H}_{k}^{\mathrm{H}} \boldsymbol{F}_{k} \boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{H}_{k} \boldsymbol{B}\right)=\operatorname{tr}\left(\boldsymbol{B}^{\mathrm{H}} \boldsymbol{P} \boldsymbol{B}\right)= \\ \sum\limits_{k=1}^{K} \operatorname{tr}\left(\boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{H}_{k} \boldsymbol{B} \boldsymbol{B}^{\mathrm{H}} \boldsymbol{H}_{k}^{\mathrm{H}} \boldsymbol{F}_{k}\right)=\operatorname{tr}\left(\sum\limits_{k=1}^{K} \boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{Q}_{k} \boldsymbol{F}_{k}\right). \end{array} $ | (11) |
其中:矩阵P和矩阵Qk分别定义为
| $ \begin{array}{l} \boldsymbol{P}=\sum\limits_{k=1}^{K} \boldsymbol{H}_{k}^{\mathrm{H}} \boldsymbol{F}_{k} \boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{H}_{k}, \\ \boldsymbol{Q}_{k}=\boldsymbol{H}_{k} \boldsymbol{B} \boldsymbol{B}^{\mathrm{H}} \boldsymbol{H}_{k}^{\mathrm{H}} . \end{array} $ | (12) |
根据文献[5],假定矩阵B和矩阵Fk, ∀k为半酉(semi-unitary)矩阵,满足如下等式
| $ \boldsymbol{B}^{\mathrm{H}} \boldsymbol{B}=\boldsymbol{I}_{N_{\mathrm{t}}}, \boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{F}_{k}=\boldsymbol{I}_{N_{\mathrm{r}}}. $ | (13) |
对于大规模MIMO系统(天线数目较大),上述等式是渐近成立的。注意到矩阵P和矩阵Qk皆为埃尔米特(Hermitian)矩阵,因此如果暂时忽略问题(10)中的约束条件,最优矩阵的B和Fk可以通过交替对矩阵P和Qk求奇异值分解获取。
考虑到矩阵B的结构如式(3)所示,可以将其视为一个稀疏矩阵。对于给定的矩阵Fk, ∀k,为了构造稀疏矩阵B,只需找到矩阵P的前Nt个稀疏奇异向量即可。根据文献[16],这种问题可以转化为一个稀疏主成分分析问题,并利用相对应的算法求解。受到文献[16]的启发,可以利用稀疏主成分分析算法逐个恢复出矩阵B稀疏列向量。在初始阶段,仅考虑第一个子阵列,为了获取该子阵列对应的模拟波束成形向量,需要求解以下的稀疏主成分分析问题
| $ \begin{array}{l} \max \boldsymbol{x}_{1}^{\mathrm{H}} \boldsymbol{P} \boldsymbol{x}_{1} \\ \text { s.t. }\left\|\boldsymbol{x}_{1}\right\|_{2}=1,\left\|\boldsymbol{x}_{1}\right\|_{0}=M_{\mathrm{a}} . \end{array} $ | (14) |
其中: x1为一个稀疏向量,表示矩阵B的第一列。其中的ϑ0范数约束确保仅有Ma根天线和第一条RF链路连接。在本文的场景下,列向量x1具有固定的稀疏模式,并从矩阵P中得以恢复。如表 1所示,在得到x1后,矩阵P经过更新以在下一步恢复稀疏向量x2。矩阵Y为一个稀疏矩阵,指定RF链路和天线阵列之间的连接关系,因此Y满足Y(i, j)=1, ∀{i, j}∈Ψ。在算法中Y (n) 表示矩阵Y的第n列,⊙表示矩阵Hadamard积。
|
|
表 1 基于稀疏PCA的模拟波束成形算法流程 Table 1 Sparse PCA-based algorithm for analog beamforming |
由于用户端部署全连接架构,矩阵Fk, ∀k可以通过对Qk, ∀k奇异值分解来更新。联合设计收发端波束成形矩阵的完整算法如表 2所示。
|
|
表 2 收发端联合的模拟波束成形算法流程 Table 2 Algorithm for joint analog beamforming design |
本小节尝试联合优化收发端的数字波束成形矩阵。给定模拟预编码和接收矩阵,对应的数字预编码和接收矩阵Vk,Wk, ∀k,可以在等效信道矩阵Hk=FkHHkB, ∀k基础上计算。优化问题(8)可以重写为
| $ \begin{aligned} \max \limits_{\boldsymbol{V}_{k}, \boldsymbol{W}_{k}, \forall k} & \sum\limits_{k=1}^{K} \log _{2}\left(\left|\boldsymbol{I}_{N_{\mathrm{s}}^{(k)}}+\boldsymbol{W}_{k}^{\mathrm{H}} \overline{\boldsymbol{H}}_{k} \boldsymbol{V}_{k} \boldsymbol{V}_{k}^{\mathrm{H}} \overline{\boldsymbol{H}}_{k}^{\mathrm{H}} \boldsymbol{W}_{k} \overline{\boldsymbol{\varOmega}}_{k}^{-1}\right|\right) \\ & \text {s.t. } \sum\limits_{k=1}^{K} \operatorname{tr}\left(\boldsymbol{B} \boldsymbol{V}_{k} \boldsymbol{V}_{k}^{\mathrm{H}} \boldsymbol{B}^{\mathrm{H}}\right) \leqslant P_{\mathrm{t}}. \end{aligned} $ | (15) |
上述问题(15)是一个非凸问题。为解决该问题,首先定义以下的均方误差矩阵
| $ \begin{aligned} \boldsymbol{E}_{k}=& \mathbb{E}\left[\left(\hat{\boldsymbol{s}}_{k}-\boldsymbol{s}_{k}\right)\left(\hat{\boldsymbol{s}}_{k}-\boldsymbol{s}_{k}\right)^{\mathrm{H}}\right] \\ =& \boldsymbol{W}_{k}^{\mathrm{H}}\left(\overline{\boldsymbol{H}}_{k} \boldsymbol{V}_{k} \boldsymbol{V}_{k}^{\mathrm{H}} \overline{\boldsymbol{H}}_{k}^{\mathrm{H}}+\boldsymbol{\varOmega}_{k}\right) \boldsymbol{W}_{k}+\boldsymbol{I}_{d k} \\ & \boldsymbol{V}_{k}^{\mathrm{H}} \overline{\boldsymbol{H}}_{k}^{\mathrm{H}} \boldsymbol{W}_{k}-\boldsymbol{W}_{k}^{\mathrm{H}} \overline{\boldsymbol{H}}_{k} \boldsymbol{V}_{k}, \end{aligned} $ | (16) |
其中,矩阵Ωk定义为
| $ \boldsymbol{\varOmega}_{k}=\overline{\boldsymbol{H}}_{k} \sum\limits_{j \neq k}^{K} \boldsymbol{V}_{j} \boldsymbol{V}_{j}^{\mathrm{H}} \overline{\boldsymbol{H}}_{k}^{\mathrm{H}}+\boldsymbol{F}_{k}^{\mathrm{H}} \boldsymbol{F}_{k} \boldsymbol{\delta}_{k}^{2}. $ | (17) |
对于问题(15),有以下定理[17]
定理1:式(18)中所示的WMMSE问题的最优解能够为式(15)的最大和速率问题提供一个下界
| $ \begin{aligned} \min _{\boldsymbol{A}_{k}, \boldsymbol{W}_{k}, \boldsymbol{V}_{k}, \forall k} & \sum\limits_{k=1}^{K}\left(\operatorname{tr}\left(\boldsymbol{A}_{k} \boldsymbol{E}_{k}\right)-\log _{2}\left|\boldsymbol{A}_{k}\right|\right) \\ \text { s.t. } & \sum\limits_{k=1}^{K} \operatorname{tr}\left(\boldsymbol{B} \boldsymbol{V}_{k} \boldsymbol{V}_{k}^{\mathrm{H}} \boldsymbol{B}^{\mathrm{H}}\right) \leqslant P_{t}, \end{aligned} $ | (18) |
其中Ak≥0为一个Ns(k)×Ns(k)的权重矩阵。
问题(18)中的目标函数对所有自变量是非凸函数,但是若固定其中2个变量,对另一变量则是凸函数。基于交替优化的思想,本文提出一个块坐标下降算法求解问题(18),也即等效于求解优化问题(15)。
若固定权重矩阵Ak, ∀k和数字预编码矩阵Vk, ∀k,最优的数字接收矩阵可以通过一阶最优条件得到
| $ \boldsymbol{W}_{k}=\left(\overline{\boldsymbol{H}}_{k} \boldsymbol{V}_{k} \boldsymbol{V}_{k}^{\mathrm{H}} \overline{\boldsymbol{H}}_{k}^{\mathrm{H}}+\boldsymbol{\varOmega}_{k}\right)^{-1} \overline{\boldsymbol{H}}_{k} \boldsymbol{V}_{k}, \forall k. $ | (19) |
类似地,可以得到最优Ak,Vk表达式为
| $ \boldsymbol{A}_{k}=\left(\boldsymbol{I}_{d k}-\boldsymbol{V}_{k}^{\mathrm{H}} \overline{\boldsymbol{H}}_{k}^{\mathrm{H}} \boldsymbol{W}_{k}\right)^{-1}, \forall k, $ | (20) |
| $ \boldsymbol{V}_{k}=\left(\sum\limits_{j=1}^{K} \overline{\boldsymbol{H}}_{j}^{\mathrm{H}} \boldsymbol{W}_{j} \boldsymbol{A}_{j} \boldsymbol{W}_{j}^{\mathrm{H}} \overline{\boldsymbol{H}}_{j}+\lambda \boldsymbol{B}^{\mathrm{H}} \boldsymbol{B}\right)^{-1} \overline{\boldsymbol{H}}_{k}^{\mathrm{H}} \boldsymbol{W}_{k} \boldsymbol{A}_{k}, \forall k . $ | (21) |
其中λ为拉格朗日乘子,可以通过二分搜索得到。表 3展示了联合设计收发两端数字波束成形矩阵的完整算法。
|
|
表 3 收发端联合的数字波束成形算法流程 Table 3 Algorithm for joint digital beamforming design |
本节对所提的方案进行仿真性能验证,并与现有的HBF算法[10, 15],以及文献[2]所提的全数字块对角化算法进行对比。考虑基站配置Mt=256根天线,Nt=16条RF链路。每个用户配置Mr=8根天线,Nr=4条RF链路。假设一共有K=4个用户,每个用户需要接收4个数据流,基站需要同时传送
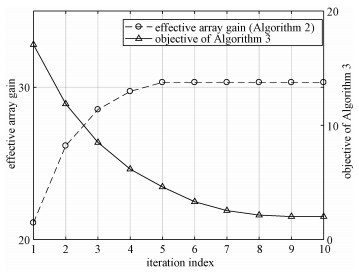
图 2对所提算法收敛性进行了验证。可以发现,在第1阶段,为了使式(9)所示的等效阵列增益最大化,本文所提的算法2能够在4~5次迭代后收敛;在第2阶段,利用算法3求解问题(18),目标函数在8~9次迭代后也基本收敛。总体而言,本文所提方案复杂度是可以接受的。而且通过收发端的协作,提高了系统对信道条件变化的适应性,提升了系统吞吐量。
|
Download:
|
| 图 2 算法收敛性评估 Fig. 2 Convergence of proposed algorithms | |
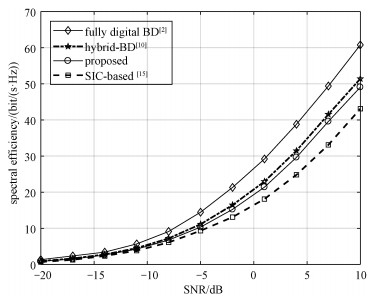
图 3展示所提方案在频谱效率上的性能表现。将文献[2]的全数字方案作为参考标准。可以发现,本文所提方案在频谱效率上的性能接近文献[10]所提的Hybrid-BD方案,而Hybrid-BD方案是部署在全连接的HBF架构上的。这是因为本文所提的算法充分利用了基站和用户之间的协作,提升波束成形的性能。另外,本文所提方案不需要对用户数进行约束,这有利于系统设计的灵活性。而Hybrid-BD方案必须满足Nt=KNr的条件。文献[15]所提的基于串行干扰消除(successive interference cancellation-based, SIC-based)的方案部署在部分连接的HBF架构上。可以发现本文所提方案频谱效率优于SIC-based方案。这是因为SIC-based方案要求数字波束成形矩阵为实数对角阵,这导致了部分的性能损失。
|
Download:
|
| 图 3 系统频谱效率与接收信噪比(SNR)的关系 Fig. 3 Spectral efficiency versus SNR | |
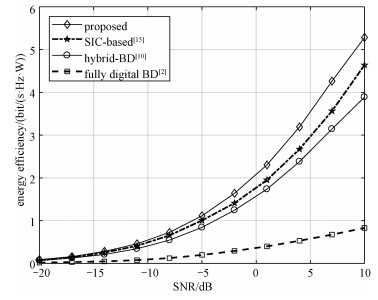
图 4展示不同方案在能量效率上的性能对比。参考文献[18],定义频谱效率表达式为
| $ \eta=\frac{R}{P_{\text {total }}}=\frac{R}{P_{\mathrm{t}}+N_{\mathrm{RF}} P_{\mathrm{RF}}+N_{\mathrm{PS}} P_{\mathrm{PS}}}. $ | (22) |
|
Download:
|
| 图 4 系统能量效率与接收信噪比(SNR)的关系 Fig. 4 Energy efficiency versus SNR | |
其中: Pt为发送功率; PRF为每条RF链路的消耗的功率,PPS为每个移相器消耗的功率; NRF,NPS分别为系统所需RF链路数量和移相器数量。本文设定PRF=250 mW,PPS=1 mW,Pt=1 W。从图中可以看到,本文所提方案能量效率显著优于其他3种方案。尽管Hybrid-BD方案在频谱效率上表现较好,但其能量效率偏低,这是因为全连接HBF架构需要大量移相器。对于配置Mt根天线、Nt条RF链路的基站,共需要MtNt个移相器,这大幅增加了系统能耗。全数字BD方案在能耗上表现最差,这也证明对于大规模MIMO系统而言,HBF是十分必要的。
4 结束语本文研究具有部分连接架构的多用户毫米波大规模MIMO系统中混合波束成形问题,提出一个联合设计收发端的数模混合波束成形的完整方案。为了联合优化基站端的模拟预编码矩阵和用户端的模拟接收矩阵,提出一个基于稀疏主成分分析的算法,最大化系统的等效信道增益。然后,将系统频谱效率最大化的问题转化为一个WMMSE问题,并利用块坐标下降算法联合优化数字预编码矩阵和接收矩阵。仿真结果显示本文所提方案的频谱效率性能优于部分连接架构下的其他方案,而且系统的能量效率与已有的HBF方案相比具有显著优势。
| [1] |
Molisch A F, Ratnam V V, Han S Q, et al. Hybrid beamforming for massive MIMO: a survey[J]. IEEE Communications Magazine, 2017, 55(9): 134-141. Doi:10.1109/MCOM.2017.1600400 |
| [2] |
Spencer Q H, Swindlehurst A L, Haardt M. Zero-forcing methods for downlink spatial multiplexing in multiuser MIMO channels[J]. IEEE Transactions on Signal Processing, 2004, 52(2): 461-471. Doi:10.1109/TSP.2003.821107 |
| [3] |
Zhang X Y, Molisch A F, Kung S Y. Variable-phase-shift-based RF-baseband codesign for MIMO antenna selection[J]. IEEE Transactions on Signal Processing, 2005, 53(11): 4091-4103. Doi:10.1109/TSP.2005.857024 |
| [4] |
Ayach O E, Rajagopal S, Abu-Surra S, et al. Spatially sparse precoding in millimeter wave MIMO systems[J]. IEEE Transactions on Wireless Communications, 2014, 13(3): 1499-1513. Doi:10.1109/TWC.2014.011714.130846 |
| [5] |
Sohrabi F, Yu W. Hybrid digital and analog beamforming design for large-scale antenna arrays[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(3): 501-513. Doi:10.1109/JSTSP.2016.2520912 |
| [6] |
Sohrabi F, Liu Y F, Yu W. One-bit precoding and constellation range design for massive MIMO with QAM signaling[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(3): 557-570. Doi:10.1109/JSTSP.2018.2823267 |
| [7] |
Zhai X F, Shi Q J, Cai Y L, et al. Joint transmit precoding and receive antenna selection for uplink multiuser massive MIMO systems[J]. IEEE Transactions on Communications, 2018, 66(11): 5249-5260. Doi:10.1109/TCOMM.2018.2854175 |
| [8] |
Liang L, Xu W, Dong X D. Low-complexity hybrid precoding in massive multiuser MIMO systems[J]. IEEE Wireless Communications Letters, 2014, 3(6): 653-656. Doi:10.1109/LWC.2014.2363831 |
| [9] |
Nguyen D H N, Le L B, Le-Ngoc T. Hybrid MMSE precoding for mmWave multiuser MIMO systems[C]//2016 IEEE International Conference on Communications (ICC). IEEE, 2016: 1-6.
|
| [10] |
Ni W H, Dong X D. Hybrid block diagonalization for massive multiuser MIMO systems[J]. IEEE Transactions on Communications, 2016, 64(1): 201-211. Doi:10.1109/TCOMM.2015.2502954 |
| [11] |
El Ayach O, Heath R W, Rajagopal S, et al. Multimode precoding in millimeter wave MIMO transmitters with multiple antenna sub-arrays[C]//2013 IEEE Global Communications Conference (GLOBECOM). IEEE, 2013: 3476-3480.
|
| [12] |
Li N X, Wei Z X, Yang H W, et al. Hybrid precoding for mmWave massive MIMO systems with partially connected structure[J]. IEEE Access, 2017, 5: 15142-15151. Doi:10.1109/ACCESS.2017.2720163 |
| [13] |
Yu X H, Zhang J, Letaief K B. Partially-connected hybrid precoding in mm-Wave systems with dynamic phase shifter networks[C]//2017 IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC). IEEE, 2017: 1-5.
|
| [14] |
Jin J N, Xiao C S, Chen W, et al. Hybrid Precoding in mmWave MIMO Broadcast Channels with Dynamic Subarrays and Finite-Alphabet Inputs[C]//2018 IEEE International Conference on Communications (ICC). IEEE, 2018: 1-6.
|
| [15] |
Gao X Y, Dai L L, Han S F, et al. Energy-efficient hybrid analog and digital precoding for mmWave MIMO systems with large antenna arrays[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(4): 998-1009. Doi:10.1109/JSAC.2016.2549418 |
| [16] |
Journée M, Nesterov Y, Richtárik P, et al. Generalized power method for sparse principal component analysis[J]. Journal of Machine Learning Research, 2010, 11(2): 517-553. |
| [17] |
Shi Q J, Razaviyayn M, Luo Z Q, et al. An iteratively weighted MMSE approach to distributed sum-utility maximization for a MIMO interfering broadcast channel[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4331-4340. Doi:10.1109/TSP.2011.2147784 |
| [18] |
Cui S G, Goldsmith A J, Bahai A. Energy-constrained modulation optimization[J]. IEEE Transactions on Wireless Communications, 2005, 4(5): 2349-2360. Doi:10.1109/TWC.2005.853882 |
 2021, Vol. 38
2021, Vol. 38 


