预冷是果蔬冷链物流体系中的关键环节。对采后果蔬快速进行预冷,能够在短时间内去除田间热,降低果蔬的呼吸强度,从而延长储存期和货架期[1]。在冷链流通过程中,未经预冷的果蔬质量损失比经过预冷的果蔬质量损失大约高23%[2]。差压预冷具有冷却速度快、效率高和成本低等优点,是目前应用最为广泛的预冷技术之一[3-4]。该技术利用风机产生必要的驱动力制造压差,迫使冷风通过包装箱的通风孔流经箱体内部,与果蔬直接进行热交换,从而达到快速预冷的目的[3]。
由气流的不均匀性导致的冷却异质性是差压预冷过程中的普遍现象。包装材料阻碍园艺产品和冷却气流的直接接触,因此增加了冷却气流的阻力和预冷过程的能耗[5-6]。同时,装有衬垫和果蔬的包装箱的复杂内部结构使得气流分布复杂化,导致严重的温度分布不均匀,出现局部过冷或局部冷却不足现象。这些异质性现象严重影响园艺产品的品质和货架寿命,也增加了预冷过程的能耗。
近20年来,为提高预冷效率,降低预冷能耗,相关学者开展了比较系统的研究。在预冷过程通风包装箱设计的早期研究中,实验测量占据主要地位。近年来,随着计算机技术的飞速发展,数值模拟已逐渐成为通风包装箱设计的替代研究方法。计算流体力学(computational fluid dynamics, CFD)由于其强大的模拟能力,不仅可以获得高时空分辨率的流场信息和温度分布,同时也能减少实验过程大量人力、物力的损耗[7-8]。通常,基于计算流体力学,差压预冷过程的数值方法可以分为两类:多孔介质方法和直接CFD模拟[9-10]。多孔介质方法通过将通风包装箱内部的复杂结构(如散装包装的产品空气区和分层包装的衬垫之间的区域)作为多孔介质来简化数学模型[11]。从而避免复杂的几何细节处理,大大减少了计算时间和仿真成本。但是多孔介质方法忽略了果蔬内部的温度梯度变化,并且当包装箱与果蔬的水力直径比小于10时,多孔介质内部的连续性假设不再成立[12]。直接CFD模拟在一定程度上克服了多孔介质假设的缺陷,能够精确地获取包装箱内部的空气流动和传热传质过程。虽然直接CFD模拟需要构建真实的复杂几何模型,提高了模型构建和网格划分的难度,增大了计算机资源的占用[9, 12]。但是随着计算机软硬件技术的提高,直接CFD模拟逐渐发展成为相关研究的主流方法。Zhao等[9]对两种数值模拟方法做了详细的介绍。
优化通风设计(通风孔面积、通风孔数量和通风孔位置)是提高预冷效率、降低预冷过程能耗的有效措施。其中,通风孔面积的影响最大[5-6]。随着通风孔面积的增加可提高冷却速率和冷却均匀性,降低气流阻力和预冷过程能耗[7, 13-15]。但是随着通风面积增加,冷却速率提高的幅度降低,并且考虑到增加通风孔面积对包装箱机械强度的负面影响,不同材料和用途的包装箱都有一个最佳的推荐通风孔面积比。例如,对于草莓,当通风孔面积比约为9.4%时,冷却均匀性最好[16]。Pathare等[17]对包装箱的通风孔设计做了详细总结。通风孔位置也是影响预冷效果的重要因素。如果通风孔的空间分布不合理,增加通风孔面积可能不会提高冷却速度[18]。已有研究结果[7]表明:均匀且对称分布的通风孔有利于多层通风包装箱的冷却均匀性,尤其是在处理3层以上包装时。在通风孔面积比一定的条件下,采用多孔设计也是提高冷却均匀性和降低能耗的一种有效途径[19]。除此之外,在流通过程中起防护作用的内部衬垫[20],也是影响包装箱内气流分布、冷却均匀性和能耗的重要因素[19]。Opara和Zou[21]研究衬垫与包装箱内壁之间的空隙宽度对预冷效果的影响。结果表明:果蔬中心温度对空隙宽度的变化非常敏感。最近,Gruyters等[22]采用直接CFD方法研究内部衬垫对包装箱内部气流分布和预冷效果的影响。结果表明:衬垫和通风孔位置之间的不匹配会导致冷却不均匀和高能耗。Han等[8]采用直接CFD方法,在考虑衬垫厚度及内部导热的前提下,对单侧开2孔的现有双层瓦楞包装箱进行优化设计,结果表明:单侧开4孔的包装箱不仅半冷却时间缩短了一半,冷却均匀性也有一定的提高。然而,他们并未研究衬垫对预冷效果的影响。根据作者掌握的文献资料,目前尚未见到有关内部衬垫优化设计的研究工作。
本文以单侧开2孔的现有双层瓦楞包装箱[8]为研究对象,采用直接CFD模拟方法建立三维计算模型。本研究着眼于衬垫设计对预冷过程的影响,重点研究衬垫与箱壁间空隙宽度对预冷时间和预冷均匀性的影响,以获取最佳空隙宽度为目标,为进一步优化层装包装箱、提高预冷效果提供理论依据。
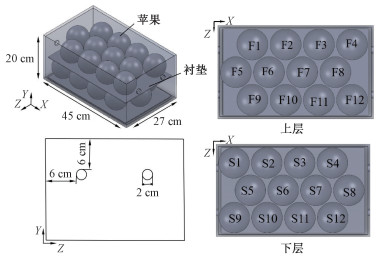
1 物理模型本文以目前市场上广泛使用的双层瓦楞苹果包装箱[8]为研究对象。图 1展示了双层瓦楞苹果包装箱的外形、尺寸和苹果的摆放方式。双层瓦楞苹果包装箱的尺寸为45 cm × 27 cm × 20 cm,壁面厚度为0.6 cm。在箱体的迎风侧和背风侧均有2个直径为2 cm的圆形通风孔,通风孔孔心距包装箱上表面和侧面的距离均为7 cm,通风孔开孔率为1.16%,具体位置如图 1所示。苹果在包装箱内部以交错的形式分两层摆放。上、下层之间用尺寸为42 cm × 25 cm × 0.3 cm的衬垫隔开。包装箱中共有24个苹果,每层12个。根据Han等[8]的研究,假设苹果直径为90 mm,平均重量为310 g。
|
Download:
|
| 图 1 双层瓦楞苹果包装箱及苹果摆放方式示意图 Fig. 1 Double-layered corrugated apple packaging box and stacked pattern of apples inside the box | |
衬垫与箱壁间空隙宽度是影响气流分布和预冷特性的重要因素, 其大小取决于包装箱和衬垫之间的尺寸差异。就双层瓦楞苹果包装箱而言,X方向的空隙宽度为9 mm,Z方向的空隙宽度为4 mm。本文研究衬垫与箱壁间空隙宽度增量ΔWgap在0~15 mm范围内变化时对苹果预冷效果的影响。其中,ΔWgap=0 mm对应目前市场上双层瓦楞苹果包装箱内部使用的标准衬垫。
2 数学模型 2.1 控制方程为降低计算成本,在构建数学模型的过程中引入以下简化假设[8, 23]:
1) 将单个苹果近似为球形;
2) 忽略呼吸热的影响,因为呼吸热仅占总热负荷的0.5%左右;
3) 空气、苹果、衬垫和瓦楞箱等所有物质的热物理性质与温度和湿度无关。其热物性参数由文献[8]得到,具体数值见表 1。
|
|
表 1 热物性参数 Table 1 Thermo-physical properties of substances |
参考已有的研究工作[8-9],把计算域划分为3个子区域:自由气流区、产品区(苹果)和固体区(箱壁和衬垫)。在预冷过程中,每个子区域的流动和传热特性满足下述控制方程:
1) 在自由气流区,速度场和温度场满足下面的连续性方程、动量方程和能量方程
| $ \frac{\partial \rho_{\mathrm{a}}}{\partial t}+\nabla \cdot\left(\rho_{\mathrm{a}} \boldsymbol{U}\right)=0 , $ | (1) |
| $ \begin{array}{c} \frac{{\partial \left( {{\rho _{\rm{a}}}\boldsymbol{U}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\rho _{\rm{a}}}\boldsymbol{UU}} \right) = - \nabla P + \nabla \cdot {\tau ^{(t)}} + {S_U} + \\ \nabla \cdot \left[ {{\mu _{\rm{a}}}\left( {\nabla \boldsymbol{U} + {{\left( {\nabla \boldsymbol{U}} \right)}^{\rm{T}}}} \right)} \right], \end{array} $ | (2) |
| $ \frac{\partial\left(\rho_{\mathrm{a}} c_{p, \mathrm{a}} \theta\right)}{\partial t}+\nabla \cdot\left(\rho_{\mathrm{a}} c_{p, \mathrm{a}} \boldsymbol{U} \theta\right)=\nabla \cdot\left(\lambda_{\mathrm{a}} \nabla \theta\right)-\nabla \cdot q^{(t)} . $ | (3) |
其中: 下标a代表空气; t为时间;U为速度矢量;θ为温度;P为压强;
2) 在产品区,考虑单个苹果内部的热传导过程,能量方程为
| $ \rho_{\mathrm{p}} c_{\mathrm{p}, p} \frac{\partial \theta_{\mathrm{p}}}{\partial t}=\lambda_{\mathrm{p}} \nabla^{2} \theta_{\mathrm{p}}+S_{\mathrm{e}} . $ | (4) |
其中: 下标p代表苹果,ρp为苹果密度;cp, p为苹果比热容;λp为苹果导热系数;θp为苹果温度; Se为能量源项,包括苹果的呼吸热、苹果表面的蒸腾热和冷凝热,考虑到Se在预冷环节对苹果冷却特性的影响很小,本文忽略此项。
3) 在固体区,能量方程的形式与产品区相同(如式(4)),衬垫(厚度为3 mm)和箱壁的热物性参数取表 1中的数值。
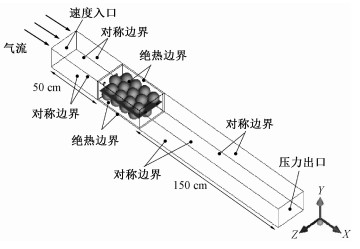
2.2 初始条件及边界条件为避免入口和出口边界对箱体附近气流的影响,分别在包装箱的迎风侧和背风侧增设长度为50 cm的入口段和长度为150 cm的出口段[7]。计算域的物理模型及边界条件如图 2所示。参考Han等[8]的研究工作,为保证通风孔处的平均气流速度为2 m/s,冷空气进口设置为低湍流强度(0.05%)的速度入口条件,送风速度为0.169 L/(s·kg),送风温度为2 ℃。冷空气出口为压力出口条件,压力设置为环境压力。包装箱的外壁设置为绝热壁面条件[24];考虑到苹果、衬垫及箱体内壁与冷空气之间的对流换热和导热,把交界面设置为耦合边界条件。入口段和出口段的侧面设置为滑移的对称边界,即:法向速度分量及其法向梯度均为零。苹果、衬垫及瓦楞箱初始温度均为27 ℃。
|
Download:
|
| 图 2 物理模型及边界条件 Fig. 2 The schematic diagram of the physical model and boundary conditions | |
参考现有的研究工作[6-8, 15, 19, 22, 25],综合考虑计算精度和计算量,开发了一种基于有限体积法的数值方案。首先,求解连续性方程和动量方程,获得气流分布的稳态解。然后,以稳态气流作为初始条件,求解非稳态的能量方程,获得瞬态的温度分布。基于时间敏感性分析,在瞬态计算过程中选择30 s的时间步长,每个时间步长迭代20步。采用SIMPLE算法解决压力-速度耦合问题。对流项的空间离散采用二阶迎风格式。与其他两方程湍流模型相比,采用SST κ-ω模型具有更好的收敛性和准确性;因此,本研究采用SST κ-ω模型解决雷诺时均方程的封闭问题。连续性方程、动量方程和湍流方程的收敛准则设置为10-3,能量方程的收敛准则设置为10-6。
网格划分是数值研究的重要环节,网格质量是影响数值结果准确度的关键因素。本研究使用ANSYS的预处理软件ICEM将图 2所示的计算域离散为四面体网格。在模型中考虑相邻苹果之间的空隙,在苹果表面生成精细网格,从而实现对黏性子层内流动和传热过程的精确求解。参考已有研究[8],利用网格扭曲率和y+两个参数检查网格质量。对3种不同的网格划分方案(网格数量分别为1 593 359,2 572 643和4 862 887)进行网格敏感性分析。与网格数量为1 593 359的模拟结果相比,采用网格数量为2 572 643的划分方案得到的质量流通速率、预冷时间及苹果表面切应力的相对偏差分别为1.28%、1.59%和2.52%;与网格数量为4 862 887的模拟结果相比,上述物理量的偏差分别为0.44%、1.15%和0.93%。因此,本文采用网格数量为2 572 643的划分方案,此时苹果内部网格最大尺寸为8 mm,通风孔处网格最大尺寸为5 mm,其他部分网格最大尺寸为10 mm。进一步,通过网格质量检查得出整体网格扭曲率和壁面y+值分别小于0.90和4.5。
3.2 算法检验为验证数值算法的可靠性,本文将双层瓦楞苹果包装箱内的模拟结果与Han等[8]的实验数据和模拟结果进行了定量的比较。Han等[8]的实验测试对象是F6和S6两个苹果的中心温度和表面温度,F6和S6的位置见图 1。本研究的模拟结果和Han等[8]的实验数据之间的温度偏差小于2.0 ℃。
为检验数值结果的准确性,使用均方根误差(root mean square error, RMSE)和平均相对偏差(average relative deviation, ARD)来衡量模拟值(Si)与实验值(Ei)的差异。RMSE和ARD通过式(5)和式(6)计算获得。从表 2可以看出,RMSE和ARD的最大值分别为1.778 ℃和7.76%。考虑到模型中的简化假设对模拟结果有一定影响,实验过程中实验条件、外界气温等因素对实验结果也有一些影响。我们认为本文的模拟结果与实验数据有较好的一致性。
|
|
表 2 本文模拟结果与文献[8]实验数据之间的偏差 Table 2 The deviation between the simulation results in this study and the existing experimental data in Ref.[8] |
| $ \operatorname{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(E_{i}-S_{i}\right)^{2}} , $ | (5) |
| $ \mathrm{ARD}=\frac{1}{n} \sum\limits_{i=1}^{n} \frac{\left|E_{i}-S_{i}\right|}{E_{i}} . $ | (6) |
产品的预冷时间通常利用式(7)定义的温度比Y来评估[7],
| $ Y = \frac{{{\theta _{\rm{p}}} - {\theta _{\rm{a}}}}}{{{\theta _{{\rm{pin}}}} - {\theta _{\rm{a}}}}}. $ | (7) |
其中: θp指所有苹果的平均温度,θa指冷空气的温度,θpin指苹果的初始温度。温度比是未完成的温度变化与特定条件下的总温度变化的比率。7/8预冷时间(seven-eights cooling time, SECT)是冷却到产品初始温度和气流温度差的7/8(Y=0.125)时所需的预冷时间,此时产品温度接近储藏所需温度,在此温度下将产品转移到储存设备中能够以较低的能源成本消除剩余的热负荷[25]。本文使用SECT评估预冷时间。
此外,还可以通过苹果表面的对流换热系数(convective heat transfer coefficient, CHTC)量化冷却速率[7]。计算公式为
| $ {\rm{CHTC}} = \frac{{{q_{{\rm{c, w}}}}}}{{{\theta _{\rm{w}}} - {\theta _{{\rm{ref}}}}}}. $ | (8) |
其中:qc, w是垂直于空气-产品交界面的对流热通量,θw是苹果表面温度。θref是参考温度,此处选用冷空气的入口温度。
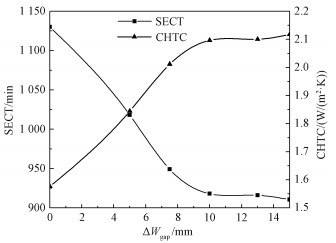
SECT和CHTC是衡量预冷速率的两个重要指标。随着衬垫与箱壁间空隙宽度的增加,SECT和此时苹果表面CHTC的变化如图 3所示,其中ΔWgap=0 mm对应双层瓦楞苹果包装箱内部使用的标准衬垫。随着衬垫与箱壁间空隙宽度的增加,在达到7/8预冷时间时,苹果表面的对流换热系数逐渐增大。这是因为随着衬垫与箱壁间空隙宽度的增加,流过下层苹果的冷空气量增加,强化了下层苹果与冷空气之间的对流换热。尤其是当ΔWgap < 10 mm时,随着ΔWgap的增加,CHTC明显增大,冷却速率显著提高。当采用现有衬垫(ΔWgap=0 mm)时,CHTC为1.577 W/(m2·K),当ΔWgap=10 mm时,CHTC增大到2.097 W/(m2·K),比采用现有衬垫增大32.98%。当ΔWgap>10 mm时,继续增大衬垫与箱壁间空隙宽度对冷却速率的影响不大。如图 3所示,SECT与CHTC呈现完全相反的变化趋势。这是因为随着衬垫与箱壁间空隙宽度增大,苹果表面的对流换热系数增大,单位时间内的换热量增加,使得苹果冷却到一定温度时的预冷时间缩短。当ΔWgap从0 mm增加到10 mm时,SECT从1 130 min减小到918 min,7/8预冷时间缩短18.76%。进一步增大ΔWgap,SECT的变化不再明显。因此,从提高冷却速率的角度考虑,最佳的空隙宽度增量为10 mm。
|
Download:
|
| 图 3 冷却速率参数(SECT和CHTC)随空隙宽度增量的变化 Fig. 3 Changes of cooling rate parameters (SECT and CHTC) with increment of gap width | |
预冷均匀性是影响果蔬品质的重要因素,提高预冷均匀性一直是通风包装设计的重要目标。图 4给出不同ΔWgap条件下得到的预冷300 min时的温度分布。从图中可以看出,无论是采用标准衬垫(ΔWgap=0 mm)还是适当增大衬垫与箱壁间的空隙宽度,冷却不均匀性都是普遍存在的现象,而且不同ΔWgap条件下的温度分布具有一定的相似性,即:上层苹果温度低于下层苹果温度,冷却不均匀性主要体现为上、下层苹果温度的差异。如图 4所示,采用标准衬垫(ΔWgap=0 mm) 的预冷均匀性最差,随着衬垫与箱壁间空隙宽度的增大,部分气流从上层苹果区流向下层苹果区,增强了下层苹果与冷空气之间的对流换热,使得下层苹果温度逐渐降低,而上层苹果温度略有升高。在ΔWgap≤10 mm条件下,增大空隙宽度,下层苹果温度降低明显。当ΔWgap>10 mm时,下层苹果的温度对空隙宽度的增加不再敏感。

|
Download:
|
| 图 4 预冷300 min时的温度分布 Fig. 4 Temperature distribution after 300 min of cooling | |
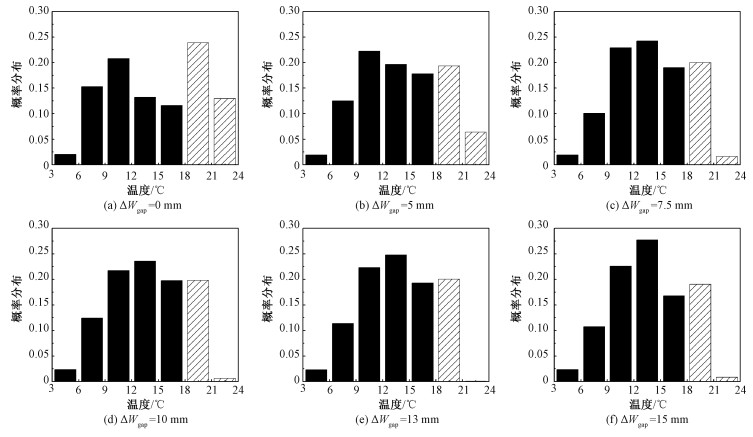
图 5给出预冷300 min时苹果温度的概率分布。结果显示,随着空隙宽度的增大,中间温区出现的概率逐渐增大,两个高温区(见图 5中斜线填充标记)在ΔWgap=0、5、7.5、10、13和15 mm条件下出现的概率分别为0.368 88、0.257 72、0.216 86、0.203 78、0.200 89和0.198 69。由此可见,增大空隙宽度能够降低出现局部高温区的概率,但是随着空隙宽度的增大,局部高温区出现概率的下降幅度逐渐减小。当ΔWgap=10 mm时,苹果温度在两个较高温度区间出现的概率比ΔWgap=0 mm降低44.76%。因此,增大衬垫与箱壁间空隙的宽度,能够显著降低局部高温区出现的概率,从而有效减缓果蔬的品质劣变。
|
Download:
|
| 图 5 预冷300 min时苹果温度的概率分布 Fig. 5 Probability distribution of apple temperature after 300 min of cooling | |
为更加准确地刻画衬垫与箱壁间空隙宽度的变化对预冷效果的影响,利用数理统计中反映数据离散程度的标准差量化预冷均匀性[20, 26],其计算公式为
| $ \sigma = \frac{1}{{\overline {{\theta _{\rm{p}}}} }}\sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {\left( {{\theta _{{\rm{p}}i}} - \overline {{\theta _{\rm{p}}}} } \right)} } . $ | (9) |
其中: σ为标准差;
图 6分别给出预冷300 min和7/8预冷时间时上、下层苹果温度差Δθ和标准差σ随衬垫与箱壁间空隙宽度增量ΔWgap的变化曲线,用于定量描述增大空隙宽度对预冷均匀性的影响。当预冷到300 min时,采用标准衬垫(ΔWgap=0 mm)时上、下层苹果的温度差Δθ和式(9)定义的标准差σ最高,分别为9.35 ℃和0.352,即:ΔWgap=0 mm时的预冷均匀性最差。随着ΔWgap的增大,下层苹果的温度逐渐降低(如图 4),因此Δθ和σ逐渐减小。当ΔWgap=5 mm时,Δθ和σ分别降至7.62 ℃和0.31。随着ΔWgap的进一步增大,两个指标降低的幅度逐渐减小,当ΔWgap>10 mm时,继续增大ΔWgap,预冷均匀性没有明显改善。
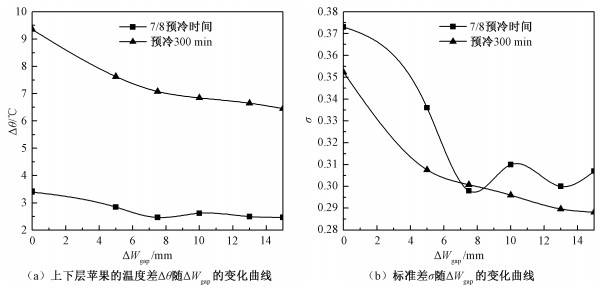
|
Download:
|
| 图 6 在预冷300 min和7/8预冷时间时不同ΔWgap条件下预冷均匀性的定量结果 Fig. 6 Quantitative results of precooling uniformity after 300 min and seven-eighths cooling time of cooling | |
在预冷结束(7/8预冷时间)时,ΔWgap=0 mm条件下的预冷均匀性仍然最差,此时Δθ和σ分别为3.39 ℃和0.373。当ΔWgap < 7.5 mm时,随着ΔWgap的增大,Δθ和σ均逐渐降低,预冷均匀性提高。当ΔWgap=7.5 mm时,Δθ和σ分别为2.46 ℃和0.298,比ΔWgap=0 mm时分别降低27.43%和20.11%。继续增大ΔWgap,Δθ和σ均有不同程度的波动,但是波动幅度逐渐降低。
综合考虑预冷中间过程(预冷300 min)和预冷结束(SECT)时ΔWgap对预冷均匀性的影响,最佳的空隙宽度增量为ΔWgap=7.5 mm,不仅能够保证在预冷结束时有最好的冷却均匀性,也可以保证在预冷过程中有较好的预冷均匀性。定量地讲,采用最佳方案(ΔWgap=7.5 mm)能够使上、下层苹果温度差Δθ在预冷300 min时和预冷结束时较现有方案(ΔWgap=0 mm)分别降低24.28%和27.43%。
5 结论如何提高预冷均匀性和预冷效率一直是果蔬预冷研究的一个热点问题。衬垫作为层装包装箱的重要组成部分,是造成不同层之间果蔬冷却异质性的重要因素。针对苹果在分层通风包装箱内的差压预冷过程,本文考虑衬垫厚度及内部传热的影响,建立了较完善的三维直接CFD模拟模型,在求解过程中采用半隐式SIMPLE算法和SST k-ω湍流模型。以目前市场上广泛使用的双层瓦楞苹果包装箱为研究对象,利用数值模拟结果,分析增大衬垫与箱壁间空隙的宽度对预冷时间和预冷均匀性的影响,得到以下结论:增大衬垫与箱壁间空隙宽度能够缩短预冷时间,提高预冷均匀性。随着空隙宽度的增大,预冷时间逐渐缩短,但预冷时间的变化幅度逐渐减小。当衬垫与箱壁间空隙宽度增量为10 mm(ΔWgap=10 mm)时,继续增加空隙宽度对预冷时间的影响不再显著。整体来看,增大ΔWgap能够提高预冷均匀性,但是当ΔWgap超过7.5 mm后,继续增大ΔWgap导致预冷结束时的均匀性有一定的波动。综合考虑衬垫与箱壁间空隙宽度对预冷时间和预冷均匀性的影响,本文得到的最佳空隙宽度增量为7.5 mm,与现有设计方案(ΔWgap=0 mm)相比,采用最佳方案能够使得预冷时间缩短16%,预冷结束时的均匀性提高20.11%。
| [1] |
王文生, 杨少桧, 闫师杰. 我国果蔬冷链发展现状与节能降耗主要途径[J]. 保鲜与加工, 2016, 16(2): 1-5. |
| [2] |
Wu W, Defraeye T. Identifying heterogeneities in cooling and quality evolution for a pallet of packed fresh fruit by using virtual cold chains[J]. Applied Thermal Engineering, 2018, 133: 407-417. Doi:10.1016/j.applthermaleng.2017.11.049 |
| [3] |
Vigneault C, Goyette B. Design of plastic container opening to optimize forced-air precooling of fruits and vegetables[J]. Applied Engineering in Agriculture, 2002, 18(1): 73-76. |
| [4] |
Delele M A, Verboven P, Ho Q T, et al. Advances in mathematical modelling of postharvest refrigeration processes[J]. Stewart Postharvest Review, 2010, 2(1): 1-8. |
| [5] |
Delele M A, Ngcobo M E K, Getahun S T, et al. Studying airflow and heat transfer characteristics of a horticultural produce packaging system using a 3-D CFD model. Part Ⅰ: Model development and validation[J]. Postharvest Biology and Technology, 2013, 86: 536-545. Doi:10.1016/j.postharvbio.2013.08.014 |
| [6] |
Delele M A, Ngcobo M E K, Getahun S T, et al. Studying airflow and heat transfer characteristics of a horticultural produce packaging system using a 3-D CFD model. Part Ⅱ: Effect of package design[J]. Postharvest Biology and Technology, 2013, 86: 546-555. Doi:10.1016/j.postharvbio.2013.08.015 |
| [7] |
Han J W, Qian J P, Zhao C J, et al. Mathematical modelling of cooling efficiency of ventilated packaging: integral performance evaluation[J]. International Journal of Heat and Mass Transfer, 2017, 111: 386-397. Doi:10.1016/j.ijheatmasstransfer.2017.04.015 |
| [8] |
Han J W, Zhao C J, Yang X T, et al. Computational modeling of airflow and heat transfer in a vented box during cooling: optimal package design[J]. Applied Thermal Engineering, 2015, 91: 883-893. Doi:10.1016/j.applthermaleng.2015.08.060 |
| [9] |
Zhao C J, Han J W, Yang X T, et al. A review of computational fluid dynamics for forced-air cooling process[J]. Applied Energy, 2016, 168: 314-331. Doi:10.1016/j.apenergy.2016.01.101 |
| [10] |
Dehghannya J, Ngadi M, Vigneault C. Mathematical modeling procedures for airflow, heat and mass transfer during forced convection cooling of produce: a review[J]. Food Engineering Reviews, 2010, 2(4): 227-243. Doi:10.1007/s12393-010-9027-z |
| [11] |
Verboven P, Tijskens E, Ramon H, et al. Virtual filing and airflow simulation of boxes with horticultural products[J]. Acta Horticulturae, 2005, 687: 47-54. |
| [12] |
韩佳伟. 多层级苹果预冷过程模拟及预冷控制决策优化[D]. 北京: 北京工业大学, 2018.
|
| [13] |
de Castro L R, Vigneault C, Cortez L A B. Cooling performance of horticultural produce in containers with peripheral openings[J]. Postharvest Biology and Technology, 2005, 38(3): 254-261. Doi:10.1016/j.postharvbio.2005.07.004 |
| [14] |
Delele M A, Tijskens E, Atalay Y T, et al. Combined discrete element and CFD modelling of airflow through random stacking of horticultural products in vented boxes[J]. Journal of food engineering, 2008, 89(1): 33-41. Doi:10.1016/j.jfoodeng.2008.03.026 |
| [15] |
Defraeye T, Lambrecht R, Delele M A, et al. Forced-convective cooling of citrus fruit: cooling conditions and energy consumption in relation to package design[J]. Journal of food engineering, 2014, 121: 118-127. Doi:10.1016/j.jfoodeng.2013.08.021 |
| [16] |
Wang D, Lai Y, Zhao H, et al. Numerical and experimental investigation on forced-air cooling of commercial packaged strawberries[J]. International Journal of Food Engineering, 2019, 15(7): 831-838. |
| [17] |
Pathare P B, Opara U L, Vigneault C, et al. Design of packaging vents for cooling fresh horticultural produce[J]. Food and Bioprocess Technology, 2012, 5(6): 2031-2045. Doi:10.1007/s11947-012-0883-9 |
| [18] |
Dehghannya J, Ngadi M, Vigneault C. Transport phenomena modelling during produce cooling for optimal package design: thermal sensitivity analysis[J]. Biosystems Engineering, 2012, 111(3): 315-324. Doi:10.1016/j.biosystemseng.2012.01.001 |
| [19] |
Berry T M, Defraeye T, Nicolaï B M, et al. Multiparameter analysis of cooling efficiency of ventilated fruit cartons using CFD: impact of vent hole design and internal packaging[J]. Food and Bioprocess Technology, 2016, 9(9): 1481-1493. Doi:10.1007/s11947-016-1733-y |
| [20] |
陈秀勤, 卢立新, 王军. 包装箱内层装果品差压预冷温度场的数值模拟与验证[J]. 农业工程学报, 2014, 30(12): 249-257. Doi:10.3969/j.issn.1002-6819.2014.12.031 |
| [21] |
Opara L U, Zou Q. Sensitivity analysis of a CFD modelling system for airflow and heat transfer of fresh food packaging: inlet airflow velocity and inside-package configurations[J]. International Journal of Food Engineering, 2007, 3(5): 1556-1571. |
| [22] |
Gruyters W, Defraeye T, Verboven P, et al. Reusable boxes for a beneficial apple cold chain: a precooling analysis[J]. International Journal of Refrigeration, 2019, 106: 338-349. Doi:10.1016/j.ijrefrig.2019.07.003 |
| [23] |
Tanner D J, Cleland A C, Robertson T R. A generalised mathematical modelling methodology for design of horticultural food packages exposed to refrigerated conditions: Part 3, mass transfer modelling and testing[J]. International Journal of Refrigeration, 2002, 25(1): 54-65. Doi:10.1016/S0140-7007(01)00017-2 |
| [24] |
O'Sullivan J, Ferrua M J, Love R, et al. Modelling the forced-air cooling mechanisms and performance of polylined horticultural produce[J]. Postharvest Biology and Technology, 2016, 120: 23-35. Doi:10.1016/j.postharvbio.2016.05.008 |
| [25] |
Berry T M, Fadiji T S, Defraeye T, et al. The role of horticultural carton vent hole design on cooling efficiency and compression strength: a multi-parameter approach[J]. Postharvest Biology and Technology, 2017, 124: 62-74. Doi:10.1016/j.postharvbio.2016.10.005 |
| [26] |
王达, 贾斌广, 杨相政, 等. 苹果双向交替送风压差预冷的数值模拟[J]. 食品科技, 2019, 44(2): 40-45. |
 2021, Vol. 38
2021, Vol. 38 


