汞是一种常见的工业原料和产物,具有剧毒性且能在生态系统中进行生物积累,对环境和人体健康有着极大的破坏力[1-3]。为限制汞在大气中的排放,2013年联合国通过了一项具有全球法律约束力的《水俣公约》[4]。在《水俣公约》中提到有色金属冶炼和火力发电厂是最重要的汞排放来源。而中国作为燃煤大国,是全球大气汞排放量最多的国家之一,约占全球大气汞排放总量的33%左右,并且每年以4.8%的速度递增[5],因此中国在新型汞污染排放控制技术的研究上面临十分严峻的挑战。
目前,活性炭喷射除汞技术(powdered sorbent injection, PSI)是公认最有潜力的燃煤脱汞技术之一[6]。PSI技术的原理是在除尘设备(静电除尘器或布袋除尘器)上游的烟道喷入粉状吸附剂,通常是粉状活性炭颗粒(pulverized activated carbon, PAC)。在流动过程中,吸附剂颗粒吸附烟气中的汞,将气态单质汞转化为氧化态汞和颗粒状汞,最终通过颗粒去除装置将这些活性炭与汞协同脱除[7]。
静电除尘器(electrostatic precipitator, ESP)是目前燃煤电厂运用最多的高效除尘设备之一,其基本原理是通过电极高压放电使空气电离,让粉尘颗粒荷电从而在电场力作用下附着到集尘板上[8]。由于静电除尘本身是一个较为复杂的多场耦合的气固两相流问题,特别是考虑到颗粒迁移和电动力(electro hydrodynamic, EHD)效应的影响,研究ESP中汞和吸附剂颗粒同时去除的机理是一项挑战。此前有许多学者利用实验或数值模拟手段研究活性炭喷射脱汞的机理和操作参数的影响,例如周强等[9]利用模拟烟气管道喷射脱汞实验平台进行活性炭喷射除汞实验,重点研究活性炭尺寸、烟气温度、汞浓度等因素对汞脱除的影响。任建莉等[10]建立活性炭吸附汞的吸附动力学数学模型,并通过对模拟烟气吸附实验数据进行拟合得到相应的吸附参数,能有效预测活性炭脱汞的除汞效率。Clack[11]利用数值模拟手段分析在静电力作用条件下活性炭颗粒的迁移和汞吸附机理,但该模型对于非均匀电场及颗粒的微观运动特性无能为力。总的来说,目前人们对于ESP中较为复杂的活性炭与汞协同脱除的机理与影响因素仍缺乏足够清晰的认识,也少有相关研究报道。针对此现状本文建立典型ESP中的耦合电场、传质及颗粒运动的多场数值模型,并分析在ESP内两种不同的汞吸附机制作用下,活性炭颗粒粒径、离子风效应对于汞吸附效率的影响,这对于燃煤电厂选择运行参数,达到最佳脱汞效果,降低脱汞成本有着一定的借鉴意义。
1 数值建模方法本文建立了ESP内部包含流场、电晕电场、离子密度场、颗粒荷电模型以及汞吸附的多场耦合数理模型,由商业软件ANSYS FLUENT实现对网格的处理及运算,通过其二次开发功能用户自定义函数(user defined function, UDF)和用户自定义标量(user defined scalar, UDS)建立统一的对流扩散方程,从而计算得到静电除尘内电场及汞浓度分布。对于活性炭颗粒的运动,采用拉格朗日方法对颗粒的轨迹进行追踪(考虑库仑力及曳力),颗粒的荷电速率利用Lawless和Sparks[12]提出的综合荷电方程来计算。
1.1 气相控制方程在工业ESP中,由于离子风效应的干扰,绝大多数ESP内的流场处于紊流状态,只有少数双区ESP能达到接近层流状态[13]。因此,本文采用雷诺时均湍流模型(Reynolds average Navier-Stokes, RANS)对ESP内的流场进行数值模拟。对于稳态湍流,控制方程如下:
质量守恒方程
| $ \frac{\partial }{{\partial {x_i}}}(\rho {u_i}) = 0, $ | (1) |
动量守恒方程
| $ \begin{array}{l} \frac{\partial}{\partial x_{j}}\left[\rho u_{i} u_{j}-\left(\mu+\mu_{\mathrm{t}}\right) \frac{\partial u_{i}}{\partial x_{j}}\right]=-\frac{\partial p}{\partial x_{i}}+ \\ f_{\mathrm{D} i}+\left(\rho_{\mathrm{ion}}+\rho_{\mathrm{pc}}\right) E_{i}, \end{array} $ | (2) |
其中: ui是流体速度在xi方向的分量; μt是湍流黏性系数; fDi是颗粒对流体造成的的曳力; ρion, ρpc分别代表离子电荷密度和颗粒电荷密度,二者之和即为空间电荷密度; Ei是电场强度分量; (ρion+ρpc)Ei项代表电场对流场产生的离子风效应。
1.2 电场控制方程在干式ESP中,电晕产生的电场可用泊松方程和电流连续性方程表示:
泊松方程
| $ \frac{\partial^{2} \varphi}{\partial x_{i}^{2}}=-\frac{\rho_{\mathrm{ion}}+\rho_{\mathrm{pc}}}{\varepsilon_{0} \varepsilon_{\mathrm{r}}}, $ | (3) |
电流连续性方程
| $ \frac{\partial}{\partial x_{i}}\left[\rho_{\text {ion }}\left(k_{\text {ion }} E_{i}+u_{i}\right)-D_{\mathrm{e}} \frac{\partial \rho_{\text {ion }}}{\partial x_{i}}\right]=0 , $ | (4) |
| $ E_{i}=-\frac{\partial \varphi}{\partial x_{i}}. $ | (5) |
泊松方程和电流连续性方程可以用如下统一的广义扩散对流输运方程进行表述:
| $ \frac{\partial}{\partial x_{i}}\left(F_{i} \varPhi-\varGamma_{\varPhi} \frac{\partial \varPhi}{\partial x_{i}}\right)=S_{\varPhi}. $ | (6) |
其中:φ为电势;ε0为真空介电常数,εr为烟气的相对介电常数,取值分别为8.854×10-12 F/m以及4.0; kion为离子迁移率,取3.0×10-4 m2/(s·V); Ei为场强在xi方向上的分量; De为离子的有效扩散系数,根据工况温度取1.02×10-5 m2/s。具体对应项如表 1所示。
|
|
表 1 电势、离子电荷密度及汞浓度的标量输运方程对应项 Table 1 Terms of the scalar transport equations of electric potential, charge density, and mercury concentration |
表 1中:Φ为所研究的标量(电势及离子荷电密度);Fi为对流通量;ΓΦ为扩散系数;SΦ为源项。电势、离子电荷密度场及汞浓度场通过Fluent提供的UDS功能迭代计算。
1.3 颗粒荷电模型颗粒在电晕场中运动时会带上一定的电量,荷电机制主要分为电场荷电与扩散荷电。粒子的荷电量决定了颗粒所受静电力的大小从而影响到颗粒的运动以及对汞的吸附过程。Long和Yao[14]指出,Lawless[12]提出的综合荷电率模型能够较为准确地计算颗粒在运动过程中的总荷电量:
| $ \frac{{{\rm{d}}{q_{\rm{p}}}}}{{{\rm{d}}t}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{q_{\rm{s}}}}}{\tau }{{\left( {1 - \frac{q}{{{q_{\rm{s}}}}}} \right)}^2} + \frac{{2{\rm{ \mathsf{ π} }}\alpha \rho {k_{{\rm{ion}}}}{k_{\rm{B}}}{d_{\rm{p}}}}}{e},}&{q < {q_{\rm{s}}},}\\ {\frac{\alpha }{{4\tau }}\left( {q - {q_{\rm{s}}}} \right)\exp \left( {\frac{{e\left( {{q_{\rm{s}}} - q} \right)}}{{2{\rm{ \mathsf{ π} }}{\varepsilon _0}{k_{{\rm{ion}}}}{k_{\rm{B}}}T{d_{\rm{p}}}}}} \right),}&{q > {q_{\rm{s}}},} \end{array}} \right. $ | (7) |
| $ \alpha=\left\{\begin{array}{ll} 1, & e_{\text {norm }}<0.525, \\ \frac{1}{\left(e_{\text {norm }}+0.457\right)^{0.575}}, & e_{\text {norm }}>0.525, \end{array}\right. $ | (8) |
| $ {{e_{{\rm{norm}}}} = \frac{{e{d_{\rm{p}}}}}{{2{k_{\rm{B}}}T}}E,} $ | (9) |
| $ {\tau = \frac{{4{\varepsilon _0}}}{{{\rho _{{\rm{ion}}}}{k_{{\rm{ion}}}}}},} $ | (10) |
| $ {{q_{\rm{s}}} = 3\frac{{{\varepsilon _{\rm{r}}}}}{{{\varepsilon _{\rm{r}}} + 2}}{\rm{ \mathsf{ π} }}{\varepsilon _0}d_{\rm{p}}^2E,} $ | (11) |
其中: qs是颗粒的饱和荷电量, ε0为真空介电常数, εr是烟气的相对介电常数, τ是颗粒荷电的时间常数(颗粒荷电量为饱和荷电量一半时所花费的时间), kB为玻尔兹曼常数而e为单位电子的电量。
1.4 颗粒受力模型在拉格朗日坐标系中,采用DPM方法对气相中悬浮粒子进行跟踪。在典型的电除尘器质量加载速率下,气固两相流非常稀薄,颗粒间的相互作用可以忽略不计。Luo等[15]指出,流体拖曳力、Saffman升力、重力和库仑力是经典静电除尘器中颗粒所受的主要体积力。在目前的分析中,与流体阻力和库仑力相比,Saffman升力和重力被证明是微不足道的[16]。因此,粒子运动方程可以描述为
| $ \frac{\mathrm{d} \boldsymbol{u}_{\mathrm{p}}}{\mathrm{d} t}=\frac{18 \mu}{d_{\mathrm{p}}^{2} \rho_{\mathrm{p}} C_{\mathrm{C}}}\left(\boldsymbol{u}_{\mathrm{g}}-\boldsymbol{u}_{\mathrm{p}}\right)+\frac{q_{\mathrm{p}} \boldsymbol{E}}{m_{\mathrm{p}}}, $ | (12) |
其中
| $ C_{\mathrm{c}}=1+\frac{2 \lambda}{d_{\mathrm{p}}}\left(1.257+0.4 e^{-1.1 d_{\mathrm{p}} / 2 \lambda}\right), $ | (13) |
mp为颗粒质量, ug为烟气流速, up为颗粒运动速度, Cc为康宁汉姆修正系数, λ是空气的平均自由程。式(12)右边的项分别表示流体曳力和库仑力。大约有1 020个粒子从ESP的入口喷射出来,采用DPM方法对气相中悬浮粒子进行跟踪。
1.5 活性炭汞吸附模型ESP中喷入的活性炭颗粒对于气相单质汞的吸附主要基于2种机制:悬浮颗粒吸附与近壁面吸附[11]。有学者分别对2种机制对于汞吸附的影响进行过研究,但2种机制的综合作用效果和机理尚不明了。在实际工业运用中,由于干式ESP的集尘级上覆盖着由活性炭吸附剂与粉尘混合组成的粉尘层,因此在ESP中,两种吸附机制是同时作用的。
无论是哪种吸附机制,都包含着复杂的物理吸附与化学吸附过程。活性炭对汞的吸附过程包括3个主要步骤:膜传质、颗粒内扩散以及汞在活性点位的吸附[17]。通常后两者的发生速率都远快于膜传质过程。基于此,建立吸附模型过程中做如下假设:1)膜传质过程即烟气中气相汞分子向活性炭颗粒表面传递的过程是决定整体吸附速率的步骤;2)忽略颗粒内扩散及活性点位吸附所带来的传质阻力,即将颗粒外表面的汞浓度视为零;3)活性炭颗粒在ESP中较短的停留时间里远远达不到吸附饱和状态。
从而可以利用菲克定律计算膜传质的速率:
| $ N_{\mathrm{A}}=M \frac{\mathrm{d} q_{\mathrm{s}}}{\mathrm{d} t}=k_{\mathrm{g}} a\left(C_{\mathrm{g}}-C_{\mathrm{i}}\right), $ | (14) |
其中: NA为传质速度,kg/(m3·s); kg为膜传质系数,m/s; a为活性炭颗粒的比表面积,m2/m3; Cg为颗粒外部烟气中气相汞的平均浓度,Ci为活性炭表面的汞浓度(假设为零),kg/m3。
膜传质系数kg可由舍伍德数Sh确定:
| $ k_{\mathrm{g}}=\frac{S h D_{\mathrm{M}}}{d_{\mathrm{p}}}, $ | (15) |
其中: DM为气态汞在空气中的扩散系数; m2/s;dp为活性炭粒径,m。而舍伍德数Sh则是谢密特数Sc与颗粒雷诺数Rep的函数:
| $ S h=2.0+0.6 S c^{\frac{1}{3}} {R e_{\mathrm{p}}}^{\frac{1}{2}}. $ | (16) |
通过以上关系式可以得到单个活性炭颗粒吸附气相单质汞的速率,而利用拉格朗日方法追踪活性炭粒子在ESP中的轨迹,可以计算出每一个控制体积中的颗粒数量密度,从而得到每一个控制体积(网格)中单位时间内被吸附的汞单质质量
| $ \dot{M}_{\mathrm{Hg}}=K_{\mathrm{g}} a\left(C_{\mathrm{g}}-C^{*}\right)=N D_{\mathrm{P}} K_{\mathrm{g}} a\left(C_{\mathrm{g}}-0\right), $ | (17) |
其中:NDP是颗粒数量密度,个/m3。而对于近壁面的吸附问题,假设整个收尘板都被活性炭颗粒均匀覆盖,那么在不考虑粉尘层堆积的情况下,可以粗略地认为整个收尘极板表面的单质汞浓度为零,被壁面吸附的汞单质的质量通量通过式(6)的对流扩散方程来计算。在实际中,吸附剂只占粉尘层的一小部分,但考虑到烟尘对于汞单质也有一定的吸附作用,且有研究[11]证明采用此假设对于研究近壁面汞单质的相对浓度变化没有太大影响,因此该边界条件不会影响到对于ESP内汞吸附机制的研究。
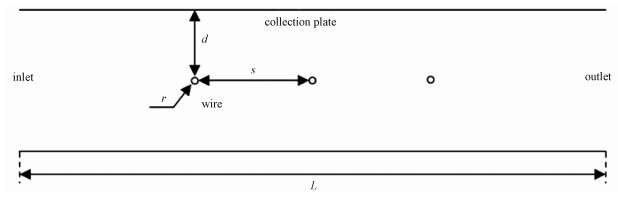
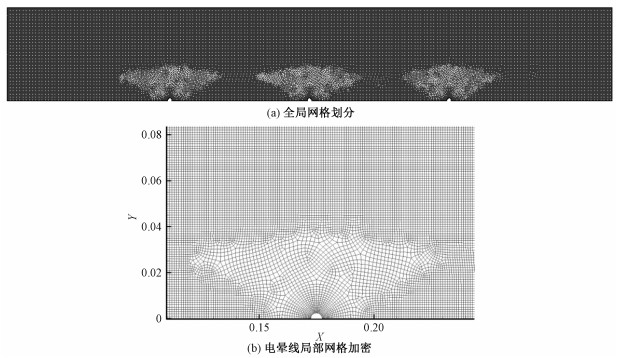
2 物理模型及边界条件 2.1 几何模型建立在本文中,为简化问题、减少网格量,采用的是二维的线板式ESP物理模型,几何结构如图 1所示。集尘极的总长度为0.65 m,3根直径为5 mm的圆形电晕极以0.15 m的间距等距排列,电晕极与集尘极的距离为0.1 m。为了在不影响结果的同时降低计算量,以ESP水平中心线为轴对称地选取模型的1/2作为计算域并划分网格。在整个计算域中生成质量较高的结构化网格,并且由于电晕极周围电场强度梯度较大,对电晕极附近的网格进行加密。此外,考虑到计算结果对网格的独立性要求,对网格无关性进行了检验。用33 098、62 879、91 645和209 811共4种不同网格数量的计算域计算同一工况(393 K, 进口流速1 m/s, 颗粒直径5 μm)下的活性炭除汞效率,分别为85.9%、89.8%、89.5%和89.3%。考虑到当网格量大于62 879时颗粒收集效率已无显著变化,为了提升计算效率,我们选择的计算域划分网格数量为62 879个,如图 2所示。
|
Download:
|
| 图 1 ESP几何结构 Fig. 1 ESP geometric construction | |
|
Download:
|
| 图 2 模型网格划分结构 Fig. 2 The grid scheme of the physical model | |
在数值计算中运用的边界条件见表 2。除了流场和离散相模型外,数值模型中的电势、离子电荷密度和汞浓度场3个标量需要给定边界条件。电晕极表面的电势为运行电压,值得注意的是电晕极表面的离子电荷密度则需要特别的处理,先用Peek定律计算得到电晕极的表面场强,随后迭代求解强耦合的离子电荷密度和表面场强,直到得到的表面场强值与Peek定律计算得到的场强值相等(一定残差范围内),则认为收敛,取最终的离子电荷密度作为电晕极边界值。收尘板(接地极)处的电势为0,离子电荷密度通量为0,单质汞浓度也为0。入口和出口的电势、离子电荷密度及单质汞浓度的通量均为0。
|
|
表 2 边界条件 Table 2 Boundary conditions |
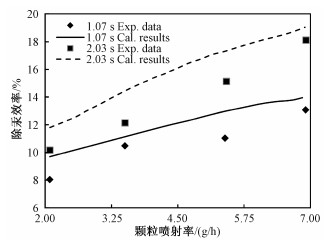
本文建立ESP内活性炭汞吸附的数值模型,由于在工业尺寸ESP内进行的活性炭喷射脱汞测试较少,且相关测试报告也都缺乏所测试ESP的几何参数和运行条件,因此为了验证本文所建立汞吸附模型的准确性,将模拟结果与周强等[9]的烟道活性炭脱汞实验结果进行对比。虽然该实验是在烟道内而不是ESP内进行的,但活性炭脱汞机理相同。计算区域长2 m, 内径为16 mm,模拟工况为: 烟气温度120 ℃,活性炭粒径为31.5 μm,喷射量2.2~6.9 g/h。对两种停留时间下的除汞效率进行对比,如图 3所示。
|
Download:
|
| 图 3 模型除汞效率与实验结果对比 Fig. 3 Comparison of mercury removal efficiencies between modeling results and experimental data | |
不难发现,模拟结果与实验结果在趋势上吻合较好,除汞效率随着停留时间和活性炭喷射量的提高而提高,但模拟得到的除汞效率相对实验值都偏高,最大相对误差值约为12.1%,这也是符合预期的。由于在建立除汞模型时便忽略了活性炭颗粒内部的传质阻力,假设颗粒外表面汞浓度始终为零,而在实际中活性炭颗粒内部的扩散和吸附速率都是有限的,尤其是未经过化学改性处理的活性炭。因此本模型将会高估颗粒吸收的气态单质汞质量,在相同工况下得到的除汞效率大于实际值。即使如此,本模型还是能够较好地表现出ESP内不同因素对于除汞效率的影响,对于研究活性炭除汞的机制有一定的帮助。若在未来的研究工作中,加入颗粒内部的扩散阻力和化学吸附的影响,对于提高汞吸附模型的准确度十分有帮助。
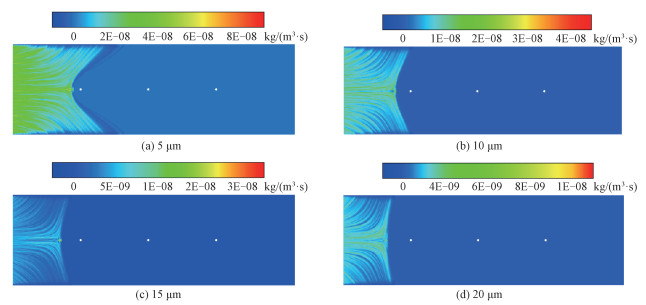
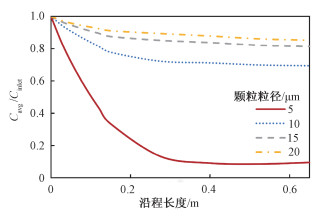
3.2 活性炭粒径对汞吸附的影响在典型的ESP运行工况(即烟气温度120 ℃,初始汞浓度为1×10-8 kg/m3,烟气入口速度为1.0 m/s, 活性炭质量流量为2.2×10-6 kg/s, 电极运行电压为70 kV)下, 模拟结果表明,活性炭粒径对汞吸附有着重要的影响,如图 4、图 5所示。值得注意的是,由于粒径大小对于近壁面汞吸附的影响微乎其微,在这里只讨论粒径对于悬浮颗粒吸附的影响。随着粒径从5 μm增加到20 μm,从图 4可以看出,活性炭颗粒吸附汞的能力在降低,且所喷入活性炭颗粒在ESP内的吸附范围也在减小。因此活性炭颗粒粒径的增加将会造成ESP内汞脱除效率的降低,图 5所显示的ESP内汞单质平均浓度的变化证实了这一点,当活性炭粒径为5 μm时,ESP脱汞效率可以达到89.6%,而当粒径为20 μm时,脱汞效率急剧下降到12.3%。当减小活性炭粒径时,活性炭颗粒的外比表面积增大,因此在同样的活性炭质量流量下颗粒的表面积更大,总的传质速率更大。此外,由式(7)、式(8)及式(10)可知,当颗粒粒径减小时,颗粒雷诺数和舍伍德数均增大,膜传质系数kg增加,从而使得颗粒吸附汞的效率显著提升。
|
Download:
|
| 图 4 活性炭颗粒粒径对汞吸附的影响 Fig. 4 Mercury adsorption per unit volume in a unit time for different particle sizes | |
|
Download:
|
| 图 5 活性炭颗粒粒径对汞吸附效率的影响 Fig. 5 Average mercury concentration along the downstream direction | |
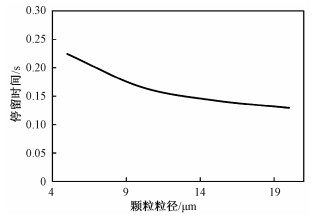
值得注意的是,颗粒粒径也对吸附剂在ESP内的停留时间有着较大影响,如图 6所示。当活性炭颗粒粒径减小时,颗粒在ESP内的停留时间也随之增加,这是由于小粒径颗粒受到的静电体积力较小从而其向极板方向的迁移速度较小,因此颗粒在ESP内停留时间增加,这意味着烟气汞分子与活性炭发生碰撞而吸附的概率增大,脱汞效率由此得到提高。因此在相同的碳汞比时,使用更小粒径的吸附剂显然会得到更高的脱汞效率。但大幅减少吸附剂颗粒尺寸,会增加吸附剂的生产成本,且ESP收集颗粒物的效率是随着粒径减小而下降的,当粒径小于2.5 μm时,除尘效率将低于95%,这将附加地产生许多微颗粒污染物,如PM2.5。因此在选择活性炭粒径时应当平衡好除汞效率与除尘效率,在保证除汞效率的同时不产生额外的颗粒污染物。
|
Download:
|
| 图 6 活性炭颗粒粒径对停留时间的影响 Fig. 6 Variation of residence time with different particle diameters | |
离子风(ionic wind),又称电晕风(corona wind)、电风(electric wind)或二次流(second flow)。之所以称为电晕风或离子风,是因为它是电晕放电产生的离子在电场中迁移引起的流动。离子风对于ESP内的能量、动量和能量交换有着重要的影响。离子风效应的强弱常用无量纲数NEHD来表示:
| $ N_{\mathrm{EHD}}=\frac{i}{b \rho u^{2}}=\frac{\rho_{\mathrm{ion}} E}{\rho u^{2} / d}=\frac{\text { 离子风 }}{\text { 惯性力 }}, $ | (18) |
式中:i是单位长度电晕极的电流密度,u是ESP入口处的气体平均速度。可以发现影响NEHD大小的主要参数是场强和主流速度的大小,因此通过改变这2个参数便能研究不同离子风强度对于汞吸附的影响。本文将分别从悬浮颗粒吸附与近壁面吸附两种机制来阐述离子风对汞吸附的影响。
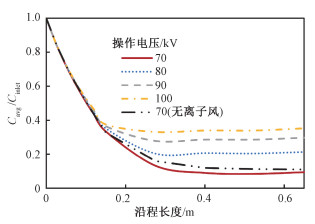
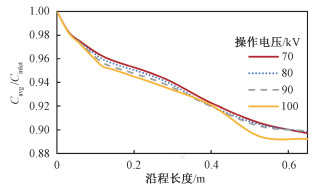
从图 7显示的结果来看,离子风效应对于悬浮活性炭颗粒的汞吸附有着重要影响。当运行电压为70 kV时,若不考虑离子风效应的影响,即去掉气相动量方程的离子风项(ρion+ρpc)Ei,可以看到悬浮活性炭颗粒吸附汞的效率相比有离子风的条件下降约2%。说明在ESP内离子风的存在能够提升活性炭汞吸附的效率,这是由于离子风能在ESP内形成漩涡,漩涡将使湍流强度增加,这对于加强颗粒与气相之间的传质作用是有利的。而当增加ESP的运行电压使离子风强度增大时,却发现除汞效率反而降低了,不难得出这是因为电压的增大使得颗粒受到的电场力增加,使得活性炭颗粒很快便被收集到集尘板上,停留时间变短,而湍流强度的增加对传质效率的增加远小于停留时间减小对除汞效率的削弱,因此总的活性炭颗粒除汞效率随着电场强度的增加而减小。这说明想通过提升电场强度来增加脱汞效率是不可行的。
|
Download:
|
| 图 7 离子风对颗粒汞吸附效率的影响 Fig. 7 Average mercury concentration along the downstream direction under different EHD conditions | |
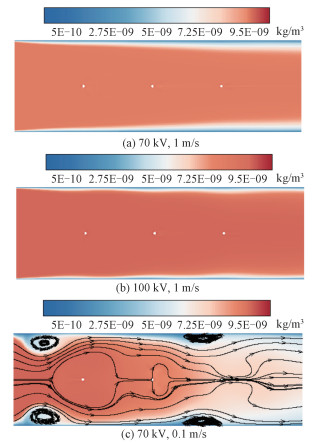
电场强度对于近壁面汞吸附的作用则有所不同。图 8直观地显示了仅考虑壁面吸附的ESP内单质汞浓度分布图。不难发现沿着极板方向形成了汞吸附传质的边界层,且厚度随流动方向而增长。比较2种电场强度下气相汞浓度的分布可以发现,当电场强度增加时,离子风对于边界层的扰动效应增强,使得局部的传质边界层厚度减小,垂直壁面的浓度梯度增大,由菲克定律可知传递向壁面的汞单质质量通量随之增大。如图 9所示,当运行电压由70 kV增大到100 kV时,近壁面除汞的效率由7.77%增加到9.92%,这证明了离子风形成的漩涡对于加强集尘板上收集的活性炭颗粒层吸收单质汞有一定的增强作用。而当烟气入口速度减小时,无量纲数NEHD增大,离子风效应加强,由图 8(c)可知,离子风形成的主要漩涡区对应着汞吸附量较大的区域,整体的壁面汞吸附效率提高到40.4%。因此通过适当减小烟气入口速度能够提高收尘极壁面对汞的吸附量,若考虑悬浮颗粒的吸附,可以预料到的是,随着活性炭颗粒入口速度的减小,在ESP内的停留时间增加,因此悬浮颗粒脱汞效率也会增大。从而不难得出结论,适当的减小入口烟气速度能够提高ESP中整体的脱汞效率。
|
Download:
|
| 图 8 离子风对近壁面汞吸附的影响 Fig. 8 EHD effects on wall-bounded mercury capture | |
|
Download:
|
| 图 9 离子风对近壁面汞吸附的影响 Fig. 9 EHD effects on wall-bounded mercury capture efficiencies | |
从表 3显示的结果可以看出,当悬浮颗粒脱汞与近壁面脱汞两种吸附机制共同作用时,效果要比两种吸附机制单独作用的叠加效果弱,即两种机制共同作用的吸附量要大大小于悬浮颗粒脱汞量与壁面脱汞量之和。这是由于悬浮颗粒吸附效率远大于壁面吸附,因此在活性炭颗粒甫一进入ESP,大部分的气相汞单质就被活性炭颗粒所吸附,整体的汞浓度降低,相对于壁面的汞浓度梯度减小,由菲克定律不难得到烟气汞相对于壁面的传质通量将减小,汞吸附量下降。因此可以得出结论,在ESP内两种脱汞机制共同作用时,壁面吸附的作用较小,特别是在壁面零浓度条件将高估壁面吸附量的前提下,这与Clack[18]的模拟结果相同。
|
|
表 3 两种吸附机制脱汞效率 Table 3 Removal efficiencies of two mercury adsorption mechanisms |
1) 建立的活性炭喷射脱汞预测模型,能较好地预测活性炭的脱汞率,模型预测的脱汞效率与实验结果具有相同的变化趋势, 最大相对误差约为12.1%; 该模型可用于预测ESP内烟气喷射活性炭脱汞过程.
2) 减小活性炭粒径,不仅增大活性炭的单位外表面积,而且增大烟气汞向活性炭表面传递的膜传质速率和在ESP内的停留时间,提高了喷射脱汞的效率。当活性炭粒径为5 μm时,ESP脱汞效率可以达到89.6%,而当粒径为20 μm时,脱汞效率急剧下降到12.3%。但过小的吸附剂颗粒尺寸,会增加吸附剂的生产成本,并产生额外的颗粒污染物如PM2.5。
3) 离子风能在ESP内形成漩涡,漩涡将使湍流强度增加,这对于加强颗粒与气相之间的传质作用是有利的,即离子风能够提高悬浮活性炭对汞的吸附作用,相较于无离子风条件下能使除汞效率提升2%。但若通过提升电压的方式来提高离子风强度反而会使除汞效率下降,这与颗粒在ESP内停留时间的缩短密切相关。
4) 离子风形成的漩涡同样能提高收尘极壁面对汞烟气的吸附速率,壁面吸附的效率最大可达到40.4%,但在烟气速度较大的工况下离子风的影响较小。在ESP内两种脱汞机制共同作用时,壁面吸附的作用较小,颗粒吸附作用占主导地位。
| [1] |
Hsi H C, Tsai C Y, Kuo T H, et al. Development of low-concentration mercury adsorbents from biohydrogen-generation agricultural residues using sulfur impregnation[J]. Bioresource Technology, 2011, 102(16): 7470-7477. Doi:10.1016/j.biortech.2011.05.036 |
| [2] |
杨振宇, 羌宁, 季学李. 美国燃煤电厂锅炉烟气中汞的研究进展[J]. 能源环境保护, 2003, 17(5): 3-7. Doi:10.3969/j.issn.1006-8759.2003.05.001 |
| [3] |
Pavlish J H, Sondreal E A, Mann M D, et al. Status review of mercury control options for coal-fired power plants[J]. Fuel Processing Technology, 2003, 82(2/3): 89-165. |
| [4] |
United Nations Environment Programme(UNEP). Minamata convention on mercury[R]. Geneva, Switzerland: UNEP, 2013.
|
| [5] |
Niksa S, Fujiwara N. Estimating Hg emissions from coal-fired power stations in China[J]. Fuel, 2009, 88(1): 214-217. Doi:10.1016/j.fuel.2008.07.017 |
| [6] |
Lee S H, Rhim Y J, Cho S P, et al. Carbon-based novel sorbent for removing gas-phase mercury[J]. Fuel, 2006, 85(2): 219-226. Doi:10.1016/j.fuel.2005.02.030 |
| [7] |
陶叶. 火电机组烟气脱汞工艺路线选择[J]. 电力建设, 2011, 32(4): 74-78. Doi:10.3969/j.issn.1000-7229.2011.04.018 |
| [8] |
While H J. Industrial electrostatic precipitation[M]. New York: Addison-Wesley, 1963.
|
| [9] |
周强, 段钰锋, 洪亚光, 等. 模拟烟气活性炭喷射脱汞实验研究[J]. 中国电机工程学报, 2013, 33(35): 36-43. |
| [10] |
任建莉, 周劲松, 骆仲泱, 等. 活性炭吸附烟气中气态汞的试验研究[J]. 中国电机工程学报, 2004, 24(2): 171-175. Doi:10.3321/j.issn:0258-8013.2004.02.033 |
| [11] |
Clack H L. Particle size distribution effects on gas-particle mass transfer within electrostatic precipitators[J]. Environmental Science and Technology, 2006, 40: 3929-3933. Doi:10.1021/es051649c |
| [12] |
Lawless P A, Sparks L E. Modeling particulate charging in ESPs[J]. IEEE Transactions on Industry Applications, 1988, 24: 922-927. Doi:10.1109/28.8999 |
| [13] |
Li Y, Zheng C H, Luo K, et al. CFD simulation of high-temperature effect on EHD characteristics in a wire-plate electrostatic precipitator[J]. Chinese Journal of Chemical Engineering, 2015, 23: 633-640. Doi:10.1016/j.cjche.2014.06.038 |
| [14] |
Long Z W, Yao Q. Numerical simulation of the flow and the collection mechanism inside a scale hybrid particulate collector[J]. Powder Technology, 2012, 215/216: 26-37. Doi:10.1016/j.powtec.2011.08.045 |
| [15] |
Luo K, Li Y, Zheng C H, et al. Numerical simulation of temperature effect on particles behavior via electrostatic precipitators[J]. Applied Thermal Engineering, 2015, 88: 127-139. Doi:10.1016/j.applthermaleng.2014.11.078 |
| [16] |
毕文剑, 李艳, 罗坤, 等. 温度对静电除尘器内颗粒受力影响的数值模拟[J]. 中国科学院大学学报, 2017, 34(2): 172-178. |
| [17] |
近藤精一, 石川达雄, 安部郁夫. 吸附科学[M]. 北京: 化学工业出版社, 2005: 104-107.
|
| [18] |
Clack H L. Mass transfer within electrostatic precipitators: in-flight adsorption of mercury by charged suspended particulates[J]. Environmental Science and Technology, 2006, 40: 3617-3622. Doi:10.1021/es050246+ |
 2021, Vol. 38
2021, Vol. 38 


