随着金融行业快速发展、大众消费观念极速改变，个人信贷产品不断丰富，以及个人信贷业务规模大幅提升，个人信用风险问题日益突出。个人信用风险是目前商业银行面临的风险中最为重要和复杂的，因此如何进行有效的个人信用风险管理来降低违约风险成为研究的核心问题。《巴塞尔新资本协议》指出有条件的银行要实施内部评级法，通过对历史数据构建模型测算客户的违约概率^[1]。违约概率作为影响信用风险的关键因素之一，准确地评估客户的违约概率是信用风险计量的基础^[2]。而在信用风险管理方面，信用评分模型发挥着重要的作用。

目前，基于机器学习的个人信用评分模型有：线性判别分析^[3]、Logistic回归^[4]、神经网络^[5]、支持向量机^[6]、遗传算法^[7]、聚类分析^[8]、最近邻模型^[9]、决策树^[10]和贝叶斯方法^[11]等。其中，Logistic回归在个人信用评分中应用最为广泛。Logistic模型具有计算简单、解释性强与预测精度较高的优点，并且在中国房贷信用风险评估中得到验证^[12]。然而，随着社会和经济的不断发展，影响个人信用风险的因素在不断增加，传统的Logistic回归不能有效地处理模型中自变量存在多重共线性的问题，且过多变量增加了模型的复杂度，进而降低了模型预测的精准度。因此，不断有学者在此基础上进行深入研究。针对Logistic回归存在的缺陷，Lee和Zhang^[13]通过对个人信用评分模型中样本的非均匀抽样进行优化，提高了Logistic回归模型的预测性能。Jongh等^[14]提出通过大样本数据消除Logistic回归中的变量多重共线性对个人信用评分中的影响。魏秋萍和张景肖^[15]基于偏最小二乘方法构建信用评分模型，史小康和何晓群^[16]基于有偏的Logistic回归方法进行个人信用评级模型的应用研究，这两种方法都能有效地缓解评分模型中自变量存在多重共线性的问题。然而，上述模型也存在一定的局限性，没有充分考虑样本数据本身存在的非均衡性和缺失性，也没有对研究变量进行必要的选择。Tibshirani^[17]提出Lasso方法能够同时实现变量选择与参数估计，可以将模型中部分自变量的系数压缩使之趋于零，从而达到变量选择的目的。张婷婷和景英川^[18]直接将改进的adaptive Lasso-Logistic回归模型引入个人信用评分，他们的方法相比Lasso-Logistic回归具有更好的解释性与更高的预测精准度。然而，当数据中有分类变量时，Lasso方法通常不能得到满意的结果，因为Lasso方法只能选择单个哑变量，而不是整个分类变量，Group-Lasso方法很好地解决了这个问题。张娟和张贝贝^[19]采用基于Group-Lasso方法的广义半参数可加模型进行信用评分模型的应用研究，虽然该模型考虑利用Group-Lasso方法进行变量选择，将哑变量作为组进行整体的选择，但是缺乏对样本数据进行必要的处理。

为解决上述问题，本文尝试采用ROSE(random over sampling examples) 方法处理类别不均衡的信用卡数据之后，再使用Group-Lasso方法在Logistic回归模型中进行变量选择，构建个人信用评分模型。

1 模型与方法 1.1 Group-Lasso方法介绍

在线性回归模型中，记连续型响应变量为$ \boldsymbol{Y}\in {{\mathbb{R}}^{n}}, n\times p $维设计矩阵为X，系数向量为$ \boldsymbol{\beta} ={{\left( {{\beta }_{1}}, {{\beta }_{2}}, \cdots , {{\beta }_{p}} \right)}^{\text{T}}}\in {{\mathbb{R}}^{\text{p}}} $。Lasso估计^[17]定义如下

$ {{\widehat{\boldsymbol{\beta} }}_{\lambda }}=\text{argmin}\left( \|\boldsymbol{Y}-\boldsymbol{X\beta} \|_{2}^{2}+\lambda \sum\nolimits_{j=1}^{p}{\left| {{\beta }_{j}} \right|} \right), $

(1)

其中$ \boldsymbol{u}\in {{\mathbb{R}}^{n}}, \left\| \boldsymbol{u} \right\|_{2}^{2}=\sum\nolimits_{i=1}^{n}{u_{i}^{2}} $。当惩罚参数λ取值较大时，$ {{\boldsymbol{\hat{\beta} }}_{\lambda }} $的一些分量取0，从而达到选择变量的目的。Lasso方法的L₁惩罚项也可以用于其他模型，比如Cox模型、Logistic回归等，做法是将上述估计中的残差平方和项换为相应的负对数似然函数。

在线性回归模型中，当自变量除连续型变量，还含有分类变量时，Lasso方法通常不能得到满意的结果。传统Lasso方法只能选择单个的哑变量，而不是整个分类变量，Group-Lasso方法^[20]在Lasso方法的基础上解决了这个问题。其估计定义如下

$ {{\widehat{\boldsymbol{\beta} }}_{\lambda }}=\text{argmin}\left( \left\| \boldsymbol{Y}-\boldsymbol{X\beta} \right\|_{2}^{2}+\lambda \sum\nolimits_{g=1}^{G}{{{\left\| {{\boldsymbol{\beta} }_{{{\mathfrak{T}}_{g}}}} \right\|}_{2}}} \right), $

(2)

其中$ {{\mathfrak{T}}_{g}} $是第g组变量的下标集，$ {{\boldsymbol{\beta} }_{{{\mathfrak{T}}_{g}}}} $是第g组变量的系数向量，(g=1, 2, …, G)。Group-Lasso方法的惩罚项可以看作是L₁惩罚和L₂惩罚的中间状态^[21]，Group-Lasso方法在组的水平上选择变量，即成组地选择变量。例如，考虑一个具有K个水平的分类变量，在线性模型建模过程中，该分类变量是被转化为K-1个0-1变量，就可以看作一个组。Group-Lasso方法可以对这K-1个哑变量同时选择，而Lasso方法只能选出这K-1个哑变量中的一部分，这是没有实际意义的。

1.2 Logistic回归模型中的Group-Lasso变量选择

假设有独立同分布的样本(x_i, y_i)，i=1, 2, …, n，其中$ {{\boldsymbol{x}}_{i}}\in {{\mathbb{R}}^{p}} $对应于G组自变量，二元响应变量y_i∈0, 1，自变量可以为连续型变量或分类变量。记df_g为第g个自变量的自由度(degrees of freedom)^[22]，即第g组自变量的个数，于是可记$ {{\boldsymbol{x}}_{i}}={{\left( \boldsymbol{x}_{i, 1}^{\text{T}}, \cdots , \boldsymbol{x}_{i, G}^{\text{T}} \right)}^{\text{T}}} $，每一组变量$ {{\boldsymbol{x}}_{i, g}}\in {{\mathbb{R}}^{\text{d}{{\text{f}}_{g}}}}, g=1, 2, \cdots G $。

线性logistic回归模型对条件概率p_β(x_i)=P_β(y=1|x_i) 建模：

$ \log \frac{{{p}_{\beta }}\left( {{\boldsymbol{x}}_{i}} \right)}{1-{{p}_{\beta }}\left( {{\boldsymbol{x}}_{i}} \right)}={{\eta }_{\beta }}\left( {{\boldsymbol{x}}_{i}} \right), $

(3)

其中，

$ {{\eta }_{\beta }}\left( {{\boldsymbol{x}}_{i}} \right)={{\boldsymbol{\beta} }_{0}}+\sum\nolimits_{g=1}^{G}{\boldsymbol{x}_{i, g}^{\text{T}}{{\boldsymbol{\beta} }_{g}}}, $

(4)

$ {{\boldsymbol{\beta} }_{0}}=\mathbb{R} $是截距项，$ \boldsymbol{\beta} ={{\mathbb{R}}^{\text{d}{{\text{f}}_{g}}}} $是第g组自变量的系数向量，$ \boldsymbol{\beta} ={{\left( {{\boldsymbol{\beta} }_{0}}, \boldsymbol{\beta} _{1}^{\text{T}}, \cdots , \boldsymbol{\beta} _{G}^{\text{T}} \right)}^{\text{T}}}\in {{\mathbb{R}}^{p+1}} $是所有自变量的系数向量。Logistic回归的Group-Lasso估计$ {{\hat{\boldsymbol{\beta} }}_{\lambda }} $可通过最小化如下凸函数得到：

$ {{S}_{\lambda }}({\beta} )=-l(\boldsymbol{\beta} )+\lambda \sum\nolimits_{g=1}^{G}{s\left( \text{d}{{\text{f}}_{g}} \right){{\left\| {{\boldsymbol{\beta} }_{g}} \right\|}_{2}}}, $

(5)

其中l(·) 是对数似然函数：

$ l(\boldsymbol{\beta} )=\sum\nolimits_{i = 1}^n {{y_i}{\eta _\beta }\left( {{\boldsymbol{x}_i}} \right)} -\log \left[ 1+\exp \left\{ {{\eta }_{\beta }}\left( {{\boldsymbol{x}}_{i}} \right) \right\} \right]. $

(6)

参数λ控制惩罚力度，函数s(·) 根据系数向量的维数重新调整惩罚力度，如无特别说明，采用$ s\left( \text{d}{{\text{f}}_{g}} \right)=\text{df}_{g}^{1/2} $^[23]，参数估计采用Block Coordinate Descent算法^[23]。

1.3 ROSE(random over sampling examples)

在实际的二分类问题中，有许多情形是其中有一类样本非常少，而且通常是我们比较感兴趣的那一类。然而大部分模型更关注大类而忽视了小类的影响，这类类别不均衡问题会严重影响机器学习算法的拟合和预测效果^[24]。为处理上述问题，一般采取的方法是直接调整原始数据集的样本量，使得不同类别的数据样本之间达到均衡状态。基于这种直接产生新的数据样本来解决非均衡问题的主要方法有两种：一是基于数据层面，二是基于算法层面。

基于数据层面的方法主要是随机欠抽样法和随机过抽样法。1)随机欠抽样法是直接减少大类样本的样本量使得两类样本均衡，但采用这种方法会使得大类损失不少重要信息，导致结果不准确。2)随机过抽样法是增加小类样本的样本量使得两类样本均衡，但采用这种方法会重复增加小类的样本数据，增大计算负担，还有可能导致过拟合。基于算法层面的方法主要也有两种：一是代价敏感学习法，二是人造样本数据合成法。1)代价敏感学习法不直接生成均衡数据集，而是通过调节错分代价的方式，生成代价矩阵处理非均衡问题。该方法在非均衡数据的处理中具有较大的局限性，响应变量的不均匀分布使得算法精度下降，对于小类的预测精度会很低。而在非均衡的数据中，任一算法都没法从样本量少的类中获取足够的信息进行精确预测^[25]。2)人造样本数据合成法利用人造样本数据而不是重复原始样本数据处理非均衡问题，解决了生成样本重叠的问题。相对于随机欠抽样法或随机过抽样法而言，该方法没有重复利用样本数据，也没有减少样本信息。

在某些场合下，人造样本数据合成法相对于其他处理非均衡的方法而言具有一定的优势，其中最为有效和常用的是SMOTE(synthetic minority over-sampling technique)算法和ROSE算法。SMOTE算法是生成与小类观测相似的新数据，具体地说是在样本点和它近邻点的连线上随机投点作为生成的人造样本^[26]；ROSE算法则是基于各类别对应的自变量的条件核密度估计，产生类别均衡的人造样本^[27]。本文运用2种方法对数据进行非均衡处理之后，发现通过ROSE算法进行处理后的实证结果更加有效。所以，本文最终采用ROSE算法^[28]对数据进行非均衡处理。

考虑训练集T_n={(x_i, y_i), i=1, 2, …, n}，这里y_i∈{y₀, y₁} 是类别标签，x_i是某个总体$ \boldsymbol{x}\in {{\mathbb{R}}^{d}} $的一次实现(来自总体x的一个样本)，总体的概率密度f(x) 未知。n_j < n表示类别y_j的个数，ROSE算法通过以下步骤产生一个新的人造样本：

1) 以概率1/2选择y=Y_j, j=1, 2，

2) 以概率p_i=1/n_j在训练集T_n中选择样本(x_i, y_i) 使得y_i=y，

3) 从K_Hj(·, x_i) 中采样，其中K_Hj是一个概率分布，中心在x_i，H_j是刻度参数矩阵。

先从训练集中选择一个样本，然后在这个样本的邻域中产生一个新的样本，这个邻域的宽度由H_j决定。通常，K_Hj是一个单峰和对称的概率分布。在给定类别标签Y_j时，产生新的样本等价于由f(x|Y_j) 的核密度估计来采样，其中核函数为K_Hj。核函数K和“窗宽” H_j的选择是纯粹的核密度估计问题。给定标签时，条件密度如下

$ \begin{align} & \hat{f}\left( \boldsymbol{x}|y={{Y}_{j}} \right)=\sum\nolimits_{i=1}^{{{n}_{j}}}{{{p}_{i}}\text{Pr}\left( \boldsymbol{x}|{{\boldsymbol{x}}_{i}} \right)} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\sum\nolimits_{i=1}^{{{n}_{j}}}{\frac{1}{{{n}_{j}}}\text{Pr}\left( \boldsymbol{x}|{{\boldsymbol{x}}_{i}} \right)} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \sum\nolimits_{i = 1}^{{n_j}} {\frac{1}{{{n_j}}}{K_{{H_j}}}\left( {\boldsymbol{x} - {\boldsymbol{x}_i}} \right)} . \\ \end{align} $

(7)

2 实证分析 2.1 数据采集与预处理

本文数据来源于某商业银行信用中心的信用卡用户数据，该数据集样本总量为67 773个，其中每一个样本代表一个客户对应的信息。每个客户信息含有45个属性，表示本文选取的自变量为45个，包含客户的基本情况、个人金融标的资产、个人消费和个人贷款等方面(见附录表A1)。用一个标签属性对客户类别进行二分类，其中表示“好”的客户标签为“0”，即没有违约的客户；“坏”的客户标签为“1”，即有违约的客户。在这67 773个样本总量中，被定义为“好”的客户样本量有66 051个，占总样本量的97.5%，被定义为“坏”的客户样本量有1 722个，占总样本量的2.5%。

商业银行收集到的信用卡用户数据类别标签通常是严重非均衡的，同时数据也是严重缺失的，因为真正违约或数据信息完整的客户只有很少的一部分。由于样本数据集的质量直接决定了数据分析结果，因此，对样本数据集进行预处理是十分必要的。针对缺失数据进行预处理时，主要采用3种处理方法：删除法、填充法和不处理。本文采用常见的填充法来处理，对于数值型的缺失用该变量的均值填补，对于属性变量的缺失用“空”填补。

2.2 评价标准与模型建立

本文以判别能力和预测精度作为评价标准，对个人信用数据进行实证分析。采用ROC曲线(receiver operating characteristic curve)、AUC(area under the curve of ROC)值和KS(Kolmogorov-Smirnov)值进行验证。考虑到信用评分的本质是一个二分类问题，本文采用两类错误对模型预测结果的可靠性和精度进行解释。

ROC曲线^[29]是评估二元分类器效果的常用方法，也是辅助确定概率分割值的有效工具。一般ROC曲线的x轴为假正率(FPR), y轴为真正率(TPR)，二分类预测的混淆矩阵中，行项为观测的实际类别值，列项为预测类别值。一般给定一个二分类模型和它的阈值，就能从这些样本数据的真实值和预测值计算出一个坐标点。坐标点离左上角越近，表示其预测准确率越高；离右下角越近，表示其预测准确率越低。作为ROC曲线的补充，AUC值表示ROC曲线下方的面积。AUC值越大的分类器，其分类正确率越高; 这里的KS值仅代表模型分割样本的能力，并不能完全表示分割是否准确。在极端情况下，即便好坏客户完全分错，KS值也可以很高。但通常情况下，KS值大于0.2就可认为模型有比较好的预测准确性。

从两类错误角度考虑，第1类错误即将“好”的客户预测成为“坏”的客户，第2类错误即将“坏”的客户预测成为“好”的客户。虽然这两类错误都是我们所要避免的，但是在实际情况中，犯第2类错误所付出的代价是第1类错误的好几倍。因此，我们的主要目的是将整体错误率降低的同时，将第2类错误降到最低，以便将损失减少到最小。

2.2.1 Group-Lasso Logistic回归模型

采用Group-Lasso Logistic回归方法建立个人信用评分模型。由于该数据中含有大量的分类变量，所以不能直接用Lasso方法进行变量选择。因此，在这里采用Group-Lasso方法进行变量选择，对由分类变量产生的哑变量做同时变量选择。分别以子模型相对于饱和模型的偏差和AUC值作为模型选择的准则进行比较分析。

1) Group-Lasso Logistic回归模型(偏差准则)

以子模型相对于饱和模型的偏差作为模型选择的准则，做5折交叉验证，选择交叉验证偏差(CV deviance) 最小时对应的模型。偏差定义如下

$ D=-2\left( \log \left( p\left( y|{{{\hat{\boldsymbol{\beta} }}}_{0}} \right) \right)-\log \left( p\left( y|{{{\hat{\boldsymbol{\beta} }}}_{s}} \right) \right) \right), $

(8)

其中：$ {\boldsymbol{\hat \beta} _0} $是由子模型估计出的参数，$ {\boldsymbol{\hat \beta} _s} $是由饱和模型估计出的参数。参数λ与交叉验证偏差的关系见图 1。

得到最优参数λ=0.000 415，选出40个变量，剔除5个变量。用选出的40个变量训练Logistic回归模型，训练集和测试集对应的样本编号都与前文相同(通过固定随机种子实现)，得到在测试集上的ROC曲线(图 2)。由ROC曲线可得AUC值为0.777，经计算可得KS值为0.434 3。

2) Group-Lasso Logistic回归模型(AUC准则)

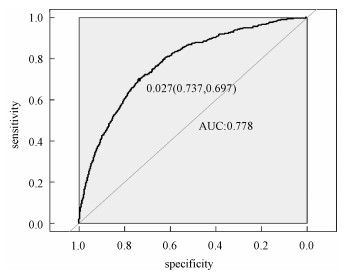
以AUC值作为模型选择的准则。在这里没有用到交叉验证，而是直接根据不同子模型在测试集上的AUC值选择AUC值最大时对应的模型。此时，模型选出39个变量，剔除6个变量。用选出的39个变量训练Logistic回归模型，训练集和测试集对应的样本编号都与前文相同(通过固定随机种子实现)，得到在测试集上的ROC曲线(图 3)。由ROC曲线可得：AUC值最大为0.778，经计算可得AUC值最大的模型对应的KS值为0.434 1。

实证结果表明，以偏差作为模型选择准则得到的结果，虽然“0”的准确率相对另一个模型有所下降，但是“1”的准确率比另一个模型有所提升，即降低了犯第2类错误的概率，同时KS值也略有提升，表明以偏差作为模型选择准则得到的结果更为有效。

2.2.2 ROSE Group-Lasso Logistic回归模型

1) ROSE Group-Lasso Logistic回归模型(偏差准则)

采用以偏差作为模型选择的准则选出的40个变量来建模。此时，训练集和测试集不变，其中训练集样本容量为40 664，标签为“0”的样本有39 631个，标签为“1”的样本有1 033个。通过采用ROSE方法产生均衡数据集，均衡数据集标签为“0”和“1”的样本分别为20 399个和20 265个，用均衡数据训练模型，得到在测试集上的ROC曲线(图 4)。由ROC曲线得到AUC值为0.78，经过计算得到KS值为0.434 5。

2) ROSE Group-Lasso Logistic回归模型(AUC准则)

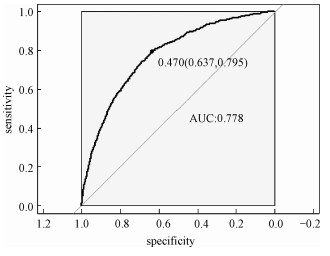
采用以AUC值作为模型选择的准则选出的39个变量来建模。此时，训练集和测试集不变，其中训练集样本容量为40 664，标签为“0”的样本有39 631个，标签为“1”的样本有1 033个。同样通过采用ROSE方法产生均衡数据集，均衡数据集标签为“0”和“1”的样本分别为20 399个和20 265个，用均衡数据训练模型，得到在测试集上的ROC曲线(图 5)。由ROC曲线得到AUC值为0.778，经过计算得到KS值为0.434 7。

实证结果表明，采用ROSE算法对样本数据进行非均衡处理之后，以AUC值作为模型选择准则得到的结果，虽然“0”的准确率相对于偏差作为模型选择准则有所下降，但是“1”的准确率比另一个模型大幅提升，即降低了犯第2类错误的概率，同时KS值也略有提升，因此，本文认为以AUC值作为模型选择准则得到的结果更为有效。

2.2.3 SMOTE Group-Lasso Logistic回归模型

1) SMOTE Group-Lasso Logistic回归模型(偏差准则)

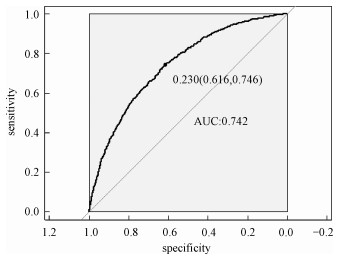
采用以偏差作为模型选择的准则选出的40个变量来建模，其他条件不变。得到在测试集上的ROC曲线(图 6)。由ROC曲线得到AUC值为0.742，经过计算得到KS值为0.416 7。

2) SMOTE Group-Lasso Logistic回归模型(AUC准则)

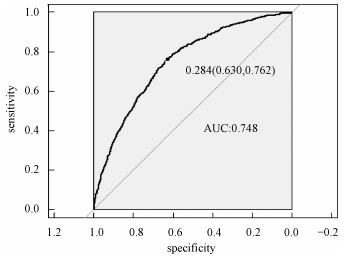
采用以AUC值作为模型选择的准则选出的39个变量来建模，其他条件不变。得到在测试集上的ROC曲线(图 7)。这里由ROC曲线得到AUC值为0.748，经过计算得到KS值为0.420 9。

实证结果表明，采用SMOTE算法进行样本数据非均衡处理，所得结果非常不理想。虽然两者都属于人造样本数据合成法，但显然SMOTE算法在这里并不适用。

2.3 各模型结果比较分析

本文以判别能力和预测精度作为评价标准，对个人信用数据进行分析，采用ROC曲线、AUC值和KS值进行验证。同时考虑到信用评分的本质是一个二分类问题，所以从两类错误角度进一步对模型结果预测的可靠性进行解释。通过比较上述几种模型结果(表 1)可以看出，相对于其他模型，本文构建的ROSE Group-Lasso Logistic回归模型(AUC准则)所得结果的AUC值和KS值都较高，说明该模型整体的预测精度有所提高，并且“1”的准确率大幅提升，即降低了犯第2类错误的概率。因此，基于ROSE Group-Lasso Logistic回归模型(AUC准则)构建的个人信用评分模型更为有效。

3 结论与展望

本文将Group-Lasso Logistic方法引入个人信用评分模型，主要创新点如下：1)样本数据来源于国内某商业银行信用卡中心，大量真实的样本数据使得实证结果更加具有实际参考价值；2)针对样本数据中违约客户与未违约客户的严重不均衡状况，创造性地采用ROSE算法对样本数据进行非均衡处理，提升了数据质量。最后，实证结果表明，ROSE Group-Lasso Logistic(AUC准则)方法在判别能力和预测能力上相对其他模型更为有效。因此，本文构建的信用评分模型，能够作为客户信用评价决策的有效依据，指导银行及其他金融机构评估顾客个人信用风险，并且在实际运用中也具有良好的可操作性。

本文的研究只是从统计方法上对个人信用评分模型进行实证探讨，具有局限性。未来的研究可以转向构建适合个人信用评分的动态评分模型。动态信用评分模型不仅可以进一步优化商业银行的信用风险管理，还能更加及时和精确地估计违约损失率。

附录A