Stochastic Poisson systems are defined as stochastic systems of the form[1]
| $ \begin{array}{c} \mathrm{d} \boldsymbol{X}(t)=\boldsymbol{B}(\boldsymbol{X})\left(\nabla H^{0}(\boldsymbol{X}) \mathrm{d} t+\sum\limits_{i=1}^{s} \nabla H^{i}(\boldsymbol{X}) \circ \mathrm{d} W^{i}(t)\right), \\ \boldsymbol{X}\left(t_{0}\right)=x, \end{array} $ | (1) |
where
| $ \begin{array}{c} \sum\limits_{l=1}^{n}\left(\frac{\partial b_{i j}(\boldsymbol{X})}{\partial \boldsymbol{X}_{l}} b_{l k}(\boldsymbol{X})+\frac{\partial b_{j k}(\boldsymbol{X})}{\partial \boldsymbol{X}_{l}} b_{l i}(\boldsymbol{X})+\right. \\ \left.\frac{\partial b_{k i}(\boldsymbol{X})}{\partial \boldsymbol{X}_{l}} b_{l j}(\boldsymbol{X})\right)=0, \end{array} $ | (2) |
for all i, j, k. It is called the structural matrix. Hi (i=0, …, s) are smooth scalar functions, and (W1(t), …, Ws(t)) is an s-dimensional standard Wiener process. The small circle "°" before d Wi denotes stochastic differential equations of Stratonovich sense.
If n=2d is even, and
It can be proved that[1], almost surely, the phase flow
| $ \frac{\partial \boldsymbol{X}(t)}{\partial \boldsymbol{x}} \boldsymbol{B}(\boldsymbol{x}) \frac{\partial \boldsymbol{X}(t)^{\mathrm{T}}}{\partial \boldsymbol{x}}=\boldsymbol{B}(\boldsymbol{X}(t)), \forall t \geqslant 0. $ | (3) |
As was given in Refs.[1, 5-7], etc., a function C(X) is called a Casimir function of a Poisson system with structural matrix B(X), if
| $ \nabla C(\boldsymbol{X})^{\mathrm{T}} \boldsymbol{B}(\boldsymbol{X}) \equiv 0, \text { for all } \boldsymbol{X}. $ | (4) |
It is not difficult to prove that (see Ref.[1]), the Casimir functions C(X) are invariants of the stochastic Poisson systems (1).
Numerical methods preserve the Poisson structure and the Casimir functions, namely, the methods {Xn} satisfying
| $ \begin{array}{l} \frac{\partial \boldsymbol{X}_{n+1}}{\partial \boldsymbol{X}_{n}} \boldsymbol{B}\left(\boldsymbol{X}_{n}\right) \frac{\partial {\boldsymbol{X}_{n+1}}^{\rm{T}}}{\partial \boldsymbol{X}_{n}}=\boldsymbol{B}\left(\boldsymbol{X}_{n+1}\right) ,\\ C\left(\boldsymbol{X}_{n+1}\right)=C\left(\boldsymbol{X}_{n}\right), \forall n \geqslant 0, \end{array} $ | (5) |
are called Poisson integrators[6]. Poisson integrators for deterministic Poisson systems have been developed from various points of view (see Refs.[5-7] and references therein). Numerical methods for stochastic Poisson systems, however, are still rarely studied, except in a number of recent papers on structure-preserving methods for certain special stochastic Poisson systems with single noise or/and even dimensions (e.g., Refs.[8-9]), as well as our paper (Ref.[1]) on numerical methods based on Darboux-Lie theorem for general stochastic Poisson systems.
In this paper, we consider linear stochastic Poisson systems of the form
| $ \begin{array}{l} \mathrm{d} \boldsymbol{X}(t)=\boldsymbol{B}\left(\nabla H^{0}(\boldsymbol{X}) \mathrm{d} t+\sum\limits_{i=1}^{s} \nabla H^{i}(\boldsymbol{X}) \circ \mathrm{d} W^{i}(t)\right), \\ \boldsymbol{X}\left(t_{0}\right)=\boldsymbol{x}, \end{array} $ | (6) |
where
| $ \begin{array}{l} \mathrm{d} \boldsymbol{X}(t)=\boldsymbol{A}^{0} \boldsymbol{X} \mathrm{d} t+\sum\limits_{i=1}^{s} \boldsymbol{A}^{i} \boldsymbol{X} \circ \mathrm{d} W^{i}(t), \\ \boldsymbol{X}\left(t_{0}\right)=\boldsymbol{x}, \end{array} $ | (7) |
where
| $ \boldsymbol{A}^{i}=\boldsymbol{B C}^{i}, i=0, \cdots, s. $ |
The exact solution of (7) is of the form
| $ \begin{array}{l} \mathit{\boldsymbol{X}}(t) = \\ \exp \left[ {\left( {t - {t_0}} \right){\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\left( {{W^i}(t) - {W^i}\left( {{t_0}} \right)} \right)} {\mathit{\boldsymbol{A}}^i}} \right] \cdot \mathit{\boldsymbol{X}}\left( {{t_0}} \right). \end{array} $ | (8) |
On the analogy of the discussions for linear Hamiltonian systems in Refs. [5, 10-11], we need to simulate the random matrix exponential in (8) appropriately to obtain high order structure-preserving numerical solvers.
As mentioned above, as
In this paper, we apply Padé approximations to the random matrix exponential in (8), to produce stochastic Poisson integrators which preserve both the Poisson structure and the Casimir functions of the original linear stochastic Poisson systems (7) and possess high root mean-square accuracy. This is an extension of the above-mentioned Padé approximation approaches for linear Hamiltonian systems[5, 10-11] to linear stochastic Poisson context.
The contents of this paper are organized as follows. In section 1, we construct the numerical schemes based on the Padé approximations, namely, the (l, m) -schemes. In section 2 we analyze the root mean-square convergence orders of the proposed (l, m) -schemes. In section 3 we prove the preservation of the Poisson structure and the Casimir functions by the (p, p) -schemes, that is, the (l, m) -schemes when l=m=p. Numerical experiments are performed in section 4 to verify the theoretical analysis and illustrate the numerical behavior of the proposed schemes. Section 5 is a brief conclusion.
1 Numerical schemes based on the Padé approximationsTo simulate the random matrix exponential in (8), we can use the following Padé approximation (see e.g. Refs.[10, 12])
| $ \exp (\boldsymbol{M}) \approx \boldsymbol{P}_{l, m}(\boldsymbol{M})=\boldsymbol{D}_{l, m}^{-1}(\boldsymbol{M}) \boldsymbol{N}_{l, m}(\boldsymbol{M}), $ | (9) |
where M represents an n×n dimensional square matrix, l, m are positive integers, and
| $ \boldsymbol{D}_{l, m}(\boldsymbol{M})=\boldsymbol{I}+\sum\limits_{k=1}^{l} d_{k}^{l, m}(-\boldsymbol{M})^{k} , $ |
| $ \boldsymbol{N}_{l, m}(\boldsymbol{M})=\boldsymbol{I}+\sum\limits_{k=1}^{m} n_{k}^{l, m} \boldsymbol{M}^{k} $ |
with
| $ d_{k}^{l, m} =\frac{(l+m-k) ! l !}{(l+m) ! k !(l-k) !}, $ |
| $ n_{k}^{l, m} =\frac{(l+m-k) ! m !}{(l+m) ! k !(m-k) !}. $ |
The invertibility of the matrix Dl, m(M) can be ensured by e.g.
| $ \mid \exp (\boldsymbol{M})-\boldsymbol{P}_{l, m}(\boldsymbol{M}) \mid=O\left(|\boldsymbol{M}|^{l+m+1}\right). $ | (10) |
Now we construct the following numerical discretization for the linear stochastic Poisson system (7)
| $ \begin{array}{l} \mathit{\boldsymbol{X}}_{n + 1}^{l,m} = {\left[ {\mathit{\boldsymbol{I}} + \sum\limits_{k = 1}^l {d_k^{l,m}} {{\left( { - {\mathit{\boldsymbol{Z}}_n}} \right)}^k}} \right]^{ - 1}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\mathit{\boldsymbol{I}} + \sum\limits_{k = 1}^m {n_k^{l,m}} {{\left( {{\mathit{\boldsymbol{Z}}_n}} \right)}^k}} \right]\mathit{\boldsymbol{X}}_n^{l,m},\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{X}}_0^{l,m} = \mathit{\boldsymbol{x}}. \end{array} $ | (11) |
where
| $ {{\mathit{\boldsymbol{Z}}_n} = h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\left[ {{W^i}\left( {{t_{n + 1}}} \right) - {W^i}\left( {{t_n}} \right)} \right]} {\mathit{\boldsymbol{A}}^i},} $ |
| $ {{t_n} = {t_0} + nh.} $ |
Wi(tn+1)-Wi(tn) can be simulated by
| $ \zeta_{n, h}^{i}=\left\{\begin{array}{ll} \xi_{n}^{i}, & \left|\xi_{n}^{i}\right| \leqslant A_{h}, \\ A_{h}, & \xi_{n}^{i}>A_{h}, \\ -A_{h}, & \xi_{n}^{i}<-A_{h}, \end{array}\right. $ | (12) |
After the truncation (12), we rewrite the scheme (11) in the following form
| $ \begin{array}{l} \mathit{\boldsymbol{X}}_{n + 1}^{l,m} = \left[ { - \sum\limits_{k = 1}^l {d_k^{l,m}} {{\left( { - \overline {{\mathit{\boldsymbol{Z}}_n}} } \right)}^k}} \right]\mathit{\boldsymbol{X}}_{n + 1}^{l,m} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\mathit{\boldsymbol{I}} + \sum\limits_{k = 1}^m {n_k^{l,m}} \overline {\mathit{\boldsymbol{Z}}_n^k} } \right]\mathit{\boldsymbol{X}}_n^{l,m},\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{X}}_0^{l,m} = \mathit{\boldsymbol{x}}, \end{array} $ | (13) |
where
| $ \overline {{\mathit{\boldsymbol{Z}}_n}} = h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } \zeta _{n,h}^i{\mathit{\boldsymbol{A}}^i}. $ | (14) |
We can use fixed-point iterations to get
| $ \sqrt {h|\ln h|} < \min \left\{ {\frac{1}{{\sqrt {2c} }},\frac{1}{{\sqrt {2c} \cdot \mathop {\max }\limits_k \left\{ {d_k^{l,m}} \right\} \cdot {Q_l}}}} \right\}, $ | (15) |
with
Proposition 2.1[13] Suppose the one-step approximation
| $ \begin{array}{*{20}{c}} {\left| {E\left( {{\mathit{\boldsymbol{X}}_{t,x}}(t + h) - {{\mathit{\boldsymbol{\overline X}} }_{t,x}}(t + h)} \right)} \right|}\\ {\quad \le K{{\left( {1 + |\mathit{\boldsymbol{x}}{|^2}} \right)}^{1/2}}{h^{{p_1}}},}\\ {\begin{array}{*{20}{c}} {{{\left[ {E{{\left| {{\mathit{\boldsymbol{X}}_{t,x}}(t + h) - {{\mathit{\boldsymbol{\overline X}} }_{t,x}}(t + h)} \right|}^2}} \right]}^{1/2}}}\\ { \le K{{\left( {1 + |\mathit{\boldsymbol{x}}{|^2}} \right)}^{1/2}}{h^{{p_2}}}.} \end{array}} \end{array} $ | (16) |
Also, let
| $ p_{2} \geqslant \frac{1}{2}, p_{1} \geqslant p_{2}+\frac{1}{2}. $ | (17) |
Then for any N and k=0, 1, …, N the following inequality holds:
| $ \begin{array}{c} \left.\left.\left[E \mid \boldsymbol{X}_{t_{0}, X_{0}}\left(t_{k}\right)-\overline{\boldsymbol{X}}_{t_{0}, X_{0}}\left(t_{k}\right)\right)\right|^{2}\right]^{1 / 2} \\ \leqslant K\left(1+E\left|\boldsymbol{X}_{0}\right|^{2}\right)^{1 / 2} h^{p_{2}-1 / 2}, \end{array} $ | (18) |
i.e. the order of accuracy of the method constructed using the one-step approximation
Proposition 2.2[13] Let the one-step approximation
| $ \begin{array}{c} \left|E\left(\overline{\boldsymbol{X}}_{t, x}(t+h)-\widetilde{\boldsymbol{X}}_{t, x}(t+h)\right)\right|=O\left(h^{p_{1}}\right), \\ {\left[E\left|\overline{\boldsymbol{X}}_{t, x}(t+h)-\widetilde{\boldsymbol{X}}_{t, x}(t+h)\right|^{2}\right]^{1 / 2}=O\left(h^{p_{2}}\right)} \end{array} $ | (19) |
with the same hp1 and hp2. Then the method based on the one-step approximation
Using the above fundamental convergence theorem and its corollary, namely the Propositions 2.1 and 2.2, we can prove the following convergence theorem for the scheme (13).
Theorem 2.1 If l and m have the same parity, and the truncation parameter c in (12) satisfies c≥l+m, then the root mean-square convergence order of the (l, m) -scheme (13) is
Proof Consider the following scheme:
| $ \begin{array}{l} \overline{\boldsymbol{X}_{n+1}^{l, m}}=\overline{\boldsymbol{X}_{n}^{l, m}}+\left[\sum\limits_{j=1}^{l+m} \frac{1}{j !} \overline{\boldsymbol{Z}_{n}^{j}}\right] \overline{\boldsymbol{X}_{n}^{l, m}}, \\ \overline{\boldsymbol{X}_{0}^{l, m}}=\boldsymbol{x}, \end{array} $ | (20) |
which is based on the one-step approximation
| $\begin{array}{c} \overline{\boldsymbol{X}^{l, m}}(t+h ; t, \boldsymbol{x})=\boldsymbol{x}+ \\ \sum\limits_{j=1}^{l+m} \frac{1}{j !}\left(h \boldsymbol{A}^{0}+\sum\limits_{i=1}^{s} \sqrt{h} \zeta_{h}^{i} \boldsymbol{A}^{i}\right)^{j} \boldsymbol{x}, \end{array} $ | (21) |
where ζhi is the truncation of the N(0, 1) random variable ξi that makes
| $ \boldsymbol{X}(t+h ; t, \boldsymbol{x})=\boldsymbol{x}+\sum\limits_{j=1}^{+\infty} \frac{1}{j !}\left(h \boldsymbol{A}^{0}+\sum\limits_{i=1}^{s} \sqrt{h} \xi^{i} \boldsymbol{A}^{i}\right)^{j} \boldsymbol{x} . $ | (22) |
Then we can derive
| $ \begin{array}{l} \begin{array}{*{20}{l}} {\left| {E\left( {\mathit{\boldsymbol{X}}(t + h;t,\mathit{\boldsymbol{x}}) - \overline {{\mathit{\boldsymbol{X}}^{l,m}}} (t + h;t,\mathit{\boldsymbol{x}})} \right)} \right|}\\ { \le |E\left[ {\sum\limits_{j = 1}^{l + m} {\frac{1}{{j!}}} {{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } {\xi ^i}{\mathit{\boldsymbol{A}}^i}} \right)}^j} - } \right.} \end{array}\\ \begin{array}{*{20}{c}} {\sum\limits_{j = 1}^{l + m} {\frac{1}{{j!}}} {{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } \zeta _h^i{\mathit{\boldsymbol{A}}^i}} \right)}^j} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\sum\limits_{j = l + m + 1}^{ + \infty } {\frac{1}{{j!}}} {{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } {\xi ^i}{\mathit{\boldsymbol{A}}^i}} \right)}^j}} \right]| \cdot |\mathit{\boldsymbol{x}}|}\\ { \le {{\left( {1 + |\mathit{\boldsymbol{x}}{|^2}} \right)}^{\frac{1}{2}}}\left( {{L_1} + {L_2} + {L_3}} \right),} \end{array} \end{array} $ | (23) |
where
| $ \begin{array}{*{20}{l}} {{L_1} = \sum\limits_{j = 1}^{l + m} {\frac{1}{{j!}}} }\\ {\left| {E\left[ {{{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } {\xi ^i}{\mathit{\boldsymbol{A}}^i}} \right)}^j} - {{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } \zeta _h^i{\mathit{\boldsymbol{A}}^i}} \right)}^j}} \right]} \right|,} \end{array} $ |
| $ {{L_2} = \frac{1}{{(l + m + 1)!}}\left| {E{{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } {\xi ^i}{\mathit{\boldsymbol{A}}^i}} \right)}^{(l + m + 1)}}} \right|,} $ |
| $ {{L_3} = \sum\limits_{j = l + m + 2}^{ + \infty } {\frac{1}{{j!}}} \left| {E{{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } {\xi ^i}{\mathit{\boldsymbol{A}}^i}} \right)}^j}} \right|.} $ |
Due to the fact that, for square matrices Mi (i=0, …, s), and any
| $ \left(\sum\limits_{i=0}^{s} \boldsymbol{M}^{i}\right)^{j}=\sum\limits_{\sigma_{1}, \cdots, \sigma_{j} \in\{0,1, \cdots, s\}} \boldsymbol{M}^{\sigma_{1}} \cdots \boldsymbol{M}^{\sigma_{j}}, $ |
and
| $ \begin{array}{l} {L_1} \le \left. {\sum\limits_{j = 1}^{l + m} {\frac{1}{{j!}}} {h^{\frac{j}{2}}}} \right|E\sum\limits_{{\sigma _1}, \cdots ,{\sigma _j} \in \{ 0, \cdots ,s\} } {} \\ \left. {{\mathit{\boldsymbol{A}}^{{\sigma _1}}} \cdots {\mathit{\boldsymbol{A}}^{{\sigma _j}}}\left( {{\xi ^{{\sigma _1}}} \cdots {\xi ^{{\sigma _j}}} - \zeta _h^{{\sigma _1}} \cdots \zeta _h^{{\sigma _j}}} \right)} \right|\\ \le \sum\limits_{j = 1}^{l + m} {\frac{1}{{j!}}} {h^{\frac{j}{2}}}\mathop {\max }\limits_{0 \le i \le s} {\left| {{\mathit{\boldsymbol{A}}^i}} \right|^j}\sum\limits_{{\sigma _1}, \cdots ,{\sigma _j} \in \{ 0, \cdots ,s\} } \mid E\left( {{\xi ^{{\sigma _1}}} \cdots {\xi ^{{\sigma _j}}} - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\zeta _h^{{\sigma _1}} \cdots \zeta _h^{{\sigma _j}}} \right)} \right|\\ = \sum\limits_{j = 1}^{l + m} {\frac{1}{{j!}}} {h^{\frac{j}{2}}}\mathop {\max }\limits_{0 \le i \le s} {\left| {{\mathit{\boldsymbol{A}}^i}} \right|^j}\sum\limits_{0 < {\rho _1} + \cdots + {\rho _s} \le j} {} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {E\left[ {{{\left( {{\xi ^1}} \right)}^{{\rho _1}}} \cdots {{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - {{\left( {\zeta _h^1} \right)}^{{\rho _1}}} \cdots {{\left( {\zeta _h^s} \right)}^{{\rho _s}}}} \right]} \right|, \end{array} $ |
where
Obviously,
| $ \begin{array}{l} {P_2} \le \frac{{{K_0}}}{{(l + m + 1)!}}{h^{\frac{{l + m + 1}}{2}}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {E\sum\limits_{{\sigma _1}, \cdots ,{\sigma _{l + m + 1}} \in \{ 1, \cdots ,s\} } {{\mathit{\boldsymbol{A}}^{{\sigma _1}}} \cdots {\mathit{\boldsymbol{A}}^{{\sigma _{l + m + 1}}}}{\xi ^{{\sigma _1}}} \cdots {\xi ^{{\sigma _{l + m + 1}}}}} } \right|\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \le \frac{{{K_0}}}{{(l + m + 1)!}}{h^{\frac{{l + m + 1}}{2}}}\mathop {\max }\limits_{1 \le i \le s} {\left| {{\mathit{\boldsymbol{A}}^i}} \right|^{l + m + 1}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} {\sum\limits_{{\sigma _1}, \cdots ,{\sigma _{l + m + 1}} \in \{ 1, \cdots ,s\} } {\left| {E\left( {{\xi ^{{\sigma _1}}} \cdots {\xi ^{{\sigma _{l + m + 1}}}}} \right)} \right|} }\\ { = \frac{{{K_0}}}{{(l + m + 1)!}}{h^{\frac{{l + m + 1}}{2}}}\mathop {\max }\limits_{1 \le i \le s} {{\left| {{\mathit{\boldsymbol{A}}^i}} \right|}^{l + m + 1}}}\\ {\sum\limits_{{\rho _1} + \cdots + {\rho _s} = l + m + 1} {\left| {E\left[ {{{\left( {{\xi ^1}} \right)}^{{\rho _1}}} \cdots {{\left( {{\xi ^s}} \right)}^{{\rho _s}}}} \right]} \right|,} } \end{array} \end{array} $ |
where K0 is a positive constant independent of h. Then, if l+m+1 is odd, due to independence of ξ1, …, ξs, we have P2=0 which implies
According to the distributions of ξi and ζhi, and let t=x-Ah, we have for any
| $ \begin{array}{l} \left| {E\left[ {{{\left( {{\xi ^i}} \right)}^\rho } - {{\left( {\zeta _h^i} \right)}^\rho }} \right]} \right|\\ = 2\left| {\int\limits_{{A_h}}^{ + \infty } {\left( {{x^\rho } - A_h^\rho } \right)} \exp \left( { - \frac{{{x^2}}}{2}} \right){\rm{d}}x} \right|\\ \le 2\left| {\sum\limits_{u = 0}^{\rho - 1} {C_\rho ^u} A_h^u\exp \left( { - \frac{{A_h^2}}{2}} \right)\int\limits_0^{ + \infty } {{t^{\rho - u}}} \exp \left( { - \frac{{{t^2}}}{2}} \right){\rm{d}}t} \right|\\ \le 2{K_1}\left| {\sum\limits_{u = 0}^{\rho - 1} {A_h^u} \exp \left( { - \frac{{A_h^2}}{2}} \right)} \right|, \end{array} $ | (24) |
where
| $ {K_1} = \mathop {\max }\limits_{0 \le u \le \rho - 1} C_\rho ^u\rho !\sqrt {{\rm{ \mathsf{ π} }}/2} , $ |
and the last inequality is due to
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int\limits_0^{ + \infty } {{t^\nu }} \exp \left( { - \frac{{{t^2}}}{2}} \right){\rm{d}}t\\ = \left\{ {\begin{array}{*{20}{l}} {(\nu - 1)(\nu - 3) \cdots 4 \times 2,}&{\nu {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{is}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{odd, }}}\\ {(\nu - 1)(\nu - 3) \cdots 5 \times 3\sqrt {{\rm{ \mathsf{ π} }}/2} ,}&{\nu {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{is}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{even, }}} \end{array}} \right. \end{array} $ |
for ν=ρ-u which satisfies 1≤ν≤ρ.
Since
| $ \left|E\left[\left(\xi^{i}\right)^{\rho}-\left(\zeta_{h}^{i}\right)^{\rho}\right]\right| \leqslant 2 K_{1} K_{2} h^{\frac{1-\rho}{2}+l+m} $ | (25) |
for i=1, …, s. Note that K1, K2 are positive constants independent of h.
On the other hand,
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{\rm{|E}}\left[ {{{\left( {{\xi ^{\rm{1}}}} \right)}^{{\rho _{\rm{1}}}}}{{\left( {{\xi ^{\rm{2}}}} \right)}^{{\rho _{\rm{2}}}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^{\rm{s}}}} \right)}^{{\rho _{\rm{s}}}}}{\rm{ - }}} \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {\zeta _h^2} \right)}^{{\rho _2}}} \cdots {{\left( {\zeta _h^{s - 1}} \right)}^{{\rho _{s - 1}}}}{{\left( {\zeta _h^s} \right)}^{{\rho _s}}}} \right]\mid }\\ { \le \mid E\left[ {{{\left( {{\xi ^1}} \right)}^{{\rho _1}}}{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}}} \right]\mid + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mid E\left[ {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {\zeta _h^2} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}}} \right]\mid + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mid E\left[ {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {\zeta _h^2} \right)}^{{\rho _2}}} \cdots {{\left( {\zeta _h^{s - 1}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {\zeta _h^2} \right)}^{{\rho _2}}} \cdots {{\left( {\zeta _h^{s - 1}} \right)}^{{\rho _{s - 1}}}}{{\left( {\zeta _h^s} \right)}^{{\rho _s}}}} \right]\mid \\ = E\left[ {{{\left( {{\xi ^1}} \right)}^{{\rho _1}}} - {{\left( {\zeta _h^1} \right)}^{{\rho _1}}}} \right]\mid \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mid E\left[ {{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}}} \right]\mid + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mid E\left[ {{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} - {{\left( {\zeta _h^2} \right)}^{{\rho _2}}}} \right]\mid \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mid E\left[ {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}}} \right]\mid + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots + \\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {E\left[ {{{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - {{\left( {\zeta _h^s} \right)}^{{\rho _s}}}} \right]} \right| \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {E\left[ {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}} \cdots {{\left( {\zeta _h^{s - 1}} \right)}^{{\rho _{s - 1}}}}} \right]} \right|.} \end{array} \end{array} $ | (26) |
From (25) we know that
| $ \left|E\left[\left(\xi^{i}\right)^{\rho}-\left(\zeta_{h}^{i}\right)^{\rho}\right]\right|=O\left(h^{\frac{1-\rho}{2}+l+m}\right), $ |
which, together with (26), implies that
| $ L_{1}=O\left(h^{l+m+\frac{1}{2}}\right). $ | (27) |
We have analyzed the order of L2 above. In addition,
| $ \begin{array}{c} \left|E\left(\boldsymbol{X}(t+h ; t, \boldsymbol{x})-\overline{\boldsymbol{X}^{l, m}}(t+h ; t, \boldsymbol{x})\right)\right| \\ \left.\leqslant K\left(1+|\boldsymbol{x}|^{2}\right)^{1 / 2} h^{\left\lceil\frac{l+m+1}{2}\right\rceil}\right.. \end{array} $ | (28) |
where K is a positive constant independent of h, and
Now we estimate the second moment of the error. Applying the inequality
| $ E\left|\sum\limits_{i=1}^{k} a_{i}\right|^{2} \leqslant k\left(\sum\limits_{i=1}^{k} E\left|a_{i}\right|^{2}\right) $ | (29) |
we have
| $ \begin{array}{l} E\left|\boldsymbol{X}(t+h ; t, \boldsymbol{x})-\overline{\boldsymbol{X}^{l, m}}(t+h ; t, \boldsymbol{x})\right|^{2} \\ E \mid \sum\limits_{j=1}^{l+m} \frac{1}{j !}\left(h \boldsymbol{A}^{0}+\sum\limits_{i=1}^{s} \sqrt{h} \xi^{i} \boldsymbol{A}^{i}\right)^{j}-\\ \ \ \ \ \ \sum\limits_{j=1}^{l+m} \frac{1}{j !}\left(h \boldsymbol{A}^{0}+\sum\limits_{i=1}^{s} \sqrt{h} \zeta_{h}^{i} \boldsymbol{A}^{i}\right)^{j}+\\ \ \ \ \ \ \left.\sum\limits_{j=l+m+1}^{+\infty} \frac{1}{j !}\left(h \boldsymbol{A}^{0}+\sum\limits_{i=1}^{s} \sqrt{h} \xi^{i} \boldsymbol{A}^{i}\right)^{j}\right|^{2} \cdot|\boldsymbol{x}|^{2} \\ \leqslant 3|\boldsymbol{x}|^{2}\left(L_{4}+L_{5}+L_{6}\right), \end{array} $ | (30) |
where
| $ \begin{array}{l} {{L_4} = E\left| {\sum\limits_{j = 1}^{l + m} {\frac{1}{{j!}}} \left[ {{{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } {\xi ^i}{\mathit{\boldsymbol{A}}^i}} \right)}^j} - } \right.} \right.}\\ \ \ \ \ \ \ \ \ {{{\left. {\left. {{{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } \zeta _h^i{\mathit{\boldsymbol{A}}^i}} \right)}^j}} \right]} \right|}^2},} \end{array} $ |
| $ \begin{array}{l} {{L_5} = E\left| {\frac{1}{{(l + m + 1)!}}} \right.}\\ \ \ \ \ \ \ \ \ {{{\left. {{{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } {\xi ^i}{\mathit{\boldsymbol{A}}^i}} \right)}^{(l + m + 1)}}} \right|}^2},} \end{array} $ |
| $ {{L_6} = E{{\left| {\sum\limits_{j = l + m + 2}^{ + \infty } {\frac{1}{{j!}}} {{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } {\xi ^i}{\mathit{\boldsymbol{A}}^i}} \right)}^j}} \right|}^2}.} $ |
Again setting ξ0=1, ζh0=1, and applying (29) we have
| $ \begin{array}{l} {L_4} \le (l + m)\sum\limits_{j = 1}^{l + m} {\frac{1}{{{{(j!)}^2}}}} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E{\left| {{{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } {\xi ^i}{\mathit{\boldsymbol{A}}^i}} \right)}^j} - {{\left( {h{\mathit{\boldsymbol{A}}^0} + \sum\limits_{i = 1}^s {\sqrt h } \zeta _h^i{\mathit{\boldsymbol{A}}^i}} \right)}^j}} \right|^2}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \le (l + m)\sum\limits_{j = 1}^{l + m} {\frac{1}{{{{(j!)}^2}}}} {h^j}E\mid \sum\limits_{{\sigma _1}, \cdots ,{\sigma _j} \in \{ 0, \cdots ,s\} } {} \\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{A}}^{{\sigma _1}}} \cdots {\mathit{\boldsymbol{A}}^{{\sigma _j}}}\left( {{\xi ^{{\sigma _1}}} \cdots {\xi ^{{\sigma _j}}} - \zeta _h^{{\sigma _1}} \cdots \zeta _h^{{\sigma _j}}} \right)} \right|^2}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \le (l + m)\sum\limits_{j = 1}^{l + m} {\frac{{{{(s + 1)}^j}}}{{{{(j!)}^2}}}} \mathop {\max }\limits_{0 \le i \le s} {\left| {{\mathit{\boldsymbol{A}}^i}} \right|^{2j}}{h^j}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{{\sigma _1}, \cdots ,{\sigma _j} \in \{ 0, \cdots ,s\} } E {\left| {{\xi ^{{\sigma _1}}} \cdots {\xi ^{{\sigma _j}}} - \zeta _h^{{\sigma _1}} \cdots \zeta _h^{{\sigma _j}}} \right|^2}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = (l + m)\sum\limits_{j = 1}^{l + m} {\frac{{{{(s + 1)}^j}}}{{{{(j!)}^2}}}} \mathop {\max }\limits_{0 \le i \le s} {\left| {{\mathit{\boldsymbol{A}}^i}} \right|^{2j}}{h^j}\sum\limits_{0 < {\rho _1} + \cdots + {\rho _s} \le j} {} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E{\left| {{{\left( {{\xi ^1}} \right)}^{{\rho _1}}} \cdots {{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - {{\left( {\zeta _h^1} \right)}^{{\rho _1}}} \cdots {{\left( {\zeta _h^s} \right)}^{{\rho _s}}}} \right|^2}. \end{array} $ |
Meanwhile, it is easy to see that
| $ \begin{array}{l} {P_5} \le {K_3}{h^{l + m + 1}}E\mid \sum\limits_{{\sigma _1}, \cdots ,{\sigma _{l + m + 1}} \in \{ 1, \cdots ,s\} } {} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left. {{\kern 1pt} {\mathit{\boldsymbol{A}}^{{\sigma _1}}} \cdots {\mathit{\boldsymbol{A}}^{{\sigma _{l + m + 1}}}}{\xi ^{{\sigma _1}}} \cdots {\xi ^{{\sigma _{l + m + 1}}}}} \right|^2}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \le {K_3}{h^{l + m + 1}}{s^{l + m + 1}}\mathop {\max }\limits_{1 \le i \le s} {\left| {{\mathit{\boldsymbol{A}}^i}} \right|^{2(l + m + 1)}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{{\sigma _1}, \cdots ,{\sigma _{l + m + 1}} \in \{ 1, \cdots ,s\} } E {\left| {{\xi ^{{\sigma _1}}} \cdots {\xi ^{{\sigma _{l + m + 1}}}}} \right|^2}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {K_3}{h^{l + m + 1}}{s^{l + m + 1}}\mathop {\max }\limits_{1 \le i \le s} {\left| {{\mathit{\boldsymbol{A}}^i}} \right|^{2(l + m + 1)}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{{\rho _1} + \cdots + {\rho _s} = l + m + 1} E {\left| {{{\left( {{\xi ^1}} \right)}^{{\rho _1}}} \cdots {{\left( {{\xi ^s}} \right)}^{{\rho _s}}}} \right|^2}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = O\left( {{h^{l + m + 1}}} \right), \end{array} $ |
where K3 is a positive constant independent of h. Thus
Similar to the analysis for (25), let t=x-Ah, we have for any
| $ \begin{array}{l} E\left|\left(\xi^{i}\right)^{\rho}-\left(\zeta_{h}^{i}\right)^{\rho}\right|^{2} \\ =2 \int_{A_{h}}^{+\infty}\left(x^{\rho}-A_{h}^{\rho}\right)^{2} \exp \left(-\frac{x^{2}}{2}\right) \mathrm{d} x \\ =2 \int_{0}^{+\infty}\left(\sum\limits_{u=0}^{\rho-1} C_{\rho}^{u} A_{h}^{u} t^{\rho-u}\right)^{2} \exp \left(-\frac{\left(t+A_{h}\right)^{2}}{2}\right) \mathrm{d} t \\ \leqslant 2 \int_{0}^{+\infty} \rho\left(\sum\limits_{u=0}^{\rho-1}\left(C_{\rho}^{u}\right)^{2} A_{h}^{2 u} t^{2 \rho-2 u}\right) \exp \left(-\frac{\left(t+A_{h}\right)^{2}}{2}\right) \mathrm{d} t \\ \leqslant 2 \rho \sum\limits_{u=0}^{\rho-1}\left(C_{\rho}^{u}\right)^{2} A_{h}^{2 u} \exp \left(-\frac{A_{h}^{2}}{2}\right) \\ \quad \int_{0}^{+\infty} t^{2 \rho-2 u} \exp \left(-\frac{t^{2}}{2}\right) \mathrm{d} t \\ \leqslant 2 \rho K_{4} \sum\limits_{u=0}^{\rho-1}\left(C_{\rho}^{u}\right)^{2} A_{h}^{2 u} \exp \left(-\frac{A_{h}^{2}}{2}\right) \\ \leqslant 2 \rho K_{5} h^{1-\rho+l+m}, \end{array} $ | (31) |
for i=1, …, s, where K4, K5 are positive constants independent of h.
For L4, we have
| $ \begin{array}{l} \begin{array}{*{20}{l}} {\frac{1}{s}E\mid {{\left( {{\xi ^1}} \right)}^{{\rho _1}}}{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left. {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {\zeta _h^2} \right)}^{{\rho _2}}} \cdots {{\left( {\zeta _h^{s - 1}} \right)}^{{\rho _{s - 1}}}}{{\left( {\zeta _h^s} \right)}^{{\rho _s}}}} \right|}^2}}\\ { \le E\mid {{\left( {{\xi ^1}} \right)}^{{\rho _1}}}{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left. {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}}} \right|}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E\mid {{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left. {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {\zeta _h^2} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}}} \right|}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots + } \end{array}\\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E\mid {{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {\zeta _h^2} \right)}^{{\rho _2}}} \cdots {{\left( {\zeta _h^{s - 1}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left. {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}}{{\left( {\zeta _h^2} \right)}^{{\rho _2}}} \cdots {{\left( {\zeta _h^{s - 1}} \right)}^{{\rho _{s - 1}}}}{{\left( {\zeta _h^s} \right)}^{{\rho _s}}}} \right|}^2}}\\ { = E{{\left| {{{\left( {{\xi ^1}} \right)}^{{\rho _1}}} - {{\left( {\zeta _h^1} \right)}^{{\rho _1}}}} \right|}^2} \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E{{\left| {{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}}} \right|}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E{{\left| {{{\left( {{\xi ^2}} \right)}^{{\rho _2}}} - {{\left( {\zeta _h^2} \right)}^{{\rho _2}}}} \right|}^2} \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E{{\left| {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}} \cdots {{\left( {{\xi ^{s - 1}}} \right)}^{{\rho _{s - 1}}}}{{\left( {{\xi ^s}} \right)}^{{\rho _s}}}} \right|}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E{{\left| {{{\left( {{\xi ^s}} \right)}^{{\rho _s}}} - {{\left( {\zeta _h^s} \right)}^{{\rho _s}}}} \right|}^2} \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E{{\left| {{{\left( {\zeta _h^1} \right)}^{{\rho _1}}} \cdots {{\left( {\zeta _h^{s - 1}} \right)}^{{\rho _{s - 1}}}}} \right|}^2}.} \end{array} \end{array} $ | (32) |
From (31) we know that for i∈{1, …, s},
| $ L_{4} \leqslant O\left(h^{l+m+1}\right), $ | (33) |
Considering also the orders of L5 and L6 discussed above, we obtain
| $ \begin{array}{c} {\left[ {E{{\left| {\mathit{\boldsymbol{X}}(t + h;t,\mathit{\boldsymbol{x}}) - \overline {{\mathit{\boldsymbol{X}}^{l,m}}} (t + h;t,\mathit{\boldsymbol{x}})} \right|}^2}} \right]^{1/2}}\\ \le L{\left( {1 + |\mathit{\boldsymbol{x}}{|^2}} \right)^{1/2}}{h^{\frac{{l + m + 1}}{2}}}, \end{array} $ | (34) |
where L is a positive constant independent of h.
Applying Proposition 2.1, for the case that l and m have the same parity, we have
Next we consider the difference:
| $ \begin{array}{l} \boldsymbol{X}^{l, m}(t+h ; t, \boldsymbol{x})-\overline{\boldsymbol{X}}^{l, m}(t+h ; t, \boldsymbol{x}) \\ =\left(\boldsymbol{X}^{l, m}(t+h ; t, \boldsymbol{x})-\exp (\overline{\boldsymbol{Z}}) \boldsymbol{x}\right)- \\ \quad\left(\overline{\boldsymbol{X}^{l, m}}(t+h ; t, \boldsymbol{x})-\exp (\overline{\boldsymbol{Z}}) \boldsymbol{x}\right) \\ =\sum\limits_{j=2 p+1}^{+\infty} \overline{c_{j} \boldsymbol{Z}^{j}} \boldsymbol{x}, \end{array} $ | (35) |
where
| $ \overline{\boldsymbol{Z}}=h \boldsymbol{A}^{0}+\sum\limits_{i=1}^{s} \sqrt{h} \zeta_{h}^{i} \boldsymbol{A}^{i}, $ | (36) |
| $ \begin{array}{l} \left|E\left(\boldsymbol{X}^{l, m}(t+h ; t, \boldsymbol{x})-\overline{\boldsymbol{X}^{l, m}}(t+h ; t, \boldsymbol{x})\right)\right| \\ \leqslant \bar{K}_{1}\left|E \sum\limits_{j=l+m+1}^{+\infty}\left(h \boldsymbol{A}^{0}+\sum\limits_{i=1}^{s} \sqrt{h} \zeta_{h}^{i} \boldsymbol{A}^{i}\right)^{j}\right| \\ =O\left(h^{\frac{l+m}{2}+1}\right), \end{array} $ | (37) |
and
| $ \begin{array}{l} E\left|\boldsymbol{X}^{l, m}(t+h ; t, \boldsymbol{x})-\overline{X^{l, m}}(t+h ; t, \boldsymbol{x})\right|^{2}\\ \leqslant \bar{K}_{2} E\left|\sum\limits_{j=l+m+1}^{+\infty}\left(h \boldsymbol{A}^{0}+\sum\limits_{i=1}^{s} \sqrt{h} \zeta_{h}^{i} \boldsymbol{A}^{i}\right)^{j}\right|^{2} \\ =O\left(h^{l+m+1}\right) \end{array} $ | (38) |
where K1 and K2 are positive constants independent of h. Applying Proposition 2.2 we complete the proof of Theorem 2.1.
3 Preservation of the Poisson structure and the Casimir functionsFor the
Proposition 3.1 For any
| $ \overline{\boldsymbol{Z}_{n}}^{2 n} \boldsymbol{B} =\boldsymbol{B}\left(\overline{{\boldsymbol{Z}_{n}}^{2 n}}\right)^{\mathrm{T}} , $ |
| $ {{\boldsymbol { Z }} _ { n }}^{2 n+1} \boldsymbol{B} =-\boldsymbol{B}\left(\overline{\boldsymbol{Z}_{n}^{2 n+1}}\right)^{\mathrm{T}}. $ |
Proposition 3.2 Suppose f(x) is an even polynomial and g(x) is an odd polynomial, then we have
| $ f\left(\overline{{\boldsymbol{Z}}_{n}}\right) \boldsymbol{B}=\boldsymbol{B} f\left(\overline{{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right), g\left(\overline{{\boldsymbol{Z}}_{n}}\right) \boldsymbol{B}=-\boldsymbol{B} g\left(\overline{{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right), $ |
| $ \begin{array}{c} \left(f\left(\overline{\boldsymbol{Z}}_{n}\right)-g\left(\overline{\boldsymbol{Z}}_{n}\right)\right)\left(f\left(\overline{\boldsymbol{Z}}_{n}\right)+g\left(\overline{\boldsymbol{Z}}_{n}\right)\right) \boldsymbol{B} \\ =\left(f\left(\overline{\boldsymbol{Z}}_{n}\right)+g\left(\overline{\boldsymbol{Z}}_{n}\right)\right)\left(f\left(\overline{\boldsymbol{Z}}_{n}\right)-g\left(\overline{\boldsymbol{Z}}_{n}\right)\right) \boldsymbol{B}. \end{array} $ |
Now we prove the following theorem:
Theorem 3.1 The (p, p) -schemes (13) (l=m=p) preserve the Poisson structure of the original linear stochastic Poisson system (7).
Proof Regarding the equivalent form (11) of (13), we need to verify
| $ \begin{aligned} &\frac{\partial \boldsymbol{X}_{n+1}^{p, p}}{\partial \boldsymbol{X}_{n}^{p, p}} \boldsymbol{B}\left(\frac{\partial \boldsymbol{X}_{n+1}^{p, p}}{\partial \boldsymbol{X}_{n}^{p, p}}\right)^{\mathrm{T}}\\ &=\boldsymbol{D}_{p, p}^{-1}\left(\overline{\boldsymbol{Z}}_{n}\right) \boldsymbol{N}_{p, p}\left(\overline{\boldsymbol{Z}}_{n}\right) \boldsymbol{B} \boldsymbol{N}_{p, p}\left({\overline{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right) \boldsymbol{D}_{p, p}^{-1}\left({\overline{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right)\\ &=\boldsymbol{B}, \end{aligned} $ | (39) |
which is equivalent to
| $ \boldsymbol{N}_{p, p}\left(\overline{\boldsymbol{Z}}_{n}\right) \boldsymbol{B} \boldsymbol{N}_{p, p}\left({\overline{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right)=\boldsymbol{D}_{p, p}\left(\overline{\boldsymbol{Z}}_{n}\right) \boldsymbol{B} \boldsymbol{D}_{p, p}\left({\overline{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right). $ | (40) |
Let
| $ N_{p, p}\left(\bar{\boldsymbol{Z}}_{n}\right)=f\left(\bar{\boldsymbol{Z}}_{n}\right)+g\left(\bar{\boldsymbol{Z}}_{n}\right), $ |
| $ D_{p, p}\left(\bar{\boldsymbol{Z}}_{n}\right)=f\left(\bar{\boldsymbol{Z}}_{n}\right)-g\left(\bar{\boldsymbol{Z}}_{n}\right), $ |
where f(x) is an even polynomial and g(x) is an odd polynomial. Then it follows
| $ \begin{aligned} & \boldsymbol{N}_{p, p}\left(\overline{\boldsymbol{Z}}_{n}\right) \boldsymbol{B} \boldsymbol{N}_{p, p}\left({\overline{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right) \\ =&\left(f\left(\overline{\boldsymbol{Z}}_{n}\right)+g\left(\overline{\boldsymbol{Z}}_{n}\right)\right) \boldsymbol{B}\left(f\left({\overline{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right)+g\left({\overline{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right)\right) \\ =&\left(f\left(\overline{\boldsymbol{Z}}_{n}\right)+g\left(\overline{\boldsymbol{Z}}_{n}\right)\right)\left(f\left({\overline{\boldsymbol{Z}}_{n}}\right)-g\left(\overline{\boldsymbol{Z}}_{n}\right)\right) \boldsymbol{B} \\ =&\left(f\left(\overline{\boldsymbol{Z}}_{n}\right)-g\left(\overline{\boldsymbol{Z}}_{n}\right)\right)\left(f\left(\overline{\boldsymbol{Z}}_{n}\right)+g\left(\overline{\boldsymbol{Z}}_{n}\right)\right) \boldsymbol{B} \\ =&\left(f\left(\overline{\boldsymbol{Z}}_{n}\right)-g\left(\overline{\boldsymbol{Z}}_{n}\right)\right) \boldsymbol{B}\left(f\left({\overline{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right)-g\left({\overline{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right)\right) \\ =& \boldsymbol{D}_{p, p}\left(\overline{\boldsymbol{Z}}_{n}\right) \boldsymbol{B} \boldsymbol{D}_{p, p}\left({\overline{\boldsymbol{Z}}_{n}}^{\mathrm{T}}\right). \end{aligned} $ |
Next we prove the Casimir-preservation by the (p, p) -scheme (13).
Theorem 3.2 The (p, p) -schemes (13) (l=m=p) preserve the Casimir functions of the linear stochastic Poisson system (7).
Proof From (13) we know
| $ \boldsymbol{X}_{n+1}^{p, p}-\boldsymbol{X}_{n}^{p, p}=\boldsymbol{B} \boldsymbol{\varTheta}_{n}^{p, p}, $ |
where
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_n^{p,p} = \left( {\sum\limits_{k = 1}^p {n_k^{p,p}} \overline {{\mathit{\boldsymbol{Y}}_n}} {{\left( {\mathit{\boldsymbol{B}}\overline {{\mathit{\boldsymbol{Y}}_n}} } \right)}^{k - 1}}} \right)\mathit{\boldsymbol{X}}_n^{p,p} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\sum\limits_{k = 1}^p {d_k^{p,p}} {{( - 1)}^k}\overline {{\mathit{\boldsymbol{Y}}_n}} {{\left( {\mathit{\boldsymbol{B}}\overline {{\mathit{\boldsymbol{Y}}_n}} } \right)}^{k - 1}}} \right)\mathit{\boldsymbol{X}}_{n + 1}^{p,p}, \end{array} $ |
with
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} C\left( {\mathit{\boldsymbol{X}}_{n + 1}^{p,p}} \right) - C\left( {\mathit{\boldsymbol{X}}_n^{p,p}} \right)\\ = \int\limits_0^1 \nabla C{\left( {\mathit{\boldsymbol{X}}_n^{p,p} + \tau \left( {\mathit{\boldsymbol{X}}_{n + 1}^{p,p} - \mathit{\boldsymbol{X}}_n^{p,p}} \right)} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{X}}_{n + 1}^{p,p} - \mathit{\boldsymbol{X}}_n^{p,p}} \right){\rm{d}}\tau \\ = \int\limits_0^1 \nabla C{\left( {\mathit{\boldsymbol{X}}_n^{p,p} + \tau \left( {\mathit{\boldsymbol{X}}_{n + 1}^{p,p} - \mathit{\boldsymbol{X}}_n^{p,p}} \right)} \right)^{\rm{T}}}\mathit{\boldsymbol{B \boldsymbol{\varTheta} }}_n^{p,p}{\rm{d}}\tau \\ = 0, \end{array} $ |
where the last step is due to the fact that C(X) is a Casimir function such that
In this section, we illustrate the performance of the (p, p) -schemes (13) (l=m=p) via numerical tests. We consider the following linear stochastic Poisson system
| $ \begin{array}{l} {\rm{d}}\mathit{\boldsymbol{X}}(t) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{c}} 0&1&{ - 1}\\ { - 1}&0&3\\ 1&{ - 3}&0 \end{array}} \right) \cdot \left[ {\left( {\begin{array}{*{20}{c}} 2&1&1\\ 1&1&0\\ 1&0&1 \end{array}} \right)\mathit{\boldsymbol{X}}{\rm{d}}t + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\frac{1}{4}\left( {\begin{array}{*{20}{c}} {11}&4&4\\ 4&2&1\\ 4&1&2 \end{array}} \right)\mathit{\boldsymbol{X}} \circ {\rm{d}}W(t)} \right],\\ \mathit{\boldsymbol{X}}\left( {{t_0}} \right) = \mathit{\boldsymbol{x}}. \end{array} $ | (41) |
It can be proved that, the function C(X)=3X(1)+X(2)+X(3) is a Casimir function of the system (41). Moreover, the Hamiltonian functions
| $ H^{1}(\boldsymbol{X})=\left(\boldsymbol{X}^{(1)}+\boldsymbol{X}^{(2)}\right)^{2}+\left(\boldsymbol{X}^{(1)}+\boldsymbol{X}^{(3)}\right)^{2} , $ |
| $ \begin{array}{c} H^{2}(\boldsymbol{X})=11\left(\boldsymbol{X}^{(1)}\right)^{2}+2\left(\boldsymbol{X}^{(2)}\right)^{2}+2\left(\boldsymbol{X}^{(3)}\right)^{2}+ \\ 8 \boldsymbol{X}^{(1)} \boldsymbol{X}^{(2)}+2 \boldsymbol{X}^{(2)} \boldsymbol{X}^{(3)}+8 \boldsymbol{X}^{(3)} \boldsymbol{X}^{(1)} \end{array} $ |
are invariants of the system (41), since it holds
The stochastic poisson integrators, i.e., the (p, p) -schemes (13) (p=1, 2, 3) for (41) read
| $ \boldsymbol{X}_{n+1}^{1,1}=\left(\boldsymbol{I}_{3}+\frac{1}{2} \overline{\boldsymbol{Z}}_{n}\right) \boldsymbol{X}_{n}^{1,1}+\frac{1}{2} \overline{\boldsymbol{Z}}_{n} \boldsymbol{X}_{n+1}^{1,1}, $ | (42) |
| $ \begin{aligned} \boldsymbol{X}_{n+1}^{2,2}=&\left(\boldsymbol{I}_{3}+\frac{1}{2} \overline{\boldsymbol{Z}}_{n}+\frac{1}{12}\left(\overline{\boldsymbol{Z}}_{n}\right)^{2}\right) \boldsymbol{X}_{n}^{2,2}+\\ &\left(\frac{1}{2} \overline{\boldsymbol{Z}}_{n}-\frac{1}{12}\left(\overline{\boldsymbol{Z}}_{n}\right)^{2}\right) \boldsymbol{X}_{n+1}^{2,2}, \end{aligned} $ | (43) |
| $ \begin{aligned} \boldsymbol{X}_{n+1}^{3,3}=&\left(\boldsymbol{I}_{3}+\frac{1}{2} \overline{\boldsymbol{Z}}_{n}+\frac{1}{10}\left(\overline{\boldsymbol{Z}}_{n}\right)^{2}+\frac{1}{120}\left(\overline{\boldsymbol{Z}}_{n}\right)^{3}\right) \boldsymbol{X}_{n}^{3,3}+\\ &\left(\frac{1}{2} \overline{\boldsymbol{Z}}_{n}-\frac{1}{10}\left(\overline{\boldsymbol{Z}}_{n}\right)^{2}+\frac{1}{120}\left(\overline{\boldsymbol{Z}}_{n}\right)^{3}\right) \boldsymbol{X}_{n+1}^{3,3}, \end{aligned} $ | (44) |
where
| $ {\mathit{\boldsymbol{A}}^0}{\rm{ }} = \left( {\begin{array}{*{20}{c}} 0&1&{ - 1}\\ { - 1}&0&3\\ 1&{ - 3}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 2&1&1\\ 1&1&0\\ 1&0&1 \end{array}} \right), $ |
| $ {\mathit{\boldsymbol{A}}^1}{\rm{ }} = \frac{1}{4}\left( {\begin{array}{*{20}{c}} 0&1&{ - 1}\\ { - 1}&0&3\\ 1&{ - 3}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {11}&4&4\\ 4&2&1\\ 4&1&2 \end{array}} \right), $ |
| $ \overline {{\mathit{\boldsymbol{Z}}_n}} = h{\mathit{\boldsymbol{A}}^0} + \sqrt h \zeta _{n,h}^1{\mathit{\boldsymbol{A}}^1}, $ |
with
Figure 1 illustrates the root mean-square orders of the (p, p) -schemes (42), (43) and (44), which are 1, 2 and 3, respectively, coinciding with the theoretical result in Theorem 2.1. Here we take T=10, initial value x=[1, 0, -1], and time steps h=[0.005, 0.01, 0.02, 0.025, 0.05]. The expectation is approximated by taking average over 1 000 sample paths.
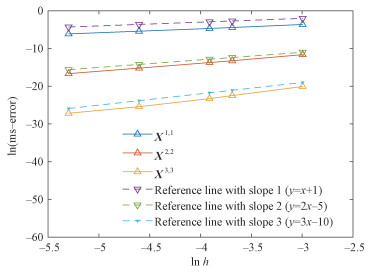
|
Download:
|
|
Fig. 1 Root mean-square convergence orders of (42), (43), and (44) |
|
Figure 2 compares the numerical sample paths of X(1)(t), X(2)(t) and X(3)(t) arising from the (1, 1)-scheme (42) and the implicit Euler method with the reference solution. As can be seen, as time step h=0.01, both numerical methods can create good path approximations. As h=0.1, however, the implicit Euler fails to simulate the paths in acceptable accuracy, while our (1, 1)-scheme (42) still behaves fairly well.
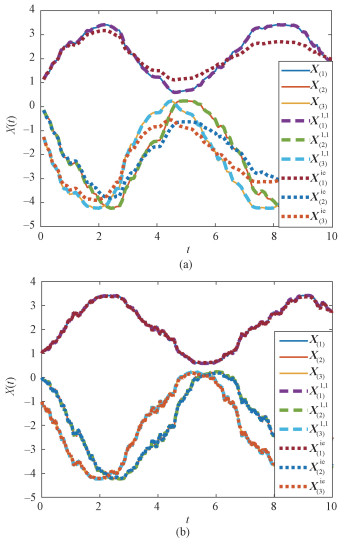
|
Download:
|
|
Fig. 2 Sample paths produced by (42) and the implicit Euler method for h=0.1 (a) and h=0.01(b) |
|
Figure 3 displays the computed Casimir function

|
Download:
|
|
Fig. 3 Preservation of Casimir function by (42), (43), (44), and the implicit Euler method |
|
Figure 4 observes the evolution of the Hamiltonians H1(X(t)) and H2(X(t)) over the time interval t∈[0, 10], produced by the (1, 1)-scheme (42) and the implicit Euler with initial x=[1, 1, 1], by the (2, 2)-scheme (43) with initial x=[1, 1, 2] and by the (3, 3)-scheme (44) with initial x=[1, 1, 3]. It is clear that, the implicit Euler can not preserve the Hamiltonians, while our (p, p) -schemes (p=1, 2, 3) can. Here we take h=0.1.
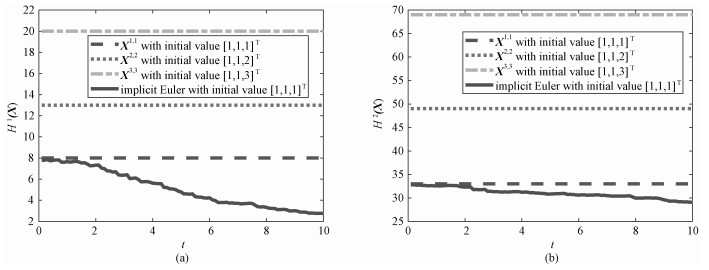
|
Download:
|
|
Fig. 4 Evolutions of H1 (a) and H2 (b) by (42), (43), (44), and the implicit Euler method |
|
Figure 5 demonstrates the evolution of the relative error
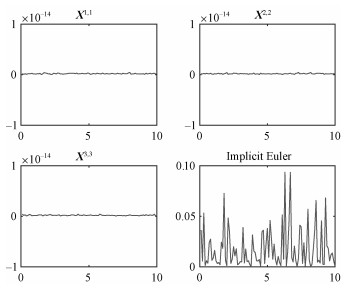
|
Download:
|
|
Fig. 5 Error evolutions of the Poisson structure by (42), (43), (44), and the implicit Euler method |
|
Theoretical and empirical analyses show that the (p, p) -schemes, based on the Padé approximations, can simulate the linear stochastic Poisson systems with arbitrarily high root mean-square orders
| [1] |
Hong J L, Ruan J L, Sun L Y, et al. Structure-preserving numerical methods for stochastic Poisson systems[J]. Communications in Computational Physics, 2021, 29(3): 802-830. DOI:10.4208/cicp.OA-2019-0084 |
| [2] |
Milstein G N, Repin Y M, Tretyakov M V. Symplectic integration of Hamiltonian systems with additive noise[J]. SIAM Journal on Numerical Analysis, 2002, 39(6): 2066-2088. DOI:10.1137/S0036142901387440 |
| [3] |
Milstein G N, Repin Y M, Tretyakov M V. Numerical methods for stochastic systems preserving symplectic structure[J]. SIAM Journal on Numerical Analysis, 2002, 40(4): 1583-1604. DOI:10.1137/S0036142901395588 |
| [4] |
Ruan J L, Wang L J. A Lie algebraic approach for a class of highly oscillatory stochastic Hamiltonian systems[J]. Journal of University of Chinese Academy of Sciences, 2019, 36(1): 5-10. |
| [5] |
Feng K, Qin M Z. Symplectic geometric algorithms for Hamiltonian systems[M]. Berlin: Springer Science & Business Media, 2010.
|
| [6] |
Hairer E, Lubich C, Wanner G. Geometric numerical integration[M]. Berlin: Springer Science & Business Media, 2006.
|
| [7] |
Zhu W J, Qin M Z. Poisson schemes for Hamiltonian systems on Poisson manifolds[J]. Computers & Mathematics with Applications, 1994, 27(12): 7-16. |
| [8] |
Cohen D, Dujardin G. Energy-preserving integrators for stochastic Poisson systems[J]. Communications in Mathematical Sciences, 2014, 12(8): 1523-1539. DOI:10.4310/CMS.2014.v12.n8.a7 |
| [9] |
Hong J L, Ji L H, Wang X. Stochastic K-symplectic integrators for stochastic non-canonical Hamiltonian systems and applications to the Lotka-Volterra model[EB/OL]. arXiv: 1711.03258v1[math. NA] (2017-11-09)[2019-07-02]. https://arxiv.org/abs/1711.03258.
|
| [10] |
Feng K, Wu H M, Qin M Z. Symplectic difference schemes for linear Hamiltonian canonical systems[J]. Journal of Computational Mathematics, 1990, 8(4): 371-380. |
| [11] |
Sun L Y, Wang L J. Stochastic symplectic methods based on the Padé approximations for linear stochastic Hamiltonian systems[J]. Journal of Computational and Applied Mathematics, 2017, 311: 439-456. DOI:10.1016/j.cam.2016.08.011 |
| [12] |
Aboanber A E, Nahla A A. On Padé approximations to the exponential function and application to the point kinetics equations[J]. Progress in Nuclear Energy, 2004, 44(4): 347-368. DOI:10.1016/j.pnucene.2004.07.003 |
| [13] |
Milstein G N. Numerical integration of stochastic differential equations[M]. Berlin: Springer Science & Business Media, 1995.
|
 2021, Vol. 38
2021, Vol. 38 


