2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
从基础物理学可以得知,电磁波除携带线动量,也携带角动量[1]。角动量由两个部分组成:一是自旋角动量SAM(spin angular momentum), 与电磁波的极化状态有关;二是轨道角动量OAM(orbital angular momentum),与电磁波幅度及相位在空间分布有关。
近年来,将OAM应用于无线通信系统引起了极大的关注。其中至关重要的一个原因是在理论上OAM有无穷多个本征态,且不同模态之间相互正交,即OAM这种性质在功能上类似于大规模MIMO天线,提供了一种全新的自由度。因而在现有无线通信技术的基础上,利用携带OAM的涡旋电磁波作为信息传输过程中的载体可以极大提高通信系统容量,提升频谱利用率[2-5]。最初在光学领域中研究OAM特性, 并获得了很多应用[6-7];随后有学者提出OAM也能够应用于低频当中[8]。如今有很多方法能够产生携带OAM的涡旋电磁波,有螺旋相位板[9]、时间开关阵列[10]等。同向均匀圆环阵列天线是一个比较常见的用于产生携带OAM的涡旋电磁波方法,文献[11-18]验证了该方法的可行性,通过给每个阵元馈入等幅度,相邻阵元等相差的激励信号即可产生携带OAM的涡旋电磁波;文献[19-24]提出径向、切向均匀圆环阵列天线可以产生携带OAM的涡旋电磁波并验证成功。其中文献[19]采用8个单元的Vivaldi天线,通过给每个天线阵元馈入等幅度,相邻阵元等相差的激励信号,并依次改变相位差值,分别研究径向均匀圆环阵所产生的模态值为±1、±2、±3等几种情况下的涡旋电磁波,发现在模态值为±1时并不存在方向图零陷,具体原因文献[21]给出了说明;文献[22]采用12个天线单元分别研究同向、径向、切向3种结构的圆环阵列产生的涡旋电磁波,结果表明在模态值为+1时,同向阵存在方向图零陷,径向、切向阵却没有。文献[25-27]利用波束同轴产生并发射的原理形成了携OAM双模复用的涡旋电磁波。
本文基于均匀圆环阵列,对其所产生的携OAM双模复用的涡旋电磁波进行研究。首先从理论上论述均匀圆环阵列可以产生携带OAM涡旋电磁波,并提出3种不同结构的均匀圆环阵列、阵元的激励设置及传输增益的计算方法;其次选取径向均匀圆环阵列从阵元的数量、阵列的半径及阵元的排列方式3个角度分别讨论了其对所产生的携OAM双模复用的涡旋电磁波在主轴方向上远场增益的影响;最后从阵元的排列方式研究OAM双模复用时的模间干扰程度。
1 理论模型一个典型的均匀圆环阵列结构图如图 1所示, 假设有N个阵元均匀分布在半径为a的圆环上,则该圆环阵列在远场区所产生的总电磁场强度[21]为
| $ {E_n}(r,\theta ,\varphi ) = \sum\limits_{n = 1}^N {{x_n}} \frac{{{{\rm{e}}^{ - {\rm{j}}k{R_n}}}}}{{{R_n}}}, $ | (1) |

|
Download:
|
| 图 1 均匀圆环阵列结构图 Fig. 1 Uniform circular array structure | |
其中:xn为阵元的激励信号,k为波尔茨曼常数,Rn为观测点到阵元的距离。当r≫a时,有
| $ {R_n} \approx r - a\sin \theta \cos \left( {\varphi - {\varphi _n}} \right). $ | (2) |
假设Rn=r,可以得到如下的整个电磁场强度表达形式
| $ {E_n} = \frac{{{{\rm{e}}^{ - {\rm{j}}kr}}}}{r}\sum\limits_{n = 1}^N {{x_n}} {{\rm{e}}^{{\rm{j}}ka\sin \theta \cos \left( {\varphi - {\varphi _n}} \right)}}. $ | (3) |
通过给均匀圆环阵列中的每一个阵元馈入激励信号,令
| $ {x_n} = {I_0}\exp ({\rm{j}}l\phi ), $ | (4) |
其中:I0为幅度,ϕ为激励信号的相位,ϕ=ϕn-1+2πnl/N,l为OAM的模态值,N为均匀圆环阵列中所有阵元总数。将式(4)代入式(3)可得到
| $ {E_n} = \frac{{{{\rm{e}}^{ - {\rm{j}}kr}}}}{r}\sum\limits_{n = 1}^N {{I_0}} {{\rm{e}}^{{\rm{j}}\left( {ka\sin \theta \cos \left( {\varphi - {\varphi _n}} \right) + l\phi } \right)}}. $ | (5) |
由式(5)可知该均匀圆环阵列在远场区所产生的电磁场相位分布含有ejlϕ,这表明所产生的电磁波携带OAM,沿着传播方向具有螺旋形相位波前的特点。
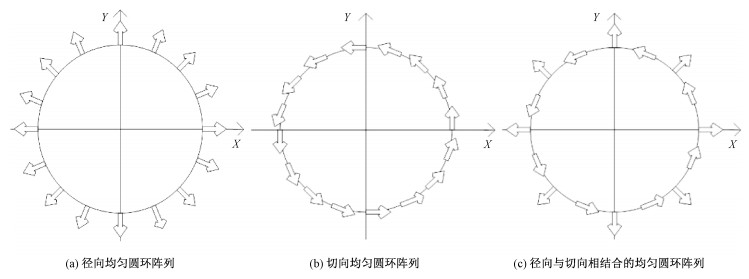
2 圆环阵列结构、激励设置及传输增益的计算 2.1 圆环阵列结构 2.1.1 径向均匀圆环阵列径向均匀圆环阵列平面结构如图 2(a)所示,箭头的指向为天线的极化方向。由于每个阵元都按照径向排列而导致初始电场矢量方向(天线极化方向)呈现出均沿所在圆环半径全部背向或全部面向圆心的阵列排布形式。该圆环阵列共含有16个偶极子天线单元,将其看成是由两组8单元径向均匀圆环阵列结构组成,同轴同半径,且各个天线单元之间的间隔相等。
|
Download:
|
| 图 2 3种不同结构的均匀圆环阵列结构图 Fig. 2 Uniform circular array structure diagram of three different structures | |
切向均匀圆环阵列平面结构如图 2(b)所示,箭头的指向为天线的极化方向。由于每个阵列单元都按照切向排列而导致初始电场矢量方向(天线极化方向)呈现出均沿所在圆环的切线方向全部顺时针或者逆时针排布形式。该圆环阵列共含有16个偶极子天线单元,将其看成是由两组8单元切向均匀圆环阵列结构组成,同轴同半径,且各个天线单元之间的间隔相等。
2.1.3 径向与切向相结合的均匀圆环阵列径向与切向相结合的均匀圆环阵列平面结构如图 2(c)所示,箭头的指向为天线的极化方向。该圆环阵列共含有16个偶极子天线单元,将其看成是由一组8单元径向均匀圆环阵列和一组8单元切向均匀圆环阵列相结合而构成,同轴同半径,且各个天线单元之间的间隔相等。
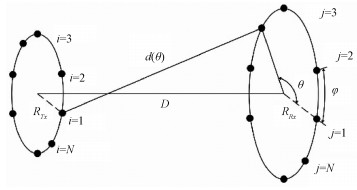
2.2 激励设置及传输增益计算为了发射并接收携带OAM的涡旋电磁波,给出如图 3所示的发射-接收示意图,轴心直线距离为D, 发射端任意一个天线阵元到接收端任意一个天线阵元的直线距离为d(θ), 圆环半径分别为RTx、RRx,发射端和接收端各有NTx、NRx个天线单元(NTx=NRx=N),均匀分布在圆环阵列上。根据电磁场理论可以求出理想条件下该传输模型从发射端到接收端整体的传输系数矩阵[13]为
| $ \mathit{\boldsymbol{H}} = \left( {\begin{array}{*{20}{c}} {{s_{1,1}}}& \cdots &{{s_{{N_{Tx}},1}}}\\ \vdots &{}& \vdots \\ {{s_{1,{N_{Rx}}}}}& \cdots &{{s_{{N_{Tx}},{N_{Rx}}}}} \end{array}} \right), $ | (6) |
| $ {S_{{N_{Tx,}}{N_{Rx}}}} = \beta \frac{\lambda }{{4{\rm{ \mathsf{ π} }}{d_{{N_{Tx,}}{N_{Rx}}(\theta )}}}}\exp \left( { - {\rm{j}}2{\rm{ \mathsf{ π} }}\frac{{{d_{{N_{Tx,}}{N_{Rx}}}}(\theta )}}{\lambda }} \right). $ | (7) |
|
Download:
|
| 图 3 均匀圆环阵列收发示意图 Fig. 3 Uniform ring array transmission and reception diagram | |
其中:SNTx, NRx为发射端口NTx到接收端口NRx的传输系数,β为衰减因子,λ为波长。
现假设有两个分别携带不同OAM模态值的涡旋电磁波共轴复用传输,将发射端含NTx个天线单元的均匀圆环阵列看成是由A、B两组各含NTx/2个天线单元的均匀圆环阵列所构成;接收端也同理,将接收端含NRx个天线单元的均匀圆环阵列看成是由C、D两组各含NRx/2个天线单元的均匀圆环阵列所构成。A组均匀圆环阵列发射携OAM模态值为l1的涡旋电磁波,B组均匀圆环阵列发射携OAM模态值为l2的涡旋电磁波,C组均匀圆环阵列用于接收由A组均匀圆环阵列发射的涡旋电磁波,D组均匀圆环阵列用于接收由B组均匀圆环阵列发射的涡旋电磁波。但是因为电磁波及天线的特性,A组均匀圆环阵列天线发射的涡旋电磁波除C组天线可以接收外,D组天线也可以接收到,所以将A、C之间的传输增益视为同模间的传输增益,A、D之间的传输增益视为异模间的传输增益。
当发射端A组均匀圆环阵列要发送模态值为l1、幅度值为Il1的OAM,对于发射端NTx/2个天线单元,任意一个天线单元被馈入的信号[14]为
| $ x_n^{{\rm{feed}}} = \frac{{{I_{{l_1}}}}}{{\sqrt {{N_{Tx}}/2} }}\exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}\frac{{n{l_1}}}{{{N_{Tx}}/2}}} \right),n \in 1, \cdots ,{N_{Tx}}/2, $ | (8) |
则发射端A所有的激励信号组合成一个矩阵U,其中U=[x1, …, xn]T。此时C组均匀圆环阵列要接收由发射端A所产生的OAM,接收端C组均匀圆环阵列中任意一个天线单元被馈入的信号为
| $ \begin{array}{*{20}{c}} {y_n^{{\rm{received }}} = \frac{{{I_{{l_1}}}}}{{\sqrt {{N_{Rx}}/2} }}\exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}\frac{{n\left( { - {l_1}} \right)}}{{{N_{Rx}}/2}}} \right),}\\ {n \in 1, \cdots ,{N_{Rx}}/2,} \end{array} $ | (9) |
则接收端C所有的激励信号组合成一个矩阵V,V=[y1, …, yn];同理可分别求出发射端B组中所有阵元的激励信号组成的矩阵U′,接收端D组中所有阵元的激励信号组成的矩阵V′。分别求出A、C之间的传输系数矩阵H,A、D组之间的传输系数矩阵H′,从而可求出同模之间的传输增益W, 异模之间的传输增益W′。
| $ {\mathit{\boldsymbol{W}} = \mathit{\boldsymbol{V}} * (\mathit{\boldsymbol{H}} * \mathit{\boldsymbol{U}}),} $ | (10) |
| $ {{\mathit{\boldsymbol{W}}^\prime } = {\mathit{\boldsymbol{V}}^\prime } * \left( {{\mathit{\boldsymbol{H}}^\prime } * {\mathit{\boldsymbol{U}}^\prime }} \right).} $ | (11) |
本节主要从均匀圆环阵列中阵元的数量、阵列的半径及阵元的排列方式3个角度分别讨论其对所产生的携OAM双模复用的涡旋电磁波远场增益的影响,并选取5.8 GHz为中心频点。对于本节讨论所需的径向阵与切向阵通过4NEC软件仿真得出其螺旋相位波前如图 4所示,从而可以说明OAM的产生。

|
Download:
|
| 图 4 径、切圆环阵螺旋相位波前图 Fig. 4 Helical phase wavefronts of the radial, tangential array | |
由文献[25]可知,在均匀圆环阵列中,阵元的数量决定了该均匀圆环阵列所能产生的OAM模态值-N/2 < l < N/2,其中N为均匀圆环阵列中阵元的总数,如果模态值l不在该区间内,则无法产生一个稳定的OAM,携带该模态值OAM的涡旋电磁波则会变得扭曲,本文中所产生的模态值为+1、-1,且N大于4,所以均处在以上区间范围内。
本小节采用如图 2(a)所示的径向均匀圆环阵列并利用4NEC软件进行仿真,根据2.2节提到的激励设置规则,对每一个阵元设置相应的相位与幅度,从而能够生成-1、+1双模复用的OAM。通过改变阵元的数量,圆环阵列半径与阵元的排列方式均保持不变,一一验证,给出当阵元数量为16、12、8这3种情况时的远场增益图,如图 5(a)、5(b)、5(c),从图中可以看出,主轴上的增益值分别为13.7、11.7和10.5 dB,由此可得阵元的数量对OAM双模复用的远场增益影响较大,阵元数量越多,主轴上的远场增益越大。

|
Download:
|
| 图 5 径向阵阵元的数量与主轴远场增益的关系 Fig. 5 Relationship between the number of array elements and spindle gain | |
本小节依旧采用如图 2(a)所示的径向均匀圆环阵列并利用4NEC软件进行仿真,通过维持阵元数量及其排列方式不变,依次改变圆环阵列半径为λ、2λ、3λ (λ为波长),得到如图 6(a)、6(b)、6(c)所示的增益图。从图中可以看出,主轴上的增益值分别为13.7、12.9和12.9 dB, 由此可得半径对主轴上的远场增益影响不大。

|
Download:
|
| 图 6 径向阵阵列半径与主轴远场增益的关系 Fig. 6 Relationship between the array radius and spindle gain | |
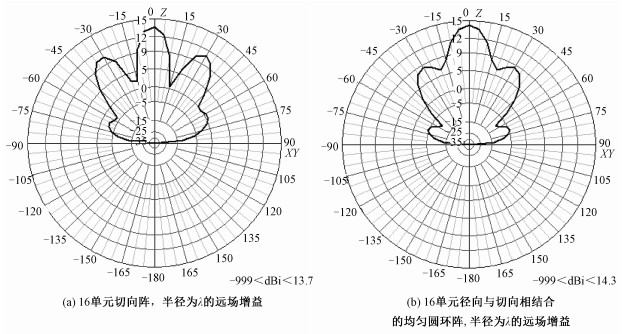
本小节采用如图 2(b)、2(c)所示的切向均匀圆环阵列及径向与切向相结合的均匀圆环阵列,通过维持圆环阵列半径及阵元数量与图 5(a)中的径向阵一样,仅改变排列方式,利用4NEC软件进行仿真得到如图 7(a)、7(b)所示的增益图。从图中可以看出,切向阵其主轴上的远场增益为13.7 dB,与径向阵相同,而径向与切向相结合的均匀圆环阵其主轴上的远场增益为14.3 dB, 即该结构的远场增益较高。
|
Download:
|
| 图 7 阵元的排列方式与主轴远场增益的关系 Fig. 7 Relationship between the array structure and spindle gain | |
通过如图 3所示的发射-接收示意图对携带OAM的涡旋电磁波进行发射与接收,现设定轴心直线距离为D=900 mm, 发射端任意一个天线阵元到接收端任意一个天线阵元的直线距离为d(θ), 圆环半径分别为RTx、RRx(RTx=RRx=λ, 其中λ为波长),发射端和接收端各有NTx、NRx个天线单元(NTx=NRx=16),均匀分布在圆环阵列上,并依据2.2节中提到的激励设置方法,依次给每一个阵元馈入信号。
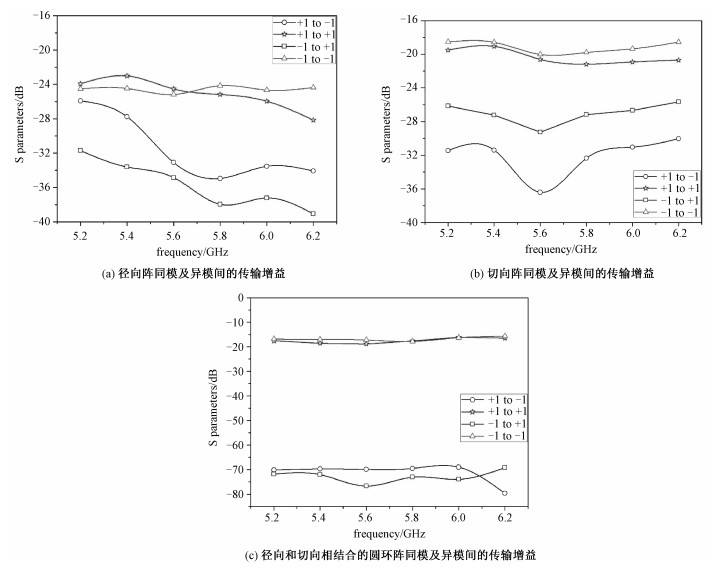
通过HFSS仿真分别得到径向均匀圆环阵列、切向均匀圆环阵列以及径向和切向相结合的均匀圆环阵列在频率为5.2~6.2 GHz区间下的同模与异模之间传输增益结果,如图 8(a)、8(b)、8(c)所示。取中心频点5.8 GHz处的值,得到表 1。其中-1 to -1和+1 to +1代表同模之间的传输增益,-1 to +1和+1 to -1代表异模之间的传输增益,同模之间的传输增益减去异模之间的传输增益即为模间隔离度。理论上两种情况下同模之间的传输增益应该相等,同理两种情况下异模之间的传输增益也相等。但由于仿真软件自身存在一定的计算精度误差以及各天线单元之间存在一定的耦合,所以导致实际仿真出的结果和理论有少许的不一致。由表 1可知,在以上3种结构下产生的携OAM双模复用的涡旋电磁波,其最小隔离度平均值分别为10、11和53 dB。从而可知相对于径向均匀圆环阵列和切向均匀圆环阵列,由径向和切向相结合的均匀圆环阵列产生的携OAM双模复用的涡旋电磁波,其模间隔离度更大。
|
Download:
|
| 图 8 3种不同结构的圆环阵列产生的OAM双模复用时传输增益 Fig. 8 OAM dual-mode multiplexing transmission gain generated by three different arrays of circular arrays | |
|
|
表 1 3种不同结构的圆环阵列产生的OAM双模复用时传输增益(5.8 GHz) Table 1 OAM dual-mode multiplexing transmission gain generated by three different arrays of circular arrays(5.8 GHz) |
本文基于均匀圆环阵列,对其所产生的携OAM双模复用的涡旋电磁波进行研究。实验仿真得出的结果表明,在均匀圆环阵列中阵元数量对主轴上的远场增益影响较大,主要表现为阵元数量越多,主轴上的增益越高;圆环阵列半径对主轴上的远场增益影响较小;阵元的排列方式除对主轴上的远场增益影响较大以外,对模间干扰程度也有很大影响,主要表现为对于使用一种排列方式形成的均匀圆环阵列天线而言,采用两种不同排列方式组合而成的均匀圆环阵列所产生携OAM双模复用的涡旋电磁波不仅在主轴方向上增益更大,而且模间干扰小, 从而可以提供更加可靠的信息传输。
本论文只从均匀圆环阵列中阵元的数量、阵列半径以及阵元的排列方式3个角度研究了其所产生的携OAM双模复用的涡旋电磁波,还有很多其他因素有待进一步研究。
| [1] |
Poynting J. The wave motion of a revolving shaft, and a suggestion as to the angular momentum in a beam of circularly polarised light[J]. ProcR Soc Lond A, 1909, 82(557): 560-567. |
| [2] |
Nguyen T, Hirabe M, Miyamoto H, et al. An ex-perimental study of high capacity link using orbital angular momentum mode multiplexing in E-band[J]. International Symposium on Antennas and Propagation, 2018, 12: 1-2. |
| [3] |
Yan Y, Li L, Zhao Z, et al. 32-Gbit/s 60-GHz millimeter-wave wireless communication using orbital angular momentum and polarization multiplexing[J]. Proc IEEE ICC, 2016, 104: 1-6. |
| [4] |
Tamburini F, Mari E, Sponselli A, et al. Encoding many channels on the same frequency through radio vorticity:first experimental test[J]. New J Phys, 2012, 14(3): 78001-78004. |
| [5] |
Shu G, Wang W, Liang D, et al. Chirp signal transmission and reception with orbital angular momentum multiplexi[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(5): 986-990. |
| [6] |
Allen L, Beijersbergen G, Spreeuw H, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Phys Rev A, 1992, 45(11): 8185-8189. Doi:10.1103/PhysRevA.45.8185 |
| [7] |
Lavery M, Robertson P. Efficient measurement of an optical orbital angular momentum spectrum comprising more than 50 states[J]. New J Phys, 2013, 15: 1354-1357. |
| [8] |
Thidé B, Istomin Y N, Khamitova R, et al. Utilization of photon orbital angular momentum in the low-frequency radio domain[J]. Phys Rev Lett, 2007, 99(8): 087701. Doi:10.1103/PhysRevLett.99.087701 |
| [9] |
Hui X, Zheng S, Hu Y, et al. Ultralow reflectivity spiral phase plate for generationof millimeter-wave OAM beam[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14(1): 966-969. |
| [10] |
Tennant A, Allen B. Generation of OAM radio waves using circular time-switched array antenna[J]. Electron Letters, 2012, 48(21): 1365-1366. |
| [11] |
Liu Q, Chen Z N, Liu Y A, et al. Circular polarization and mode reconfig-urable wideband orbital angular momentum patch arrayantenna[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(12): 7010-7020. |
| [12] |
Gong Y, Wang R, Deng Y, et al. Generation and transmission of OAM carrying vortex beams using circular antenna array[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(6): 2940-2949. |
| [13] |
Edfors O, Johansson A J. Is orbital angular momentum (OAM) based radio communication an unexploited area?[J]. IEEE Transaction on Antennas and Propagation, 2012, 60(2): 1126-1131. |
| [14] |
Bai Q, Tennant A, Allen B. Experimental circular phased array for ge-nerating OAM radio beams[J]. Electron Lett, 2014, 50(20): 1414-1415. |
| [15] |
Tan S, Dong J, Wang M, et al. New circular array configurations for generating orbital angular momentum(OAM) beams[J]. International Applied Computational Electromagnetics Society Symposium, 2018, 67: 1-2. |
| [16] |
Lin M, Gao Y, Liu P, et al. Theoretical analyses and design of cir-cular array to generate orbital angular momentum[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(7): 10-19. |
| [17] |
Yuan T, Wang H, Cheng Y. Electromagnetic vortexbased radar imaging using a single receiving antenna:theory and experimental results[J]. Sensor, 2017, 17(3): 630-635. |
| [18] |
Mohammadi S M, Daldorff L K S, Bergman E S, et al. Orbital angular momentum in radio:a system study[J]. IEEE Transactions on Antennas and Propagation, 2010, 58: 565-572. Doi:10.1109/TAP.2009.2037701 |
| [19] |
Deng C, Chen W, Feng Z. Generation of OAM radio waves using circular vivaldi antenna array[J]. Int J Antennas Propagation, 2013, 17: 90-97. |
| [20] |
Zhang Y, Li J. radial uniform circular antenna array for dual-mode OAM communication[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(4): 719-721. |
| [21] |
Guo Z, Yang G. Radial uniform circular antenna array for dual-mode OAM communication[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 404-407. |
| [22] |
Wu H, Yuan Y, Zhang Z, et al. UCA-based orbital angular moment-um radio beam generation and reception under differe-nt array configurations[C]//6th International Conference on Wireless Communications and Signal Processing (WCSP), 2014: 1-6.
|
| [23] |
Zheng S, Hui X, Jin X, et al. Transmission characteristics of a twisted radio wave based on circular traveling wave antenna[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(4): 1530-1536. |
| [24] |
Guo C, Zhao X, Zhu C, et al. An OAM patch antenna design and its array for higher order OAM mode generation[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(5): 816-820. Doi:10.1109/LAWP.2019.2900265 |
| [25] |
Spinello F, Someda C G, Ravanelli R A, et al. Radio channel multiplexing with superpositions of opposite sign OAM modes[J]. AEU-International Journal of Electronics and Communications, 2016, 70(8): 990-997. Doi:10.1016/j.aeue.2016.03.017 |
| [26] |
Hui X, Zheng S, Chen Y, et al. Multiplexed millimeter wave communication with dual orbital angular momentum (OAM) mode antennas[J]. Scientific Reports, 2015, 5: 10148. |
 2021, Vol. 38
2021, Vol. 38 


