2. 中国科学院大学, 北京 100049;
3. 北京自动化工程学校, 北京 100101
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Beijing Automatic Engineering School, Beijing 100101, China
可靠性验证试验(reliability demonstration test, RDT)通过数理统计的方法验证产品失效率、平均故障间隔时间(mean time to failure, MTBF)等寿命、可靠性参数是否达到规定要求,其目的在于使订购方拿到合格的产品,同时承制方也能了解产品的寿命与可靠性[1],一般采用真实应力条件,其试验时间主要取决于待验证的可靠性水平和选用的统计试验方案,在GJB899A-2009“可靠性鉴定与验收试验”中给出了各类可靠性验证试验统计试验方案[2]。在航空航天领域等大多数工程应用场合,系统级产品通常逐一采用典型温度、振动等单项环境试验替代实际综合应力可靠性试验,开展鉴定、验收试验,对产品指标进行保守验证,得出“通过与否”的定性结论,仅对关键重要的寿命敏感部组件开展寿命评估试验。
为了节约时间与成本,通常采用“数理统计+故障物理”的可靠性加速验证试验(reliability accelerated demonstration test, RADT)方法,在失效机理不变的前提下增加应力水平,在短时间内获得更多试验数据,基于加速数据对正常条件下产品的可靠性指标进行评估验证。国内外学者对RADT方案设计的研究按数据类型主要分为基于寿命数据和基于退化数据两类。
在基于寿命数据(失效数和失效时间)的加速验证试验方面,Guo和Liao[3]从理论和应用两方面阐释基于失效数和基于失效时间的两类可靠性验证方法;Yadav等[4]按严酷度等级将系统可靠度分解,对特定失效机理及物理单元开展可靠性验证试验;Li等[5]针对多失效模式产品,将可靠性指标分解至各环境应力,建立综合加速模型,提出系统多应力加速验证试验方法,并给出试验剖面;Xu等[6]分别对服从指数分布和威布尔分布的两类负载均衡系统提出验证方法;Chen等[7]提出一套加速试验剖面建立方法,考虑多失效机理推导出理论寿命模型;Chen等[8]为克服传统0-1失效的二态可靠性验证试验缺陷,针对多时段、多失效模式的可靠性指标验证问题提出多态可靠性验证试验方法;Kleyner[9]讨论现场应力变化对所验证的可靠性指标的影响,指出应力的不确定性会给验证试验结果带来极大的误差;Xu等[10]研究可靠性增长情况下的可靠性验证试验,提出基于幂律增长模型的可靠性验证优化新模型。
在基于性能退化的加速验证试验方面,Chang等[11]比较分析采用基于退化和基于零失效的气缸可靠性鉴定试验,得到基于性能退化数据的验证方法可缩短试验时间,节省试验样本的结论;Xu等[12]提出一种故障物理结合统计分析的建模方法,利用自适应卡尔曼滤波方法对可靠性和寿命进行验证;Jin和Matthews[13]针对长寿命产品样本量不足的问题,提出基于Wiener过程的验证试验方法,分析比较固定样本、序贯概率比试验,以及序贯贝叶斯决策的优劣,建立基于加速退化模型的验证试验优化方法;Luo等[14-15]提出基于可靠性分配的竞争失效场合加速验证方法,以及模型参数未知时基于加速退化试验的可靠性验证试验方法;Zhang等[16]基于Gamma退化过程提出RADT方法,推导严酷应力下等效可靠性指标,建立费用约束下的应力水平、样本大小、平均失效时间的优化方案。
现有的RADT设计理论和方法正在逐渐丰富和完善中,但一方面难以获取足量失效数据或性能监测数据,另一方面复杂系统存在失效机理、模型未知、多应力耦合失效等难题。在工程应用场合,IEC62506产品加速试验方法采用等分配法将可靠性指标均等分配给各环境应力,再采用加速应力来验证产品可靠性指标。基于此,借鉴可靠性指标按环境应力进行分配的思路,全面分析可靠性影响因素,研究系统可靠性指标分配新方法,将可靠性指标转换为加速应力下的目标可靠性参数,旨在解决多元件多失效模式,多应力类型多量级水平综合加速因子确定方法,以及关联失效模式等难题。
为解决RDT时间长、花费高的问题,快速验证系统可靠性指标,本文提出一种基于模糊层次分析法的系统加速验证试验方法。利用模糊层次分析法将系统任务可靠性指标分配给关键单元所经受的各环境应力;利用加速因子不变原则求得总加速因子,基于应力强度干涉模型和加速模型,设计加速试验剖面,结合统计试验方案,构建RADT方案;最后结合案例分析比较不同设计方法的差异,验证本方法的优越性。
1 系统加速验证试验设计方案系统失效对应映射关系为功能→结构→失效模式/机理→环境应力,如图 1所示,由可靠性框图和故障模式、机理与影响分析对系统可靠性指标按功能、结构、机理、应力4层次分解。通过功能分析推断系统无法正常运行导致的功能失效,对应于参与完成某功能的子系统或部组件,通过失效分析获取致使某单元无法完成规定功能的失效模式机理,对应各环境应力。分析产品可靠性影响因素,对系统失效进行加速试验机理分析和建模,可靠性模型表征各功能、各结构之间的关系;寿命模型刻画寿命特征随时间的变化关系;加速模型描述产品寿命特征与加速应力水平间的物理化学关系。通过分析产品的失效模式、机理及其影响定位导致产品功能障碍的设计薄弱环节,确定主失效机理及其对应的工作、环境应力[17]。

|
Download:
|
| 图 1 系统加速试验机理分析与建模 Fig. 1 Analysis and modeling of system-level accelerated test | |
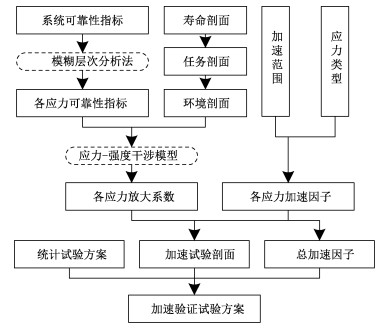
系统加速验证试验方案设计如图 2所示。首先,根据模糊层次分析法将系统可靠性指标按系统单元所经受的各应力进行分配,结合产品环境试验剖面,利用应力强度干涉模型,可得各验证试验中各应力放大系数;然后考虑试验可行性,根据试验设备能力以及由强化试验或历史经验确定的产品应力极限联合确定应力类型和施加范围,计算各应力加速因子,结合放大系数获得产品加速试验剖面;最后,选取合适的验证试验统计方案,结合各应力综合加速因子,可设计得到系统加速验证试验方案。
|
Download:
|
| 图 2 系统加速验证试验方案设计流程 Fig. 2 Procudure of system-level RADT design | |
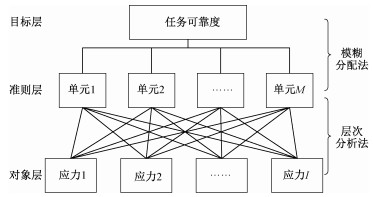
将系统可靠性影响因素自上而下按层次分解,同一层的因素既对上一层有影响,又受到下一层作用。建立如图 3所示的3层次结构模型:目标层对应系统某功能的任务可靠性指标;准则层对应组成系统的各结构单元;对象层对应影响各子系统可靠性的应力。
|
Download:
|
| 图 3 可靠性分配层次结构模型 Fig. 3 Hierarchical structure model for reliability allocation | |
第1步,由模糊分配法得到各单元分配权重ωi。首先确定影响因素,利用梯形模糊数进行模糊量化,采用线性规划法处理梯形模糊除法、质心法去模糊,最后通过多级模糊综合评判法进行分配。第2步,通过三标度层次分析法得到各单元与应力的权重γij[18-20]。因此系统可靠性指标按环境应力类型分配权重为
| $ {\eta _{ij}} = {\omega _i}{\gamma _{ij}}, $ | (1) |
当系统组成为串联结构时,各环境应力对应的可靠度为
| $ {R_{ij}} = {R^{{w_{ij}}}}. $ | (2) |
式中,归一化权重为wij=ηij/∑ηij。
2.1 模糊分配法1) 建立因素集、因素子集和备择集
如表 1所示,综合考虑设计制造、系统属性、使用维护等3类系统可靠性影响因素,构建因素集U={U1, U2, U3},进一步将各因素细分为费用、工艺水平、复杂性、技术难度、工作时间、严酷度、维修度等子因素,因素子集为U1={u11, u12},U2={u21, u22, u23},U3={u31, u32}。根据可靠性分配原则,费用、复杂度、技术难度、维修水平与权重成正比,工艺水平、工作时间、严酷度与权重成反比。
|
|
表 1 因素模糊评价表 Table 1 Fuzzy rating for reliability allocation factors |
因此,各因素比例系数为A1=u11/u12,A2=u21u22/u23,A3=u32/u31。
| $ \left\{ {\begin{array}{*{20}{l}} {{A_1} = {u_{11}}/{u_{12}}}\\ {{A_2} = {u_{21}}{u_{22}}/{u_{23}}}\\ {{A_3} = {u_{32}}/{u_{31}}} \end{array}} \right.. $ | (3) |
对多级模糊评判,备择集元素为各结构单元,可设为S={S1, S2, …,SM},其中M为单元个数。
2) 建立因素评价集和相应分值集
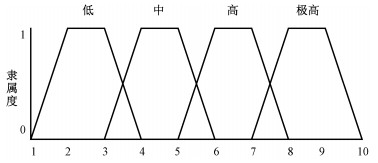
考虑专家评判不确定性,采用梯形模糊数来量化模糊术语,低、中、高、极高等模糊逻辑对应的评价集分别为(7, 8, 9, 10)、(5, 6, 7, 8)、(3, 4, 5, 6)、(1, 2, 3, 4),隶属度函数如图 4所示。
|
Download:
|
| 图 4 因素及隶属度函数的模糊评级 Fig. 4 Fuzzy rating for factor and membership function | |
各评价等级对应着隶属度,即各等级的标准量化值,其取值由各因素对综合评分数的作用效果确定。从低到高4个等级的隶属度组成分值集,可记为V=(v1, v2, v3, v4)=(0.25, 0.5, 0.75, 1)。
3) 确定权重集和权重子集
根据影响程度的差异分别对类因素及其子因素赋予相应的权重值,建立权重集和权重子集。因素权重集为A=[a1, a2, a3],其中ap为第p个类因素的权数,
通过改进梯形模糊数赋权法,避免了主观经验赋值引入的不确定性。模糊集
| $ {\mu _{\tilde U}}(x) = \left\{ {\begin{array}{*{20}{l}} {\frac{{x - a}}{{b - a}},}&{a \le x \le b}\\ {1,}&{c \le x \le d}\\ {\frac{{d - x}}{{d - c}},}&{c \le x \le d}\\ {0,}&{{\rm{其他}}} \end{array}} \right.. $ | (4) |
梯形模糊数的乘法采用矩阵点乘法则,而对于模糊数的除法运算,为减少结果的模糊性,采用基于线性规划的梯形模糊数除法。假设有模糊数
| $ \tilde X = \frac{{\tilde P}}{{\tilde Q}}. $ | (5) |
约束条件如下式所示:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_l} \ge \frac{{{\alpha _1}}}{{{\alpha _2}}} - \frac{{{\alpha _1} - {l_1}}}{{{\alpha _2} - {l_2}}}}\\ {{x_r} \le \frac{{{\beta _1}}}{{{\beta _2}}} + \frac{{{r_1} - {\beta _1}}}{{{r_2} - {\beta _2}}}} \end{array} \cap \left\{ \begin{array}{l} {x_l} < \frac{{{\alpha _1}}}{{{\beta _2}}}\\ {x_r} < \frac{{{\alpha _2}}}{{{\beta _1}}} \end{array} \right.} \right.. $ | (6) |
目标函数可写成
| $ {\mathop{\rm Max}\nolimits} f(x) = {x_r} - {x_l}. $ | (7) |
对梯形模糊数
| $ {C_{\tilde A}} = \frac{{{c^2} + {d^2} + cd - {a^2} - {b^2} - ab}}{{3(c + d - a - b)}}. $ | (8) |
4) 多级模糊综合评判
对类因素中各子因素进行一级模糊综合评判,通过综合子因素的各评价等级对对象取值的贡献,做出单因素评判。由k名专家对子因素uij分别按低、中、高、极高4个评价等级进行隶属度值评分,评分区间为[0, 1],那么第i个因素的等级评判矩阵为
| $ {\mathit{\boldsymbol{R}}_p} = \sum\limits_{k = 1}^K {{{\left[ {{r_{pqk}}} \right]}_{j \times 4}}} {\phi _k}, $ | (9) |
式中:rpqk表示第k个专家对类因素p中第q个子因素的评价,ϕk为各专家评分权重系数。
结合子因素权重集Ap按第p个因素的各子因素进行综合评判,即可得到一级模糊综合评判
| $ {\mathit{\boldsymbol{B}}_p} = {\mathit{\boldsymbol{A}}_p} \cdot {\mathit{\boldsymbol{R}}_p}. $ | (10) |
一级模糊综合评判反映一个因素对评分系数取值的影响,因此R可作为二级模糊综合评判的单因素评判矩阵,表示为
| $ \mathit{\boldsymbol{R}} = {\left[ {\begin{array}{*{20}{l}} {{B_1}}&{{B_2}}&{{B_3}} \end{array}} \right]^{\rm{T}}}. $ | (11) |
结合因素权重集A,对所有因素进行综合评判便得到二级模糊综合评判集
| $ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{A}} \cdot \mathit{\boldsymbol{R}}. $ | (12) |
综合考虑所有影响可靠度分配的因素后,各单元对可靠性水平要求的隶属度,即反映了各单元对可靠度要求的相对高低程度。
单元的综合评价分值即分配权重表示为
| $ \mathit{\boldsymbol{\omega }} = \mathit{\boldsymbol{B}} \cdot {\mathit{\boldsymbol{V}}^{\rm{T}}}. $ | (13) |
产品全寿命周期下的可靠度是各应力共同作用的结果。航天电子产品在寿命周期内需要经历振动、冲击等地面运输环境,温度、湿度等储存环境,振动、冲击、噪声及加速度等发射环境;真空、高低温、微重力、电磁环境、高能粒子辐射等空间环境。为简化模型,不失一般性地假设电子产品主要环境应力为温度、振动、湿度应力,同时忽略各环境应力间未知的相互作用,仅分析温度驻留、温度循环、振动、湿度造成的电子产品失效。因此,产品的可靠度为
| $ R(t) = {R_{\rm{C}}}(t) \cdot {R_{\rm{D}}}(t) \cdot {R_{\rm{v}}}(t) \cdot {R_{\rm{H}}}(t). $ | (14) |
式中:R(t)表示系统可靠性指标;RC(t), RD(t), RV(t)和RH(t)分别为温度循环、温度驻留、振动、湿度应力下的产品可靠度。
系统可靠性指标需要通过试验进行验证,那么应将可靠性以产品各个可靠性乘积的形式分配到上式中,因此采用表 2中三标度层次分析法。
|
|
表 2 三标度层次分析法算法[21] Table 2 Algorithm of three-scale AHP method |
加速应力水平不超过产品工作极限时,失效机理保持不变[22]。试验中单位时间内造成的损伤可通过增加应力的水平进行适当加速。每种故障模式被其中一种或多种应力加速。根据加速因子不变原则,加速应力和正常应力下产品累积失效概率相等:
| $ {F_{\rm{A}}}\left( {{t_{\rm{A}}}} \right) = F(t). $ | (15) |
电子产品寿命服从指数分布,失效函数为
| $ F(t) = 1 - \exp ( - \lambda t). $ | (16) |
转换后发现加速试验本质是对失效率加速:
| $ {\lambda _{\rm{A}}} = {A_{{\rm{Test}}}} \times \lambda = \sum\limits_{m = 1}^M {\left( {\sum\limits_{n = 1}^N {\left( {\sum\limits_{i = 1}^I {\left( {{A_{mni}} \times {\lambda _{mni}}} \right)} } \right)} } \right)} , $ | (17) |
式中:λA和λ分别为加速条件和实际使用下的失效率;λ由系统可靠性指标转化而来;M为功能数,N为单元数,I为失效模式数;λmni为导致子功能m故障时,单元n中故障模式i发生的失效率;Amni为对应的加速因子,可由各应力加速因子结合权重系数推出:
| $ {A_{mni}} = \sum\limits_{j = 1}^J {{\gamma _{ij}}} {A_{mnij}}. $ | (18) |
因此,总的等效加速因子为
| $ {A_{{\rm{Test}}}} = \sum\limits_{m = 1}^M {\left( {\sum\limits_{n = 1}^N {\left( {\sum\limits_{i = 1}^I {\left( {\left( {\sum\limits_{j = 1}^J {{\gamma _{ij}}} {A_{mnij}}} \right) \times {\lambda _{mni}}/\lambda } \right)} } \right)} } \right)} . $ | (19) |
式中:λmni可由相似产品数据或参考GJB/Z 299C或MIL-HDBK-217F标准通过元器件计数法或应力评分法获得。
3.2 加速应力持续时间RDT中用产生等量累积损伤的应力平均持续时间μS_i来衡量产品广义强度,μL_i为实际广义应力的平均持续时间。假设随机应力与随机强度均服从正态分布,应力造成累积损伤的程度与其持续时间成正比,且损伤不超过最大设计极限。基于应力强度干涉模型,各应力下对应的可靠度为
| $ {R_i} = \varPhi \left[ {\frac{{{\mu _{S\_i}} - {\mu _{L\_i}}}}{{\sqrt {{{\left( {a \cdot {\mu _{S\_i}}} \right)}^2} + {{\left( {b \cdot {\mu _{L\_i}}} \right)}^2}} }}} \right], $ | (20) |
式中:a和b表示强度和应力均值标准差的偏差系数。
根据累积损伤模型,假设实际应力(广义强度)的持续时间是应力平均持续时间的K倍。若现场不具备准确的分布信息,可认为最大的标准差为均值的10%,则式(20)可简化为
| $ {R_i}\left( {{k_i}} \right) = \varPhi \left[ {\frac{{\left( {{K_i} - 1} \right) \times 10}}{{\sqrt {K_i^2 + 1} }}} \right]. $ | (21) |
为达到各应力分配的可靠度,放大倍数Ki增大了正常应力水平下统计试验方案中各应力作用的持续时间ti。通过增加应力水平,达到加速的目的,结合各应力加速因子Ai,可得到RADT中各应力实际试验时间,设计出系统RADT试验剖面
| $ {t_{i\_A}} = \frac{{{t_{i\_{\rm{Test}}}}}}{{{A_i}}} = \frac{{{K_i} \cdot {t_i}}}{{{A_i}}}. $ | (22) |
某企业级NAND闪存固态硬盘的基本功能是通过SATA接口与主机系统进行数据存储与交换,主要由主控、缓存、NAND闪存、电源芯片组成,可近似为串联系统。主控作为支持SSD的定制化微处理器,负责NAND闪存与主机间的通信传输;缓存DRAM作为主控的工作内存,并运行固件;NAND闪存包含多块NAND芯片,主要用来存储数据,占据了印制板大部分空间;电源芯片处理5 V直流电压,为各功能单元供电。
由于任务周期内数据处理量较少,不考虑擦写次数对寿命的影响,仅分析温度、振动、湿度等环境应力影响,各应力的加速因子如表 3所示[23]。可靠性指标为10 a寿命的可靠度不低于0.9。假设寿命服从指数分布,因此失效率恒定,约为1.202 7×10-6,MTBF为8.314 3×105 h。
|
|
表 3 各应力加速模型及加速因子 Table 3 Acceleration model and acceleration factors for each stress |
采用模糊层次分析法将可靠性指标分配给各敏感应力。3位专家E1,E2,E3对4个模块进行模糊评判,评判结果见表 4。
|
|
表 4 各单元评价信息表 Table 4 Allocation information for the four units by three experts |
由于经验威望不同,权重占比分别为50%、20%、30%。分别对每个模块计算权重,进行模糊综合评判,得到各模块综合评价分值。综合3位专家的评价,对应因素模糊评价表,加权求和得到各模块的因素模糊数,如表 5所示。
|
|
表 5 单元因素模糊评价信息表 Table 5 Aggregated fuzzy evolution information for the four units |
以主控s1为例进行计算流程说明,表 6所示为主控类因素的子因素权重集,类因素权重集见表 7。通过质心法去模糊后,设计制造U1,系统属性U2,使用维护U3的权重子集分别为A1=(0.3947, 0.6063),A2=(0.3966, 0.162, 0.4413),A3=(0.4863, 0.5137)。3个类因素的权重集为A=(0.1686, 0.6429, 0.1886)。
|
|
表 6 因素U1/U2/U3的权重子集评价表 Table 6 Evaluation results of subfactors of U1/U2/U3 |
|
|
表 7 类因素权重集评价表 Table 7 Wight evaluation results of factor sets |
各专家对类因素中各子因素按4类评价级进行隶属度评分,对3个评判矩阵求加权平均,得到3个类因素的等级评判矩阵和模糊评判集如表 8所示。构造二级模糊综合评判的单因素评判矩阵R,那么二级模糊综合评判集B为[0.1521 0.1845 0.4663 0.4248],因此主控s1的综合评价分值
|
|
表 8 类因素等级评判矩阵和模糊评判集 Table 8 Rating matrix and fuzzy evaluation results of factor sets |
继续以主控s1为例,通过表 2中三标度层次分析法确定各模块所受环境应力的权重γ=[γ1 γ2 γ3 γ4]T。比较矩阵C1=[1 2 2 2; 0 1 0 2; 0 2 1 2; 0 0 0 1],主控各环境应力权重为γ1=[0.4859 0.1321 0.2953 0.0867]。重复以上步骤,依次得到闪存、缓存、电源芯片的各环境应力权重为γ2=[0.3158 0.3024 0.3158 0.0606],γ3=γ4=[0.5638 0.2634 0.1178 0.055]。
因此,可以确定各环境应力的归一化权重系数w,环境应力可靠性分配结果如表 9所示。
|
|
表 9 各应力指标分配及加速试验剖面参数 Table 9 Allocated reliability indexes and acceleration test profile parameters for each stress |
产品使用环境和加速应力如表 10所示,各应力分配权重系数wj、分配的可靠度Rj和失效率λj、加速因子Aj、试验持续时间放大系数Kj等试验剖面参数如表 9所示。表 11详细描述了系统加速因子的计算流程。
|
|
表 10 使用环境和加速环境应力条件 Table 10 Stresses in use and acceleration conditions |
|
|
表 11 系统加速因子计算流程 Table 11 Calculation procedure of the overall acceleration factor |
在计算系统加速因子时,IEC62506标准中假设温度循环和振动激发同种失效模式,而温度驻留和湿度造成另一种失效模式,即ATest=ACAV+ADAH。显然加速倍数过大,会缩短验证时间,提高使用方风险,扩大“存伪”风险;Chen等[7]基于极小值原则,选取各应力中最小加速因子作为总加速系数,即ATest=min{AC, AV, AD, AH},延长试验验证时间,增加了样品接收难度,增大了生产方风险,且过于保守,加大了“去真”风险。
在试验总时间方面,假设生产方风险和使用方风险均为30%,鉴别比为3,选取短时高风险定时试验21号方案[21]。正常应力下总累积试验试验为1.1MTBF=9.145 7×105台时,试验时间太长。采用本文方案,加速条件下的总验证试验时间ttest=t0/ATest=96 826台时,若试验样本数为100,那么总试验时间为968.26 h,时间和费用大幅缩短。换言之,要验证该固态硬盘正常工作条件下10 a的可靠度不低于0.9,只需对100块样品按照可靠性鉴定试验剖面,结合各应力加速因子,开展968.26 h的无替换定时截尾试验,若故障数为0,认为产品符合指标要求,接收批产品,若故障数不为0,认为产品达不到指标要求,拒收批产品。
5 结论与展望本文针对多失效系统级产品提出基于模糊层次分析法的系统加速验证试验设计。主要结论如下:
1) 结合故障物理与统计分析,通过引入模糊逻辑和层次分析法提出可靠性分配新方法,基于指标分配到各环境应力的新思路研究系统加速验证试验模型,并且建立加速试验剖面设计方法。
2) 基于加速因子不变原则推导出系统加速因子计算方法,便于构建加速试验剖面,将环境试验方法与可靠性试验方法联系起来。
下一步的研究重点是考虑空间辐射、电应力、工况加速等其他应力类型,并研究专家权重、应力种类、加速因子、应力强度干涉模型类型和参数等不确定性因素对本方法的影响。
| [1] |
International Electrotechnical Commission. TC 56-methods for product accelerated testing: IEC 62506: 2013[S/OL]. (2013-06-18)[2019-06-02]. https://webstore.iec.ch/publication/7139.
|
| [2] |
中国人民解放军总装备部. GJB 899A-2009, 可靠性鉴定和验收试验[S].北京: 中国标准出版社, 2009.
|
| [3] |
Guo H, Liao H. Methods of reliability demonstration testing and their relationships[J]. IEEE Transactions on Reliability, 2012, 61(1): 231-237. |
| [4] |
Yadav O, Singh N, Goel P. Reliability demonstration test planning:a three dimensional consideration[J]. Reliability Engineering & System Safety, 2006, 91(8): 882-893. |
| [5] |
Li P, Li C, Dang W. Accelerated reliability demonstration testing design based on reliability allocation of environmental stresses[J]. Quality & Reliability Engineering International, 2017, 33(7): 1425-1435. |
| [6] |
Xu J, Hu Q, Yu D, et al. Reliability demonstration test for load-sharing systems with exponential and Weibull components[J]. Plos One, 2017, 12(12): e0189863. |
| [7] |
Chen Y, Jing H, Liao X, et al. Methods to determine stress profile in ALT based on theoretical life models[J]. Chinese Journal of Aeronautics, 2015, 28(3): 729-736. |
| [8] |
Chen S, Lu L, Li M. Multi-state reliability demonstration tests[J]. Quality Engineering, 2017, 29(3): 431-445. |
| [9] |
Kleyner A. Effect of field stress variance on test to field correlation in accelerated reliability demonstration testing[J]. Quality & Reliability Engineering International, 2015, 31(5): 783-788. |
| [10] |
Xu J, Yu D, Xie M, et al. An approach for reliability demonstration test based on power-law growth model[J]. Quality & Reliability Engineering International, 2017, 33(8): 1719-1730. |
| [11] |
Chang M, Kwon Y, Kang B. Design of reliability qualification test for pneumatic cylinders based on performance degradation data[J]. Journal of Mechanical Science & Technology, 2014, 28(12): 4939-4945. Doi:10.1007/s12206-014-1115-1 |
| [12] |
Xu D, Wei Q, Chen Y, et al. Reliability prediction using physics-statistics-based degradation model[J]. IEEE Transactions on Components Packaging & Manufacturing Technology, 2015, 5(11): 1573-1581. |
| [13] |
Jin G, Matthews D. Reliability demonstration for long-life products based on degradation testing and a Wiener process model[J]. IEEE Transactions on Reliability, 2014, 63(3): 781-797. |
| [14] |
Luo W, Zhang C, Chen X, et al. Accelerated reliability demonstration under competing failure modes[J]. Reliability Engineering & System Safety, 2015, 136(136): 75-84. |
| [15] |
Luo W, Zhang C, Chen X, et al. Reliability demonstration based on accelerated degradation testing for unknown model parameters[J]. Proceedings of the Institution of Mechanical Engineers Part O-Journal of Risk & Reliability, 2013, 227: 162-172. |
| [16] |
Zhang J, Ma X, Zhao Y. Reliability demonstration for long-life products based on hardened testing method and Gamma process[J]. IEEE Access, 2017, 5: 19322-19332. |
| [17] |
谭源源.装备贮存寿命系统加速试验技术研究[D].长沙: 国防科学技术大学, 2010.
|
| [18] |
Yadav O, Zhuang X. A practical reliability allocation method considering modified criticality factors[J]. Reliability Engineering and System Safety, 2014, 129: 57-65. |
| [19] |
Rosmaini A, Shahrul K, Ishak A, et al. Failure analysis of machinery component by considering external factors and multiple failure modes:a case study in the processing industry[J]. Engineering Failure Analysis, 2012, 25: 182-192. |
| [20] |
Kim K, Yang Y, Zuo M. A new reliability weight for reducing the occurrence of severe failure effects[J]. Reliability Engineering and System Safety, 2013, 117: 81-88. |
| [21] |
张天军, 苏琳, 乔宝明, 等. 改进的层次分析法在煤与瓦斯突出危险等级预测中的应用[J]. 西安科技大学学报, 2010, 30(5): 536-542, 547. |
| [22] |
Limon S, Yadav O, Liao H. A literature review on planning and analysis of accelerated testing for reliability assessment[J]. Quality & Reliability Engineering International, 2017, 33(1): 2361-2383. |
| [23] |
Escobar L A, Meeker W Q. A review of accelerated test models[J]. Statistical Science, 2006, 21(4): 552-577. |
 2021, Vol. 38
2021, Vol. 38 


