中国科学院大学学报  2021, Vol. 38 Issue (1): 114-120   PDF    
引用本文
张文昭, 平劲松, 李文潇. 3种典型的太阳系大行星历表的对比分析[J]. 中国科学院大学学报, 2021, 38(1): 114-120.
Zhang W Z, Ping J S, Li W X. Comparison and analysis of three kinds of typical solar system planetary ephemeris[J]. Journal of University of Chinese Academy of Sciences, 2021, 38(1): 114-120.
3种典型的太阳系大行星历表的对比分析
张文昭1, 平劲松2,3, 李文潇2,4     
1. 北京师范大学天文系, 北京 100875;
2. 中国科学院大学天文与空间科学学院, 北京 100049;
3. 中国科学院国家天文台, 北京 100012;
4. 中国科学院新疆天文台, 乌鲁木齐 830011
2019年6月3日 收稿; 2019年8月22日 收修改稿
基金项目: 科技部国家重点研发计划项目(2016YFE0120000)、中国科学院国际伙伴计划及俄乌白国际合作重点项目、国家自然科学基金(41590851)资助
通信作者: 张文昭，E-mail:wenzhaozhang@bnu.edu.cn
摘要: 美国DE系列、法国INPOP系列和俄罗斯EPM系列数值星历表是目前公认处于世界领先的3种行星数值历表。计算100 a（1960—2060年）间，3种数值历表中大行星（包含月球）相对地球和相对太阳系质心的位置坐标差分最大值及均方根。结果表明，3种历表对太阳系质心的测量存在百米到公里量级的偏差，EPM2017与其他两个相差较大。考虑相对地心的位置，水星和金星的历表精度在百米量级；火星的历表精度在百米到公里量级；木星和土星的历表精度在几公里到几十公里量级；天王星和海王星的历表精度在几百公里到几千公里量级；月球历表的精度在分米到米量级，其径向距离精度在分米量级。此结果为地月空间科学实验及深空探测应用提供了支持和依据。
关键词: 星历表    精度    比较    
Comparison and analysis of three kinds of typical solar system planetary ephemeris
ZHANG Wenzhao1, PING Jinsong2,3, LI Wenxiao2,4     
1. Astronomy Department, Beijing Normal University, Beijing 100875, China;
2. School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 100049, China;
3. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China;
4. Xinjiang Astronomical Observatory, Chinese Academy of Sciences, Urumqi 830011, China
Abstract: The US DE series, the French INPOP series, and the Russian EPM series ephemerides are three types of the world's leading numerical planetary ephemerides. In this paper, the maximum values and the root-mean-squares of the positions of the major planets (including moon) relative to the earth and the barycenter of the solar system in the three numerical ephemerides during one hundred years (1960-2060) are calculated. The results show that the deviation levels of the measurements about the solar system barycenter range from hundred meters to kilometers, and the differences between EPM2017 and the other two are large. Taking the earth as the reference point, the accuracies for Mercury and Venus are at one hundred meter level. The accuracy of Mars ranges from hundred meters to kilometers. The accuracies for Jupiter and Saturn range from several kilometers to tens of kilometers. The accuracies for Uranus and Neptune range from several hundred kilometers to thousands of kilometers. The accuracy of Lunar ephemeris ranges from decimeter to meter, and its radial distance accuracy is at the decimeter level. These results provide support and basis for the cislunar space science experiment and deep space exploration application.
Keywords: planetary ephemeris    accuracy    comparison    

大行星历表的构建是一个基本的动力学时空框架工作，深受各个天文与航天大国和地区的重视；大行星历表的用途极为广泛，从早期的观天授时，到近现代的深空探测，都需要太阳、月球和行星的精确空间位置信息作为支撑；大行星历表的精度也在随着时间和科技的发展而不断提高。到了近代，人类已经可以根据经典的摄动分析理论给出精度极高的解析星历解[1]。自20世纪中叶开始，计算机的发明和广泛应用，使得采用数值方法得到更加精确的星历成为可能。随着20世纪60年代开始的月球和深空探测不断开展、激光和雷达天文技术的不断进步，太阳系内大天体的观测数据不断增多，观测精度不断提高，使得星历数值解的精度也随之提高，逐步超越解析解。目前，数值法已经成为世界上采用最多的计算精密行星历表的方法。同时，高精度的数值行星历表也为月球和深空探测[2-3]、引力理论模型检验[4]等提供了必要的辅助作用。

来自不同国家的多个团队曾经开展过月球和大行星历表——太阳系空间参考基准的独立研究和构建。目前，世界上使用非常广泛的、精度很高的数值星历表有美国JPL(Jet Propulsion Laboratory，喷气推进实验室)研发的DE①(Development Ephemeris)系列行星历表[5-6]、法国巴黎天文台研发的INPOP②(Intégration Numérique Planétaire de l′Observatoire de Paris)系列行星历表[7-8]以及俄罗斯科学院应用天文研究所研发的EPM③(Ephemerides of Planets and the Moon)系列行星历表[9]。此外，德国、中国等国家也在开发自己的星历表。在几种行星历表中，由于开展了大量的月球与行星探测等原因，近年来JPL星历表使用变得更为广泛，除用于不同国家的月球深空探测任务之外，还被嵌入各类天体测量、卫星导航等最高精度需求的分析软件代码之中。但由于其开发软件源代码不是开源的，限制了其他科研工作者在其上进一步开发的可能性。法国虽然很早就开始太阳系行星历表的计算，但在1998年才正式开始编制INPOP数值星历表。苏联则是在1974年开始EPM星历表的编制。目前，由欧空局ESA支持的INPOP星历表和俄罗斯的EPM星历表，其精度基本上和JPL星历表相当[10-13]。国内的天文学家也在为生成自己的行星历表而不断努力，紫金山天文台2003年发布PMOE2003历表框架[14-16]，之后又对其进行了修正，但由于观测数据资料的受限，其精度尚未达到上述历表的水平。

①   DE星历表下载地址：ftp://ssd.jpl.nasa.gov/pub/eph/planets/

②   INPOP星历表下载地址：http://www.geoazur.fr/astrogeo/?href=observations/base

③   EPM星历表下载地址：ftp://ftp.iaaras.ru/pub/epm/

DE行星历表、INPOP行星历表和EPM行星历表代表目前世界上数值星历表演算的领先水平，对其精度进行比较和分析，具有重要的意义。同时，可为中国正在进行的月球探测和即将进行的火星、金星探测任务提供参考依据。本文以DE436、INPOP17a和EPM2017为例，比较3个数值历表中主要行星位置分量的差异，对其产生的原因进行简单分析。

1 行星历表简介 1.1 DE系列

为支持空间探测计划，从20世纪60年代起，美国宇航局JPL开始编制行星历表DE系列，现在最新发布的版本为DE437。DE系列星历表的发布年份没有规定，取决于当时的空间探测任务和新的观测资料。它被全球天文年历、深空探测等广泛应用。目前应用比较多的DE430发布于2013年4月，包含月球天平动，采用IAU(International Astronomical Union)1980章动模型，时间跨度为JED 2287185.5(公元1550年1月1日)—JED 2688973.5(公元2650年1月22日)。相比于之前版本的行星历表，它使用更多的月球和空间探测器观测数据进行拟合，包含更多的LLR(Lunar Laser Ranging)和更新的GRAIL(Gravity Recovery and Interior Laboratory)月球重力模型。利用进入水星轨道的信使号宇宙飞船(MESSENGER)测量数据改进水星轨道；利用更多的空间探测器(金星快车(VEX)、火星快车(MEX)、火星奥德赛号(ODY)以及火星轨道探测器)甚长基线干涉(VLBI)观测数据，改进金星、地球和火星轨道；利用更多的卡西尼号航天器观测数据改进土星轨道。冥王星的轨道也通过额外的观测得到改进。木星、天王星和海王星的轨道虽然并没有太多的改变，但拟合时还是采用了更多的观测数据[17]。本文讲述的DE436是为了“朱诺”号木星探测器项目而发布的版本，在DE430的基础上更新了木星星历。

1.2 INPOP系列

INPOP行星历表是法国在1998年IMCCE成立后，才正式开始编制的。2008年发表了INPOP06，这本历书在动力学模型和拟合方法上与JPL参考历书接近，INPOP08和INPOP10a采用ESA提供的MEX(Mars Express)和VEX(Venus Express)跟踪资料，以及飞船掠过水星(Messenger)、木星(Pioneer)、土星(Cassini)、天王星和海王星(Voyager2)的测距资料、LLR资料(包括Lunar Prospector Mission无线电和激光跟踪)、新的行星和月球历书模型时间(TT(Terrestrial Time，地球时)和TDB(Barycentric Dynamical Time，质心力学时)的关系、运动相对论方程式中的矩阵和采用固定的AU(Astronomical Unit，天文单位，其数值取地球和太阳之间的平均距离)值拟合太阳引力质量和新的平差方法。2013、2014年分别发布INPOP10e和INPOP13c。2017年发布INPOP17a[9]，即本文中采用的版本。INPOP17a在月球星历计算中，拟合47 a(1969—2016年)的LLR数据和GRASSE站提供的2 a(2015—2017年)红外激光测距数据(IR LLR)，后者的加入改进了月球轨道和自转动力学模型。

1.3 EPM系列

1974年苏联应用天文研究所(IAA)开始编制行星历表EPM，最初的历表为EPM87，以后逐步改进。2006年之后，俄罗斯年历采用EPM2004，以后又有EPM2008、EPM2011[18]和EPM2013。更新的EPM2015，包括1913—2014年各种类型观测，从经典光学观测至飞船的无线电观测，共120 000+次测量。更多的数据使得其历表精度相比之前有了很大提高。本文使用的是其发布的最新版本EPM2017，增加了2015版本之后的LLR和空间飞行器的观测数据，并改进了一些新的模型和新的估计算法。与之前的版本相比，在以下几个方面有所增加或改进：

a) Lense-Thirring加速度模型；

b) 相对重心的定义；

c) 将太阳作为一个正常物体的加速度的模型；

d) 小行星带和柯伊伯带的新模型；

e) 小行星质量和轨道估计；

f) EPM2015之后的航天器和LLR数据。

2 星历表比较 2.1 大行星坐标位置的比较

为了方便对3种历表进行对比，选取发布日期相近的DE436、INPOP17a和EPM2017，这3个星历表都是在2017年发布的，参考系采用质心天球参考系(Barycentric Celestial Reference System，BCRS)，坐标系指向与国际天球参考框架(International Celestial Reference Frame，ICRF)一致，原点在太阳系质心，其坐标轴指向由一组精确观测的河外射电源的坐标实现[19]，时间系统都采用TDB，同时都包含近期的LLR和空间探测器测量数据。对这3个数值历表进行比较，基本上可以反映目前世界上数值行星历表的探测精度，也为中国进行自己的数值行星历表建设提供依据。深空探测一般是以太阳系质心为参考原点，同时，由于射电和光学等望远镜大多位于地球表面，观测数据的地基属性较为明显。因此，比较太阳系内大天体相对太阳系质心和相对地球的位置矢量，对天文实际观测和观测策略研究，均有指导意义。本文分别计算各大行星(含地球、月球)相对太阳系质心和相对地球的最大偏差(MAX)和均方根(RMS)，结果见表 1和表 2。选取数据的时间跨度为1960—2060年，时间步长为0.5 d。

表 1 大行星(含地球、月球)相对太阳系质心的最大偏差(MAX)和均方根(RMS)(1960—2060年) Table 1 Maximum deviation (MAX) and root mean square (RMS) values of major planets (including Earth and Moon) relative to the center of mass of the solar system (1960-2060)  

表 2 大行星相对地球的最大偏差(MAX)和均方根(RMS)(1960—2060年) Table 2 Maximum deviation (MAX) and root mean square (RMS) values of major planets relative to the Earth (1960-2060)  

从上述结果可以看出，以地球为参考，在对太阳系质心的测量上，INPOP17a和DE436之间存在百米量级的偏差，EPM2 017则与这两个相差较大，偏差达几公里甚至十几公里，这是由于EPM在动力学模型中考虑了TNO(Trans-Neptunian Objects，海王星外天体)摄动[20]。考虑相对地心的位置偏差，水星和金星的历表精度在百米量级；火星的历表精度在百米到公里量级；木星和土星的历表精度在几公里到几十公里量级；天王星、海王星的历表精度在几百公里到几千公里量级；月球历表的精度在分米到米量级。大行星的数值历表比较结果显示，EPM2017与另外两个差别稍大；而月球历表则是INPOP17a与另外两个差别稍大。观测数据丰富的时段，3个行星历表的差别相对较小，之前和之后的都在逐渐增大，以月球最为明显(如图 1所示)，这可能是由于积分模型和参数选择不同造成的。虽然3个星历表之间的差别不能说明对行星位置测量的绝对误差，但可以从侧面反映出当今世界上行星位置的测量精度，对中国进行深空探测具有重要的参考价值。

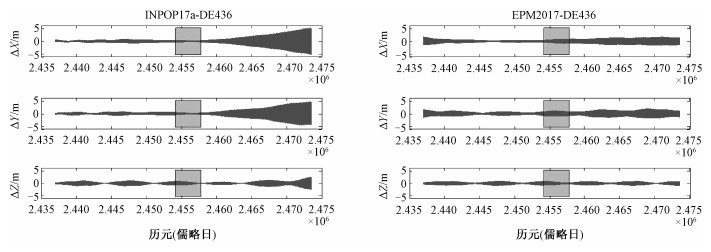
Download:
方块表示星历表发布前10 a。 图 1 3个星历表在月球星历上的差分结果(1960—2060年) Fig. 1 The differences between the three ephemerides on the Lunar ephemeris (1960-2060)

为了更好地说明天体位置受观测资料的影响，提取星历表发布之前10 a左右的数据，计算3个星历表中相对太阳系质心和相对地球质心的最大角度偏差，结果如表 3所示。

表 3 典型行星(含月球)相对太阳系质心和地球质心的最大角度偏差(2007—2017年) Table 3 Maximum angular deviations of typical planets (including Moon) to the centroid of the solar system and the centroid of the Earth (2007-2017)  

在星历表发布之前的10 a中，观测资料都比较丰富，相对于地球质心来说，水、金、火、月都可以做到零点几个mas，土星由于卡西尼号的观测资料，差别也可以达到零点几个mas。木星、天王星和海王星相对差别较大。相对于太阳系质心，由于额外考虑了TNO，EPM与其他两个相差较大。

2.2 行星历表的自洽性

从上面的比较结果可以看出，3个数值历表中对太阳系质心位置的确定具有明显差异，尤其是EPM2017，与其他两个历表差异更大。为明确这种对太阳系质心位置的差异是否会影响相对地球的位置，本文还通过从星历表读出的各大行星相对太阳系质心的位置和地球相对于太阳系质心的位置计算各大行星相对地球的位置，与从星历中直接读取的大行星相对地球位置进行比较。从比较结果来看，3个星历表中大行星本身的误差都在厘米量级以下，JPL月球星历本身误差为毫米量级，EPM和INPOP月球星历本身误差甚至达到10-5 m。相对于3个行星历表间的差异，其本身误差可以忽略不计。由此可见，3个星历表本身还是自洽的。

2.3 地月距离的比较与分析

月球是距离我们最近的自然天体，对月球的测量和研究一直是天文中的重要部分。高精度月球激光测距技术和各种月球空间探测器、探测飞船带来了高精度的测量数据，使得人们对月球距离的测量达到十分精确的程度。为了更好地说明问题，我们把距离分量从直角坐标转化为球面坐标，并且只讨论我们最关心的地月径向距离。从图 2可以看出，在行星历表发布之前的10~20 a内，由于观测数据量比较充分，3个星历表在地月距离上得到的结果差别不大，径向距离差别基本上在10-1 m的量级。而在之前和之后的差分结果相对发散，主要是不同机构选取的模型参数不同造成的累积误差。为了更加精细地看出三者的差别，将2007—2017年的差分结果放大(图 3)。可以看到，径向分量上INPOP和JPL的差分结果在0.2 m上下震荡，幅度约0.05 m，EPM和JPL的结果更加接近，差分结果保持在0.05 m以内，这可能是3个星历表中选取的参数不同造成的。

Download:
方块表示星历表发布前10 a。 图 2 3个星历表在月球径向距离上的差分结果(1960—2060年) Fig. 2 The differences between the three ephemerides in the radial distance of the Moon (1960-2060)

Download:
图 3 3个星历表在月球径向距离上的差分结果(2007—2017年) Fig. 3 The differences between the three ephemerides in the radial distance of the Moon (2007-2017)
3 结论及展望

本文选取美国喷气推进实验室研发的DE436、法国巴黎天文台研发的INPOP17a以及俄罗斯科学院应用天文研究所研发的EPM2017这3个最近发布的、精度处于世界上领先水平的数值行星历表，对历表中大行星(包含月球)相对地球以及相对太阳系质心的位置坐标进行差分计算及简单分析。结果表明，虽然3个历表本身都是自洽的，但对太阳系质心的测算存在百米到公里量级的偏差，其中EPM2017跟其他两个相差较大。考虑相对地心的位置偏差，水星和金星的历表精度在百米量级；火星的历表精度在百米到公里量级；木星和土星的历表精度在几公里到几十公里量级；天王星、海王星的历表精度在几百公里到几千公里量级；月球历表的精度在分米到米量级，其径向距离精度在分米量级。这对中国接下来要进行的深空探测工程具有相当的参考意义。特别是各大行星相对于太阳系质心和相对于地球的不同精度，需要我们在实际应用中特别注意。

中国的“嫦娥”探月工程持续进行，月球激光测距、无线电测距技术的发展，观测数据越来越多，对中国独立研发自己的月球历表具有极大的促进作用。地月距离的精确测量是研究月球物理天平动的基础，了解其测量精度量级，为下一步进行月球物理天平动的研究提供了重要的参考价值。

参考文献
[1]
金文敬. 太阳系行星和月球历表的发展[J]. 天文学进展, 2015, 33(1): 103-121.
[2]
樊敏, 董光亮, 邓雪梅, 等. 深空探测器测轨数据用于历表研制的分析[J]. 飞行器测控学报, 2012, 31(6): 11-16.
[3]
樊敏, 董光亮, 黄勇, 等. 金星探测器测定轨系统设计与试验验证[J]. 飞行器测控学报, 2015, 34(1): 48-56.
[4]
倪维斗. 相对论性引力理论的实验基础及测试[J]. 紫金山天文台台刊, 2004, 23(1-4): 33-52.
[5]
邓雪梅, 樊敏, 谢懿. JPL行星历表的比较及评估[J]. 天文学报, 2013, 54(6): 550-561. Doi:10.3969/j.issn.0001-5245.2013.06.005
[6]
杨永章, 李金岭, 平劲松, 等. NASA历表在深空导航中的发展和比较[J]. 深空探测学报, 2017, 4(1): 89-98.
[7]
Fienga A, Laskar J, Kuchynka P, et al. The INPOP10a planetary ephemeris and its applications in fundamental physics[J]. Celestial Mechanics and Dynamical Astronomy, 2011, 111(3): 363-385.
[8]
Viswanathan V, Fienga A, Gastineau M, et al. INPOP17a planetary ephemerides[J]. Notes Scientifiques et Techniques de l'Institut de mécanique céleste, (ISSN 1621-3823), #108, ISBN 2-910015-79-3, 2017, 108: 1-39.
[9]
Vasilyev M V, Yagudina E I. 俄罗斯应用天文研究所月球历表研究现状[J]. 深空探测学报, 2014(3): 187-191.
[10]
Viswanathan V, Fienga A, Minazzoli O, et al. The new lunar ephemeris INPOP17a and its application to fundamental physics[J]. MNRAS, 2018, 476(2): 1877-1888.
[11]
Pitjeva E V, Pitjev N P. Development of planetary ephemerides EPM and their applications[J]. Celestial Mechanics and Dynamical Astronomy, 2014, 119(3/4): 237-256.
[12]
Fienga A, Laskar J, Exertier P, et al. Numerical estimation of the sensitivity of INPOP planetary ephemerides to general relativity parameters[J]. Celestial Mechanics and Dynamical Astronomy, 2015, 123(3): 325-349. Doi:10.1007/s10569-015-9639-y
[13]
Yagudina E I. Lunar numerical theory EPM2008 from analysis of LLR data[C]//Proceedings of Journees, 2008: 61-64.
[14]
李广宇, 倪维斗, 田兰兰. PMOE2003精密行星历表框架(Ⅰ)数学模型[J]. 紫金山天文台台刊, 2003, 22(3/4): 12-30.
[15]
李广宇, 田兰兰. PMOE2003精密行星历表框架(Ⅱ)积分器和程序设计[J]. 紫金山天文台台刊, 2003, 22(3/4): 32-56.
[16]
李广宇, 田兰兰. PMOE2003行星历表框架(Ⅴ)历表文件的生成和使用[J]. 紫金山天文台台刊, 2004, 23(1-4): 160-170.
[17]
Folkner W M, Williams J G, Boggs D H, et al. The planetary and lunar ephemerides DE430 and DE431[J]. Interplanetary Network Progress Report, 2014, 196: 1-81.
[18]
Pitjeva E V. Updated IAA RAS planetary ephemerides-EPM2011 and their use in scientific research[J]. Solar System Research, 2013, 47(5): 386-402. Doi:10.1134/S0038094613040059
[19]
刘佳成, 朱紫. 2000年以来国际天文学联合会(IAU)关于基本天文学的决议及其应用[J]. 天文学进展, 2012, 30(4): 411-437.
[20]
Pavlov D A, Williams J G, Suvorkin V V. Determining parameters of Moon's orbital and rotational motion from LLR observations using GRAIL and IERS-recommended models[J]. Celestial Mechanics and Dynamical Astronomy, 2016, 126(1-3): 61-88.