2. 中国科学院大学材料科学与光电技术学院材料科学与光电工程中心, 北京 100049
2. Center of Materials Science and Optoelectronics Engineering, College of Materials Science and Opto-Electronic Technology, University of Chinese Academy of Sciences, Beijing 100049, China
毛细现象是一种常见的物理现象,如毛细管中液体的上升或下降都是毛细力产生的结果。毛细力是三相界面气液表面张力、固液界面张力以及气固表面张力三力合力的结果[1]。通过改变界面张力,可以控制液体向某一方向定向运动[2-3],也可以使两种不互溶的液相相互溶解, 在石油开采、静电喷雾等领域有大量应用[4-5]。改变界面张力的方式有很多,常用的方法有加热、加电以及通过光照等[6-10]。通过施加电场改变界面张力的方式最为简便且响应迅速,因此研究最为广泛。利用电毛细运动回收有价金属在有色冶金中早有研究[11-15]。张家雯等[16]通过模拟证明交流电渣重熔体系中存在电毛细震荡。张国堤[17]研究Ga-In合金及Wood合金在NaOH水溶液中的电毛细运动速度与电压的关系,但其研究的液滴过大,且部分表面接触了容器底面,形状不是完整的球形,所得结果并不能全面地反映电毛细运动的规律。本文研究常温下液态GaInSn合金在电解质溶液空间中重力作用下的电毛细运动,通过视频记录和图像处理的手段,得到液滴电毛细瞬时的运动规律。为了降低金属液滴在电解质溶液中的沉降速度,便于实验操作和简化实验模型,本文采用NaOH-淀粉混合液作为电解质溶液相。
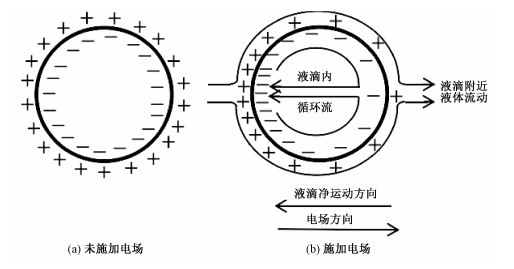
1 实验方法 1.1 实验原理置于电解质溶液中的金属液滴,在金属液滴-电解质溶液界面会处形成一个双电层,如图 1(a)所示。施加外电场时,双电层的电荷会受到施加电场的影响,离子在扩散层中发生重排,沿液滴表面形成电荷密度的梯度。离子的重新分布意味着双电层和界面的组成发生了变化,导致界面张力发生变化。因为界面张力与表面过剩电荷密度有关,所以在液滴表面就产生了界面张力梯度。为了使系统的吉布斯能最小,界面处流体将从低界面张力区流向高界面张力区,驱动液滴内部产生循环流动,如图 1(b)所示。这种循环流动将影响电解质边界层内的流体流动,由此产生的黏性摩擦力使整个液滴移动[18-22]。
|
Download:
|
| 图 1 电毛细运动原理图 Fig. 1 Schematic diagram of electrocapillary movement | |
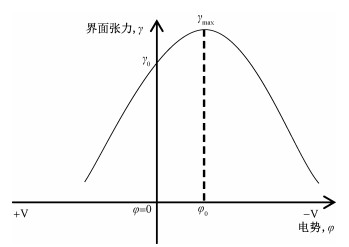
图 2是常见的界面张力与外加电势的关系曲线形状,一般称为电毛细曲线。曲线的形式一般为倒U型,从图中可以看出,在外加电势为0 V时,界面张力为γ0,并不是界面张力的最大值。因为此时在界面处由于正负电荷的吸附能力不同已经形成双电层,如图 1(a)所示,同性电荷相互排斥从而降低了界面张力。外加电势使溶液的电势逐渐降低,金属侧界面的负电荷逐渐减少,相应的溶液侧界面的正电荷也逐渐减少,从而界面张力逐渐增加。当界面张力增加到最大值γmax时,界面处净电荷为0,此时电势称为零电荷电势φ0。
|
Download:
|
| 图 2 电毛细曲线 Fig. 2 Electrocapillary diagram | |
该曲线方程可由Lippmann方程和微分电容方程导出:
| $ {\frac{{\partial \gamma }}{{\partial \varphi }} = - {q_{\rm{m}}} = - {q_{\rm{s}}} = - \varepsilon ,} $ | (1) |
| $ {c = \frac{{\partial {q_{\rm{m}}}}}{{\partial \varphi }},} $ | (2) |
式中:γ为界面张力(N/m);φ为溶液相对于金属的外加电势差(V);qm为金属侧界面过剩电荷密度(N·m-1·V-1);qs为溶液侧界面过剩电荷密度(N·m-1·V-1);ε为界面过剩电荷密度(C/m2);c为双电层微分电容(C/V)。
将式(1)代入式(2), 在图 2中φ=φ0,γ=γmax条件下,经积分可得到抛物线型的电毛细曲线方程
| $ \gamma = {\gamma _{\max }} - \frac{c}{2}{\left( {\varphi - {\varphi _0}} \right)^2}. $ | (3) |
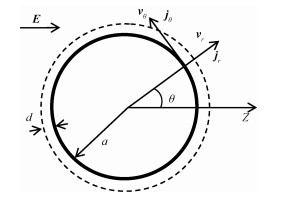
当金属液滴在施加匀强电场达到稳定后,可将液滴周围电势分布求解看作静电场电势求解问题。以液滴球心为球坐标系的原点,过球心取一个截面如图 3。图中E为施加电场的电场强度(V/m);a为金属液滴半径(m);d为双电层厚度(m);球坐标的极轴和方位角分别为Z和θ;vθ为流体的切向速度(m/s);vr为流体的径向速度(m/s);jθ为切向的电流密度(A/m2);jr为径向的电流密度(A/m2)。
|
Download:
|
| 图 3 电场作用下金属液滴在溶液中的参数表示 Fig. 3 Parameter representation of metal droplet in solution under electric field | |
因为金属液滴电导率极大,可看作等势体,设金属液滴的电势为0 V。因为在双电层以外的区域内净电荷密度为0,所以电势可表示为拉普拉斯方程
| $ {\nabla ^2}\varphi = 0. $ | (4) |
在球坐标系下,由对称性可知φ仅与变量r和θ有关,则通解[23]为
| $ \varphi = \sum\limits_{n = 0}^\infty {\left( {{A_n}{r^n} + {B_n}\frac{1}{{{r^{n + 1}}}}} \right)} {P_n}(\cos \theta ),n = 0,1,2, \cdots , $ | (5) |
式中:An、Bn为待定常数,Pn(cosθ)为勒让德多项式。
在r趋向于无穷远处时,应有
| $ {\varphi _{r \to \infty }} = Ez = Er\cos \theta , $ | (6) |
式中:z为无穷远处的某点位移在电场方向上的投影(m)。
将式(6)代入式(5),可以化为
| $ \varphi = \mathit{\boldsymbol{E}}a\left[ {\frac{r}{a} + {C_1}{{\left( {\frac{a}{r}} \right)}^2}} \right]\cos \theta , $ | (7) |
式中:C1为待定常数。
在r=a+d处将质量传输的微分方程转化为电荷传输微分方程
| $ \frac{{\partial \varepsilon }}{{\partial t}} + \nabla \cdot \left( {\varepsilon \mathit{\boldsymbol{v}} - {D_{\rm{s}}}\nabla \varepsilon } \right) = 0, $ | (8) |
式中:v为流体速度(m/s);Ds为电荷表面扩散系数(m2/s)。当双电层处流体为定常流动时,表面过剩电荷密度将不随时间变化,且不发生扩散作用,电荷传输主要受流体对流作用,因此式(8)将简化为
| $ \nabla \cdot (\varepsilon \mathit{\boldsymbol{v}}) = \frac{{\partial \varepsilon {\mathit{\boldsymbol{v}}_\theta }}}{{r\partial \theta }} + \frac{{\partial \varepsilon {\mathit{\boldsymbol{v}}_r}}}{{\partial r}} = {\mathit{\boldsymbol{j}}_\theta } + {\mathit{\boldsymbol{j}}_r} = 0, $ | (9) |
式中jr还可用欧姆定律表示为
| $ {\mathit{\boldsymbol{j}}_r} = \sigma {\mathit{\boldsymbol{E}}_r} = \sigma \left( {\frac{{\partial \varphi }}{{\partial r}}} \right){\mathit{\boldsymbol{r}}^0}, $ | (10) |
式中:Er为界面法向电场强度(V/m);σ为溶液的电导率(S/m);r0为径向的单位向量。为便于推导,假设ε为常数,并令
| $ {\mathit{\boldsymbol{v}}_\theta } = {\mathit{\boldsymbol{v}}_0}\sin \theta , $ | (11) |
式中:v0为待定速度(m/s)。由于a>>d,可认为在r=a处和r=a+d处的速度以及电势相同。联立式(7)、式(9)、式(10)和式(11)可得
| $ \varphi = \left[ {r + \left( {\frac{1}{2} - \frac{{\varepsilon {v_0}}}{{\sigma \mathit{\boldsymbol{E}}a}}} \right)} \right]\mathit{\boldsymbol{E}}a\cos \theta . $ | (12) |
由于已经设金属液滴电势为0 V,所以双电层的电势差Δφ为
| $ \Delta \varphi = {\varphi _{r = a + d}} - {\varphi _{{\rm{metal }}}} \approx {\varphi _{r = a}} = \left( {\frac{3}{2} - \frac{{{v_0}\varepsilon }}{{\sigma \mathit{\boldsymbol{E}}a}}} \right)\mathit{\boldsymbol{E}}a\cos \theta , $ | (13) |
式中:φr=a+d为r=a+d处电势(V);φr=a为r=a处电势(V);φmetal为金属液滴的电势(V)。
在电解质溶液黏度较大,且金属液滴运动速度较小时,可认为流体的流动是小雷诺数流动的斯托克斯流,可将纳维-斯托克斯方程简化[24]为
| $ {\nabla ^2}\mathit{\boldsymbol{v}} = \frac{1}{\eta }\nabla p, $ | (14) |
式中:η为电解质溶液黏度(Pa·s);p为压强(Pa)。同时还有连续方程
| $ \nabla \cdot \mathit{\boldsymbol{v}} = 0. $ | (15) |
式(14)与式(15)的形式同样满足金属液滴内部的情形。引入流函数ψ,解四阶的欧拉方程,并代入边界条件式(16)至式(22)
| $ \left. {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_r} = - \mathit{\boldsymbol{U}}\cos \theta }\\ {{\mathit{\boldsymbol{v}}_\theta } = \mathit{\boldsymbol{U}}\sin \theta } \end{array}} \right\}r \to \infty . $ | (16) |
式中:U为金属液滴球心相对于无限远处的流体的速度(m/s)。
| $ \left. {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_{r,{\rm{ 溶液 }}}} \ \ = {\mathit{\boldsymbol{v}}_{r,{\rm{ 金属液滴 }}}}\ \ \ \ \ = 0}\\ {{\mathit{\boldsymbol{v}}_{\theta ,{\rm{ 溶液 }}}} \ \ = {\mathit{\boldsymbol{v}}_{\theta ,{\rm{ 金属液滴}}}}} \end{array}} \right\}r = a, $ | (17) |
| $ {\mathit{\boldsymbol{v}}_r},{\mathit{\boldsymbol{v}}_\theta }{\rm{ 在 }}r = 0{\rm{ 处均为有限值}}{\rm{. }} $ | (18) |
在界面处根据应力张量平衡有
| $ \left. {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\tau }}_{rr,{\rm{ 溶液 }}}} \ \ + {\mathit{\boldsymbol{\tau }}_{rr,{\rm{ 界面 }}}} \ \ = {\mathit{\boldsymbol{\tau }}_{rr,{\rm{ 金属液滴 }}}}}\\ {{\mathit{\boldsymbol{\tau }}_{r\theta ,{\rm{ 溶液 }}}} \ \ + {\mathit{\boldsymbol{\tau }}_{r\theta ,{\rm{ 界面 }}}} \ \ = {\mathit{\boldsymbol{\tau }}_{r\theta ,{\rm{ 金属液滴 }}}}} \ \ \ \ \ \end{array}} \right\}r \to a, $ | (19) |
式中:τrr为液滴界面法向应力(Pa),τrθ为液滴界面切向应力(Pa)。其中溶液和金属液滴的应力可根据广义牛顿黏性定律得到
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{\tau }}_{rr,{\rm{ 溶液 }}}} \ \ = - {\mathit{\boldsymbol{p}}_{rr}} + 2\eta \frac{{\partial {\mathit{\boldsymbol{v}}_r}}}{{\partial r}}\\ {\mathit{\boldsymbol{\tau }}_{r\theta ,{\rm{ 溶液 }}}} \ \ = \eta \left( {\frac{1}{r}\frac{{\partial {\mathit{\boldsymbol{v}}_r}}}{{\partial \theta }} + \frac{{\partial {\mathit{\boldsymbol{v}}_\theta }}}{{\partial r}} - \frac{{{\mathit{\boldsymbol{v}}_\theta }}}{r}} \right) \end{array} \right\}, $ | (20) |
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{\tau }}_{rr,{\rm{ 金属液滴}}}} \ \ \ \ \ \ = - {\mathit{\boldsymbol{p}}_{rr}} + 2{\eta ^\prime }\frac{{\partial {\mathit{\boldsymbol{v}}_r}}}{{\partial r}}\\ {\mathit{\boldsymbol{\tau }}_{r\theta ,{\rm{ 金属液滴 }}}}\ \ \ \ \ \ = {\eta ^\prime }\left( {\frac{1}{r}\frac{{\partial {\mathit{\boldsymbol{v}}_r}}}{{\partial \theta }} + \frac{{\partial {\mathit{\boldsymbol{v}}_\theta }}}{{\partial r}} - \frac{{{\mathit{\boldsymbol{v}}_\theta }}}{r}} \right) \end{array} \right\}, $ | (21) |
式中:prr为界面法向压强(Pa);η′为金属液滴黏度(Pa·s);在界面处界面张力产生的法向应力和切向应力可表示为
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{\tau }}_{rr,{\rm{ 界面张力}}}} \ \ \ \ \ \ = \frac{{2\gamma }}{a} = \frac{{2\left( {{\gamma _0} - \varepsilon (\Delta \varphi )} \right)}}{a}\\ {\mathit{\boldsymbol{\tau }}_{r\theta ,{\rm{ 界面张力 }}}}\ \ \ \ \ \ = - \frac{{\partial \gamma }}{{a\partial \theta }} = - \frac{{\varepsilon \partial (\Delta \varphi )}}{{a\partial \theta }} \end{array} \right\}, $ | (22) |
式中Δφ由式(13)代入。根据以上边界条件,解得流场速度方程为
| $ {\mathit{\boldsymbol{v}}_r} = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{U}}\left( {\frac{{{a^3}}}{{{r^3}}} - 1} \right)\cos \theta ,}&{r \ge a}\\ {\frac{{3\mathit{\boldsymbol{U}}}}{2}\left( {1 - \frac{{{r^2}}}{{{a^2}}}} \right)\cos \theta ,}&{r < a} \end{array}} \right., $ | (23) |
| $ {\mathit{\boldsymbol{v}}_\theta } = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{U}}\left( {\frac{{{a^3}}}{{2{r^3}}} + 1} \right)\sin \theta ,}&{r \ge a}\\ {\frac{{3\mathit{\boldsymbol{U}}}}{2}\left( {\frac{{2{r^2}}}{{{a^2}}} - 1} \right)\sin \theta ,}&{r < a} \end{array}} \right., $ | (24) |
将式(23)和式(24)代入式(19)可得
| $ \mathit{\boldsymbol{U}} = \frac{{\varepsilon \mathit{\boldsymbol{E}}a}}{{2\eta + 3{\eta ^\prime } + \frac{{{\varepsilon ^2}}}{\sigma }}}. $ | (25) |
本文研究体系中20 ℃时η′=0.002 4 Pa·s,η>0.5 Pa·s,σ>10 S/m,ε为10-2 C/m2的量级,因此η>>η′,2η>>ε2/σ。式(25)可以简化为
| $ \mathit{\boldsymbol{U}} = \frac{{\varepsilon \mathit{\boldsymbol{E}}a}}{{2\eta }}. $ | (26) |
式(26)为理想化的理论公式,实际中的ε并不容易测得,很有必要采用实验对其进行研究,本文正是基于此目的,对影响电毛细运动速度的各个因素进行实验研究,探索它们的影响规律。
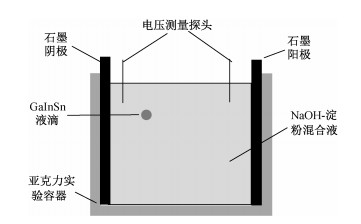
1.2 实验材料及方法使用电子天平称量金属液滴, 称量玉米淀粉和NaOH并制成900 mL的NaOH-淀粉混合液,使用黏度计测量混合液的黏度。如图 4所示,实验采用由亚克力板拼成的长方体容器,内部尺寸为160 mm×5 mm×90 mm,左右各一个尺寸为5 mm×5 mm×100 mm的石墨电极棒。石墨电极连接直流稳压电源并保持电极间距150 mm以形成稳定的电场。电压测量探头在溶液内部相距10 cm,将探头分别连接示波器以记录探头间的实际电势差。将混合液加入到容器中,并接好电路。打开示波器记录溶液内实际电势差,从左上角加入金属液滴,由于密度差液滴自然沉降,当降到一定位置时,开启直流稳压电源,同一实验条件重复进行3次实验,并使用摄像机记录液滴的整个运动过程。
|
Download:
|
| 图 4 实验装置示意图 Fig. 4 Diagram of experimental device | |
以淀粉质量40 g、NaOH质量25 g、液滴质量0.06 g以及电极间施加电压30 V的实验条件为例讲述视频处理过程及结果分析。将视频文件导入到MATLAB中通过提前编写好的程序进行图像识别处理,图 5表示处理过程中得到的每一步的图像,箭头指出的位置为液滴所在位置。先将视频分解为一帧帧的图像, 图 5(a)为其中一帧原始图像。将原始图像转化为灰度图,如图 5(b)。利用金属液滴与周围介质的灰度值不同,编写相应的图像识别程序,经二值化处理,识别金属液滴并将其显现,如图 5(c)。最后利用矩心函数计算液滴的矩心位置,以此代表液滴的位置并记录。图 5(a)中两条短横线代表 1 cm的标度尺。

|
Download:
|
| 图 5 图像处理过程 Fig. 5 Image processing | |
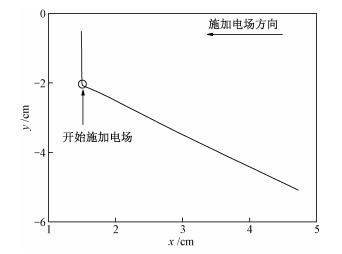
根据所记录每一帧液滴的位置,便可做出图 6所示的金属液滴的电毛细运动轨迹图。从图中可以看出在未施加水平电场时,液滴受重力驱动竖直向下运动,在施加电场后,由于受到溶液水平向右的黏性摩擦力和竖直方向的重力,液滴沿合力方向运动。
|
Download:
|
| 图 6 液滴运动轨迹图 Fig. 6 Trajectory diagram of droplet movement | |
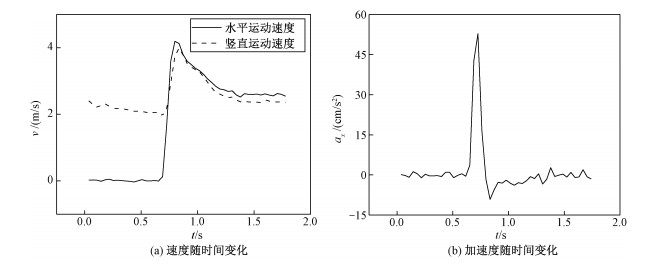
已知两帧图片之间的时间间隔为0.034 s以及每帧图片中液滴的实际位置,由此可计算出液滴的运动速度,如图 7(a)所示。液滴的运动速度随时间的变化率即为液滴的加速度,如图 7(b)所示。图 6中在施加电场位置,液滴的运动轨迹存在一个陡峭的转折点而非一条平滑的曲线,这说明在施加电场的一瞬间液滴的加速度很大,因此水平方向的运动速度迅速增大达到最大值,从图 7中也可以验证这一结论。图 7(a)还可得出尽管液滴水平速度迅速达到最大值,但最大值并不稳定,在到达最大值后水平方向的运动速度又经历了相对于加速阶段较缓慢的减速过程,并最终达到稳定值。在此将水平运动的稳定值定义为通常意义的电毛细运动速度。图 7(a)显示电毛细运动速度比重力沉降速度大,而GaInSn金属液滴密度为NaOH-淀粉混合液密度的6倍左右(GaInSn密度为6 440 kg/cm3,NaOH-淀粉混合液密度稍大于1 000 kg/cm3),这说明电毛细运动驱动的运动效果非常显著。从图 7(a)中还发现在施加电场后重力方向的速度也得到一定程度上的增加,这可能是因为溶液中上下存在一定的电势差。
|
Download:
|
| 图 7 金属液滴运动规律 Fig. 7 The rule of metallic droplet motion | |
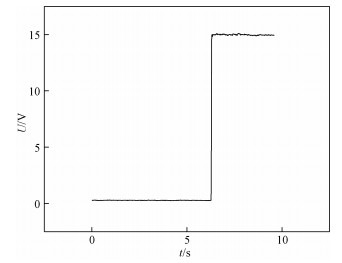
在电极附近会发生电解反应,并产生气泡。但从图 8可以看出在施加电压后,溶液中10 cm距离的电压并不随时间减小,所以图 7(a)中电毛细运动速度减小并不是由于气泡等产生的分压引起的。运动速度先迅速增大后缓慢减小可能是因为液滴在施加电场瞬间处于非稳态,此时液滴还未及时变形,而溶液中的离子已经重新排列,这导致黏性摩擦力在此刻是最大的,因而液滴运动速度迅速达到最大值。此后由于运动过程受到溶液的阻力作用而发生变形,且由于界面处的液体流动较快导致界面过剩电荷密度梯度减小,速度缓慢降低,当液滴达到动态平衡时运动速度趋于稳定。
|
Download:
|
| 图 8 溶液中10 cm距离的电压随时间变化 Fig. 8 The voltage at a distance of 10 cm in solution varies with time | |
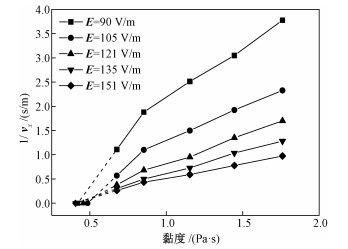
图 9显示不同电场强度下电解质溶液黏度对电毛细运动的影响,其中NaOH浓度为0.69 mol/L,液滴半径为1.31 mm。在黏度介于853~1 760 mPa·s时电毛细运动速度倒数近似是黏度的线性函数,这表明此时电毛细运动速度与黏度成反比。当黏度小于853 mPa·s时电毛细运动速度的倒数随黏度的变化率增大,这表明当黏度较小时电毛细运动速度变化规律不再满足式(26)。图中还可以看出图线的延长线并不交于坐标原点,这是因为在溶液黏度较小的情况下不能忽略式(25)中金属液黏度、电导率和液滴表面过剩电荷密度带来的影响。
|
Download:
|
| 图 9 电解质溶液黏度对电毛细运动速度的影响 Fig. 9 The effect of viscosity of electrolyte solution on the velocity of electrocapillary movement | |
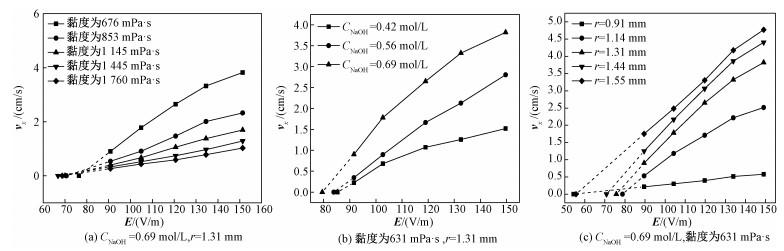
图 10描述不同条件下电场强度对金属液滴电毛细运动速度的影响。图 10(a)~10(c)均表明电毛细运动速度随电场强度增加而增大。图 10(a)和图 10(c)显示电场强度在90~135 V/m时电毛细运动速度与电场强度成线性关系,但当电场强度大于135 V/m时电毛细运动速度随电场强度的增大曲线的斜率有减小的趋势。根据图 2,在电场强度逐渐增加过程中,液滴两端的界面张力关于纵坐标轴向两端扩展。在右端的界面张力变化率逐渐减小,而左端变化率几乎不变的情况下,随电场强度的增加液滴两端界面张力差变化率减小。且当电场强度增大到使得液滴两侧电势差达到分解电压时,就会发生去极化作用,此时表面过剩电荷不会增加甚至会减小,这均会降低电毛细运动速度。
|
Download:
|
| 图 10 电场强度对电毛细运动速度的影响 Fig. 10 The effect of electric field intensity on the velocity of electrocapillary movement | |
从图中可以看出图线的延长线并非交于坐标原点,说明在电场强度降低到一定程度时,电毛细运动速度为零。将图线的延长线与坐标轴的交点的电场强度定义为激发电场强度。由图 10可见,激发电场强度与溶液的黏度、电导率以及液滴半径均有关。图 10(a)说明溶液黏度越小所需要的激发电场强度越大。图 10(b)显示NaOH浓度越大所需要的激发电场强度越小。这是因为溶液中离子浓度越大,表面过剩电荷密度就越大,所以激发电场强度就越小。图 10(c)显示液滴半径越大所需激发电场强度越小,液滴半径越大意味着液滴的表面积也越大,表面过剩电荷密度就越大,液滴受到的界面张力就越大,所以激发电场强度就越小。
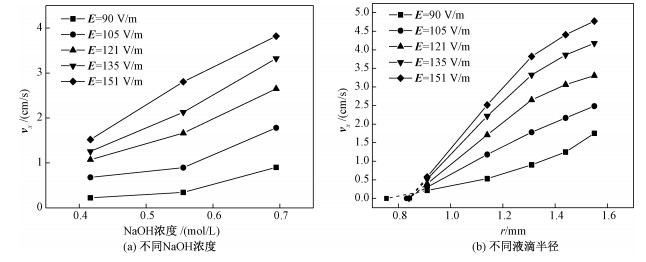
2.3 NaOH浓度和液滴半径分别对电毛细运动的影响图 11(a)显示不同电场强度NaOH浓度对电毛细运动速度的影响,其中溶液的黏度为631 mPa·s,液滴半径为1.31 mm。图中表明电毛细运动速度随NaOH浓度增加而增加,这是因为NaOH浓度增加会导致溶液中离子浓度的增加,进而使液滴界面过剩电荷密度增加。图 11(b)显示不同电场强度下液滴半径对电毛细运动速度的影响,其中溶液黏度为631 mPa·s,NaOH浓度为0.69 mol/L。从图中可以得出当液滴半径在0.91~1.31 mm时,电毛细运动速度与液滴半径成正比。除实验条件为电场强度是90 V/m外,液滴半径大于1.31 mm时电毛细运动速度随液滴半径的增大曲线的斜率有减小的趋势。当液滴半径较大时液滴两侧的电势差大于分解电压,此时发生去极化作用,液滴表面过剩电荷密度不再增加。其次,由图 2可见液滴半径较大时,液滴两端界面张力差变化率随半径增加而减小,在极端情况下界面张力的最大值出现在液滴界面某处,这会完全改变液滴界面附近的流场,大大降低液滴运动速度。图中还可得出图线的延长线不交于坐标原点,说明当液滴半径小于0.8 mm时,电毛细运动速度为零。
|
Download:
|
| 图 11 NaOH浓度和液滴半径对电毛细运动速度的影响 Fig. 11 The effect of NaOH concentration and droplet radius on the velocity of electrocapillary movement | |
本文搭建并研究一个考察电毛细运动速度影响规律的实验。实验结果表明:在施加电场后,电毛细运动速度经历迅速增大到最大值,缓慢减小到稳定值以及维持稳定值不变3个阶段。黏度在853~1 760 mPa·s,电场强度在90~135 V/m或液滴半径在0.91~1.31 mm时液滴运动速度满足电毛细运动公式。当黏度小于853 mPa·s,电场强度大于135 V/m或液滴半径大于1.31 mm时,电毛细运动速度的变化率均会减小。当电场强度小于激发电场强度或液滴半径小于0.8 mm时电毛细运动速度为零。
| [1] |
高兵兵.基于毛细力自驱动的微流控芯片及在POCT中的应用[D].南京: 东南大学, 2017.
|
| [2] |
凌明祥, 陈立国. 基于介电润湿效应的微液滴操控[J]. 压电与声光, 2013, 35(4): 604-608. Doi:10.3969/j.issn.1004-2474.2013.04.035 |
| [3] |
Cho S K, Moon H, Kim C J. Creating, transporting, cutting, and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits[J]. Journal of Microelectromechanical Systems, 2003, 12(1): 70-80. Doi:10.1109/JMEMS.2002.807467 |
| [4] |
戴宇晴.电场驱动下液滴的动力学特性研究[D].河北保定: 华北电力大学, 2017.
|
| [5] |
王静.直流电场作用下油中水滴的破裂机理研究[D].山东青岛: 中国石油大学, 2016.
|
| [6] |
Feng J Q, Scott T C. A computational analysis of electrohydrodynamics of a leaky dielectric drop in an electric field[J]. Journal of Fluid Mechanics, 1996, 311: 289-326. Doi:10.1017/S0022112096002601 |
| [7] |
Mugele F, Baret J C. Electrowetting:from basics to applications[J]. Journal of Physics:Condensed Matter, 2005, 17(28): 705-774. Doi:10.1088/0953-8984/17/28/R01 |
| [8] |
Ichimura K, Oh S K, Nakagawa M. Light-driven motion of liquids on a photoresponsive surface[J]. Science, 2000, 288(5471): 1624-1626. Doi:10.1126/science.288.5471.1624 |
| [9] |
寻波, 胡文瑞. 多热源分布时薄层液体中热毛细对流的分叉特征[J]. 中国科学院研究生院学报, 2005, 22(6): 733-738. Doi:10.3969/j.issn.1002-1175.2005.06.012 |
| [10] |
陈然, 王增辉, 倪明玖. 强磁场对导电流体热毛细流动和换热影响的实验研究[J]. 中国科学院大学学报, 2019, 36(1): 25-30. |
| [11] |
李长荣, 江明丽. FeO-CaO-SiO2熔渣中金属铜滴的电毛细迁移[J]. 中国有色冶金, 2010, 39(3): 63-66. |
| [12] |
李秋菊, 陈鹏, 林姜多, 等. 铜滴在富FeO熔渣中的电迁移行为[J]. 材料与冶金学报, 2010, 9(1): 28-30. |
| [13] |
Itoh S, Choo R T C, Toguri J M. Electrocapillary motion of copper and nickel matte droplets on fayalite-based slag surfaces[J]. Canadian Metallurgical Quarterly, 1995, 34(4): 319-330. Doi:10.1179/cmq.1995.34.4.319 |
| [14] |
Zhang H W, Shi X Y, Zhang B. Behaviors of the molten copper slag in the vertical electric field[J]. ISIJ International, 2013, 53(10): 1704-1708. Doi:10.2355/isijinternational.53.1704 |
| [15] |
Warczok A, Riveros G. Slag cleaning in crossed electric and magnetic fields[J]. Minerals Engineering, 2006, 20(1): 34-43. |
| [16] |
张家雯, 郭培民, 杨海森, 等. 电渣重熔体系电毛细振荡的动态模拟[J]. 钢铁研究学报, 2000, 12(5): 10-12. |
| [17] |
张国堤.液态Ga-In合金及Wood合金在NaOH水溶液中的电毛细行为[D].兰州: 兰州理工大学, 2017.
|
| [18] |
Choo R T C, Toguri J M. The electrodynamic behavior of metal and metal sulphide droplets in slags[J]. Canadian Metallurgical Quarterly, 1992, 31(2): 113-126. |
| [19] |
Soffer A. Electrocapillary equations and double-layer charge of reversible electrodes[J]. Journal of Electroanalytical Chemistry, 1972, 40(1): 153-165. |
| [20] |
Wang M F, Jin M J, Jin X J, et al. Modeling of movement of liquid metal droplets driven by an electric field[J]. Physical Chemistry Chemical Physics, 2017, 19(28): 18505-18513. |
| [21] |
Handschuh-Wang S, Chen Y, Zhu L, et al. Electric actuation of liquid metal droplets in acidified aqueous electrolyte[J]. Langmuir, 2018, 35(2): 372-381. |
| [22] |
Warczok A, Utigard T A. Settling of copper drops in molten slags[J]. Metallurgical and Materials Transactions B, 1995, 26(1): 1165-1173. |
| [23] |
时宝国. 匀强电场中导体球表面感应电荷的分布规律[J]. 红河学院学报, 2007, 5(2): 80-82. |
| [24] |
倪玲英.复杂通道中油滴的运动规律与颗粒周围剪切力场研[D].山东青岛: 中国石油大学, 2008.
|
 2021, Vol. 38
2021, Vol. 38 


