当高功率飞秒脉冲在透明介质中传输时，会由于克尔自聚焦和电离产生电子的散焦效应之间的动态平衡而产生细丝状结构。飞秒激光形成的细丝具有较高光强，并且电离产生低密度的等离子体，同时产生能够覆盖可见光和近红外的超连续光谱^[1]。该超连续光谱具有高亮度、宽光谱、良好的时间相干和空间相干性，并且具有超短的脉宽。由于这些独特的性质，超连续光谱在遥感探测^[2]、医学成像^[3]以及单周期脉冲产生^[4]等方面有着重要应用，因而备受关注。

透明介质中的超连续光谱是由于自相位调制、电离和自陡峭效应的共同作用而产生的。这些非线性效应与透明介质的光学性质紧密相关。固体介质有较高的非线性系数，所以固体介质中产生的超连续光谱转化效率较高，其中以熔融石英最为常见。飞秒脉冲在熔融石英中产生超连续光谱的特征非常敏感地依赖于激光的初始条件。飞秒脉冲激光的空间强度分布^[5]、相位分布^[6]、脉冲波形^[7]、初始功率^[8]以及中心波长^[9-10]等参数的改变都会引起成丝过程飞秒脉冲时空演化的不同，进而引起超连续光谱特征的改变。由于超连续光谱的众多应用，需要控制和优化超连续光谱的特征，比如控制展宽范围和光谱强度以适应不同应用的需求。脉宽是飞秒脉冲的重要参数，不同脉宽的飞秒脉冲成丝演化过程会有很大不同。当飞秒脉冲具有不同啁啾和脉宽时，成丝的起点和长度展现出极大的不同^[11]，并且成丝产生的等离子体密度也发生较大的改变^[12]。因此，飞秒脉冲成丝产生的超连续光谱也会因为脉冲初始脉宽的不同而具有不同的光谱特征。Calendron等^[13]研究皮秒量级脉冲脉宽对超连续光谱展宽的影响。但飞秒和皮秒脉冲在固体介质中成丝传输的电离机制不同^[12]，脉冲时空演化必然会不一样，所以飞秒脉冲脉宽对固体介质中产生的超连续光谱特征的影响还不清楚。

本文模拟不同脉宽的飞秒脉冲在熔融石英中成丝并产生超连续辐射的过程。计算3种情况下不同脉宽的脉冲，包括初始光谱宽度不同的无啁啾脉冲和具有正负啁啾且初始光谱宽度相同的脉冲。

1 飞秒脉冲在熔融石英中传输的方程及计算参数

飞秒激光脉冲在熔融石英中的非线性传输可以由脉冲包络时空演化的非线性薛定谔方程和电离产生电子的密度方程来描述^[14]。该耦合方程写成如下形式：

$ \begin{aligned} \partial_{z} E=& \frac{\mathrm{i}}{2 k_{0}} T^{-1} \nabla_{\perp} E+\mathrm{i} D E+\\ & \mathrm{i} \frac{\omega_{0}}{c} n_{2} T \int\limits_{-\infty}^{t} R\left(t-t^{'}\right)\left|E\left(t^{'}\right)\right|^{2} \mathrm{~d} t^{'} E-\\ & \mathrm{i} \frac{k_{0}}{2 n_{0} \rho_{\mathrm{c}}} T^{-1} \rho E-\frac{\beta^{(\kappa)}}{2}|E|^{2 \kappa-2} E-\frac{\sigma}{2} \rho E, \end{aligned} $

(1)

$ \frac{\partial \rho }{\partial t}=\frac{{{\beta }^{(\kappa )}}{{\left| E \right|}^{2\kappa }}}{{{U}_{i}}{{\rho }_{\text{at}}}}({{\rho }_{\text{at}}}-\rho )+\frac{\sigma \rho I}{{{U}_{i}}}-\frac{\rho }{{{\tau }_{\text{rec}}}}. $

(2)

式中：E是飞秒激光脉冲的电场包络; z是激光脉冲在熔融石英中传输的距离; 飞秒脉冲的中心波长λ₀=800 nm，k₀=2π/λ₀是激光的中心波数; ω₀是激光的中心频率。方程(1)右侧各项依次为衍射，色散，克尔效应(瞬时项和延时项)，电子散焦，多光子电离耗散和碰撞电离耗散项。算符$T=1+\frac{\text{i}}{{{\omega }_{0}}}{{\partial }_{t}}$在衍射项前面描述脉冲时空聚焦效应，在克尔效应前描述自陡峭效应。方程(2)右侧依次为多光子电离项，碰撞电离项和电子复合项。方程中各参数依次为：克尔系数n₂=3.2×10^-16 cm²/W，多光子电离系数β^(κ)=8.4×10^-67 cm⁹/W⁵，光子数κ=6，逆布里渊散射截面σ=6.57×10^-19。描述色散项的算符$D={{\sum }_{n\ge 2}}(\frac{{{k}^{(n)}}}{n!}){{(\text{i}{{\partial }_{t}})}^{n}}$，色散系数k⁽ⁿ⁾=∂ⁿk/∂ωⁿ|_ω0，其中波数k=n(ω)ω/c由熔融石英的色散方程计算得到^[15]。描述熔融石英中克尔效应的响应函数$\mathscr{R}\left(t-t' \right)=\left(1-f \right)\delta \left(t-t' \right)+f\theta \left(t-t' \right)$ $\frac{1+\omega _{\text{R}}^{2}\tau _{\text{R}}^{2}}{{{\omega }_{\text{R}}}\tau _{\text{R}}^{2}}{{\text{e}}^{-\frac{t-t' }{{{\tau }_{\text{R}}}}}}\text{sin}({{\omega }_{\text{R}}}\left(t-t' \right))$，延时效应所占比例为f=0.18，分子振动延迟时间τ_R=32 fs，共振频率ω_R=0.082 fs^-1。临界等离子体密度ρ_c=1.73×10²¹ cm^-3，ρ_at是中性原子密度^[14]，电子复合时间τ_rec=150 fs。

初始位置的飞秒脉冲的电场包络写为

$ E={{E}_{0}}{{\text{e}}^{-({{x}^{2}}/w_{0}^{2}+{{y}^{2}}/w_{0}^{2})}}{{\text{e}}^{-{{t}^{2}}/\tau _{0}^{2}}}{{\text{e}}^{-\text{i}C{{t}^{2}}/\tau _{0}^{2}}}\cdot {{\text{e}}^{-\text{i}{{k}_{0}}{{r}^{2}}/2f}}, $

(3)

式中:w₀是激光初始光腰半径，τ₀是初始脉宽，f是聚焦透镜焦距，C是啁啾参数，w₀=42 μm，f=0.1 m。对于不同的脉宽激光初始能量保持不变，为0.8 μJ。

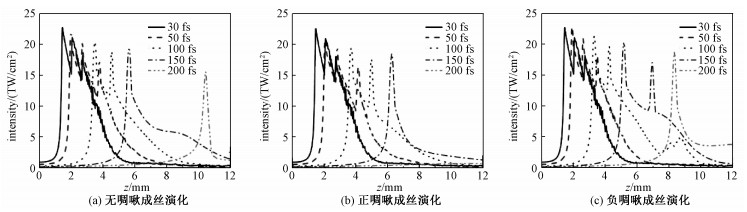
2 不同脉宽的飞秒脉冲在熔融石英中的成丝及超连续辐射

分别模拟计算无啁啾、正啁啾和负啁啾3种情况下不同脉宽的飞秒脉冲在熔融石英中传输成丝并产生超连续辐射的过程。首先，得到飞秒脉冲的峰值光强随传输距离的演化，如图 1所示。在无啁啾的情况下，从图 1(a)可以看出，脉宽为30 fs的脉冲成丝最早，z=1.37 mm可以认为是其成丝的起始位置(按强度达到10 TW/cm²计算)，之后在1.48 mm处形成第1个强度峰，最大光强为22.7 TW/cm²。随着脉宽的增加，成丝位置逐渐推迟，这是由于脉冲初始脉宽越大，峰值功率降低，按照移动聚焦模型，成丝起点越远，细丝的最大光强也逐渐减小，50 fs脉冲成丝的最大光强是21.9 TW/cm²，而200 fs脉冲产生的最大光强是15.5 TW/cm²。另一方面，成丝长度也随着脉宽的增加而逐渐减小。

对于带有正啁啾或负啁啾的飞秒脉冲，脉宽对细丝演化的影响与无啁啾时的情况类似，即随着脉宽增加，成丝起点延后，最大光强降低，长度也逐渐缩短，如图 1(b)和1(c)所示，但是又表现出不一样的特点。对于同一脉宽，带有正啁啾的脉冲成丝起点均比无啁啾和负啁啾的情况延后，特别是当脉宽增加到200 fs时，正啁啾脉冲没有成丝。另一方面，对于负啁啾脉冲，在相同脉宽下，其成丝起点均比无啁啾和正啁啾的情况提前。也就是说，在相同的脉宽情况下，与无啁啾脉冲的成丝相比，带有负啁啾脉冲的成丝起点提前，带有正啁啾的成丝起点延后，各种脉冲的成丝位置见表 1。这是由于800 nm的飞秒脉冲处于熔融石英的正色散区域，正色散会引起初始负啁啾的脉冲存在一个脉冲压缩的过程，引起正啁啾脉冲进一步展宽，所以相同脉宽条件下，负啁啾脉冲成丝最早，正啁啾脉冲成丝最晚。脉宽越大，成丝起点随啁啾变化越明显。对于同一脉宽不同啁啾的脉冲，成丝产生的最大光强也不相同。对于50 fs的脉宽，正啁啾、无啁啾和负啁啾的脉冲成丝产生的最大光强分别为21、21.9、22.8 TW/cm²。负啁啾脉冲由于存在脉冲压缩过程，所产生的最大光强最大，无啁啾的次之，正啁啾的最小。

以上结果表明，由于初始脉宽不同，啁啾不同，飞秒脉冲成丝特征有很大不同，因此产生的超连续辐射的特征也必然会不同。为研究脉宽、脉冲啁啾以及初始光谱对超连续辐射的影响，我们计算了以上几种情况的脉冲成丝后产生的超连续光谱。图 2给出上述几种脉冲在传输距离z=15 mm处的光谱。可以看出，对于3种啁啾下脉冲成丝产生的超连续辐射，随着脉宽的增加，蓝移截止波长(定义为归一化强度值等于10^-4处的波长)逐渐增大，光谱的强度也明显减小。首先，对于30、50和200 fs的无啁啾脉冲，成丝以后产生的光谱蓝移截止波长分别是338、345和407 nm，如图 2(a)所示。并且在可见光范围内，30 fs的无啁啾脉冲的光谱强度比150 fs的光谱强度高1个数量级，比200 fs的光谱强度高近2个数量级。由此可见，初始脉宽对于超连续光谱的蓝移截止频率和光谱强度都有很大的影响。对于具有啁啾的脉冲产生的超连续光谱，当脉宽较短时，对比具有正负啁啾的50和100 fs两种情况可以发现，无论是截止频率还是光谱强度差别都不大。对于脉宽较大的脉冲，正负啁啾脉冲开始出现明显差异。当脉宽为150 fs时，正负啁啾脉冲产生的蓝移截止波长十分接近，但负啁啾脉冲产生的光谱强度在蓝移部分比正啁啾产生的要大得多。当脉宽继续增加到200 fs时，正啁啾脉冲没有成丝，因而光谱没有明显展宽，而负啁啾脉冲则产生明显的蓝移。所以对于比较大的脉宽，脉冲初始啁啾对光谱强度影响更为明显。

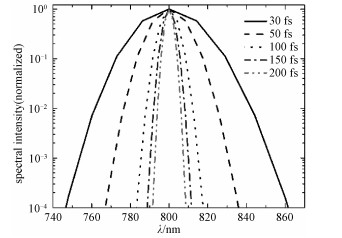
由图 2还发现，当脉宽为50 fs时，无啁啾与正负啁啾脉冲产生的光谱没有明显区别，但是对于100和150 fs的脉冲，无啁啾脉冲产生的光谱在350~600 nm光谱范围内的强度都明显低于正负啁啾情况下的光谱强度。另外，200 fs的无啁啾脉冲产生的光谱强度在这个范围内也明显低于负啁啾的。出现该现象的原因，应该与初始光谱的宽度有关。图 3给出无啁啾的具有不同脉宽脉冲的光谱，其中，30 fs脉冲的光谱宽度最大，其半高全宽为33 nm，脉冲脉宽越大，初始光谱的宽度越小。而正负啁啾脉冲的光谱都与无啁啾的30 fs脉冲的光谱一样，都是33 nm(半高全宽)，所以对于较大脉宽的无啁啾脉冲，其光谱宽度都会小于带有啁啾的脉冲，从而产生的超连续光谱强度也会低于啁啾脉冲的。所以，当脉宽较大时，初始光谱宽度也影响超连续光谱的强度。

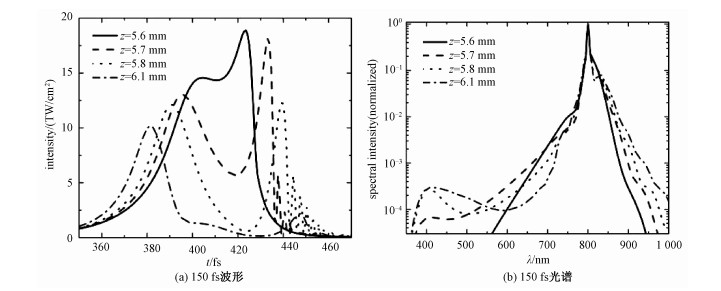
为进一步理解初始脉宽对飞秒激光在熔融石英中成丝及产生超连续光谱的影响，图 4、图 5给出无啁啾30和150 fs两个脉冲传输过程中几个典型传输距离处的脉冲波形分布和光谱分布。对于30 fs脉冲，结合图 4(a)和4(b)可以看到，当传输到z=1.5 mm处时，光强已超过20 TW/cm²，这时脉冲后沿开始变得陡峭，相应地，光谱发生明显的展宽。当脉冲继续传输到z=2.1 mm处时，光强仍然很高，后沿也十分陡峭，光谱蓝移更为明显，截止波长已经达到350 nm附近，短波部分的强度也显著提高。当脉冲传输到z=2.7和3.0 mm时，脉冲光强降低，尽管由于脉冲劈裂产生了许多子脉冲，但光谱强度提高有限。因此对30 fs脉冲产生的超连续光谱影响较大的是在最大光强较强的一段传输距离内。对于无啁啾150 fs脉冲，对光谱展宽影响比较明显的是z=5.6~5.7 mm这段传输距离内，这段距离内脉冲最大光强超过15 TW/cm²。而在z=5.8~6.1 mm这段距离内，光强较低，蓝移光谱强度仅有少许提高。由此可见，光谱的展宽及截止波长都十分依赖于成丝的强度。由于30 fs脉冲产生的细丝以更大的光强传输了更长的距离，因此，其产生的超连续光谱比脉宽大的脉冲的光谱截止波长更短，光谱也更强。

3 结论

本文理论研究不同脉宽的飞秒脉冲在熔融石英中成丝及产生超连续辐射的过程。发现，对于同样的能量，无论是无啁啾还是正负啁啾的飞秒脉冲，脉宽越大，产生的超连续辐射蓝移截止波长越长，蓝移光谱强度越低。进一步研究发现，这主要是因为能量相同，脉宽越大，初始功率越低，形成的细丝不能以较高光强维持较长的传输距离。此外，正负啁啾对较大脉宽的脉冲产生的细丝特征和超连续光谱影响比较明显，适当的负啁啾更有利于脉冲的成丝传输和超连续辐射的增强。