经过2007—2010年的金融危机和2009—2012年的欧债危机,越来越多的学者开始重视极端事件和尾部相关的研究。尾部相关的增加可能是由于线性相关性(当皮尔逊相关系数不等于0时),也可能是由于一些非线性相关性引起的。关于尾部相关性的度量,学术研究涉及较多,但是对于其中的线性相关性和非线性相关性分解的研究并不多见。Poon等[1]提出,相比于线性不相关的投资组合,非线性相关的证券投资组合有着更厚的尾部分布。因此投资决策不仅取决于投资者的风险偏好,也取决于投资者对线性和非线性风险的偏好。
经典统计学通过线性相关系数刻画相关性,然而非线性相关在金融研究中十分常见,并且往往在危机时快速上升,引发严重后果。一般情况可以通过Granger因果检验对非线性相关关系进行研究,但由于无法对相关性的强弱给出准确的度量,不能适用于一些定量的风控模型。
近些年的研究中,学者更加关注相关系数的动态变化,DCC-GARCH是一种常用的研究动态线性相关系数的模型。DCC-GARCH模型从ARCH模型等一步步发展过来,Engle[2]提出ARCH模型,对时间序列的条件方差进行建模,历史的随机扰动项和当前的条件方差符合函数关系,这一模型对普遍存在异方差的金融时间序列建模效果较好。Bollerslev[3]在此基础上提出更一般的GARCH模型,GARCH模型中的条件方差是过去条件方差和随机扰动项的函数。随后Engle[4]提出DCC-GARCH模型,简化随时间变动的条件协方差矩阵的计算方法,并且得到不同变量之间动态时变的相关系数。
在尾部相关性的研究中,一个经常使用的方法是使用Copula模型和极值理论。该方法主要分为两步,第1步是假设分布的尾部渐近收敛速度为指数形式(边缘分布和联合分布都要满足),第2步是使用极值Copula模型。Copula函数不限定边缘分布的形式,可以将用于反映相依关系的Copula函数和边缘分布分开研究,并可以研究变量之间的非线性、非对称的相关关系。Embrechts等[5]将Copula模型引入金融领域,迅速得到应用。Patton[6]构建动态Copula模型,基于ARMA模型的思想,假定Copula模型中的参数满足类似ARMA模型的演化形式。Rodríguez等[7]使用Copula模型,对各国股票市场指数之间的相关性进行研究。Copula模型虽然有以上诸多优点,但依然需要认识到它的局限性,Straetmans等[8]指出Copula在构建模型的时候需要假定变量服从于某种未知的分布,并且在估计时依赖对这个分布的参数估计,这不可避免地需要进行复杂的最优化,并且有些情形难以计算,造成一定的局限性。国内也有很多学者对尾部相关性的理论和应用进行研究。史道济和关静[9]利用Logistic条件模型和GEV条件模型分析1992—1999年沪深股市日内收盘价的对数利润数据。韦艳华和张世英[10]建立Copula-GARCH模型,对上海证券交易所各种指数收益率进行条件相关性研究。张明恒[11]利用Copula联结函数、混合分布和Jacob矩阵,构造多金融资产风险价值的Copula计量方法。
Ricci和Veredas[12]提出TailCoR模型,提供了研究尾部相关关系的一个新思路。TailCoR模型解决了Copula模型的一些局限性,比如不依赖于特定的分布,不需要最优化,在小样本下的性质表现良好。除刻画尾部相关性外,TailCoR模型在椭圆分布的假定下,可以直接将模型中的尾部相关系数分解成线性和非线性两部分(线性部分和非线性部分两个因式的乘积组成完整的尾部相关系数),这有利于分析尾部相关性变化的原因,比如分析尾部相关性增加是由线性还是非线性相关性的上升引起的。文献[12]基于TailCoR模型分析美国和欧洲的大型商业银行股价收益率的尾部相关性,发现尾部相关性在2008年金融危机和欧债危机期间上升,更具体地,在2008年金融危机期间,线性和非线性相关性都有所上升,而在欧债危机期间,主要是非线性相关性的上升导致整体尾部相关性的上升。Geraci等[13]则基于TailCoR模型,研究卖空与股价变动的相关性。
TailCoR模型假定尾部相关系数是静态的,不随时间变化。要想观察TailCoR的动态变化,可以基于滑窗(比如一个季度)的方法进行刻画,在每个窗宽内得到一个TailCoR值,观察其随时间的变化趋势。由于TailCoR计算过程中,需要计算样本分位数,这就导致窗宽不能取得过短,因此基于滑窗的TailCoR模型对尾部相关性的刻画就不是很准确,而动态TailCoR模型可以解决这个问题。目前还没有学者基于TailCoR模型研究国内金融资产的尾部相关性。本文以TailCoR模型为基础,构建动态TailCoR模型,并进一步将尾部相关性分解成动态线性和非线性成分。在实证研究中,分别使用静态TailCoR模型和改进后的动态TailCoR模型,研究国内4家银行股价收益率之间的相关性,并分析尾部相关性随时间的变化趋势。
1 动态TailCoR模型的构建与尾部相关性的度量 1.1 TailCoR模型在介绍TailCoR具体的计算公式之前,首先对TailCoR进行直观的解释。假设随机变量Xj和Xk在标准化后皮尔逊相关系数为正,那么点(Xj, Xk)出现在第1和第3象限的概率更高。存在一条穿过原点的直线θ=π/4,将所有的样本点投影到这条直线上,产生一个新的随机变量Zjk。直观理解,当两个随机变量正相关性很强,投影点会分散在整条直线上。而如果两个随机变量相关性不强,则投影点会集中在0附近。因此,可以用Zjk的上分位数和下分位数的差刻画两个随机变量的相关性强弱。
另外Zjk的上下分位数的差与尾部相关性也有关系。因为原点附近的数据对于分位数差没有影响,而尾部的数据对于分位数的差却有重要影响。图 1将上述过程展现在坐标系中,下面给出TailCoR模型的具体构建过程。

|
Download:
|
| 图 1 TailCoR模型图示 Fig. 1 Diagrammatic representation of TailCoR | |
假设Xt, t=1, 2, …, T是随机向量,维度是N,Xjt和Xkt是其中两个分量,下面给出Xjt和Xkt的尾部相关的度量过程。首先将Xjt进行处理,得到
| $ {Y_{jt}} = \frac{{{X_{jt}} - Q_{0.5}^j}}{{{\rm{IQR}}_\xi ^j}}, $ | (1) |
其中:Qξj是Xjt的ξ分位数,IQR表示分位数离差,即IQRξj=Qξj-Q1-ξj,通常可以选ξ=0.75和ξ=0.25的分位点对数据进行处理。同样可以对Xkt进行处理,得到Ykt。
将(Yjt, Ykt)在直线θ=φ上投影,得到一个新的随机变量
| $ Z_t^{jk} = {Y_{jt}}\cos \varphi + {Y_{kt}}\sin \varphi . $ | (2) |
Ztjk的分位数离差定义为
| $ {\rm{IQR}}_\tau ^{jk} = Q_\tau ^{jk} - Q_{1 - \tau }^{jk}, $ | (3) |
其中:Qτjk是Ztjk的τ分位数,τ代表对尾部的定义(超过τ和1-τ分位点的样本处于极端状况)。
于是TailCoR定义如下
| $ {\rm{ TailCoR }}_\tau ^{jk}: = {w_g}(\tau ,\xi ){\rm{ IQR }}_\tau ^{jk}{\rm{ , }} $ | (4) |
其中wg(τ, ξ)是一个系数,使得在Xjt和Xkt两个随机变量独立的情况下,TailCoRτjk等于1。
关于TailCoR模型,有如下几个性质:
1) 由定义得到,当Xjt和Xkt相互独立且服从正态分布时,wg(τ, ξ)是IQRτjk的倒数。通过该方法可以得到不同参数(τ, ξ)下的wg(τ, ξ)。文献[12]给出了常用的wg(τ, ξ)表。
2) 类似于皮尔逊相关系数,输入两个离散时间序列样本,可以得到一个TailCoR数值,表示尾部相关性。值得注意的是,TailCoR并不在[-1, 1]之间,当然也不以0为中心。实际上,由式(4)计算出的TailCoR大于1,且呈倒钟型分布。文献[12]基于蒙特卡洛模拟给出了TailCoR在不同分布下的形状。
3) 如果Xjt和Xkt服从椭圆分布(概率等值线是椭圆形状,椭圆分布十分广泛,多元正态分布、多元学生t分布、多元指数分布等都是椭圆分布),那么TailCoR有一些性质,文献[12]进行了严格的证明,下面仅给出结论。
首先,在椭圆分布的假定下,可以证明Xjt和Xkt正相关时,最佳投影线是第1象限角平分线θ=π/4,负相关时为θ=3π/4。
其次,TailCoR可以分解成线性和非线性两部分,如下:
| $ {\rm{ TailCoR }}_\tau ^{jk} = {w_g}(\tau ,\xi )w(\tau ,\xi ,\alpha )\sqrt {1 + \mid {\rho _{jk}}\mid } . $ | (5) |
具体证明过程见文献[12]。
TailCoR可以看成两个因式相乘,其中一个因式是
容易看出TailCoR模型有以下几个优点。第一,TailCoR计算过程简单,不涉及复杂的方程求解和最优化;第二,在椭圆分布的假定下,TailCoR可以分解为线性和非线性两部分,便于分析TailCoR变化是线性相关性上升导致的还是非线性相关性导致的;第三,模型并没有假定原数据的分布情况,适用面更广。
在TailCoR模型的计算过程中,需要对式(3)中取投影后的随机变量Ztjk的分位数进行计算。如果基于分位数回归模型对分位数进行估计,则分位数仍然随着外生解释变量而变化,由此可以得到动态TailCoR的估计。
1.2 非参数分位点回归模型为了对TailCoR进行动态建模,需要基于非参数分位点回归模型对分位点进行动态估计。假定解释变量是一维,被解释变量和解释变量之间满足下面的方程
| $ {Y_i} = g\left( {{X_i}} \right) + {u_{\xi i}}, $ | (6) |
其中g(·)是待估函数,同时Qξ(uξi|X)=0,即uξi的条件分位点是0。于是Y的分位点和解释变量之间满足如下关系
| $ {Q_\xi }(Y\mid X = x) = g(x). $ | (7) |
通过局部常数分位点回归模型,可以得到分位点的估计。给定X=x,最小化下式可以得到参数a的估计:
| $ \hat a = {\min _a}\left\{ {\sum\nolimits_{i = 1}^n {{\rho _\xi }} \left( {{Y_i} - a} \right){K_h}\left( {{X_i} - x} \right)} \right\}, $ | (8) |
其中ρξ(u)=u·(ξ-I(u < 0))。
最小化式(8)所得到的a与解释变量X=x相关,记为
将式(2)中的Ztjk作为被解释变量,引入外生变量Rt作为解释变量,进行非参数分位数回归
| $ {Z_t^{jk} = {g_1}\left( {{R_t}} \right) + {u_\tau },} $ | (9) |
| $ {Z_t^{jk} = {g_2}\left( {{R_t}} \right) + {u_{1 - \tau }}.} $ | (10) |
其中:Qτ(uτ|Rt)=0,Q1-τ(u1-τ|Rt)=0,即对应的条件分位数是0。
基于非参数分位数回归模型可以得到分位数的非参数估计
| $ {\hat Q_\tau ^{jk}\left( {Z_t^{jk}} \right) = {{\hat g}_1}\left( {{R_t}} \right),} $ | (11) |
| $ {\hat Q_{1 - \tau }^{jk}\left( {Z_t^{jk}} \right) = {{\hat g}_2}\left( {{R_t}} \right).} $ | (12) |
以上述分位数的估计替代式(3),便可以得到动态TailCoR模型的估计
| $ {{\rm{IQR}}_\tau ^{jk}\left( {{R_t}} \right) = {{\hat g}_1}\left( {{R_t}} \right) - {{\hat g}_2}\left( {{R_t}} \right),} $ | (13) |
| $ {{\mathop{\rm TailCoR}\nolimits} _\tau ^{jk}\left( {{R_t}} \right) = {w_g}(\tau ,\xi ){\mathop{\rm IQR}\nolimits} _\tau ^{jk}\left( {{R_t}} \right).} $ | (14) |
在文献[12]提出的TailCoR模型中,基于椭圆分布的假设,将TailCoR分解成线性和非线性两部分,并在实证研究中发现TailCoR每次增加的原因是不同的,既可能是由于线性相关性增加而导致,也可能是非线性相关性增加而导致。为了使得动态TailCoR模型也能够进行类似分析,需要对动态TailCoR进行分解。
动态TailCoR模型可以依照式(5)进行分解,需要计算出线性和非线性相关性其中一个。Engle等[4]提出DCC-GARCH模型,简化了随时间变动的条件协方差矩阵的估计方法,并且得到了不同变量之间动态时变相关系数。基于DCC-GARCH模型可以得到动态线性相关系数的估计,进而得到动态非线性相关系数,下面给出具体的过程。
假定有k个资产,信息假定为独立同分布的白噪声过程,服从均值为0、协方差矩阵为Ht的多元正态分布,模型设定如下:
| $ {{r_t} = {\mu _t} + {e_t},} $ | (15) |
| $ {{e_t}\mid {\Omega _t} \backsim N\left( {{\mathit{\boldsymbol{0}}},{\mathit{\boldsymbol{H}}_t}} \right),} $ | (16) |
| $ {{\mathit{\boldsymbol{H}}_t} = {\mathit{\boldsymbol{D}}_t}{\mathit{\boldsymbol{R}}_t}\mathit{\boldsymbol{D}}_t^\prime .} $ | (17) |
其中:rt为资产收益率;Ωt为到t-1时刻的信息集;Dt从单变量GARCH模型中得到,得到条件标准差后取对角元素形成的对角矩阵就是Dt;Rt为动态条件相关系数矩阵,其结构为
| $ {\mathit{\boldsymbol{R}}_t} = {\left( {\mathit{\boldsymbol{Q}}_t^*} \right)^{ - 1}}{\mathit{\boldsymbol{Q}}_t}{\left( {\mathit{\boldsymbol{Q}}_t^*} \right)^{ - 1}}, $ | (18) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_t} = \left( {1 - \sum\limits_{m = 1}^M {{\alpha _m}} - \sum\limits_{n = 1}^N {{\mathit{\boldsymbol{\beta }}_n}} } \right)\mathit{\boldsymbol{\bar Q}} + }\\ {\sum\nolimits_{m = 1}^M {{\alpha _m}} \left( {{\varepsilon _{t - m}}\varepsilon _{t - m}^\prime } \right) + \sum\limits_{n = 1}^N {{\beta _n}} {\mathit{\boldsymbol{Q}}_{t - n}}.} \end{array} $ | (19) |
其中:Qt*为Qt对角线上的数组成的矩阵, Q为标准残差的无条件方差矩阵。
DCC-GARCH模型可以通过两步来估计:第1步,估计每一个资产的单变量GARCH模型的参数;第2步,使用第1步中的标准化残差来估计动态条件相关系数。基于DCC-GARCH模型估计出相关系数矩阵
| $ w(\tau ,\xi ,\alpha ,t) = \frac{{{\mathop{\rm IQR}\nolimits} _\tau ^{jk}\left( {{S_t}} \right)}}{{\sqrt {1 + \left| {{{\hat \rho }_{jk,t}}} \right|} }}. $ | (20) |
以上对动态TailCoR模型进行介绍,同时给出分解后的动态线性相关系数和动态非线性相关系数,下面将该模型用于实证研究。
2 实证研究 2.1 数据和描述性分析银行业务同质性较强,危机期间走势更加趋同,本文对银行股价收益率的相关性进行研究。样本方面,选择工商银行、中国银行、建设银行和招商银行,样本时间段为2008年1月2日到2018年6月29日(共2 553 d)。
本文希望观察尾部相关性在极端行情下的变化,所以希望样本覆盖较长区间,农业银行上市时间较晚,并不符合这一条件。选择招商银行的原因,除上市时间较长以外,股份制银行和4大行在业务模式、投资者类型等方面存在区别,有必要研究在极端市场环境下,股份制银行与4大行股价之间相关性如何变化。
在研究动态TailCoR模型时,本文引入上证综合指数的月度历史波动率作为解释变量,具体计算方法将在动态TailCoR的计算中进行介绍。
按照以下步骤进行实证研究:首先,进行描述性统计;其次,计算整个样本范围内的静态TailCoR以及相应的线性和非线性部分;再次,计算分段TailCoR,窗口宽度设定为半年,计算每个时间段的TailCoR及其线性和非线性部分,观察尾部相关性随时间的变化;最后,使用实际波动率作为外生变量计算出动态TailCoR,基于椭圆分布下的分解,先使用DCC-GARCH模型获得动态线性相关性系数,后获得动态非线性尾部相关性系数。
首先,对4家银行收益率进行描述性统计,并判断是否服从正态分布,结果见表 1。
|
|
表 1 4家银行收益率的描述性统计量和SW检验 Table 1 Descriptive statistics and SW test of the yields of the four banks |
从表 1可以看出,招商银行收益率的标准差高于另外3家大型国有商业银行,股价波动性更高。且4家银行的收益率序列的峰度大于3,偏度大于0,显示出尖峰和右偏的特点。在SW检验的结果中,4个银行的p值均小于0.01,因此4个银行的收益率并不服从正态分布。后面将基于TailCoR模型测量和分析4个银行的尾部相关性。
2.2 4家银行间的静态TailCoR根据上文中TailCoR的定义,容易得到静态TailCoR的计算步骤。在相关系数的估计方面,我们有所调整。Lindskog等[14]利用椭圆分布的几何性质,得出Kendall相关系数在椭圆分布族下不变。因此用样本Kendall相关系数来估计,结果稳健,公式如下
| $ {\hat \rho _{jk}} = \sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2}{{\hat \kappa }_{jk}}} \right), $ | (21) |
其中,
下面给出静态TailCoR的计算步骤,以及线性和非线性部分的分解,计算过程如下:
第1步,对Xjt和Xkt进行标准化,然后得到投影点Ztjk,并计算投影点的分位点差
第2步,选择适当的系数wg(τ, ξ),计算出
| $ \widehat {{\rm{TailCoR}}}_\tau ^{jk} = {w_g}(\tau ,\xi )\widehat {{\rm{IQR}}}_\tau ^{jk}; $ | (22) |
第3步,给出非线性相关系数的估计
| $ \hat w(\tau ,\xi ,\alpha ,t) = \frac{{\widehat {{\rm{IQR}}}_\tau ^{jk}}}{{\sqrt {1 + \left| {{{\hat \rho }_{jk}}} \right|} }}. $ | (23) |
通过椭圆分布的性质,可以得到TailCoR模型中的最佳投影线是θ=π/4。参数选择上,取ξ=0.75,τ=0.95,那么对应的wg(τ, ξ)=0.410(文献[12]的附录中有给出)。由此,可以计算出4家银行之间的TailCoR,如表 2所示。
|
|
表 2 4家银行收益率之间的TailCoR Table 2 TailCoR between the yields of the four banks |
由表 2可以看出,4家银行之间的10个TailCoR都接近2,说明它们之间的相关关系很类似。在表 3和表 4中,将TailCoR进行分解,观察线性部分ρ和非线性部分w(0.95, 0.75, α)的情况。
|
|
表 3 4家银行收益率的线性相关系数 |
|
|
表 4 4家银行收益率之间的尾部非线性相关系数 Table 4 Tail nonlinear correlation coefficients between the yields of the four banks |
Kendall相关系数矩阵与皮尔逊相关系数矩阵十分接近。对于线性相关性,大型商业银行之间相关性更强,招商银行与之偏弱。对于非线性相关性,各家银行相关性比较接近,招商银行和中国银行的非线性相关性更高。
接下来,观察尾部相关性随时间的变化,可以采用分段TailCoR模型来处理。将窗宽设定为半年,样本时间分为21个时间段,分别计算各个时间段的TailCoR,以观察尾部相关性如何随时间变化。
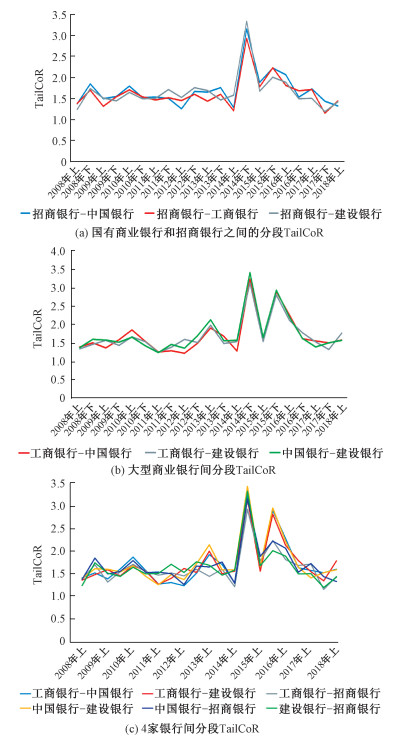
首先将4家银行的分段TailCoR显示在一个轴上,然后分别画出3家大型国有商业银行相互的TailCoR以及招商银行与大型国有商业银行之间的TailCoR,具体如图 2所示。
|
Download:
|
| 图 2 分段TailCoR Fig. 2 Segmented TailCoR | |
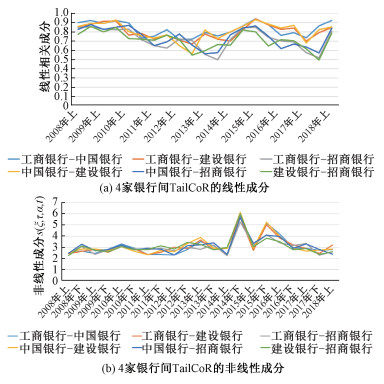
在2014年下半年牛市启动和2015年下半年牛市破灭的时候,3家大型国有商业银行的尾部相关性出现快速上升。而招商银行与其他3家大型银行之间的尾部相关性在牛市启动时快速上升,但是2015年泡沫破灭时相关性上升并不明显。下面比较4家银行TailCoR的线性和非线性成分的变化图,如图 3所示。
|
Download:
|
| 图 3 分段TailCoR分解 Fig. 3 Segmented TailCoR decomposition | |
从图 3可以看出,动态线性相关系数在整个样本区间上变化幅度较小,尾部相关性的快速上行主要由非线性部分贡献。具体来看,非线性相关系数在正常状况下为3附近,极端情况下快速上行至5~6,推动尾部相关性出现明显抬升。
由分段TailCoR可以得到以下几条结论:第一,TailCoR总体上是稳定的,在2014年下半年和2015年下半年迅速增长;第二,大型商业银行的TailCoR值波动更大,招商银行与其他3家大型国有商业银行之间的TailCoR相对稳定,在2014年下半年牛市启动的时候招商银行和大型银行的尾部相关性较强,但是在2015年股灾的时候相关性上升并不明显;第三,TailCoR中的线性部分波动小且趋势较弱,TailCoR的快速上升主要由非线性相关性上升导致。
2.3 4家银行间的动态TailCoR下面将引入外生变量,构建动态TailCoR模型。在动态TailCoR模型中,外生变量的选择较为灵活,只要外生变量能够较好地解释Ztjk的分位点,便可以得到动态TailCoR的估计。
Ramchand和Susmel[15]通过SWARCH模型,得出当美国股票市场波动剧烈时,它与其他市场间的相关性会显著上升。市场波动率会对尾部相关性产生影响,因此本文选用市场历史波动率作为外生变量。
对于上证综合指数历史波动率计算如下:
| $ {{r_t} = \ln {P_t} - \ln {P_{t - 1}},} $ | (24) |
| $ {v = \sqrt {\frac{{\sum\nolimits_{t = 1}^T {r_t^2} }}{T}} \cdot \sqrt D .} $ | (25) |
其中:Pt是上证综合指数日收盘价,D是该年的交易天数,T是该月的交易天数。
后续将使用月频数据计算动态TailCoR,所以用每月最后一天的收盘价计算对数收益率,使用式(1)和式(2)计算出投影后的随机变量Ztjk,作为被解释变量。解释变量是上证综合指数月度历史波动率vt,分别取τ1=0.95和τ2=0.05作非参数分位数回归。
在非参数分位数回归模型中,选用正态核。对于窗宽,计算公式如下
| $ h = {\left( {\frac{4}{{3n}}} \right)^{\frac{1}{5}}} \cdot \sigma , $ | (26) |
其中:σ是解释变量的标准差,n是解释变量的样本数。
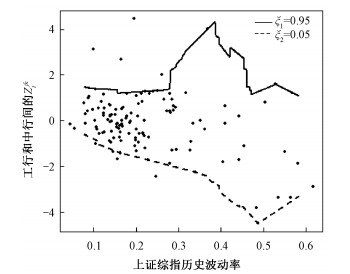
非参数分位数回归的结果比较相似,图 4中仅展示工商银行和中国银行之间的Ztjk和上证综指历史波动率的非参数分位数回归结果。
|
Download:
|
| 图 4 工行和中行间的Ztjk和上证综指历史波动率的分位数回归结果 Fig. 4 Quantile regression results of the historical volatility of Ztjk and Shanghai composite index between ICBC and BOC | |
从图 4可以看出,大多数样本的波动率小于0.4。在这一区间,两个非参数回归拟合值的差值随着波动率的上升而增加。在图像中,在波动率小于0.4的区间,τ1=0.95对应的回归曲线斜率为正,而τ2=0.05对应的回归曲线斜率为负,两者距离逐渐变大。通过非参数分位数回归,可以得到动态的IQRtjk,进而得到动态TailCoR,如图 5所示。

|
Download:
|
| 将工商银行与工商银行、中国银行、建设银行和招商银行之间的TailCoR取均值,得到工商银行TailCoR的曲线,其余类推。 图 5 4家银行之间的动态TailCoR Fig. 5 Dynamic TailCoR between the four banks | |
由图 5可以看出,在2008—2009年,4家银行的TailCoR均处于最高位置,这一阶段对应2008年股市泡沫破灭的过程。而静态TailCoR这一时间段,只有小幅度上升。在2014年下至2015年下,动态TailCoR出现了一个波峰,而静态TailCoR在2014年下、2015年下出现双峰。
下面基于DCC-GARCH模型,计算动态线性相关系数。首先,需要使用GARCH模型对边缘分布进行估计,这里使用GARCH(1, 1)模型来拟合。模型如下:
| $ {{r_{i,t}} = \mu + {\sigma _t}{\varepsilon _t},} $ | (27) |
| $ {\sigma _t^2 = \omega + \alpha {\varepsilon _{t - 1}} + \beta \sigma _{t - 1}^2.} $ | (28) |
其中εt独立同分布于标准正态。
将原数据标准化(减去均值再除以标准差)后,基于极大似然方法进行参数估计,表 5给出GARCH(1, 1)模型的估计结果,并给出了一些参数在不同置信度下的显著性检验结果。将GARCH(1, 1)中的参数估计结果代入DCC-GARCH模型中,可以得到DCC-GARCH模型的参数估计结果,具体见表 6。
|
|
表 5 4家银行股票收益率GARCH(1, 1)模型参数估计结果 Table 5 Estimation results of the GARCH(1, 1) model parameters of the four banks' stock returns |
|
|
表 6 4家银行股票收益率DCC-GARCH模型参数估计结果 Table 6 Estimation results of the DCC-GARCH model parameters of stock returns of the four banks |
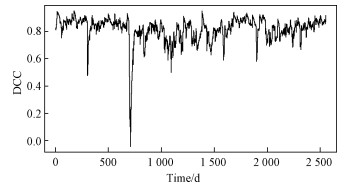
根据上述估计结果,代入DCC-GARCH模型中,可以得到动态线性相关系数,如图 6所示。
|
Download:
|
| 图 6 工商银行和中国银行间动态线性相关系数 Fig. 6 Dynamic linear correlation coefficient between ICBC and BOC | |
4家银行的动态线性相关系数走势相对平稳。到目前为止,通过引入非参数分位点回归模型,得到4家银行间的动态TailCoR,之后通过DCC-GARCH模型估计出动态线性相关系数。通过动态TailCoR和动态线性相关系数可以得到动态非线性相关部分,如图 7所示。
|
Download:
|
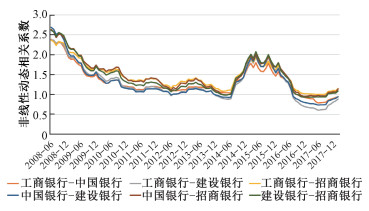
| 图 7 4家银行间动态非线性相关系数 Fig. 7 Dynamic nonlinear correlation coefficients between the four banks | |
可以看到动态非线性相关系数和动态TailCoR走势十分类似,可以认为4家银行间的TailCoR主要由非线性部分贡献。总体来看大型国有商业银行之间的TailCoR趋势性十分一致,在极端行情下尾部非线性相关系数更高,而极端情况下招商银行和其他3家大型国有商业银行的尾部相关性偏低,尾部相关性较小。
通过对动态TailCoR模型的分析,可以得到如下的结论:
第一,尾部相关性变化的原因主要是非线性相关部分,分段TailCoR模型和动态TailCoR模型都支持这一结论。在2008年和2014—2016年股票市场波动率加大时,尾部相关性上升主要是非线性部分上升导致。
第二,TailCoR在牛市启动和市场开始崩溃时会快速上升,其余时间保持稳定。
第三,中国工商银行,中国银行和中国建设银行的尾部相关性变化一致,在极端的市场条件下,尾部相关系数会显著增加。但是,招商银行与3大国有商业银行之间的尾巴相关性相对稳定。
3 结论在模型构建时,本文借鉴文献[12]提出的TailCoR模型,通过非参数分位点回归模型对模型中的分位点进行建模,得到时变的TailCoR,定义为动态TailCoR模型。
在样本服从椭圆分布的假定下,TailCoR可以进行分解,其中一部分包含皮尔逊相关系数,定义为线性相关部分,余下部分定义为非线性相关部分。本文通过DCC-GARCH模型得出动态线性相关系数,之后通过动态TailCoR和动态线性相关系数得到动态非线性相关系数。
在实证研究中,选取工商银行、中国银行、建设银行和招商银行在2008年1月至2018年6月29日的股价日收盘价收益率数据,通过原TailCoR模型、分段TailCoR模型和动态TailCoR模型,描绘4家银行股价的尾部相关性及其随时间的变化,得到以下结论:第一,尾部相关性主要是非线性部分贡献;第二,TailCoR代表的尾部相关性,在市场剧烈变动时上升,其余时间保持稳定;第三,工商银行、中国银行和建设银行的尾部相关性十分一致,并且上升十分迅速,而招商银行和3家大型国有商业银行的尾部相关性相对较低。
| [1] |
Poon S H, Rockinger M, Tawn J. Extreme value dependence in financial markets:diagnostics, models, and financial implications[J]. The Review of Financial Studies, 2003, 17(2): 581-610. |
| [2] |
Engle R F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation[J]. Econometrica, 1982, 50(4): 987-1007. Doi:10.2307/1912773 |
| [3] |
Bollerslev T. Generalized autoregressive conditional heteroskedasticity[J]. Eeri Research Paper, 1986, 31(3): 307-327. |
| [4] |
Engle R. Dynamic conditional correlation:a simple class of multivariate generalized autoregressive conditional heteroskedasticity models[J]. Journal of Business & Economic Statistics, 2002, 20(3): 339-350. |
| [5] |
Embrechts P, Lindskog F, Mcneil A. Modelling dependence with copulas and applications to risk management[J]. Handbook of Heavy Tailed Distributions in Finance, 2003, 1: 329-384. |
| [6] |
Patton A J. Modelling asymmetric exchange rate dependence[J]. International economic review, 2006, 47(2): 527-556. |
| [7] |
Rodríguez A, Moral A, Serrano L, et al. Rice straw pulp obtained by using various methods[J]. Bioresource technology, 2008, 99(8): 2881-2886. Doi:10.1016/j.biortech.2007.06.003 |
| [8] |
Straetmans S T M, Verschoor W F C, Wolff C C P. Extreme US stock market fluctuations in the wake of 9/11[J]. Journal of Applied Econometrics, 2008, 23(1): 17-42. |
| [9] |
史道济, 关静. 沪深股市风险的相关性分析[J]. 统计研究, 2003, 20(10): 45-48. |
| [10] |
韦艳华, 张世英. 金融市场的相关性分析:Copula-GARCH模型及其应用[J]. 系统工程, 2004, 22(4): 7-12. |
| [11] |
张明恒. 多金融资产风险价值的Copula计量方法研究[J]. 数量经济技术经济研究, 2004(4): 67-70. |
| [12] |
Lorenzo Ricci, David Veredas. TailCoR[R/OL]. (2015-05-13)[2019-06-27]. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2071126.
|
| [13] |
Geraci M V, Garbaravicius T, Veredas D. Short selling in extreme events[J]. Journal of Financial Stability, 2018, 39: 90-103. |
| [14] |
Lindskog F, Mcneil A, Schmock U. Kendall's tau for elliptical distributions[M]//Credit Risk. Heidelberg:Physica-Verlag HD, 2003:149-156.
|
| [15] |
Ramchand L, Susmel R. Volatility and cross correlation across major stock markets[J]. Journal of Empirical Finance, 1998, 5(4): 397-416. |
 2021, Vol. 38
2021, Vol. 38 


