2. 中国地震局地震研究所 地震大地测量重点实验室, 武汉 430071
2. Key Laboratory of Earthquake Geodesy, Institute of Seismology, China Earthquake Administration, Wuhan 430071, China
川滇地区地处青藏高原东南缘,位于西部青藏高原和东部扬子大陆地台之间的过渡地带。由于受到印度板块的推挤作用,青藏高原内物质侧向逃逸,其东缘受到华南板块的阻挡作用,东流物质向东南向—南向转移,在川滇地区形成“顺时针”旋转的运动趋势[1]。GPS观测资料进一步揭示了该区域的形变特征[2-3],在块体北部主要为东向运动,中部运动方向逐渐转为东南向—南向,南部则呈现分流趋势,即西南侧向西南方向运动,东南侧向东南方向运动。川滇地区复杂的构造变形活动,形成了川滇地区错综复杂的断层,主要发育有金沙江、怒江、澜沧江断裂带、鲜水河、安宁河、则木河、小江断裂带以及红河断裂带等具有深部构造背景的大型活动断裂带。它们组成了川滇块体的边界带[4]。
川滇地区地震震源深度主要集中在10~20 km深度处的上地壳[5],地震波速资料揭示该区域下地壳为速度较低的低速区[6],大地热流测量资料显示川滇地区平均大地热流值偏高[7],这些证据均表明川滇地区上地壳为较薄的脆性层,而中下地壳为高温的柔性层,且更容易发生流动。前人对川滇地区数值模拟的研究成果[1, 8-10]均认为青藏高原内物质被侧向挤出过程中,川滇地区的柔性下地壳流动速度较脆性上地壳快,导致脆性上地壳底部受到下地壳呈“喇叭状”的拖曳力,该拖曳作用是造成绕喜马拉雅东构造结顺时针转动的主要因素,形成川滇地区现今复杂的运动变形场。
川滇地区地表形变及深部结构的复杂性,导致区域强震频发,是中国地震最活跃、地震灾害最为严重的地区之一[4-5]。2008年汶川地震发生后,中国地震学界认为地震预报不能仅仅依靠经验预报,应该开始探索数值地震预报的方法,石耀霖等[11]提出地震数值预报的路线图,并具体提出利用二维有限单元法计算中长期时间相关的地震概率预报的方法。董培育等[12]利用该方法在青藏高原地区进行初次尝试,在计算过程中,将下地壳对上地壳的拖曳力等效为二维平面应力问题中的体力[8],然而在等效体力的估算中,主要依据经验分区及试错法的设定。尽管这种方法可以在一定程度上较好地反映出研究区域所受的下地壳的拖曳力,但也存在一定的局限性,即可能会出现不同区域之间拖曳力的不连续,同时采用试错法进行分区并寻找关键节点上的拖曳力过于依赖人为经验。
本文提出一种新的计算思路,根据川滇地区的活动地块构造,建立研究区域的二维弹性有限元模型,以GPS观测资料为约束,计算不考虑拖曳力条件下模拟的位移场与实际GPS观测的位移场之间的差值,将该差值与坐标值进行多项式拟合,该拟合关系式可以在一定程度上反映研究区域所需要的拖曳力作用,以此确定不同地点所受拖曳力大小的合理取值。该方法建立了拖曳力分布与空间坐标的数学关系,保证了拖曳力的连续性且降低了拖曳力反演试错法的主观性,为探讨川滇地区地壳运动变形的动力学机制和地震数值预报计算提供了良好基础。
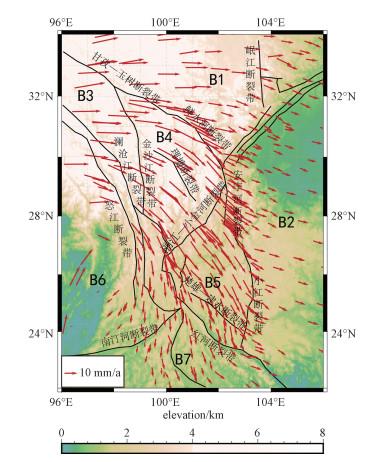
1 模型及边界条件 1.1 区域模型参考研究区域地质资料以及数值模拟的成果[13-14],同时考虑模型的边界影响,确定研究区域范围为96°~106°E, 22°~34°N,其中由图 1可知,研究区域西南角为构造环境极其复杂的阿萨姆构造结区域,该地区有限的GPS观测数据显示块体运动方向为NNE向,与其东侧(中国境内)块体运动方向(S或SW向)相反。为了减小计算结果的影响,本文模型去掉阿萨姆构造结区域,在西南角大致以国境线为边界,建立有限元数值计算模型展开研究。介质分区参照活动地块划分的结果[4, 15-17],活动块体主要包括:羌塘、巴颜喀拉、川滇、滇西、滇南及华南地块等Ⅱ级块体,其中川滇菱形块体由于受北东向丽江—小金河断裂的切割,可进一步划分为川西北和滇中两个次级块体(图 1)。
|
Download:
|
| GPS观测数据引自文献[3]。其中,B1:巴颜喀拉块体,B2:华南块体,B3:羌塘块体,B4:川西北块体,B5:滇中块体,B6:滇西块体,B7:滇南块体。 图 1 川滇地区活动地块及主要断裂带 Fig. 1 Active blocks and faults in the Sichuan-Yunnan region | |
模型中包括的断裂带主要有:甘孜—玉树断裂带、鲜水河断裂带、安宁河断裂带、则木河断裂带、小江断裂带、金沙江断裂带、红河断裂带、澜沧江断裂带、怒江断裂带、南汀河断裂带、理塘断裂带、楚雄—建水断裂带、岷江断裂带及龙门山断裂带。在计算中,将断裂带设置为具有一定宽度的软弱带,其中龙门山断裂带是由3条断层组成,故将其宽度设为10 km,其余断层的宽度设定为5 km。模型网格剖分采用三角形网格,在断裂带及边界处进行加密处理,最终得到的有限元模型共包含88 498个节点,174 280个单元。
1.2 材料参数本文计算程序采用的是FEPG自动生成的二维有限元弹性平面计算开源程序包,主要用到的材料参数为杨氏模量E和泊松比υ。根据区域层析成像研究成果获取的地壳速度结构信息[6, 18],可计算区域各个块体的杨氏模量E和泊松比υ,同时参考前人的研究成果[9, 19],将断层处理为具有一定宽度的软弱带,其杨氏模量为其所在块体的1/3左右,泊松比稍大,各块体及断裂带的具体参数选取见表 1。
|
|
表 1 介质参数表 Table 1 Material parameters |
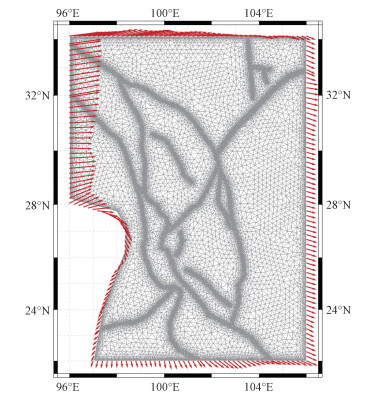
已有研究表明,GPS观测给出的现今川滇地区的地壳运动图像与晚第四纪构造变形的图像一致[20]。假设板块运动在百年尺度范围内保持恒定,在计算中选用欧亚参考框架下川滇地区1999—2015年长期GPS观测平均速度场数据作为稳定的速度场[3],将观测台站数据插值到模型边界上,作为边界约束,具体边界条件如图 2所示。
|
Download:
|
| 图 2 模型网格剖分及边界条件图 Fig. 2 The numerical model with meshs and boundary condition | |
仅加载GPS位移边界条件,不考虑柔性下地壳的拖曳作用,计算结果如图 3所示。在巴颜喀拉块体和四川盆地内观测值与模拟值吻合较好,差异较小;川滇菱形块体及滇南块体内观测值与模拟值存在明显差异:1)菱形块体北区,观测值表现为明显的东南向运动特征,而模拟值南向运动分量较小,整体表现为东向运动为主。2)菱形块体中南区,模拟值虽与观测值方向基本一致,但模拟值的运动量较观测值小。3)菱形块体南区,观测值基本为南向运动,而模拟值仍偏东南向,差异明显。4)滇南块体,主要差异表现为模拟值运动分量较小于观测值。另外值得注意的是,在滇南地区观测值有明显的东西向分流的运动趋势,在西南侧呈向西南方向运动,在东南侧呈向东南方向运动。尤其在东喜马拉雅构造结附近,表现为明显的顺时针旋转的运动形态,而计算结果并没有反映出川滇菱形块体顺时针旋转的趋势。综合观测结果与初步计算结果表明:在构造复杂的川滇地区仅考虑脆性上地壳弹性变形是不够的,因此,需要在弹性模型中考虑柔性下地壳流动对脆性上地壳产生的附加拖曳作用[1, 8]。前人在川滇地区数值模拟过程中采用不同的方法考虑了拖曳力的影响,朱守彪和石耀霖[8]采用遗传算法反演,利用逐渐逼近的方法,进行大量迭代计算搜索得到最佳匹配模型;王辉等[9]利用在滇南地区边界上加大其速度场,模拟区域形变能够与实际吻合,上述方法取得了一定成果但缺乏数学物理规律且需要大量试错并不断重复计算。

|
Download:
|
| 图 3 仅加载GPS边界条件的计算结果 Fig. 3 The results only with GPS boundary conditions | |
本文提出一种新的思路来计算川滇地区下地壳流对上地壳的拖曳作用。将未考虑拖曳力的模拟结果与实际GPS观测资料结果之间的位移场差值(如图 3(b)所示)记为ΔUx和ΔUy,其与坐标x(东西向),y(南北向)之间的关系在一定程度上可以反映研究区域需要施加的拖曳力与坐标的关系。因此尝试将ΔUx,ΔUy与x,y进行多项式拟合并将该拟合关系式乘以适当的比例因子来反映研究区域所需要的适当大小的拖曳力。通过试错法,找到模型中各个点位上的拖曳力,令最终计算结果可与实测值最佳吻合,具体计算如下:
本文共选用远离边界区域的357个均匀节点的值(ΔUx,ΔUy,x,y),进行多项式拟合,经过尝试,认为3次拟合精度即可满足计算需求。x方向上任意点位的拟合公式如式(1)所示,多点位的拟合公式(矩阵形式)如式(2)所示,y方向上的拟合公式同x方向拟合公式类似,如式(3)所示,其中式(2)和式(3)中的n代表点位号(n=1, 2,…,357)。
| $ \begin{array}{l} \Delta {u_x} = {P_{00}^x} + {P_{10}^x}x + {P_{01}^x}y + {P_{20}^x}{x^2} + {P_{11}^x}xy + \\ \ \ {P_{02}^x}{y^2} + {P_{30}^x}{x^3} + {P_{21}^x}{x^2}y + {P_{12}^x}x{y^2} + {P_{03}^x}{y^3}, \end{array} $ | (1) |
| $ \begin{array}{l} {\left[\begin{array}{llllllllll} 1 & x_{1} & y_{1} & x_{1}^{2} & x_{1} y_{1} & y_{1}^{2} & x_{1}^{3} & x_{1}^{2} y_{1} & x_{1} y_{1}^{2} & y_{1}^{3} \\ 1 & x_{2} & y_{2} & x_{2}^{2} & x_{2} y_{2} & y_{2}^{2} & x_{2}^{3} & x_{2}^{2} y_{2} & x_{2} y_{2}^{2} & y_{2}^{3} \\ &&&&& \cdots &&&&\\ 1 & x_{n} & y_{n} & x_{n}^{2} & x_{n} y_{n} & y_{n}^{2} & x_{n}^{3} & x_{n}^{2} y_{n} & x_{n} y_{n}^{2} & y_{n}^{3} \end{array}\right]} \\ \ \ \ \ \ \ \ \ \ {\left[\begin{array}{l} P_{00}^{x} \\ P_{10}^{x} \\ \cdots \\ P_{03}^{x} \end{array}\right]} = {\left[\begin{array}{c} \Delta u_{x 1} \\ \Delta u_{x 2} \\ \cdots \\ \Delta u_{x n} \end{array}\right], } & \end{array} $ | (2) |
| $\left[\begin{array}{cccccccccc} 1 & x_{1} & y_{1} & x_{1}^{2} & x_{1} y_{1} & y_{1}^{2} & x_{1}^{3} & x_{1}^{2} y_{1} & x_{1} y_{1}^{2} & y_{1}^{3} \\ 1 & x_{2} & y_{2} & x_{2}^{2} & x_{2} y_{2} & y_{2}^{2} & x_{2}^{3} & x_{2}^{2} y_{2} & x_{2} y_{2}^{2} & y_{2}^{3} \\ & & & & & \ldots & & & & \\ 1 & x_{n} & y_{n} & x_{n}^{2} & x_{n} y_{n} & y_{n}^{2} & x_{n}^{3} & x_{n}^{2} y_{n} & x_{n} y_{n}^{2} & y_{n}^{3} \end{array}\right]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left[\begin{array}{l} P_{00}^{y} \\ P_{10}^{y} \\ \ldots \\ P_{03}^{y} \end{array}\right]=\left[\begin{array}{c} \Delta u_{y 1} \\ \Delta u_{y 2} \\ \cdots \\ \Delta u_{y n} \end{array}\right]. $ | (3) |
经计算得到的x方向和y方向的拟合系数见表 2。
|
|
表 2 多项式拟合系数 Table 2 Polynomial fitting coefficients |
位移差值与坐标的关系拟合公式,可以在一定程度上反映出计算中忽略掉的下地壳对上地壳的拖曳力作用,考虑利用该拟合关系乘以一定的比例因子来表示模型中拖曳力Fx、Fy与x、y的关系。经过试错,最终得到比例因子东西向为5.0e+5,南北向为1.0e+6,以此得到不同点位上的拖曳力,如图 4所示。该方法可以得到研究区域内连续渐变的拖曳力分布,在物理上更加合理,方法上更加客观简洁。由图 4可以看出,拖曳力的分布形态及大小与位移差相似,主要集中在川滇菱形块体中北区域,且以南向为主;菱形块体的南部,拖曳力则呈现出东西向分流的形式,且拖曳力值较小。最后利用前人的方法[8, 11],如式(4)所示,在二维弹性平衡方程中将水平剪应力分量垂向偏导数
| $ \left\{ \begin{array}{l} \frac{{\partial {\sigma _{xx}}}}{{\partial x}} + \frac{{\partial {\sigma _{xy}}}}{{\partial y}} + \left( {\frac{{\partial {\sigma _{xz}}}}{{\partial z}} + {f_x}} \right) = 0\\ \frac{{\partial {\sigma _{xy}}}}{{\partial x}} + \frac{{\partial {\sigma _{yy}}}}{{\partial y}} + \left( {\frac{{\partial {\sigma _{yz}}}}{{\partial z}} + {f_y}} \right) = 0 \end{array} \right.. $ | (4) |

|
Download:
|
| 图 4 加载至模型中的拖曳力 Fig. 4 Drag force in this model | |
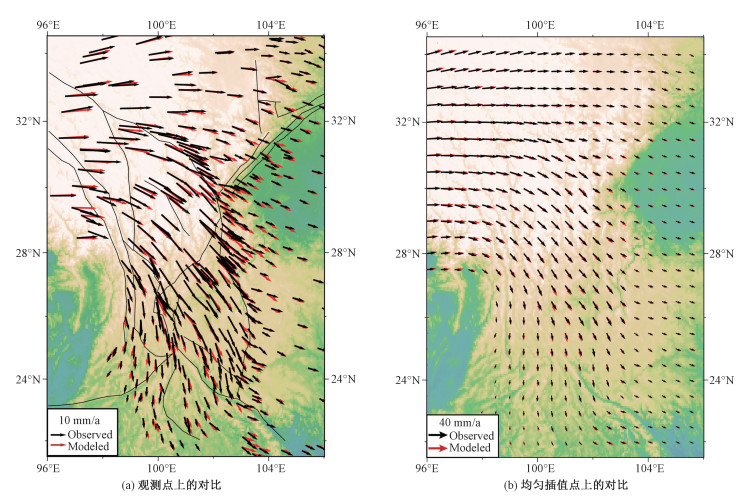
考虑脆性上地壳变形和柔性下地壳拖曳共同作用的计算结果与实际GPS观测结果的比较如图 5所示,模拟得到的GPS速度值与观测值之间可比性较高,先前速度场差异较大的川滇菱形块体内部在加载拖曳力后得到了很大改善,仅在个别地区存在误差(东喜马拉雅构造结附近的观测点不列入考虑)。根据式(5)计算二者之间的均方根误差,计算结果如表 3所示,加载拖曳力后的模拟值均方根误差明显小于未加载拖曳力的情况。
| $ {\rm{RMSE}} = \sqrt {\frac{{\mathit{\Delta} _1^2 + \mathit{\Delta} _2^2 + \ldots + \mathit{\Delta} _n^2}}{n}} = \sqrt {\frac{{\sum {\mathit{\Delta} _i^2} }}{n}} , $ | (5) |
|
Download:
|
| 图 5 施加拖曳力的模型计算结果与观测值对比图 Fig. 5 Comparison between the observed and the simulated value with drag force in the model | |
|
|
表 3 计算结果与观测值均方根误差对比 Table 3 Comparison of root mean square error between the calculated and observed values |
式中:n是所有加载拖曳力的节点的个数,Δi是每个节点的计算值和观测值之差,RMES是均方根误差。
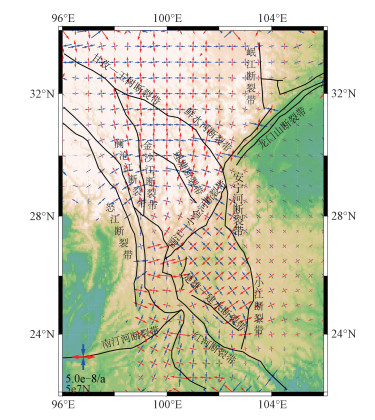
在此基础上计算得到川滇地区的水平主应变率场如图 6所示,该计算结果与前人根据GPS观测速度场数据利用最小二乘配置应变率计算方法计算得到的研究区域主应变场,在大小及方向上均具有较好的一致性[21-22]。进一步分析研究区域应变率,大致估计研究区域断层错动方向,由图 6可以看出在龙门山断裂带上挤压应变明显高于拉伸应变,处于逆冲型环境。而在川滇菱形块体边界带上大部分区域表现为拉伸和挤压应变大小相当,以走滑型为主。沿着甘孜—玉树,鲜水河断裂带向南延伸,水平主压应变方向由近EW向逐渐变为NWW向,以左旋走滑为主;南段安宁河—则木河段主压应变方向持续变化为NW向,在小江断裂带上变化为NNW向,在其南端,接近NS向,均以左旋走滑为主。金沙江断裂北段受到近EW向的挤压和近NS向的拉张,其南段主压应变方向转为NNW向,整体表现为右旋走滑;丽江—小金河断裂主压应变方向为NW向,张应变方向为NE向,主要表现为逆冲左旋走滑;红河断裂北段主压应变方向为NW向,随着断裂带向南延伸,主压应变转为近水平向,以右旋走滑为主;澜沧江断裂带北段主压应变方向为近EW向,南段转为NE向,南汀河断裂主要压应变方向为NE向,成左旋走滑。模拟得到的主要断层的滑动性质与实际断层滑动性质均一致(具体见表 4),一定程度上验证了计算的正确性。
|
Download:
|
| 蓝色箭头为压缩分量, 红色箭头为拉张分量。 图 6 模拟计算的应变率场 Fig. 6 Simulated strain rate field | |
|
|
表 4 川滇地区主要活动断裂性质 Table 4 The characteristics of the main faults in the Sichuan-Yunnan region |
本文以GPS观测数据为约束条件,依据川滇地区构造活动特征建立二维有限元弹性平面模型,考虑柔性下地壳差异性快速流动对脆性上地壳的拖曳作用,并以等效体力的形式加载至模型中。拖曳力的反演计算通过拟合弹性模型中计算结果与实测值之间的位移差和坐标点之间的关系,并通过试错法计算得到,模拟的结果可以较好地反映川滇地区的实际运动变形和受力情况。本文计算结果表明,研究区域拖曳力可能主要集中在川滇菱形块体的中北部地区,且主要为南向;在菱形块体的南部则可能存在东南向的拖曳力;在其西侧即滇西地区可能存在西南向的拖曳力。与前人[8, 12]反演的川滇地区下地壳拖曳力方向、大小等结果基本保持一致。但本研究方法是基于位移残差与坐标的数学关系拟合得到,据此数学关系,仅需调节合理的比例因子,提高了人为试错分区计算的效率。同时该方法可以得到研究区域内连续渐变的拖曳力分布,相比于人为试错寻找关键节点上拖曳力的做法,该方法在物理上更加合理,方法上更加客观,可以为川滇地区的长期地表形变动力学机制研究提供一种更简洁的新思路。
本文是基于二维弹性模型基础上的一种简洁推演计算,仅是对真实地质模型的一种近似最优解。在相关问题的深入研究中,考虑真实的柔性下地壳与脆性上地壳之间的拖曳关系,仍需要通过建立更加接近实际地壳分层结构的三维模型,采用更加精细的介质和断层参数,才能够得到更加精确的结果。
| [1] |
曹建玲, 石耀霖, 张怀, 等. 青藏高原GPS位移绕喜马拉雅东构造结顺时针旋转成因的数值模拟[J]. 科学通报, 2009, 54(2): 224-234. |
| [2] |
Wang Q, Zhang P Z, Freymueller J T, et al. Present-day crustal deformation in China constrained by global positioning system measurements[J]. Science, 2001, 294(5542): 574-577. Doi:10.1126/science.1063647 |
| [3] |
Zheng G, Wang H, Wright T J, et al. Crustal deformation in the India-Eurasia collision zone from 25 years of GPS measurements:crustal deformation in Asia from GPS[J]. Journal of Geophysical Research Solid Earth, 2017, 122(11): 9290-9312. Doi:10.1002/2017JB014465 |
| [4] |
张培震, 邓起东, 张国民, 等. 中国大陆的强震活动与活动地块[J]. 中国科学D辑:地球科学, 2003, 33(S1): 12-20. |
| [5] |
马宏生, 张国民, 周龙泉, 等. 川滇地区中小震重新定位与速度结构的联合反演研究[J]. 地震, 2008, 28(2): 29-38. |
| [6] |
王椿镛, 韩渭宾, 吴建平, 等. 松潘-甘孜造山带地壳速度结构[J]. 地震学报, 2003, 25(3): 229-241, 342. Doi:10.3321/j.issn:0253-3782.2003.03.001 |
| [7] |
姜光政, 高堋, 饶松, 等. 中国大陆地区大地热流数据汇编(第四版)[J]. 地球物理学报, 2016, 59(8): 2892-2910. |
| [8] |
朱守彪, 石耀霖. 用遗传有限单元法反演川滇下地壳流动对上地壳的拖曳作用[J]. 地球物理学报, 2004, 47(2): 232-239. Doi:10.3321/j.issn:0001-5733.2004.02.009 |
| [9] |
王辉, 曹建玲, 张怀, 等. 川滇地区下地壳流动对上地壳运动变形影响的数值模拟[J]. 地震学报, 2007, 29(6): 581-591, 671. |
| [10] |
庞亚瑾, 程惠红, 张怀, 等. 青藏高原东缘岩石圈结构对现今地表垂向运动影响的数值分析[J]. 地球物理学报, 2019, 62(4): 1256-1267. |
| [11] |
石耀霖, 孙云强, 罗纲, 等. 关于我国地震数值预报路线图的设想:汶川地震十周年反思[J]. 科学通报, 2018, 63(19): 1865-1881. |
| [12] |
董培育, 胡才博, 石耀霖. 青藏高原及周边区域地表长期变形数值模拟[J]. 地震地质, 2016, 38(2): 410-422. |
| [13] |
Shen Z K, Lv J N, Wang M, et al. Contemporary crustal deformation around the southeast borderland of the Tibetan Plateau[J]. Journal of Geophysical Research Solid Earth, 2005, 110(B11): 409-425. |
| [14] |
He J K, Lu S J, Wang W M. Three-dimensional mechanical modeling of the GPS velocity field around the northeastern Tibetan plateau and surrounding regions[J]. Tectonophysics, 2013, 584(SI): 257-266. |
| [15] |
徐锡伟, 闻泽学, 郑荣章, 等. 川滇地区活动块体最新构造变动样式及其动力来源[J]. 中国科学D辑:地球科学, 2003, 33(S1): 151-162. |
| [16] |
乔学军, 王琪, 杜瑞林. 川滇地区活动地块现今地壳形变特征[J]. 地球物理学报, 2004, 47(5): 806-812. |
| [17] |
邓起东, 张培震, 冉永康, 等. 中国活动构造与地震活动[J]. 地学前缘, 2003, 10(S1): 66-73. |
| [18] |
韦伟, 孙若昧, 石耀霖. 青藏高原东南缘地震层析成像及汶川地震成因探讨[J]. 中国科学D辑:地球科学, 2010, 40(7): 831-839. |
| [19] |
陈化然, 陈连旺, 马宏生, 等. 川滇地区应力场演化与强震间相互作用的三维有限元模拟[J]. 地震学报, 2004, 26(6): 567-575. |
| [20] |
Royden L H, Clark B B, Van Der Hilst R D. The geological evolution of the Tibetan Plateau[J]. Science, 2008, 321(5892): 1054-1058. |
| [21] |
武艳强, 江在森, 杨国华, 等. 汶川地震前GPS资料反映的应变率场演化特征[J]. 大地测量与地球动力学, 2011, 31(5): 20-25, 29. |
| [22] |
魏文薪, 江在森, 刘晓霞, 等. 川滇地区应变率场分布及其变化特征研究[J]. 地震, 2015, 35(4): 11-20. |
| [23] |
张培震. 青藏高原东缘川西地区的现今构造变形、应变分配与深部动力过程[J]. 中国科学D辑:地球科学, 2008, 38(9): 1041-1056. |
| [24] |
唐荣昌, 韩渭宾. 四川活动断裂与地震[M]. 北京: 地震出版社, 1993.
|
 2021, Vol. 38
2021, Vol. 38 


