我国结核病发病数位居全球的第3位,属于全球结核病高负担国家[1]。因此,肺结核发病趋势、发病人数和发病率等问题在我国受到医务工作者、医疗卫生管理人员和医学研究人员的广泛关注。秘玉清等[2]使用自回归移动平均(ARIMA)模型对山东省2009—2017年肺结核发病率进行了预测研究。付之鸥等[3]使用ARIMA、SVR、BPANN、ARIMA-SVR、ARIMA-BP模型对江苏省2009—2018年肺结核发病趋势进行了预测研究。林淑芳等[4]使用ARIMA模型对福建省2010—2019年肺结核发病率进行了预测研究。
《疾病监测》2022年第5期刊登了一篇题为《基于自回归移动平均模型的浙江省肺结核发病趋势预测》的文献[5],该文作者使用浙江省2011—2021年肺结核月度发病率时序数据,构建ARIMA模型对浙江省肺结核发病率进行预测。本文第一作者楼润平(以下简称“笔者”)在著作[6]中提出了三体模型和三体预测法,该预测模型和预测方法泛化能力强,简洁实用,且适用于多个场景。
鉴于此,本文拟使用文献[6]提出的三体模型和三体预测法,使用与文献[5]同样的数据集(即浙江省2011—2021年肺结核月度发病率数据)进行预测研究,并与文献[5]所述ARIMA模型的预测性能进行比较。希望该研究过程及其结果能为广大读者提供有益的认识和启示,能为医学界的研究人员、管理人员、医务工作者开展相关预测研究提供有益的实践参考,能为学术界提供文献借鉴和文献积累。
1 资料与方法 1.1 资料来源2011年1月—2021年12月浙江省肺结核发病率原始数据来源于中国疾病预防控制信息系统和《浙江统计年鉴》。为便于比较,本文使用的训练集和测试集与文献[5]相同,即本文以2011年1月—2020年12月浙江省肺结核发病率时序数据作为训练集,以2021年1—8月浙江省肺结核发病率时序数据作为测试集,同时报告了2021年1—12月浙江省肺结核发病率的平均相对预测误差(mean relative prediction error, MRPE)。
1.2 研究方法笔者提出了三体模型和三体预测法[6],该预测模型和预测方法简洁实用,泛化能力强。该书提供了大约30个实例及原始数据,读者可以复制出跟书中完全一样的预测模型、预测结果和可视化图形。该预测模型和预测方法适用于日度、月度、季度和年度等级别的时间序列[6]。
1.2.1 时间序列的特征及分类对于时间序列的特征,不同学者从不同视角出发,形成各自的归类。伍德里奇[7]认为,时间序列具有趋势、季节、冲击、长期和累积等特征。韩伯棠[8]认为,时间序列具有趋势、季节、周期和不规则四个特征。笔者将时间序列的特征简要归结为趋势、波动和惯性[6]。
时间序列的诸多特征互相叠加、组合,形成了类型多样的时间序列。基于对时间序列特征的简化归类及独特认识,笔者将纷繁多样的时间序列归结为三类,并以形象名字“青云直上”“一江春水向东流”“形影不离”命名[6]。
1.2.2 三体模型和三体预测法文献[6]中提出的“三体模型”如下所示:
| $ y_t=\beta_0+\beta_1 t+\sum\nolimits_{\mathrm{i}=1}^{\mathrm{m}} \theta_i x_i+\sum\nolimits_{\mathrm{j}=1}^3 \delta_j y_{\mathrm{t}-\mathrm{j}}+\varepsilon $ | (公式Ⅰ) |
在公式Ⅰ中,β0为常数项,ε为误差项。t为单位时间变量,用于描述时间序列的趋势。t的初值设为1,按步长1依次递增。xi为描述波动特征的变量,为0~1虚拟变量。yt为因变量,当j=1、2、3时,yt-j分别为滞后一阶、二阶、三阶因变量。yt-j主要用于衡量时间序列的惯性特征。文献[6]中提出的三体预测法如图 1所示:
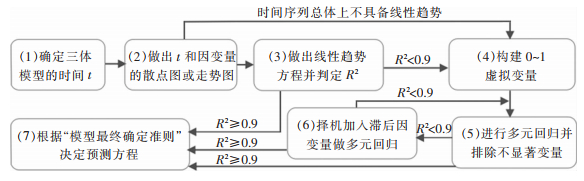 |
| 图 1 笔者提出的三体预测法框架 Figure 1 Framework of trinity forecasting method |
文献[6]提出了确定三体模型的三个准则,分别为R2平方准则、简洁准则、相对预测误差(relative prediction error, RPE)准则。文献[6]使用三体模型和三体预测法对大约30个实例进行了演示,这些实例涉及了手机出货量、猪肉消费量、冰箱需求量、机场客运量、集装箱吞吐量、电子废弃物回收量、垃圾清运量、微信用户数量、中国国内生产总值(GDP)、城镇家庭人均收入、农村家庭人均收入等场景。上述30个实例涉及了时间序列日度、月度、季度、年度级别时序。
1.3 预测模型的预测性能应用预测误差来衡量预测模型的预测表现(即预测性能)。预测值偏离真实值(或实际值)的幅度,称为预测误差。衡量预测误差的公式有多个,本文在此使用RPE和MRPE。
(1) RPE:
| $ \begin{aligned} & R P E_i=\frac{\mid { 真实值 }- { 预测值 } \mid}{{真实值}} \times 100 \%=\frac{\left|R_i-F_i\right|}{R_i} \times 100 \% \end{aligned} $ | (公式Ⅱ) |
(2) MRPE:
| $ M R P E=\frac{\sum\nolimits_i^n R P E_i}{n} $ | (公式Ⅲ) |
在公式Ⅱ、Ⅲ中,Ri表示第i个真实值,Fi表示第i个预测值,i为标号(i=1, 2, …n),n为测试集的样本数量。
1.4 统计学分析应用Excel软件对时间序列月度数据进行汇总整理,通过Stata软件对时序数据进行建模及回归分析,按照三体预测法框架获得回归结果和预测模型。
2 结果 2.1 浙江省肺结核发病率走势图和趋势线根据三体预测法的操作步骤,先做出2011年1月—2021年12月浙江省肺结核发病率走势图,见图 2。通过鸟瞰视图,可以直观看出:该时间序列具有典型的趋势特征;许多数据点远离趋势线,波动幅度较大,表明该时间序列具有典型的波动特征。
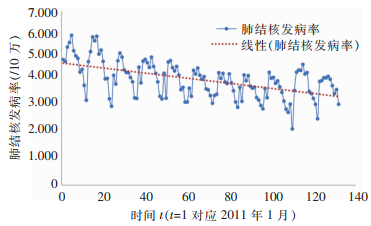 |
| 图 2 2011年1月—2021年12月浙江省肺结核发病率走势及趋势图 Figure 2 PTB incidence trends in Zhejiang Province from January 2011 to December 2021 |
图 2所示的时间序列具有典型的波动特征,时间序列类别属于“形影不离”,时间序列在三体模型中设置波动变量和惯性变量,即可做出具有优秀预测表现的预测模型。
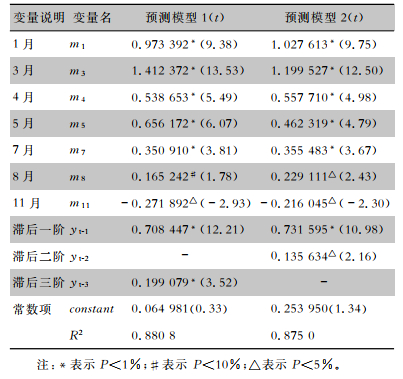
2.3 预测模型的建立依据图 1所示的三体预测法框架,以2011年1月—2020年12月浙江省肺结核发病率时序数据作为训练集,获得两个符合要求的预测模型,见表 1。预测模型1、预测模型2的R2分别为0.880 8、0.875 0,表明此两个预测模型均能解释浙江省肺结核发病率大约88%的变化。
| 表 1 浙江省肺结核发病率月度数据预测模型 Table 1 Forecasting model based on monthly PTB incidence data in Zhejiang Province |
|
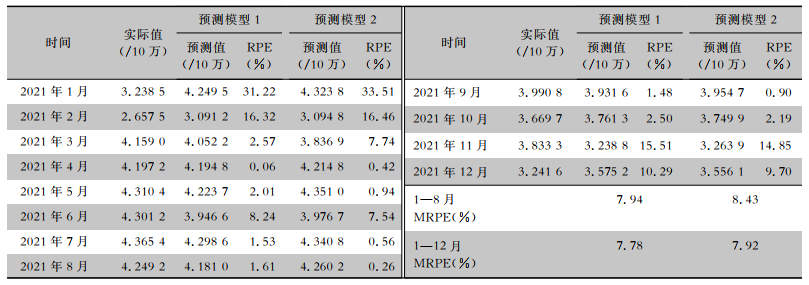
使用表 1所示的预测模型1和预测模型2,计算2021年1—12月每个月浙江省肺结核发病率预测值;根据公式Ⅱ,分别获得预测模型1和预测模型2每个月的RPE值;根据公式Ⅲ,分别计算2021年1—8月和1—12月预测模型1和预测模型2的MRPE值,结果显示2021年1—8月预测模型1和预测模型2的MRPE分别为7.94%、8.43%,其预测误差在可接受范围内,模型预测表现优秀。2021年1—12月预测模型1和预测模型2的MRPE分别为7.78%、7.92%,模型预测表现优秀。见表 2。
| 表 2 2021年1—12月浙江省肺结核发病率实际值、预测值和预测误差 Table 2 Actual value, predicting value and predicting error of PTB incidence in Zhejiang Province from January to December 2021 |
|
为进一步评估上述两个预测模型对2022年浙江省肺结核发病率的预测表现,收集了2022年1—12月浙江省肺结核发病人数,然后使用公式“发病率=新增病例数/同年份常住人口数”计算出对应月份的发病率。见表 3。
| 表 3 2011年1月—2022年12月浙江省肺结核发病率(/10万) Table 3 PTB incidence in Zhejiang Province from January 2011 to December 2022 (/100 000) |

|
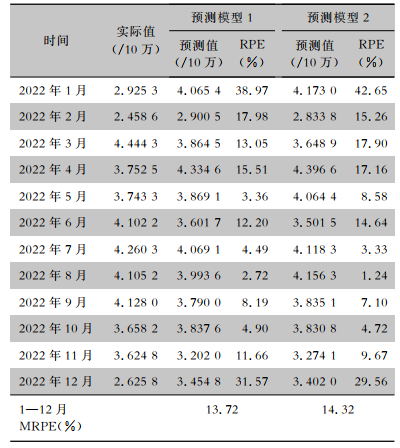
对预测模型而言,其对测试集的MRPE在(0, 10%),则定义为预测表现优秀;MRPE在(10%, 15%),则定义为预测表现良好。使用表 1的预测模型1和预测模型2,分别对2022年1—12月浙江省肺结核发病率进行预测,MRPE分别为13.72%、14.32%,两者均处于(10%, 15%),说明预测表现良好。见表 4。
| 表 4 2022年1—12月浙江省肺结核发病率实际值、预测值和预测误差 Table 4 Actual value, predicting value and predicting error of PTB incidence in Zhejiang Province from January to December 2022 |
|
为便于直观比较,以2021年1—12月为横坐标,2021年1—12月浙江省肺结核发病率实际值、预测模型1和2的预测值为纵坐标,做出了2021年1—12月浙江省肺结核发病率实际值和预测值走势图,结果显示预测值的曲线走势非常贴近实际值的曲线走势,说明预测值与真实值之间的误差相对较小。见图 3。
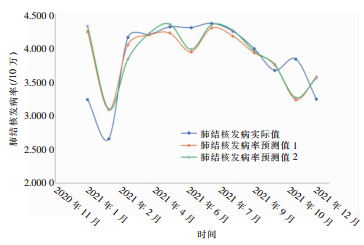 |
| 图 3 2021年1—12月浙江省肺结核发病率实际值和预测值走势曲线图 Figure 3 Curves of actual PTB incidence and trends of predicting PTB incidence in Zhejiang Province from January to December 2021 |
以2011年1月—2020年12月浙江省肺结核发病率月度时序数据作为训练集,2021年1—8月浙江省肺结核发病率月度时序数据作为测试集,使用ARIMA模型计算出MRPE为8.87%[5]。本研究通过预测模型1和预测模型2获得的MRPE分别为7.94%、8.43%,预测误差令人满意,模型预测表现优秀。三体模型和ARIMA模型之间的MRPE非常接近,均处于区间(7.9%~8.9%),均属于表现优秀的预测模型。
3 讨论评价预测模型之间的优劣,可以从三个方面进行考察:(1)预测模型的预测误差。对于预测模型而言,其预测误差越小,预测表现越好,此种评价指标显而易见。(2)预测模型的泛化能力。对于预测模型而言,其泛化能力(即一般化能力)越强,则适用场景越多,越具备广泛应用价值。(3)预测模型的简洁实用。基于成本收益视角,在同等预测表现的情况下,简洁实用的预测模型比复杂的好。
本研究基于三体模型和三体预测法,使用与文献[5]同样的训练集,即以2011年1月—2020年12月浙江省肺结核发病率月度时序数据作为训练集,获得两个有价值的预测模型1和预测模型2。本研究使用与文献[5]同样的测试集,即以2021年1—8月浙江省肺结核发病率月度时序数据作为测试集,经过对比分析,获得预测模型1和预测模型2的MRPE分别仅为7.94%、8.43%,预测性能优秀。文献[6]指出,最终预测模型的确定准则之一,是R2要达到0.9,此准则属于高标准要求。在某些案例和场景中,R2接近0.9,也是可以接受的。因此,上述两个预测模型是令人满意的。
对2011年1月—2021年12月浙江省肺结核发病率月度时序数据开展的预测研究表明,三体模型和三体预测法泛化能力强健,应用场景广泛。笔者期待未来有研究人员使用三体预测法就其他省份的肺结核发病率时序数据开展预测研究,以便进一步检验三体模型和三体预测法的泛化能力。
本研究基于三体模型和三体预测法对浙江省肺结核发病率月度时序数据开展的预测研究过程及其结果表明,三体模型和三体预测法简洁实用:做出时序数据走势图,判断时间序列的特征及类别,依据三体预测法做出预测模型,评估预测模型的预测表现。笔者认为,在能够解决实践问题并且实效相同的情况下,从成本收益视角而言,简洁实用的模型比复杂的更值得推广。
对于2011年1月—2022年12月浙江省肺结核发病率月度时间序列,1月份数据波动较大,而本文的预测模型和预测方法未能充分捕获,导致预测误差较大,从而影响了预测模型的综合表现。比如,以2022年全年的月度时间序列作为测试集,则预测模型的预测表现只达到了良好,而未能达到优秀。这是本文不足之处,未来尚需进一步改进。
利益冲突:所有作者均声明不存在利益冲突。
| [1] |
王威, 叶一农, 吴智龙, 等. 2010—2020年广东省佛山市肺结核发病趋势及流行特征分析[J]. 疾病监测, 2021, 36(10): 1039-1043. Wang W, Ye YN, Wu ZL, et al. Incidence trend and epidemio-logical characteristics of pulmonary tuberculosis in Foshan, 2010-2020[J]. Disease Surveillance, 2021, 36(10): 1039-1043. |
| [2] |
秘玉清, 张继萍, 殷延玲, 等. 基于ARIMA模型的山东省肺结核发病趋势预测[J]. 中国卫生统计, 2018, 35(6): 879-881. Mi YQ, Zhang JP, Yin YL, et al. Prediction of tuberculosis incidence trend in Shandong province based on ARIMA model[J]. Chinese Journal of Health Statistics, 2018, 35(6): 879-881. |
| [3] |
付之鸥, 周扬, 陈诚, 等. 时间序列分析与机器学习方法在预测肺结核发病趋势中的应用[J]. 中国卫生统计, 2020, 37(2): 190-195. Fu ZO, Zhou Y, Chen C, et al. Application of time series analysis and machine learning methods in predicting the incidence of tuberculosis[J]. Chinese Journal of Health Statistics, 2020, 37(2): 190-195. |
| [4] |
林淑芳, 周银发, 张山鹰, 等. 2010—2019年福建省肺结核流行特征及发病预测模型应用[J]. 中华疾病控制杂志, 2021, 25(7): 768-774. Lin SF, Zhou YF, Zhang SY, et al. Analysis of tuberculosis epidemiological characteristics and application of incidence prediction model in Fujian Province from 2010 to 2019[J]. Chinese Journal of Disease Control & Prevention, 2021, 25(7): 768-774. |
| [5] |
茅蓉, 王远航, 葛锐. 基于自回归移动平均模型的浙江省肺结核发病趋势预测[J]. 疾病监测, 2022, 37(5): 652-656. Mao R, Wang YH, Ge R. Prediction of incidence of pulmonary tuberculosis in Zhejiang based on autoregressive integrated moving average[J]. Disease Surveillance, 2022, 37(5): 652-656. |
| [6] |
楼润平. 经济管理预测实用方法: 三体模型和三体预测法[M]. 北京: 经济科学出版社, 2023. Lou RP. Practical methods for economic and management forecasting: trinity model and trinity forecasting method[M]. Beijing: Economic Science Press, 2023. |
| [7] |
杰弗里·M. 伍德里奇. 计量经济学导论: 现代观点[M]. 6版. 北京: 中国人民大学出版社, 2018. Wooldridge JM. Introductory econometrics introductory eco-nometrics: a modern approach[M]. 6th ed. Beijing: China Renmin University Press, 2018. |
| [8] |
韩伯棠. 管理运筹学[M]. 5版. 北京: 高等教育出版社, 2020. Han BT. Management operations research[M]. 5th ed. Beijing: Higher Education Press, 2020. |



