2. 中国科学院上海应用物理研究所,上海 201800
2. Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Shanghai 201800 China
碳离子治疗是一种新型离子束疗法,近年来受到人们的极大关注[1]。相较于传统的放射治疗方法(X射线、γ射线和电子束),其最大优势得益于碳离子束具有的布拉格(Bragg)峰[2-3],能够根据肿瘤所处位置,通过调节碳离子束入射能量使其Bragg峰扩展覆盖到所需要的体积,让能量精准沉积在靶区体积内,从而显著地减少对肿瘤附近正常器官和组织的辐射损伤。另外,碳离子具有高传能线密度(Linear energy transfer,LET)及相对生物效应,其在剂量局域性和生物学效应方面优于质子治疗[4-5]。
由于碳离子能量损失及沉积特性,在治疗过程中,人体非均匀组织对碳离子Bragg峰的位置分布造成很大影响。因此对于碳离子治疗,精准确定特定能量碳离子在组织中的深度剂量分布和Bragg峰位置,对后续计划制定及治疗效果具有重要的意义。随着计算机技术的迅猛发展,蒙特卡罗方法在高能物理、医学等领域得到广泛应用[6-8]。本研究基于构建在蒙特卡罗方法之上的SRIM软件,其具有操作方便、简单易学等特点,并能够在10 eV~2 GeV/u的能量范围内模拟入射离子在材料中的输运情况[9]。本工作利用SRIM-2013软件对100~300 MeV/u的碳离子束在不同材料中的能量沉积特性进行研究,同时探究了介质材料及厚度、碳离子入射能量等因素对碳离子束Bragg峰位置分布的影响,并探索利用人体各组织CT值数据,精确计算碳离子束所需入射能量,使得高剂量峰位精准分布在肿瘤部位,以期为碳离子束精准和安全治疗肿瘤提供数据支撑。
1 材料与方法 1.1 Bethe公式带电粒子在穿过介质时会与靶原子发生相互作用而损失能量,这一过程中主要包括与靶原子核的弹性碰撞以及与核外电子非弹性碰撞,也就是通常所说的核阻止及电子阻止[10]。一般碳离子治疗采用的离子能量范围为几十至几百MeV/u,此时碳离子在人体组织中能量沉积的主要方式是电子阻止。在某些假设下,重离子在介质中的电子阻止本领可以由相对论Bethe公式给出,相应的表达式如式1)[11]:
| $ {{ - }}\frac{{dE}}{{dx}} = \frac{{4{\text{π }}n{z^2}}}{{{m_e}{c^2}{\beta ^2}}}{\left( {\frac{{{e^{\text{2}}}}}{{{{4\pi }}{\varepsilon _0}}}} \right)^2}\left( {\ln \left( {\frac{{2{m_e}{c^2}{\beta ^2}}}{{I(1 - {\beta ^2})}}} \right) - {\beta ^2}} \right) $ | (1) |
式中E表示能量,x为粒子穿行距离,n是材料的电子密度,z为电荷数,c表示的是光速,v为粒子速度,e为电子电荷,ε0是真空介电常数,me是电子静止质量,I为平均激发能,
对于低能带电粒子,β
| $ {{ - }}\frac{{dE}}{{dx}} = \frac{{4{\text{π }}n{z^2}}}{{{m_e}}}{\left( {\frac{{{e^2}}}{{{{4\pi }}{\varepsilon _0}}}} \right)^2}\left( {\frac{1}{{{v^2}}}} \right)\left( {\ln \frac{{2{m_e}{v^2}}}{I}} \right) $ | (2) |
从Bethe公式可以看出带电粒子的能量损失率反比于粒子速度的平方,这就解释了为何能量损失率的尖峰即Bragg峰会出现在带电粒子刚好完全停止之前。另外可以看出带电粒子能量损失率与介质材料的电子密度成正比,说明具有相同能量的碳离子束入射到不同介质中时,能量损耗的差别,主要取决于介质的电子密度。因此能够推出,能量相同的碳离子束在不同介质中的Bragg峰深度也主要取决于介质的电子密度。
1.2 碳离子束在不同材料中的Bragg峰深度及水等效比(Di)使用SRIM-2013模拟计算能量范围在100~300 MeV/u的碳离子束在水、空气、肌肉及骨骼等效材料中的Bragg峰深度位置。单次模拟的入射碳离子数量为104。
把计算得到的相同能量碳离子束在各等效材料中的Bragg峰深度与相对应能量下碳离子束在水中的Bragg峰深度进行比值,即得到水等效比,具体计算如式3):
| $ {D_i} = \frac{{{D_{media}}}}{{{D_{water}}}} $ | (3) |
其中Di为Bragg峰深度水等效比,Dmedia为一定能量碳离子束在其它等效材料中的Bragg峰深度,Dwater为对应能量碳离子束在水中的Bragg峰深度。
1.3 Bragg峰深度水等效比的验证分别选择能量为200 MeV/u和300 MeV/u的2种碳离子束,再使用SRIM-2013软件计算厚度为4 cm的骨骼等效材料放置在肌肉等效材料中的不同深度时的Bragg峰位置(等效肌肉材料的总厚度设置为30 cm)。采用计算得到的Bragg峰深度水等效比Di,并将此Bragg峰深度转换为水中等效Bragg峰深度。同时在软件中构建厚度为30 cm的水模体,计算对应能量碳离子束在水模体中的Bragg峰深度,并且与水中等效Bragg峰深度进行对比。
1.4 CT值与Bragg峰深度水等效比Di的关系人体组织CT值的差异主要是由于不同组织的电子密度差异所导致。CT值的计算公式见式4)[12]。根据上文所述,碳离子束在不同材料中的Bragg峰深度差异也主要是材料的电子密度不同而造成。因而,可以判断出人体组织CT值与碳离子束在组织中的Bragg峰深度间应该具有内在关联性。选择能量范围在100~300 MeV/u的碳离子束,将其所对应的各等效材料的Bragg深度水等效比Di与CT值,利用Origin 2017进行拟合,研究两者之间的函数关系。
| $ {\text{C}}{{\text{T}}_{{\text{number}}}}{\text{ = }}\frac{{{\mu _{media}} - {\mu _{water}}}}{{{\mu _{water}}}} $ | (4) |
其中CTnumber表示CT值,μ指的是X射线的衰减系数。
2 结 果 2.1 碳离子束Bragg峰的分布特征利用SRIM-2013软件模拟计算了能量范围在100~270 MeV/u内的碳离子束在水中的LET与入射深度关系曲线,结果如图1。从图中可以看到碳离子在射程末端沉积了绝大部分能量形成了尖锐的Bragg峰,并且在峰后离子能量急剧下降为零。另外随着碳离子束入射能量的逐渐增加,Bragg峰深度相应增加,并且展宽也随之增大。这些结果也与文献[13]利用Geant4软件计算结果相一致。

|
图 1 碳离子束在水中的LET与入射深度关系曲线 Figure 1 Curves of linear energy transfer and depth of carbon ion beams in water |
精准得到碳离子束Bragg峰深度是碳离子治疗的关键。基于SRIM-2013软件进一步研究不同能量碳离子束在水中的Bragg峰深度值,结果见图2。模拟得到的结果与文献[14]符合得很好,由此也表明,SRIM-2013软件在模拟碳离子输运上具有可靠的精度。利用Origin 2017软件对模拟计算的数据进行拟合,得到拟合方程为:

|
图 2 碳离子束在水中的Bragg峰深度随入射能量的关系曲线 Figure 2 Curve of Bragg peak depth and incident energy of carbon ion beams in water |
| $ S = A{E^p} $ | (5) |
式中,S为碳离子束在水中的Bragg峰深度,A = 9.3322 × 10−4,E是碳离子束能量,p = 1.7258,R2 = 0.999。
为比较碳离子束与质子束在介质中相同Bragg峰深度处能量沉积的差异,通过SRIM-2013模拟了能量分别为145 MeV/u的质子束和270 MeV/u的碳离子束在水中的LET与入射深度关系曲线,如图3。能够看到碳离子与质子在水中的Bragg峰深度几乎一样,但相较于质子,碳离子的Bragg峰更为锐利,展宽更低。同时能够看到,在相同Bragg峰深度时,碳离子的LET显著大于质子的LET,表明在相同位置处,碳离子沉积的能量更多。因此,在实际治疗肿瘤时,碳离子治疗会比质子治疗的效率更高,治疗周期更短。

|
图 3 碳离子束与质子束在水中LET及入射深度关系曲线 Figure 3 Curves of linear energy transfer and depth of carbon ion and proton beams in water |
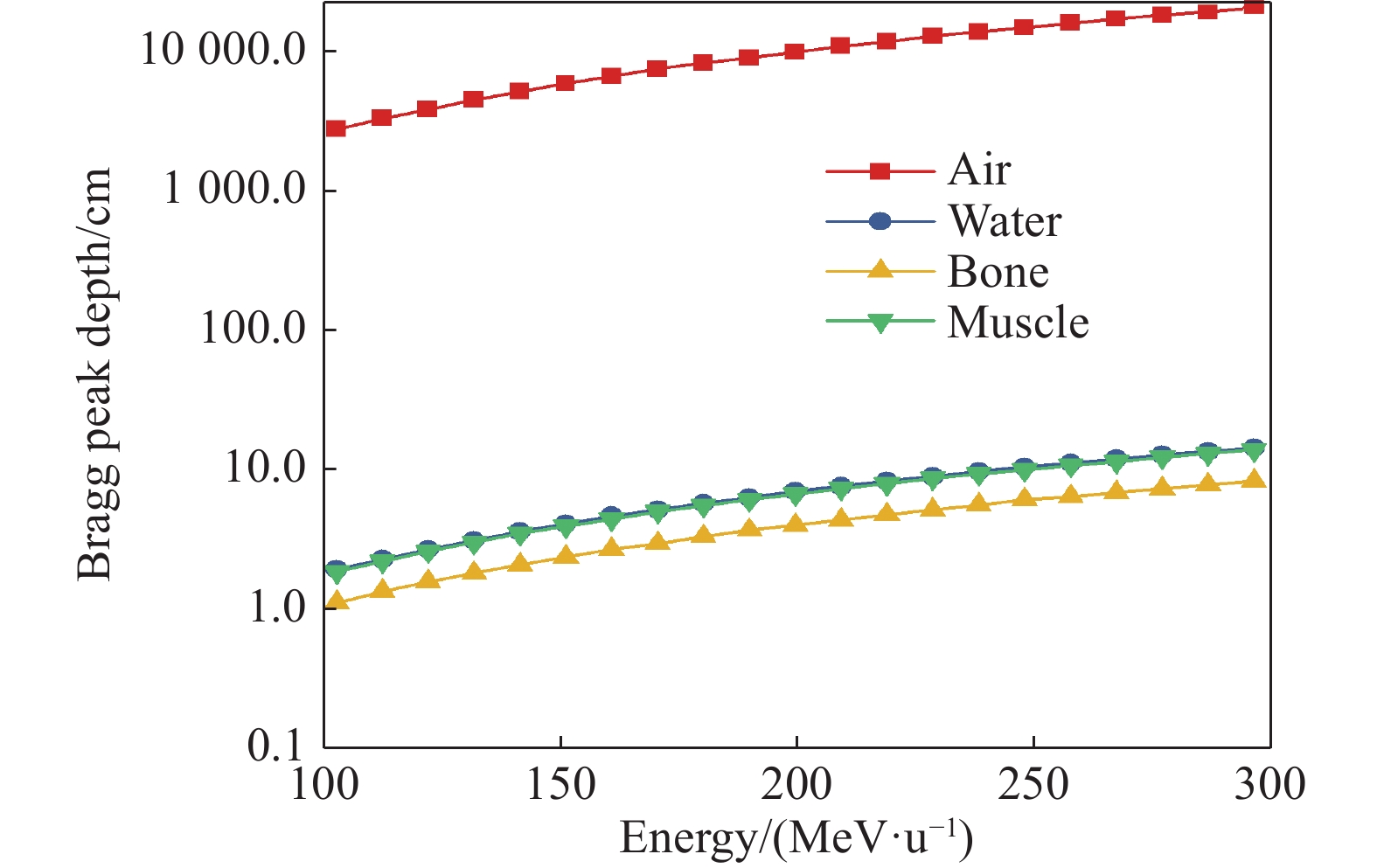
基于SRIM-2013软件模拟计算了能量在100~300 MeV/u的碳离子束在水、空气、肌肉和骨骼等效材料中的Bragg峰深度值,模拟结果如图4。从图中可以看出,在100~300 MeV/u,碳离子束在不同材料中的Bragg峰深度随能量的变化曲线都呈增长趋势。在不同能量下,水与肌肉等效材料两者的变化曲线基本重合。
|
图 4 碳离子束在不同材料中的Bragg峰深度随入射能量的变化曲线 Figure 4 Curves of Bragg peak depth and incident energy of carbon ion beams in different materials |
通过公式3),计算了能量范围在100~300 MeV/u内的碳离子束入射不同材料时的Bragg峰深度水等效比Di。从图5能够看到,随着能量增加,碳离子束在不同材料中的Bragg峰深度水等效比Di几乎没有变化,近似为常数。本研究中碳离子束在空气、肌肉及骨骼等效材料中的Bragg峰深度水等效比Di分别为955.379、0.963和0.595。

|
图 5 不同材料中的Bragg峰深度水等效比Di Figure 5 Water-equivalent Bragg peak depth ratios (Di) in different materials |
为进一步验证Bragg峰深度水等效比Di,使用SRIM-2013软件模拟计算了厚度为4 cm的骨骼等效材料位于肌肉等效材料中的不同深度时,能量分别为200 MeV/u和300 MeV/u碳离子束的Bragg峰深度,计算结果见表1。根据表1数据,可以得到200 MeV/u碳离子束的水中等效Bragg峰深度平均值为8.73 cm,利用软件计算得到水模体中的Bragg峰深度为8.70 cm,误差为0.38%。300 MeV/u碳离子束的水中等效Bragg深度平均值为17.82 cm,软件计算得到水模体中的Bragg峰深度为17.40 cm,误差为2.4%。各能量的碳离子束入射到等效材料中的Bragg峰深度,都能够通过不同材料的Bragg峰深度水等效比转换为碳离子在水中的等效Bragg峰深度。
|
|
表 1 SRIM-2013软件计算结果 Table 1 The results calculated using SRIM-2013 software |
选择在100~300 MeV/u能量范围内的碳离子束在各等效材料中的Bragg峰深度水等效比Di,利用Origin 2017软件将各等效材料的CT值(空气、水、肌肉等效组织和骨骼等效材料CT值分别为−1000,0,40和1000[15])和水等效比Di进行拟合,拟合的方程为:
| $ y = a{e^{x/t}} + b $ | (6) |
其中y为等效材料的Bragg峰深度水等效比Di,x为等效材料的CT值,a = 0.4285,t = −129.7213,b = 0.6046,R2 = 0.999。
随着CT技术快速发展进步,目前的高分辨率CT的空间分辨率能到达0.5 mm以内,能够对人体内肿瘤位置进行精准定位,从而准确获得碳离子束Bragg峰落在肿瘤部位所需的深度。另外通过CT检查技术也能精准计算出人体组织中不同体积单元的CT值。目前,临床中使用的定位CT通常为kV级CT,根据建模时的数据,对不同肿瘤部位选择相应的扫描参数(本单位采用的CT扫描条件:管电压100~140 kV,管电流200~250 mA),从而确定各组织的CT值。通过前述CT值和Bragg峰深度水等效比Di之间的函数关系,计算出人体组织中不同体积单元的Bragg峰深度水等效比Di。进一步,使用得到的水等效比Di把人体组织中不同体积单元的长度转换成水等效长度,再通过公式7)进行加权求和运算,把碳离子束在人体组织中的Bragg峰深度转化为水中等效Bragg峰深度。进而能够利用水中等效Bragg峰深度,反推出碳离子束Bragg峰落在肿瘤部位所需要的能量。因此实现调节碳离子束Bragg峰在组织中的分布,来达到肿瘤精确治疗的目标。
| $ {S_w} = \sum\limits_{i = 1}^n {\frac{{{S_i}}}{{{D_i}}}} $ | (7) |
式中,Sw表示水中等效Bragg深度,Si是碳离子在入射路径上穿过的人体组织中不同体积单元的长度,Di是碳离子在入射路径上穿过的人体组织中不同体积单元的Bragg峰深度水等效比。
3 讨 论由于碳离子束所具备的独特物理和生物特性,近年来,碳离子治疗在肿瘤放射治疗领域展现出较强的优势。和质子相比,碳离子具有更高的LET和生物效应,其对肿瘤细胞DNA的破坏以双链断裂为主,能够对肿瘤造成更大的杀伤效果。另外,相较于氧离子、氮离子和氖离子等其他重离子,碳离子是重离子中原子核质量最轻的,建造相应的重离子加速器更容易,成本更低,具有临床实际应用价值。在碳离子实际治疗过程中,人体非均匀组织会对碳离子Bragg峰的位置分布造成很大影响,确定Bragg峰深度及分布至关重要。得益于计算机技术的快速发展,蒙特卡罗方法在生物医学、计算物理中得到广泛应用。目前在医学物理研究中常使用Geant4、FLUKA、PENELOPE、MCNPX等几种蒙特卡罗软件对粒子在材料中的输运过程进行精准模拟计算。车宇航等[16]通过Geant4模拟计算碳离子束在有机玻璃、铜、铝和铁等多种材料中的深度剂量分布,并得到碳离子束在各材料中的Bragg峰深度与能量的对应关系。Hamad[17]基于Geant4模拟碳离子束入射到水、组织和骨骼上的Bragg峰分布特征。随离子束能量增加Bragg峰的位置转移到模体内更深的位置。Chiriotti等[18]用FLUKA程序模拟碳离子在Bragg峰区域内的微剂量学,并与微型组织等效比例计数器(mini-TEPCs)测量微剂量学光谱数据进行对比研究。
然而上述蒙特卡罗软件操作较为复杂,部分过程需要编写相关程序才能实现模拟,对用户要求较高,需要具备较好的编程能力,对于初学者而言难度较大。SRIM软件操作简便、易学,其起源于1980年,是一个基于DOS的程序,最初被称为TRIM[19]。到了20世纪80年代中期,该软件被Ziegler和Biersack正式开发出来,并得到不断发展和完善。
本研究基于SRIM-2013软件,对100~300 MeV/u能量范围内的碳离子束在不同材料中的Bragg峰分布特性进行了分析。结果显示,对于不同材料,Bragg峰深度水等效比Di近乎为常数,基本不受碳离子束初始入射能量的影响。基于SRIM模拟得到的数据与采用Geant4获得的结果相符合,表明SRIM在模拟碳离子输运上具有较高的精度,满足初学者的使用。水等效比利用人体组织不同体积单元的Bragg峰深度水等效比Di和CT值间的函数关系,能够精确算出Bragg峰落在肿瘤部位所需的水中等效Bragg峰深度,进而反推计算出碳离子束所需的入射能量,由此实现对碳离子束Bragg峰分布的调节,以及对肿瘤的精确治疗。
本研究为碳离子治疗中计算离子入射能量提供了一个新的思路,但仅采用蒙特卡罗软件验证其可行性,另外研究中没有考虑碳离子束的能量展宽,构建的模型较为简单和理想化,实际人体结构非常复杂,还需要在今后实际工作加以完善和进一步验证。
| [1] |
Tinganelli W, Durante M. Carbon ion radiobiology[J]. Cancers, 2020, 12(10): 3022. DOI:10.3390/cancers12103022 |
| [2] |
夏文龙, 胡伟刚, 戴建荣, 等. 粒子治疗技术的进展[J]. 中华放射肿瘤学杂志, 2017, 26(8): 951-955. Xia WL, Hu WG, Dai JR, et al. Progress in charged particle therapy[J]. Chin J Radiat Oncol, 2017, 26(8): 951-955. DOI:10.3760/cma.j.issn.1004-4221.2017.08.022 |
| [3] |
Shiba S, Wakatsuki M, Ohno T, et al. Differences in linear energy transfer affect cell-killing and radiosensitizing effects of spread-out carbon-ion beams[J]. Anticancer Res, 2020, 40(10): 5497-5502. DOI:10.21873/anticanres.14561 |
| [4] |
Suit H, DeLaney T, Goldberg S, et al. Proton vs carbon ion beams in the definitive radiation treatment of cancer patients
[J]. Radiother Oncol, 2010, 95(1): 3-22. DOI:10.1016/j.radonc.2010.01.015 |
| [5] |
Kraft G. Tumor therapy with heavy charged particles[J]. Prog Part Nucl Phys, 2000, 45: S473-S544. DOI:10.1016/S0146-6410(00)00112-5 |
| [6] |
Hosseinzadeh V, Ghaffari H, Rezaeyan A, et al. Estimating organ dose in computed tomography using tube current modulation: a Monte Carlo simulation[J]. Int J Radiat Res, 2021, 19(3): 575-581. DOI:10.52547/ijrr.19.3.575 |
| [7] |
田丽霞, 房冰冰, 朱光昊, 等. 质子束治疗中Bragg峰分布特性的SRIM模拟研究[J]. 中国辐射卫生, 2021, 30(1): 91-93,122. Tian LX, Fang BB, Zhu GH, et al. Simulation on the Bragg peak distribution based on SRIM in proton therapy[J]. Chin J Radiol Health, 2021, 30(1): 91-93,122. DOI:10.13491/j.issn.1004-714X.2021.01.020 |
| [8] |
金潇, 严源, 韩春彩. 高能质子治疗系统辐射环境影响评价关键问题探讨[J]. 中国辐射卫生, 2020, 29(1): 65-68. Jin X, Yan Y, Han CC. Discussion on some key issues in radiation environmental impact assessment of high energy proton therapy system[J]. Chin J Radiol Health, 2020, 29(1): 65-68. DOI:10.13491/j.issn.1004-714X.2020.01.015 |
| [9] |
Ziegler JF, Ziegler MD, Biersack JP. SRIM-The stopping and range of ions in matter (2010)[J]. Nucl Instrum Meth Phys Res Sect B, 2010, 268(11/12): 1818-1823. DOI:10.1016/j.nimb.2010.02.091 |
| [10] |
Zarkadoula E, Toulemonde M, Weber WJ. Additive effects of electronic and nuclear energy losses in irradiation-induced amorphization of zircon[J]. Appl Phys Lett, 2015, 107(26): 261902. DOI:10.1063/1.4939110 |
| [11] |
Grimes DR, Warren DR, Partridge M. An approximate analytical solution of the Bethe equation for charged particles in the radiotherapeutic energy range[J]. Sci Rep, 2017, 7(1): 9781. DOI:10.1038/s41598-017-10554-0 |
| [12] |
Bryant JA, Drage NA, Richmond S. CT number definition[J]. Radiat Phys Chem, 2012, 81(4): 358-361. DOI:10.1016/j.radphyschem.2011.12.026 |
| [13] |
Farina E, Piersimoni P, Riccardi C, et al. Geant4 simulation for a study of a possible use of carbon ion pencil beams for the treatment of ocular melanomas with the active scanning system at CNAO[J]. J Phys Conf Ser, 2015, 664: 072048. DOI:10.1088/1742-6596/664/7/072048 |
| [14] |
Kraan AC. Range verification methods in particle therapy: underlying physics and Monte Carlo modeling[J]. Front Oncol, 2015, 5: 150. DOI:10.3389/fonc.2015.00150 |
| [15] |
赵攀, 宋钢, 林辉, 等. 基于CT值的外轮廓提取方法在精确放疗计划制定中的实现[J]. 中华放射医学与防护杂志, 2007, 27(5): 463-466. Zhao P, Song G, Lin H, et al. Implementation of outside contour extraction based on CT number in making plan of accurate radiotherapy[J]. Chin J Radiol Med Prot, 2007, 27(5): 463-466. DOI:10.3760/cma.j.issn.0254-5098.2007.05.015 |
| [16] |
车宇航, 孟乾乾, 张小芳, 等. 碳离子束射程快速验证方法的蒙特卡罗模拟研究[J]. 原子核物理评论, 2020, 37(4): 901-907. Che YH, Meng QQ, Zhang XF, et al. Monte Carlo study on the method of rapid range verification of carbon ion beam[J]. Nucl Phys Rev, 2020, 37(4): 901-907. DOI:10.11804/NuclPhysRev.37.2019064 |
| [17] |
Hamad MK. Bragg-curve simulation of carbon-ion beams for particle-therapy applications: a study with the GEANT4 toolkit[J]. Nucl Eng Technol, 2021, 53(8): 2767-2773. DOI:10.1016/j.net.2021.02.011 |
| [18] |
Chiriotti S, Conte V, Colautti P, et al. Microdosimetric simulations of carbon ions using the Monte Carlo code FLUKA[J]. Radiat Prot Dosim, 2018, 180(1/4): 187-191. DOI:10.1093/rpd/ncx201 |
| [19] |
Biersack JP, Haggmark LG. A Monte Carlo computer program for the transport of energetic ions in amorphous targets[J]. Nucl Instrum Meth, 1980, 174(1/2): 257-269. DOI:10.1016/0029-554X(80)90440-1 |




