单光子发射计算机断层显像(Single-Photon Emission Computed Tomography, SPECT)提供了一种非侵入性方法,得知人体任意角度断层面的放射性浓度分布,用于在解剖学变化发展之前并且通常在临床症状出现之前检测早期病理生理学变化[1]。SPECT断层显影在疾病诊断方面发挥了重要作用,但与其他普通放射诊断仪器相比,其空间分辨率低,难以得到精确的解剖结构和立体定位[2]。影响SPECT断层图像的空间分辨率除了有准直器的性能、重建算法等因素有关外,其旋转几何中心与矩阵中心轴不一致也会对重建的断层图像造成影响[3],探头的旋转中心是指探头的机械旋转中心,它应该与图像重建矩阵中心相一致,如果两个中心不重合,称为旋转中心漂移[4]。
如不进行恰当的修正将可能在断层图像中造成伪影[5]。因此有必要定期对SPECT进行旋转中心漂移性能的检测。目前国际原子能机构(International Atomic Energy Agency, IAEA)、美国医学物理学家协会(American Association of Physicists in Medicine, AAPM)、美国电气制造商协会(National Electrical Manufacturers Association, NEMA)发布的报告与标准涉及到旋转中心漂移的算法一共有两种,一种是曲线拟合法,一种是算术平均法[6-8]。
本研究以AAPM REPORT NO.22为基础,采用一个点源,研究曲线拟合法与算术平均法在双探头旋转中心漂移计算中的差异,并与厂家计算结果的通过性进行比较,比较得出哪种算法更适用于评价市面上各种机型的旋转中心性能,为相关标准的制定提供参考。
1 材料与方法 1.1 研究对象选择全国范围内9台双探头SPECT设备,地域范围覆盖北京、河北、陕西、广东。本次实验用SPECT设备的生产厂家有3家,分别为美国通用电气公司(GE)、荷兰飞利浦公司(Philips)和德国西门子(Siemens)公司。为了便于数据的比较,将这3家公司按照抽签的方式依次编号为A、B、C厂家。其中A厂家5台,B厂家3台,C厂家1台。每台设备都有两个探头,对数据进行筛选和缺失值去除,最后得到9台设备中13个探头的数据,将探头从1到13进行编号。
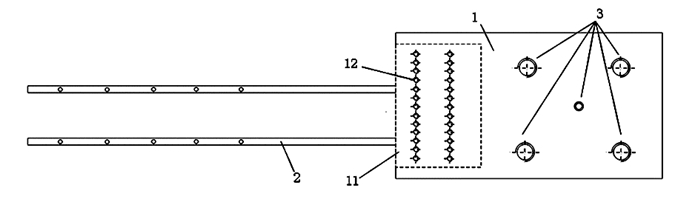
1.2 仪器设备点源支架模体,该模体能够完成多种组合的点源摆放,其结构如图 1、图 2所示。其中1为模体主体,2为若干矫正尺,3为水平调节组件,水平调节组件3保持整个模体处于水平状态,模体主体1的一端上有刻度11,最小单位为毫米(mm),矫正尺2一端与模体主体1的一端连接,并可在水平方向上左右移动,找到目标位置后用螺栓12固定住,矫正尺上有若干圆孔21,点源置于圆孔中。本实验因用一个点源,所以仅用到一根矫正尺。经多次实验验证,该模体的准确性与重复性较好,可完成本实验的测量。
|
图 1 实验模体俯视图 |

|
图 2 实验模体主视剖面图 |
根据AAPM REPORT NO.22报告提供的方法进行点源摆放,将实验模体组合好然后摆放于机床上,调整探头旋转半径为20 cm;将99mTc标记的放射性药物制得的点源放入0.5 ml试管内,活度约为37 MBq、体积约为0.1 ml;将装好点源的试管套入模体前方的尺子孔里,移动模体尺子,使得点源与旋转轴偏离5 cm;设置采集图像矩阵大小为256×256,每6度一帧,每帧采集10秒。
然后按照每个厂家规定的旋转中心漂移测量方法进行模体的摆放,用厂家自带的软件对其结果进行测定,并将结果记录,作为以上两种方法的对照。
1.3.2 图像的分析用Java代码编写插件程序,用ImageJ软件加载插件,根据重心坐标法计算每幅Dicom图像里点源的坐标,得到每个点源的X方向坐标值。X方向的重心坐标公式如式(1):
| $ COGX = \frac{{\sum\nolimits_{i = {i_1}}^{i = {i_n}} {\sum\nolimits_{j = {j_1}}^{j = {j_n}} i \times MATRIX(i, j)} }}{{\sum\nolimits_{i = {i_1}}^{i = {i_n}} {\sum\nolimits_{j = {j_1}}^{j = {j_n}} {\;\;MATRIX(i, j)} } }} $ | (1) |
COGX-点源在图像上重心坐标的x值; i-为x方向的像素索引; j-为y方向的像素索引; MATRIX(i, j)-为像素块的像素值。
1.3.3 数据的计算(1) 曲线拟合法
本拟合方法用MATLAB软件,采用最小二乘法对数据进行拟合。MATLAB是集数值计算、符号计算和图形可视化于一体的功能强大和操作简单的应用软件,其中MATLAB曲线拟合工具箱拥有一个可视化的图形界面[9],通过cftool命令进入曲线拟合工具箱主界面,可以使用随带的函数模型库进行拟合分析,也可以指定自行定义的方程式对数据进行拟合,使其使用范围更广[10]。曲线拟合就是找出一条光滑曲线,这条曲线要能够反映出一组离散数据的变化趋势,使数据误差的平方和最小,但不要求拟合的曲线经过每个点,这就是最小二乘法曲线拟合。
打开曲线拟合工具箱,将旋转的角度为横坐标轴,点源的横坐标值为纵坐标轴,用MATLAB软件对曲线进行拟合,拟合方程为:
| $ y = a \times \mathit{sin}(b \times x + c) + d $ | (2) |
x-探头旋转的角度; y-点源在图像上重心坐标的x值; a-曲线拟合振幅; b-曲线拟合频率; c-曲线拟合相位; d-曲线在y轴的上下位置。
d值为最佳拟合旋转中心,将其与图像矩阵的中值相减,得到漂移像素个数,将漂移的像素个数乘以每个像素的大小,得到以毫米为度量单位的平均漂移值,即旋转中心漂移的大小。
(2) 算术平均值法
根据公式(3)计算每幅图像点源x方向重心坐标平均值
| $ C O R=\frac{1}{N_{v}} \sum_{j=1}^{N_{v}} X_{j} $ | (3) |
COR-点源在幅图像上重心坐标x值的平均值; Xj-点源在第幅图像上重心坐标的x值; Nv-图像的数量; j-图像的次序。
| $ \delta COR = abs(COR - {X_{cen}}) $ | (4) |
| $ {X_{cen}} = \frac{{N - 1}}{2} $ | (5) |
δCOR-点源漂移的平均像素数; Xcen-图像矩阵的中心; N-矩阵的大小。
1.3.4 统计学处理采用SPSS 22.0软件进行分析。所有数据均进行正态性检验符合正态分布。分别对曲线拟合法计算结果与算术平均法计算结果、曲线拟合法计算结果与厂家计算结果、算术平均法计算结果与厂家计算结果进行配对t检验。P<0.05为差异有统计学意义。
2 结果本研究采用三个厂家的13个探头,分别通过曲线拟合法与算术平均法计算SPECT探头旋转中心的漂移值,与此同时,用厂家自带软件实时获取探头旋转中心的漂移值。各探头两种计算方法结果及厂家计算结果列于表 1。曲线拟合法计算结果与算术平均法计算结果之间比较,两组数据差异无统计学意义(t=2.20, P=0.84, P>0.05),曲线拟合法计算结果、算术平均法计算结果分别与厂家计算结果之间比较,两组数据差异均无统计学意义(t=1.79, P=0.50, P>0.05;t=1.79,P=0.53,P>0.05)。
|
|
表 1 三种方法测得探头的旋转中心漂移值 |
由于不同厂家设定的合格值不一,因此将探头按照厂家分类,将两种算法计算值的通过性分别与厂家进行比较,结果列于表 2,其中“+”代表通过,“-”代表不通过。结果发现曲线拟合法计算结果、算术平均法计算结果与厂家的通过性均一致。
|
|
表 2 三种算法测得探头的旋转中心漂移值的通过性 |
曲线拟合法与算术平均法是计算SPECT探头旋转中心的两种方法,本研究采用一个点源,就这两种算法计算的平均旋转中心漂移值进行了比较,结果表明两种计算方法得到的计算结果差异无统计学意义,并将两种方法的计算结果分别与厂家计算结果之间比较,两组数据差异均无统计学意义,其通过性也一致。在我国医疗系统中,SPECT设备的厂家来源主要有GE公司、Philips公司和Siemens公司,但是他们对于旋转中心的检测方法各不相同。GE公司采用一个点源,在调用旋转中心检测的软件后,两个探头的采集图像界面分别会出现两个圆框,将点源图像置于圆框内便可进行检测;Philips公司同样采用一个点源,点源放置于特定的三脚架上并稍微偏离旋转轴;Siemens公司采用五个点源,点源放置于特制的旋转中心模体上。不同的厂家旋转中心漂移检测方法不一,其计算方法与图像处理也无从所知。Blue等[11]研究中,使用1个点源分别在5个位置进行旋转中心测试,结果表明,只要点源能均匀地在探头范围内成像,点源的位置对于旋转中心的测量影响不大,但是Harkness等[12]建议点源不应精确地放置在旋转轴(AOR)上,而应该稍微偏离旋转轴中心进行测量。因此本研究就AAPM REPORT NO.22报告的实验条件,采用一个点源对探头旋转中心进行检测,且点源与旋转轴偏离5 cm。
本研究中,探头围绕点源旋转360°,每6°采集一幅图像,一共可采集60幅图像,每幅图像都能计算出点源在x方向的坐标值,一共可得到60个坐标值,无论点源摆放的位置如何,都符合这样一条规律:如果不存在旋转中心的漂移,则60个坐标值的平均值应该就是图像矩阵的中心。在采用曲线拟合法计算当中,以探头旋转的角度为横坐标、对应点源的x方向坐标值为纵坐标作图,采用最小二乘法对各点进行曲线拟合,会得到一条符合正弦曲线变化规律的一条曲线,求出曲线的参数,其d值就为曲线的中值,将中值与图像矩阵中心值相比,其偏差就为该探头平均漂移的像素值;采用算术平均法则不需要做图,直接将计算得出的60个坐标值进行算术平均,再将算术平均值与图像矩阵中心作差,其偏差就为该探头平均漂移的像素值。本研究结果表明,两种计算方法得到的计算结果差异无统计学意义,但将两种计算过程加以引申,发现有如下规律:(1)若数据出现离群值,则采用算术平均法会出现较大差异;(2)曲线拟合法将每幅图像的实际值与计算值呈现于一幅图像上,便于后续的矫正时的观察与分析;(3)如后续计算探头的倾斜,即y方向的漂移值,根据国标(GB/T 18988.2-2013)[13],则需要拟合曲线的振幅a参与计算。综上所述,在两种算法结果差异无统计学意义的前提下,本研究更倾向于采用曲线拟合法。由于本实验的实验对象有限,期待未来能够增加实验数据,进一步对两种算法的差异进行比较。
由于SPECT成像的特殊性,其成像过程如下:(1)光子进入探测器的方向由探头前的准直器控制,准直器能影响设备的系统空间分辨率;(2)接着穿过准直器孔的光子将撞击闪烁晶体,光子与闪烁晶体相互作用并在整个晶体结构中沉积能量;(3)发射的闪烁光子被引导向一组多个光电倍增管(PMT),每个PMT产生与闪烁光的强度成比例关联的电信号。当组合来自多个PMT的各个能量信号,并假设知道每个PMT在x、y坐标系中的绝对位置时,可以通过计算重心坐标来确定相当准确的事件位置[14]。鉴于此,点源在探测器的成像具有统计涨落特性,在同样的实验条件和同样的实验机器条件下,前后两次检测得到的数据都会有些许差异,因此本研究在对旋转中心漂移数据进行定量比较的同时,还采取了与厂家的通过性进行比较,发现两种计算方法的计算结果与厂家计算结果比较,通过性与厂家均一致,可初步认为两种计算方法均适合于各厂家。
多年来,SPECT在混合成像系统中越来越多地与CT结合[15], 与此同时,PET与MR的结合正在进行临床评估,而SPECT与MR由于其对物理准直的额外要求仍在开发中[16],SPECT图像与其它成像系统的图像需要进行图像融合,这要求SPECT自身重建图像应对病灶提供更为准确的位置。图像重建算法都是按照精确的圆轨道扫描推导出来的,并默认机械坐标系、探头电子坐标系和重建图像坐标系相互重合。实际的扫描机架和电子学系统总存在误差,具体表现为图像变得模糊放大,或发散成环状伪影。这提示旋转中心的漂移在SPECT性能检测中的重要性。
本研究就AAPM REPORT NO.22报告提供的方法,采用统一的实验条件、统一的实验点源活度与摆放方式,对两种计算方法进行了比较,为后续标准的制定提供了参考意见。
利益冲突
本人与本人家属、其它研究者,未因进行该研究而接受任何不正当的职务或财物利益,在此对研究的独立性和科学性予以保证。
| [1] |
Pacilio M, Lauri C, Prosperi D, et al. New SPECT and PET Radiopharmaceuticals for Imaging Inflammatory Diseases:A Meta-analysis of the Last 10 Years[J]. Seminars in Nuclear Medicine, 2018, 48(3): 261-276. DOI:10.1053/j.semnuclmed.2017.12.004 |
| [2] |
Zeng G L, Gagnon D. CdZnTe strip detector SPECT imaging with a slit collimator[J]. Physics in Medicine and Biology, 2004, 49(11): 2257-2271. DOI:10.1088/0031-9155/49/11/010 |
| [3] |
Jaszczak R J, Coleman R E, Whitehead F R, et al. Physical Factors Affecting Quantitative Measurements Using Camera-Based Single Photon Emission Computed Tomography (Spect)[J]. IEEE Transactions on Nuclear Science, 1981, 28(1): 69-80. DOI:10.1109/TNS.1981.4331143 |
| [4] |
张永学. 核医学[M]. 北京: 科学出版社, 2003.
|
| [5] |
Dezarn W A. Quality assurance issues for therapeutic application of radioactive microspheres[J]. International Journal of Radiation Oncology Biology Physics, 2008, 71(1). |
| [6] |
International Atomic Energy Agency, Quality Assurance for SPECT Systems[S].Vienna: IAEA Human Health Series No. 6, IAEA, 2009.
|
| [7] |
American Association of Physicists in Medicine, Rotating Scintillation Camera SPECT Acceptance Testing and Quality Contro[S].New YORK: AAPM report no.22, AAPM, 1987.
|
| [8] |
National Electrical Manufacturers Association, Performance Measurements Pf Gamma Cameras, NEMA Standards Publication Nu 1-2007, NEMA, rosslyn(2007).
|
| [9] |
Zhou Y F, Tham L G, Yan R W M, et al. The mechanism of soil failures along cracks subjected to water infiltration[J]. Computers & Geotechnics, 2014, 55(2): 330-341. |
| [10] |
Massey C I, Petley D N, Mcsaveney M J. Patterns of movement in reactivated landslides[J]. Engineering Geology, 2013, 159(12): 1-19. |
| [11] |
Blue P W. Accuracy of Center of Rotation Determination for SPECT Imaging[J]. 1989.
|
| [12] |
Harkness BA, Rogers WL, Clinthorne NJ, et al. SPECT: Quality control procedures and artifact identification. J Nuc/Med Techno/1983; Ⅱ: 55-60.
|
| [13] |
国家质量监督检验检疫总局. GB 18988.2-2013放射性核素成像设备性能和试验规则第2部分: 单光子发射计算机断层装备[S].北京: 中国标准出版社, 2013.
|
| [14] |
Drzezga A, Souvatzoglou M, Eiber M, et al. First clinical experience with integrated whole-body PET/MR:comparison to PET/CT in patients with oncologic diagnoses[J]. Journal of Nuclear Medicine, 2012, 53(6): 845. DOI:10.2967/jnumed.111.098608 |
| [15] |
Ljungberg M. Absolute Quantitation of SPECT Studies[J]. Seminars in Nuclear Medicine, 2018, 48(4): 348. DOI:10.1053/j.semnuclmed.2018.02.009 |
| [16] |
Livieratos L. Technical Pitfalls and Limitations of SPECT/CT[J]. Seminars in Nuclear Medicine, 2015, 45(6): 530-540. DOI:10.1053/j.semnuclmed.2015.06.002 |




