国际放射防护委员会ICRP78号出版物里指出工作人员吸入摄入钚的常规监测方法有:活体测量、离体测量和个人空气采样测量。采用离体测量方法,测量排泄物中的钚具有更高的灵敏度,因此离体测量是钚个人剂量监测的基本方法。常用的离体测量方法为测量分析尿液样品中的钚放射性核素的活度,由排泄方程计算工作人员初始摄入量,根据ICRP参考数据估算钚所致的内照射剂量。单独的尿钚测量分析过程耗时长,且还有无法解释摄入途径和吸入粒子在人体内被吸入血液的份额等问题。这些问题将直接导致离体测量评估钚内照射剂量不确定度大,因此针对工作人员吸入钚的个人常规监测只采用离体测量是不充分的。
个人剂量监测中活体测量可以快速、直接测量工作人员体内放射性核素的含量。肺部计数器直接测量体内239Pu衰变发射的X射线(Lα13.6 keV,Lβ17.6 keV,Lγ20.2 keV)灵敏度低。据调研结论,纯钚在肺内的最低可测量活度约为2.4 kBq[1],并且这个值随被测量个体胸壁厚度的不同差异巨大,因此以直接测量人体肺部钚含量作为工作人员吸入钚常规监测是不合适的。
燃料循环过程的中的钚往往混合着241Am,241Am是由241Pu通过β衰变得到,59 keV能量的γ射线发射率为36%,相对于钚同位素发射的低能X射线更易被探测到。将241Am作为钚同位素在人体肺部的示踪核素,有利于提高胸壁外测量钚的探测下限。现有的肺部计数器测量241Am最低可测量活度能够达到10 Bq以下[1],远远低于同等条件下测量肺内钚的最低可测量活度。
本文旨在以241Am作为测量肺内钚的是替代核素,由活体测量工作人员体内的241Am含量来估算工作人员吸入后短期肺部钚的含量及致内照射剂量。
1 资料和方法 1.1 计算模型参数放射性核素进入人体后,除了发生放射性衰变外,还会经历沉积、转移、吸收、排泄等一系列过程,这些过程与摄入物质的物理、化学特性,人体的器官、组织构造和功能有关。对接触放射性物质的工作人员,ICRP已发布一系列描述通过吸入、食入进入人体内的放射性核素的行为模型。本文采用ICRP 66/67报告[2-3]提出人体吸入钚/镅气溶胶生物动力学模型。
用241Am作为吸入钚的示踪核素关键问题在于:241Am和钚类核素被人体吸入后在肺组织中的比例是变化的还是保持一致的;核设施生产钚同时,钚的各同位素在混合物中所占比例是否确定。关于第一点,241Am的溶解度与钚氧化物溶解度的相似性已经在大鼠实验上得到验证,可认为镅钚进入人体肺部短时间内比例保持不变[4];关于第二点,本文建立的算法给出了一定的假设。
钚同位素和241Am在进入人体后的行为还受到它们各自化合物气溶胶颗粒的影响,对其描述需要选择合适的模型参数。假设含有M型钚氧化物的气溶胶是由中子照射238U产生的锕系核素分离得来,各核素组成的参数描述如下:
m:新分离出时(ta=0),241Pu与239Pu的活度比;f:239Pu的活度占所有α衰变钚类核素(238Pu、239Pu、240Pu)活度的比值;ta:浓缩提纯钚同位素所用的时间,它决定了钚同位素中241Pu和241Am的组份比;这里m、f、ta为单独一次分离操作参数。
ne:241Am与239Pu的活度比,这里的241Am是由241Pu衰变而来;me:241Pu与239Pu的活度比;fe:239Pu与所有α衰变钚类核素的活度比;其中,ne、me、fe中涉及的钚同位素主要来源于分离工艺设备和管道内积留的放射性污染,它们的值取决于分离设备的使用时间(Te)。
此处无法确切知道这些时间参数的值,假设大致范围为:0.001≤m≤0.01,0 ≤ta≤40年,0 ≤Te≤40年,0.5≤f ≤1.0。此外中子辐照铀除产生钚以外还会产生镅,分离钚的程序还可能存在除镅工艺,本文暂不考虑这部分镅组分变化的影响。
1.2 活度与剂量计算使用上述参数与假设,当气溶胶中239Pu含量为1 Bq时,可以用以下方程来描述气溶胶中241Am、241Pu和所有α衰变钚类核素的活度:
| $ \begin{gathered} {A_{Am- 241}}\left( {m, {t_a}, {n_e}} \right) = \varphi m\left[{{e^{-\left( {0.693/432.2} \right) \cdot {t_a}}}} \right. \hfill \\ \left. {-{e^{-\left( {0.693/14.4} \right) \cdot {t_a}}}} \right]\frac{{432.2}}{{432.2 -14.4}} + \left( {1 -\varphi } \right){n_e} \hfill \\ {A_{pu -241}}\left( {m, {t_a}, {n_e}} \right) = \varphi m{e^{ - \left( {0.693/14.4} \right) \cdot {t_a}}} + \left( {1 - \varphi } \right){m_e} \hfill \\ {A_{\Sigma pu}}\left( {f, {f_e}} \right) = \frac{1}{{\varphi f + \left( {1 - \varphi } \right){f_e}}} \hfill \\ \end{gathered} $ |
这里的含有钚镅核素的放射性气溶胶有两个来源,一是正在进行分离操作的钚,二是分离装置中积留的钚,φ表示气溶胶中钚来源于分离操作所占的比例,由于这两个来源的钚随机混入空气中,因此φ可取0~1任意值。
在单次吸入摄入上述组分的气溶胶后t时刻肺中241Am的活度:
Am肺Am-241(t, AMAD)=AAM-241(m, ta, ne)AmAmAm-241(t, AMAD)+Apu-241(m, ta, me)AmAmAm-241(t, AMAD)
此处AAmpu-241(t, AMAD)、AAmAm-241(t, AMAD)是一次吸入摄入1 Bq,吸入类型M的241Pu或241Am气溶胶后,t时刻内肺部241Am的活度,相当于滞留系数。
相应的一次吸入上述气溶胶后的有效剂量表示为:
| $ \begin{gathered} {E_{50}}\left( {m, {t_a}, {m_e}, {n_e}, \varphi, AMAD} \right) = {A_{Am-241}}\left( {m, {t_a}, {n_e}} \right) \hfill \\ e_{50}^{Am-241}\left( {AMDA} \right) + {A_{pu-241}}\left( {m, {t_a}, {n_e}} \right)e_{50}^{pu - 241}\left( {AMDA} \right) + \hfill \\ {A_{\Sigma pu}}\left( {f, {f_e}} \right)e_{50}^{pu - 239}(AMDA \hfill \\ \end{gathered} $ |
其中,e50m(AMDA)是由一次吸入摄入1 Bq,吸入类型为M的241Am、241Pu或239Pu的气溶胶放射性活度到工作人员待积有效剂量E50的转换系数。
函数AAmpu-241(t, AMAD),AAmAm-241(t, AMAD),e50Am-241(AMDA),e50pu-241(AMDA),e50pu-239(AMDA),采用ICRP 66、67号报告提出的吸入类型M的钚和镅的生物动力学模型,使用Leggett提供的计算方法[5]。因计算关注人员吸入钚后短期内的辐射剂量问题,此处对吸入241Pu入肺后衰变生成的241Am不予考虑。
2 结果 2.1 算法结论分析由本文提出的方程可以看出工作人员吸入的气溶胶内放射性核素组成主要依赖于两组参数:1)m、ta和f,它们被用来描述进行分离操作中的钚;2)me、ne和fe,它们被用来描述分离装置积留的钚。参数φ则用来描述气溶胶中钚的两种来源的所占的比例。参数me,ne,fe取决于分离设备使用的总时间,它们的值可以假设为在设备运行时间内(Te)一个随机值(0<φ<1)乘以设备壁沉积的钚的量(由参数tai,mi,fi表示):
| $ {n_e} = \frac{{\sum\nolimits_{i = 1}^N {{\varphi _i}{A_{Am-241}}\left( {{T_e}\frac{i}{N} + {t_{ai}}, {m_i}} \right)} }}{{\sum\nolimits_i^N {{\varphi _i}} }} $ |
| $ {m_e} = \frac{{\sum\nolimits_{i = 1}^N {{\varphi _i}{A_{Pu-241}}} \left( {{T_e}\frac{i}{N} + {t_{ai}}, {m_i}} \right)}}{{\sum\nolimits_i^N {{\varphi _i}} }} $ |
| $ {f_e} = \frac{{\sum\nolimits_{i = 1}^N {{\varphi _i}{f_i}} }}{{\sum\nolimits_i^N {{\varphi _i}} }} $ |
由公式可知,参数me,ne,fe的值决定于参数mi,tai,fi和Te的值,而后者的值如之前所述,是在一个范围内变化的。因此,先前处理的钚的参数值(tai,mi,fi)、设备运行时间(Te)、正在处理的钚的参数值(ta,m,f)、每种来源所占气溶胶内放射性含量的比例(φ)、粒子分布参数(AMAD)共同构成了肺部241Am活度含量和有效剂量估值的计算模型。可以通过计算模型中的每个单独参数的不确定度来分析算法的可靠性。参数不确定度分析包括每个参数概率分布分析,使用Monte Carlo模拟技术对算法模型的精度进行计算。本文采用MATLAB产生随机数,对应特定活度和剂量估算值,针对每个参数概率分布进行随机抽样以确定一套参数值。重复这个过程多次,以产生一个合适的分布方案。
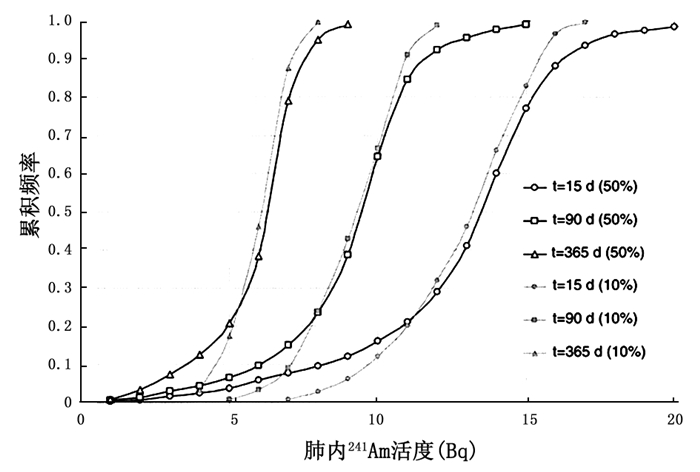
3 讨论图 1显示在一次监测活动中,肺中241Am的活度分布函数。可以当作是有效剂量为20 mSv情况下,单一摄入M型钚气溶胶的情况。图 1中各参数分布在一定范围内取平均值:tai=ta=10,mi=m=10,fi=f=0.75,AMDA=5 μm,相对标准偏差(δ)为10%和50%。分离设备运行时间Te取值40年,ne的计算值为0.25±0.02。图 1曲线显示,在单独一次吸入241Am 15、90、365天后,所有参数取值中有98%、96%和87%的参数取值(δ= 50%)将会使肺内241Am活度的计算值大于肺部计数器对241Am的最低可测量的活度值(MDA=4 Bq)。如果参数值在一个更窄的范围内变化(δ= 10%),相应的百分比会更高。这意味着在许多实际情况下,定期测量肺部的241Am将能够用来监测在ALI水平下单一次吸入钚短期内肺部的滞留量。
|
图 1 采用Monte Carlo确定一套参数生成肺内241Am活度评价的累积频率函数 |
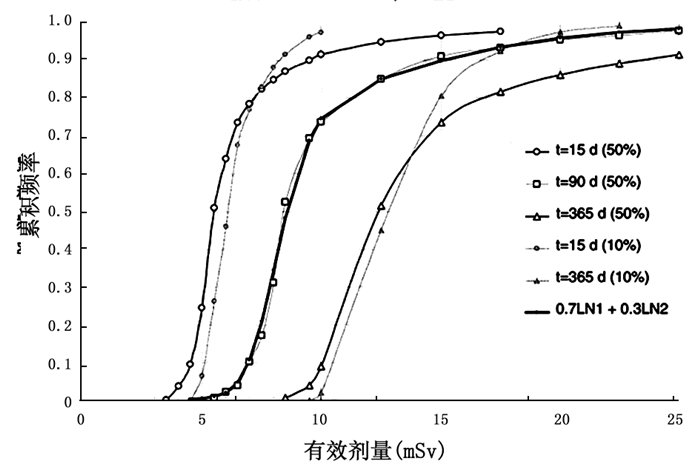
假设一次吸入M型气溶胶15、90、365天后测得肺部241Am活度为4 Bq,且表示气溶胶成分的各参数值同图 1。图 2中,90天,δ取50%处实线为一个假设分布,表示两个对数正态分布函数叠加,中值取8.2 mSv(占70%)和12.5 mSv(占30%),几何标准偏差分别为1.14和1.55。95%置信区间为0.27 mSv(6.14/23.0),最佳估算有效剂量值E=11.9 mSv,比E0=8.85大1.35倍,这里的有效剂量的估算由各参数的平均值得来。
|
图 2 系列参数概率分布的标准偏差对有效剂量估算的影响 |
文章介绍了一种通过肺部计数器测量肺内241Am活度值采用数值方法来估算工作人员肺部钚含量及致内照射剂量的方法。结果表明,使用肺部计数器常规测量人体肺部241Am活度来估算一次独立吸入ALI水平内的钚的可行性,为估算处理钚的工作人员的个人剂量监测提供一定的方法支持,对判断接触钚的工作人员是否需要进行针对吸入钚的促排治疗提供一定的依据。
| [1] |
International Commission on Radiological Protection. Individual Monitoring for Internal Exposure of Workers. ICRP Publication 78[P]. 2005.
|
| [2] |
International Commission on Radiological Protection. Human Respiratory Tract Model for Radiation Protection (Oxford: Pergamon Press) ICRP Publication 66[P]. ICRP, 1993, 24(1-3).
|
| [3] |
International Commission on Radiological Protection. Age-dependent Doses to Members of Public from Intake of Radionuclides: Part 2. Ingestion Dose Coefficients (Oxford: Elsevier Science) ICRP Publication 67[P]. Ann. ICRP 23(3/4), pp 121-139 (1993).
|
| [4] |
Ishigure N, Enomoto H, Nakano T, et al. Validity of 241Am as a Tracer of Inhaled Pu in External Chest Counting[J]. Radiat. Prot Dosim, 1998, 79(1-4): 133-136. |
| [5] |
Leggett R W, Eckerman K F, Williams L R. An Elementary Method for Implementing Complex Biokinetic Models[J]. Health Phys, 1994, 64(3): 260-271. |


