1 概述

随着生产和科学技术的进步, 对检测数据的准确可靠性提出了更高的要求。过去通常用测量误差即测量结果与真值的差异来表示测量结果的准确可靠程度, 但由于真值通常是未知的, 所以误差常常也无法知道, 只能用约定真值代替真值来求误差。在实际工作中更多遇到的应该是测量的不准确度, 这已逐渐成为人们的共识。特别是由于国际贸易的发展, 检测数据的质量高低需要在国际间得到评价和承认, 由此开展的国际间的验证比对试验、实验室认可等活动, 越来越重视对测量结果不确定度的分析和表达。国家标准《校准和检验实验室能力的通用要求》(GB/T15481 -1995, 等同采用ISO导则25)中就要求实验室的每个证书或报告, 均应对估算的校准和测试结果的不确定度作出说明:ISO 9001也规定, 应保证所用设备的测量不确定度已知。在1993年, 由BIPM(国际计量局)、IEC(国际电工委员会)、IFCC(国际临床化学联合会、ISO(国际标准化组织)、IUPAC(国际理论与应用化学联合会)、IUPAP(国际理论与应用物理联合会)和OIML(国际法制计量组织)等7个国际机构共同发起, ISO公布了“测量不确定度表示指南”, 从而形成了共同的基础。

2 基本概念 2.1 测量不确定度

它是一个与测量结果相关的参数, 用以表征可以合理赋予被测量值的分散性。该参数可以用标准偏差或其给定倍数来表示, 也可以用置信水平的区间半宽度来表示。测量不确定度通常由其所有的不确定度分量构成, 其中有些分量可以用测量结果的统计分析来加以评定, 有些分量则基于统计分析以外的方法或信息来评定。测量不确定度一般来源于随机性和模糊性, 前者来自一些主客观条件不充分, 后者归因于事物本身概念不明确。在具体实践中, 可能包括的来源如下:

(1) 对被测量的定义不完善;

(2) 实现被测量的定义的方法不理想;

(3) 被测量的样本(抽样)不能代表所定义的被测量;

(4) 环境条件的测量不完善, 或对测量受环境条件影响的认识不周全;

(5) 人员对模拟仪器的读数有偏差;

(6) 测量仪器的分辨力和鉴别阈不够;

(7) 赋予计量标准的值和标准物质的值不准;

(8) 从外部来源取得, 并用于数据计算的常数和其他参数不准;

(9) 与测量方法和测量程序相关联的近似性和假定性;

(10) 在表面上完全相同的条件下, 被测量重复观测值的变化。

2.2 不确定度的分类

如上所述分为两类:一类是通过对测量结果的数据列进行统计分析, 由概率密度函数求其频率分布加以评定得到的不确定度, 称为统计不确定度分量, 或者“A类不确定度分量”; 另一类是通过非统计的其他方法或信息, 如基于对事件发生的信任程度或经验得到的假定概率分布加以评定, 称为非统计不确定度, 或者“ B类不确定度分量”; 两者都可用标准偏差表示。应当指出的是:测量误差可以分为系统误差和随机误差; 但不确定度分成A类和B类, 并不与之相互对应, 系统效应修正值的不确定度可能由A类、也可能由B类得到。

2.3 标准不确定度和展伸不确定度

用标准差表示的测量结果不确定度, 通常称为“标准不确定度” u; 当一个测量结果由若干个其他量求得时, 这个测量结果的标准不确定度, 就等于这些其他量的方差或协方差之(加权)和的正平方根, 称之为“合成标准不确定度” u_c; 但在安全、健康等领域, 为了提高不确定度的置信水平, 可将合成标准不确定度乘以一个数值因子K, 由此得到“展伸不确定度”或“范围不确定度” U = ku_c, 它表示测量结果附近的一个置信区间, 且可以合理地认为(或赋予)被测量值将以较高的置信概率落于该区间中; 上述数值因子k通常称为“包含因子”或“范围因子”。

2.4 自由度

计算加和的项数减去对加和结果的限制数

3 测量不确定度的评定

在评定不确定度时, 其流程如附图所示。大致分为以下几步:①建立数学模型; ②A类或B类不确定度的评定; ③不确定度的合成或汇总; ④计算总不确定度; ⑤不确定度的报告。

假设被测量Y不能直接测得, 而是通过函数关系f(X_i), 从N个别的量X_i得来, 即   Y=f(X₁, X₂, …X_n)

其中X_i称为输入量, Y称为输出量。

对Y和X_i的最佳估计值分别为y和x_i, 则测量结果y可以表示为:

这时, 不确定度的传播系数δf/ δx_i, 表示x_i变化一个单位量时引起y的变化量。所谓建立数学模式, 目的是由各个X_i分量的标准不确定度u(x_i)汇总成Y的合成不确定度u_c时, 确定其相应的传播系数δ_f/ δx_i, 并有u_i =|δ_f/ δx_i|u(x_i)

4 标准不确定度的A类评定 4.1 一个量的等精度独立测量

对于量X_i的n次等精度独立测量, 得到一系列数值为:x_i1, x_i2, …, x_ik, …, x_in    k = 1, …, n

这时的平均值为:x_i =(1/n)∑x_ik

按贝塞尔法计算单次测量的标准差:

而平均值的标准差即标准误为s(x_i)=σ(x_i)/

在不确定度计算中, X_i的平均值x_i就是X_i的最佳值, 而平均值的标准差就是标准不确定度的A类评定:

由于其中唯一的限制条件为∑(x_ik-x_i)=0, 所以u(x_i)的自由度ν_i = n -1出ν(x_i)或s(x_i)后, 也就得到了A类评定的标准不确定度u(x_i)= s(x_i); 但是, 必须注意的是在分组极差法中, 如独立测定m组, 每组n次, 则有:

在这些计算方法中用到的一些参数和自由度另有专用表值可查, 在此从略。

4.2 一个量的不等精度独立测量

对于量X_i的n次不等精度独立测量, 得到的系列数值为:x_i1, x_i2, …, x_in, 每次测量的权重为:p_i1, p_i2, …, p_in, 则有:

当用最小二乘法求得X_i的最佳值x_i时, 也有相应公式计算s(x_i)和ν_i。

5 标准不确定度的B类评定 5.1

已知X_i的展伸不确定度U(x_i)及其对应的包含因子k_i, 则:

标准不确定度的B类评定为:u(x_i) =U(x_i)/ k_i,

通常从制造说明书、标准、证书、手册等资料来源, 可以知道X_i的不确定度U(x_i)对其标准差的倍数为k_i, 这个k_i就是包含因子, 所以标准不确定度u(x_i)就可以简单取为U(x_i)/ k_i。

5.2

已知X_i估计值x_i的变化半范围为a, 则B类标准不确定度的评定结果为:u(x_i)= a/k_i, 其自由度为:ν_i =(1/2)[σ(u)/u]^-2, 其中σ(u)/u为估计u的相对标准差。当X_i服从正态分布时, 根据a对应的置信水平p依次取k_i如下:

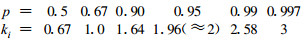
当X_i服从均匀分布时, 取

6 不确定度的合成

设被测量Y取决于各个测量值X_i, 其对应的标准不确定度分量为:

则合成标准不确定度为:

当各分量完全不相关, 即相关系数r = 0时, 用平方和法合成:

当各分量完全正相关, 即相关系数r = 1时, 用线性和法合成:

7 展伸不确定度的计算

根据定义, 展伸不确定度U = ku_c, u_c就是合成标准不确定度u_c(y), 其中的包含因子k可以利用t分布计算:k = t_p(ν), 这里的p为置信水平, 对于一般要求p = 0.95, 对于高要求p = 0.99。

ν_c为被测量Y的合成自由度, 它与各分量的自由度ν_i的关系为:

如前所述, 对于A类评定, ν_i=n-1,

对于B类评定, ν_i=(1/2)[σ(u)/ u] ^-2

当n >30时, k值或t_p(ν)值比较稳定, 与ν无关, 可取k =2(一般要求)或k=3(高要求); 由于缺少ν_i值, 无法计算ν时, 也可取k =2 ~ 3。

8 不确定度的报告 8.1

有自由度ν时:

测量结果的展伸不确定度   U = … (U由合成标准不确定度u_c = …, 及基于自由度ν=…, 置信水平p=…的t分布临界值所得包含因子k = …而得)。

8.2

无自由度ν时:

测量结果的展伸不确定度   U = … (U由合成标准不确定度u_c = …及包含因子k = …而得)。

8.3

展伸不确定度U及相应括号中的合成标准不确定度uc, 也可以报告其相对形式:U/|y|和u_c/|y|(当|y |≠ 0时)。

8.4

最后结论的展伸不确定度(或其相对形式)的有效数字一般为两位, (中间计算的不确定度, 可以多取一位)。

9 计算举例 9.1

用带热电偶的数字温度计, 测量某一容器内的温度, 数学模型为:

被测温度T = D +C式中:D为数字温度计的显示温度, C为热电偶修正。对该温度测量10次的结果为:

温度最佳值为:t =(1/ 10)∑t_i =400.02℃热电偶修正:c = 0.48℃

故测量结果表示为:t = t+ c = 400.02℃ + 0.48℃ = 400.5 ℃

9.2

标准不确定度的评定:

① 由上述重复测量引起的标准不确定度为A类评定标准不确定度:

② 数字温度计引起的不确定度为B类不确定。根据温度计说明书, 可知其展伸不确定度为:U(t_B) =0.6℃

由于t在(t0.6 ℃)~ (t+0.6℃)区间内都可能出现且各处出现机会一样, 而在区间外不可能出现, 故取为均匀分布, 则B类评定的标准不确定度为:u (t_B)=U(t_B)/0.35 ℃

③ 热电偶修正引起的不确定度为B类, 热电偶标准证书报告给出其展伸不确定度为:U(u)= 2.0℃, 对应的包含因子k(c)=2.58,

于是有:u(c)= U(c)/ k(c)= 2.0℃/2.58= 0.78℃

9.3 标准不确定度的合成

由:t=t+c  可知:|δ_f/δ_t|=1, |δ_f/δ_c|=1,

以上u_i互相无关, 故有:

9.4 展伸不确定度的计算

由于u₂和u₃无自由度, 所以合成标准不确定度的自由度无法计算。现取包含因子k=2, 得到展伸不确定度:

取两位有效数字U=1.7℃, 此即为总不确定度。

9.5 报告形式

测量结果的展伸不确定度U=1.7 ℃ (U为合成标准不确定度u_c=0.86 ℃及包含因子k = 2而得)。