利用模型指导药物研发与优化治疗方案是定量药理学的重要任务[1-3], 在抗肿瘤治疗领域尤其重要[4, 5]。模型的建立依赖于高质量的实验数据。异植瘤小鼠是广泛应用于抗肿瘤研究的临床前疾病动物模型[6, 7], 它能为PK/PD建模提供明确而可量化的观测指标以及连续且密集的药效学数据, 因而利用异植瘤小鼠实验数据指导抗肿瘤药的开发与治疗方案优化是非常适合PK/PD模型发挥作用的舞台[8, 9]。抗肿瘤药PK/PD模型以药物在免疫缺陷小鼠中的药时曲线以及异植瘤小鼠长期给药后的肿瘤生长曲线为建模数据集, 基于假定模型结构, 利用非线性混合效应模型法逐步拟合模型参数, 用以描述给药后“剂量-血药浓度-生物标志物(biomarker, BM)水平-肿瘤体积”的经时过程[10]。应用PK/PD模型可基于模拟以优化剂量与给药方案[11, 12], 评价联用方案的协同效能[13, 14], 搜寻优效的联用剂量组合[11], 初步预测药物在人体的有效剂量与肿瘤抑制效能[15, 16], 定量地阐释药物作用于靶点后BM浓度变化所驱动的肿瘤增长抑制机制[12, 17]。
本文系统地回顾了抗肿瘤药PK/PD模型的发展历史, 介绍了主流模型的诞生背景、适用范围与应用局限, 详细综述了创新抗肿瘤药PK/PD模型的研究进展, 最后从作用机制探索、联合用药优化以及临床转化预测方面列举了PK/PD模型在抗肿瘤药物研究中的应用实践。
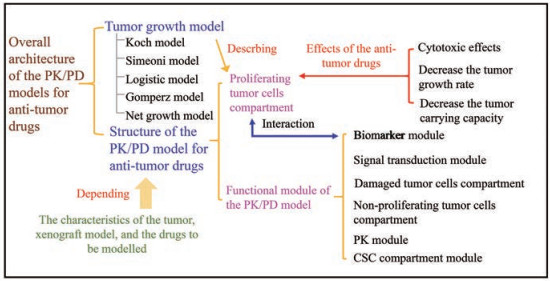
1 抗肿瘤药PK/PD模型:历史回顾本文将抗肿瘤药PK/PD模型归纳为两部分(图 1):一是肿瘤增殖模型, 是对肿瘤增殖隔室的增殖速率及其如何被药物干预的数学描述; 二是模型构架, 是增殖隔室与其他模型元件组合后构成的整体模型框架, 反映肿瘤自身及药物的药理特点。在回顾抗肿瘤药PK/PD模型结构历史演变时, 本文将穿插介绍肿瘤增殖模型。
|
Figure 1 Schematic representation of the overall model architecture for the modeling of anti-tumor agents |
早期的抗肿瘤药PK/PD模型将肿瘤视为均匀整体, 模型仅含单一增殖隔室[18] (图 2A), 药物对肿瘤的杀伤作用通过在肿瘤增殖模型中引入负数项实现, 其微分方程如式1所示:

|
Figure 2 Schematic representation of the model structure evolution in the PK/PD modeling of anti-tumor drugs |
| $ \frac{{{\rm{d}}N}}{{{\rm{d}}t}} = {\rm{growth}}\left( N \right) - k \cdot C \cdot N $ | (1) |
N代表肿瘤体积, growth (N)是肿瘤增殖模型, 即描述增殖隔室增殖速率的函数, 它在单增殖隔室模型中是肿瘤体积N的函数, 而在非单增殖隔室模型(即增殖隔室与其他模型元件链接所构成的模型)中是增殖隔室细胞体积X1、肿瘤总体积N的函数, 表达为growth (N, X1)。k代表药物的自然杀伤系数, 药物对肿瘤的杀伤作用往往与药物浓度呈线性[19, 20]或Hill方程[11]关系。模型发展早期的肿瘤增殖模型基于人口增长模型发展而来, 包括净增长模型[18]、Logistic[21]、Gompertz[22]等模型(表 1[13, 18, 20-23])。净增长模型适合描述指数生长曲线, 而Logistic和Gompertz模型适合描述S形生长曲线——肿瘤生长后期, 由于营养缺乏与肿瘤自限, 其生长趋于静息或停滞, 生长曲线出现明显平台期。肿瘤载荷(KP或Nss)是Logistic与Gompertz模型中的重要参数, 定义为最大可维持的肿瘤体积[13], 它与肿瘤的血供与营养有关。
| Table 1 Summary of the tumor growth model |
除细胞毒性作用外, 药物还可通过降低肿瘤增殖速率(式2, 例如地塞米松[16, 24-27])或降低肿瘤载荷(式3, 例如VEGFR抑制剂卡博替尼[13])的方式干预肿瘤, 表 2对这些干预方式的数学表达进行了系统总结。药物对增殖隔室干预的数学表达具有普适性, 其亦能描述增殖隔室与其他元件链接后构成的复杂模型。从现代PK/PD建模角度看, 肿瘤在未受药物干预时常被视为由单一增殖隔室组成, 用以拟合肿瘤自然生长相关参数[11]。
| 表 2 Mathematical expressions describing the tumor growth inhibition effects driven by the drug concentration in plasma or the change in biomarker level |
| $ \frac{{{\rm{d}}\mathit{N}}}{{{\rm{d}}t}} = \left( {1 - k \cdot C} \right) \cdot {\rm{growth}}\left( N \right) $ | (2) |
| $ \frac{{{\rm{d}}{X_1}}}{{{\rm{d}}t}} = {k_{{\rm{ng}}}} \cdot {X_1} \cdot \left( {1 - \frac{{{X_1}}}{{KP \cdot \left( {1 - k \cdot C} \right)}}} \right) $ | (3) |
肿瘤具有高度的异质性, 根据增殖状态可划分为处于细胞周期中的增殖期细胞与处于G0期的非增殖期细胞, 增殖期细胞对周期特异性药物敏感, 而非增殖期细胞不敏感[18]。非增殖期细胞静息一段时间后可转变为增殖期细胞, 这往往与肿瘤的复发有关。针对上述特点, Jusko[28]在1973年提出了周期特异性模型(图 2B), 该模型在单增殖隔室的基础上引入了一个可相互转化的非增殖隔室, 假定肿瘤体积为两隔室的细胞体积之和, 药物对肿瘤的干预仅发生于增殖隔室, 但增殖隔室的增殖速率亦与肿瘤总体积有关[18]。当增殖期细胞被杀灭后, 部分非增殖期细胞将转化为增殖期细胞致使肿瘤重新生长, 因而持续的药物暴露才能产生长效的肿瘤抑制。值得强调的是, 这个古老的模型奠定了具有周期特异性特点的药物的建模基础, 现今许多创新周期特异性抗肿瘤药PK/PD模型仍然未脱离该模型的基础框架[12, 29]。只有深入理解其适用范围和结构意义并结合待建模药物的药理特点才能灵活地将周期特异性模型与其他模型元件组合以搭建创新PK/PD模型。
1.3 细胞分布延时模型与信号分布延时模型药效相对药物暴露延迟是抗肿瘤治疗最重要的特点之一。为描述这种延迟, 具有一定相似性但机制完全不同的两种模型相继被提出, 即Lobo与Balthasar[18]在2002年提出的信号分布延时模型(signal distribution model, SDM, 图 2D)与Simeoni等[20]在2004年提出的细胞分布延时模型(cell distribution model, CDM, 图 2C)。二者均利用传导隔室模块(transit compartment model)[30]辅助描述药效的延时过程, 不同之处在于信号分布延时模型描述了从药物暴露到自然杀伤信号传递至肿瘤细胞的延时过程, 而细胞分布延时模型描述了肿瘤细胞从被杀伤到完全凋亡而不再占据肿瘤体积的延时过程。Yang等[31]从应用性与相互可替换性方面对比了这两种延时模型, 研究表明, 虽然二者都能较好地描述药效延迟, 但它们所描述的机制具有本质不同, 难以相互替代。信号分布延时模型在描述药效延迟上更具灵活性且对稀疏数据的拟合更具稳健性[31]。纵观近十五年的文献报道, 细胞分布延时模型已成为近年来抗肿瘤药PK/PD模型的主流构架[11, 13-15, 26, 29, 32-35], 这可能因为其模型参数更易从生理/药理层面阐释药物效能与作用特点。另一方面, 级联凋亡隔室真实地反映了肿瘤细胞受损后逐步凋亡的过程。
细胞分布延时模型可用式4~8所示微分方程组描述(图 2C):
| $ \frac{{{\rm{d}}{X_1}}}{{{\rm{d}}t}} = {\rm{growth}}\left( {X, N} \right) - {k_2} \cdot C \cdot {X_1}\;\;\;\;\;\;{X_1}\left( 0 \right) = {V_0} $ | (4) |
| $ \frac{{{\rm{d}}{X_2}}}{{{\rm{d}}t}} = {k_2} \cdot C \cdot {X_1} - {k_1} \cdot {X_2}\;\;\;\;\;\;{X_2}\left( 0 \right) = 0 $ | (5) |
| $ \frac{{{\rm{d}}{X_3}}}{{{\rm{d}}t}} = {k_1} \cdot \left( {{X_2} - {X_3}} \right)\;\;\;\;\;{X_3}\left( 0 \right) = 0 $ | (6) |
| $ \frac{{{\rm{d}}{X_4}}}{{{\rm{d}}t}} = {k_1} \cdot \left( {{X_3} - {X_4}} \right)\;\;\;\;\;{X_4}\left( 0 \right) = 0 $ | (7) |
| $ N = {X_1} + {X_2} + {X_3} + {X_4} $ | (8) |
上述微分方程组中, X1代表增殖隔室; X2-4代表级联凋亡隔室, 即不同凋亡状态的受损肿瘤细胞; N代表肿瘤总体积, 即增殖隔室与凋亡隔室中细胞体积之和。药物暴露使肿瘤细胞由增殖隔室向凋亡隔室转移。凋亡隔室由若干传导隔室组成, 隔室数目依据模型拟合情况而定[26], 文献经验值为3个[23, 36, 37], 可很好地描述多数情况的药效滞后。k2代表药物的自然杀伤系数, 反映药物对肿瘤的瞬时杀伤能力, 这种杀伤能力与药物浓度呈线性或Hill方程相关[14, 38]; k1代表受损肿瘤细胞在级联凋亡隔室中的传递速率, 即受损后的肿瘤细胞逐步凋亡的速度, 这种速度取决于肿瘤细胞自身特点及药物对肿瘤的损伤类型, 反映药物对肿瘤的持久杀伤能力[38]。由于细胞分布延时模型假定药物不会对已受到药物损伤的肿瘤细胞再产生杀伤作用, 这种持久杀伤能力与药物浓度无关[14, 38]。
Simeoni等[20]在其细胞分布延时模型的报道中提出了新的肿瘤增殖模型—Simeoni肿瘤增殖模型(表 1), 假定肿瘤生长可划分为早期的指数相与晚期的线性相, 当肿瘤体积到达阈值(Nth = λ0/λ1, λ0与λ1分别表示指数与线性生长速率常数)后立即由指数增长转变为线性增长, 在经验因子Ψ较大时(Ψ= 20), 可用式9 (上部为单增殖隔室形式, 下部为非单增殖隔室形式)表达两相增长过程。Koch等[23]在2009年对Simeoni肿瘤增殖模型作了进一步改进以描述肿瘤平缓地从指数相向线性相过渡的过程(式10, 即Koch肿瘤增殖模型, 见表 1)。至此, 共有5种肿瘤增殖模型可描述肿瘤生长曲线: Simeoni和Koch双相模型具有广泛的适用性, 是现今最常见的模型; Gompertz和Logistic等自限模型则被应用于抗血管生成药物的PK/PD建模[13, 34]。近来在沃利替尼的PK/PD建模中, 研究者尝试将两相模型与自限模型组合(式11), 利用Simeoni模型描述初期的两相生长, 利用Logistic模型的自限部分描述后期的生长停滞[15], 这种组合方式进一步增强了肿瘤增殖模型的灵活性。
| $ \begin{array}{l} \frac{{{\rm{d}}N}}{{{\rm{d}}t}} = \frac{{{\lambda _0}N}}{{{{\left[ {1 + {{\left( {\frac{{{\lambda _0}}}{{{\lambda _1}}} \cdot N} \right)}^\psi }} \right]}^{\frac{1}{\psi }}}}}\\ \frac{{{\rm{d}}{X_1}}}{{{\rm{d}}t}} = \frac{{{\lambda _0}{X_1}}}{{{{\left[ {1 + {{\left( {\frac{{{\lambda _0}}}{{{\lambda _1}}} \cdot N} \right)}^\psi }} \right]}^{\frac{1}{\psi }}}}} - {k_2} \cdot C \cdot {X_1} \end{array} $ | (9) |
| $ \begin{array}{l} \frac{{{\rm{d}}N}}{{{\rm{d}}t}} = \frac{{2{\lambda _0}{\lambda _1} \cdot N}}{{{\lambda _1} + 2{\lambda _0} \cdot N}}\\ \frac{{{\rm{d}}{X_1}}}{{{\rm{d}}t}} = \frac{{2{\lambda _0}{\lambda _1} \cdot {X_1}^2}}{{\left( {{\lambda _1} + 2{\lambda _0}{\lambda _1}{X_1}} \right) \cdot N}} - {k_2} \cdot C \cdot {X_1} \end{array} $ | (10) |
| $ \frac{{{\rm{d}}{X_1}}}{{{\rm{d}}t}} = \frac{{{\lambda _0} \cdot {X_1}}}{{{{\left[ {\left( {1 + {{\left( {\frac{{{\lambda _0}}}{{{\lambda _1}}} \cdot N} \right)}^\psi }} \right)} \right]}^{\frac{1}{\psi }}}}} \cdot \left( {1 - \frac{N}{{{N_{{\rm{ss}}}}}}} \right) $ | (11) |
多药联合是抗肿瘤治疗的常见策略。Koch等[23]于2009年在细胞分布延时模型的基础上建立了联合用药的PK/PD模型(图 3A), 引入基于经验的协同指数φ来表征协同作用。以两种细胞毒性药物联用为例, 式12是联用模型中增殖隔室的微分方程, k2, a与k2, b是两药单药建模所获得的自然杀伤系数, 协同指数φ与联合治疗对肿瘤的持久杀伤能力k1通过固定住单药的PD参数后对联合用药数据进行拟合得到, 因此, 可视φ为联合用药使某药PD参数增大的倍数—φ < 1时表示有拮抗作用; φ= 1时表示有加和作用; 而φ > 1时表示有协同作用[23]。通过对比联合治疗与单药治疗时药物的瞬时(用协同指数φ表征)与持久杀伤能力(用受损肿瘤细胞在凋亡隔室的传递速率k1表征, 图 3A)变化, 联用模型还可帮助研究者去定性地探索协同机制。Li等[14, 38]在对厄洛替尼与吉西他滨在H1299异植瘤小鼠中联用进行PK/PD建模研究时发现吉西他滨可使增殖隔室的细胞迅速停止增殖, 但药效几乎无滞后, 厄洛替尼药效滞后明显, 但瞬时杀伤作用较小。二者同时给药方案中, 两药的瞬时杀伤作用表现为加和作用(φ= 0.961)且药效滞后较单独治疗更短; 二者间隔给药方案(即先给予厄洛替尼, 18 h后再给予吉西他滨)中, 两药的瞬时杀伤作用表现为协同作用(φ= 1.82), 且药效滞后时间比吉西他滨单用长, 因而间隔给药方案展现出更优异的临床转化潜力。
| $ \frac{{{\rm{d}}{X_1}}}{{{\rm{d}}t}} = {\rm{growth}}\left( {X, N} \right) - \left( {{k_{{\rm{2, a}}}}{C_1} + \varphi \cdot {k_{{\rm{2, b}}}}{C_2}} \right) \cdot {X_1} $ | (12) |

|
Figure 3 Schematic representation of recent advances in the PK/PD modeling of combination therapies of cancer |
作为一种经验性方法, Koch联用模型能有效地描述联合用药时的肿瘤生长曲线并外推预测协同机制相似的给药方案或剂量组合的肿瘤增长抑制曲线[11, 26], 广泛应用于评价不同给药方案的协同效能[13, 14]。但其亦有经验模型的共有局限性:其一, 它只能描述药物的协同现象, 但模型结构中却不含协同机制, 无法帮助研究者去定量地探索协同机制。其二, 化疗药与分子靶向药联用的协同效果往往十分依赖于给药方案[13, 14, 39-41] (例如同时给药、间隔给药、序贯给药), 不同方案的协同机制往往有本质的不同, Koch联用模型更适合预测建模数据集的联用方案以不同剂量组合时的效能(因为它们具有类似的协同机制), 但难以外推建模数据集以外联用方案的肿瘤抑制情况。
1.5 经典PK-BM-PD模型分子靶向抗肿瘤药的效应物质基础是其所靶向的BM的浓度变化, 纳入BM因素的PK/PD模型有助于定量揭示BM变化与肿瘤生长/抑制的内在联系。在经典BM模型中, 间接效应模型[42] (indirect effect model, IDR)与链接模型[43] (link model)是描述内源性物质经时过程的常用方法。图 2E以厄洛替尼为例展示了经典的PK-BM-PD模型构架[33], 该模型假定药物通过抑制生成或促进降解的方式干预BM, 当BM低于维持肿瘤细胞正常功能所需浓度水平时(即偏离基线)造成细胞毒性作用。为了从数学上描述BM越低而细胞毒性作用越强的现象, BM浓度被折算为浓度降低百分比I%, 假定细胞毒性效能与I%以线性或Hill方程关系相链接(表 2)。经典PK-BM-PD模型有其内在局限性。首先, 肿瘤与其对应的BM并非两个孤立系统, 激酶浓度异常往往与致癌突变有关, 而肿瘤的恶劣程度亦可能影响BM浓度, 而在经典PK-BM-PD模型架构中, 肿瘤增殖模块无法对BM模块产生影响。其次, 经典PK-BM-PD模型以初始状态BM浓度作为基线, 但基线水平的定义亦可能随肿瘤的发展而变化, 即不同状态的肿瘤细胞维持正常功能所需的BM浓度水平可能不同, 在未来可能需纳入疾病进展模型等元件来校准基线[17]。最后, 经典PK-BM-PD模型中用于描述BM水平变化的IDR模型结构简单, 纳入的BM效应指标数量少, 难以定量地阐释药物作用于靶点后逐级影响下游信号并干预肿瘤发展的过程。
2 抗肿瘤药PK/PD模型:研究进展经典的抗肿瘤药PK/PD模型可较好地描述多数药物在异植瘤小鼠中的肿瘤抑制效能, 但随着人类对肿瘤认识的深入, 新的抗肿瘤靶点与机制不断涌现, 研究目的也更加多元化。定量药理学的发展要求PK/PD模型不仅要描述肿瘤生长曲线, 还要提供更多的内在性机制性信息。这些“看不见的信息” (例如BM与肿瘤的交互作用[17, 44]、肿瘤细胞的周期动力学[12]或细胞异质性变化[34]、药效信号传导速度[45])有助于揭示药物剂量依赖性的药理学行为, 药效延迟的限速步骤, 提示肿瘤的预后与复发, 以及优化创新药物给药方案。要实现上述需求, 就需要在结构上具有创新性的抗肿瘤药PK/PD模型。
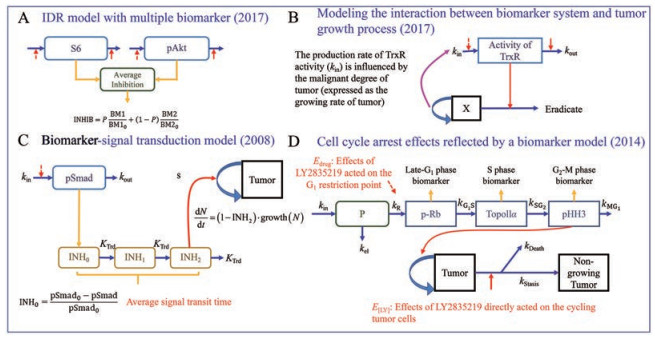
2.1 创新靶点药物的PK/PD建模研究进展 2.1.1 细胞周期动力学模型细胞周期蛋白依赖性激酶4/6 (cyclin dependent kinase 4/6, CDK4/6)是控制细胞通过G1期检查点的关键调节因子, 抑制CDK4/6可使细胞静息于G1期而抑制肿瘤增殖。LY2835219是一个处于临床开发中的新型CDK-4/6抑制剂, Tate等[12]建立了一个以BM模型表征细胞周期动力学过程的半机制性PK/PD模型以定量阐释LY2835219对细胞周期的调控作用及其随后对肿瘤增殖的抑制过程。图 4D展示了该模型的框图, 式13~15为其微分方程组, p-Rb、TopoⅡα、pHH3是特定细胞周期的代表性标志物, 模型的PD观测指标之一, 应用这些标志物可表征细胞周期密度的相对变化。BM模型是由P、p-Rb、TopoⅡα、pHH3等四个隔室组成的开环细胞周期级联传导隔室, 代表了细胞周期的传递。四个隔室分别代表早G1期(G1检查点前G1期细胞)、晚G1期(G1检查点后G1期细胞)、S期与G2-M期肿瘤细胞, kR是肿瘤细胞通过G1期检查点(即由早G1期转向晚G1期)的速率常数。模型假定肿瘤由增殖期细胞与非增殖期细胞组成, 药物按比例降低kR而使肿瘤静息于G1期。当细胞周期被持久静息时, G2M期细胞密度亦随之降低, 而增殖期细胞的增殖速率与G2M期细胞密度(即pHH3的相对变化程度, 式13)成正比, 肿瘤增殖由此被抑制。药物在高剂量下还可以一种浓度依赖性的方式直接作用于增殖期肿瘤期细胞, 促进其增殖静息而转向非增殖细胞与凋亡(式13~15, 图 4D, E[LY]为药物对增殖期细胞的直接效应而Edrug为药物对细胞周期的静息效应)。该模型不仅可在后续研究中为CDK4/6抑制剂的开发提供定量药理学信息, 还为以细胞周期为靶点的药物的PK/PD建模提供了宝贵思路。
|
Figure 4 Schematic representation of recent advances in the PK-BM-PD modeling of anti-tumor drugs |
| $ \begin{array}{l} \frac{{{\rm{d}}{T_{\rm{g}}}}}{{{\rm{d}}t}} = {E_{{\rm{pHH3}}}} \cdot \frac{{{\lambda _0} \cdot {T_{\rm{g}}}}}{{{{\left[ {\left( {1 + {{\left( {\frac{{{\lambda _0}}}{{{\lambda _1}}} \cdot {T_{\rm{g}}}} \right)}^\psi }} \right)} \right]}^{\frac{1}{\psi }}}}} - \\ \;\;\;\;\;\;\;\;\;{E_{\left[ {{\rm{LY}}} \right]}} \cdot \left( {{k_{{\rm{stasis}}}} + {k_{{\rm{death}}}}} \right) \cdot {T_{\rm{g}}} \end{array} $ | (13) |
| $ \frac{{{\rm{d}}{T_{{\rm{ng}}}}}}{{{\rm{d}}t}} = {E_{\left[ {{\rm{LY}}} \right]}} \cdot {k_{{\rm{stasis}}}} \cdot {T_{\rm{g}}} $ | (14) |
| $ \begin{array}{l} {E_{{\rm{pHH3}}}} = \frac{{{\rm{pHH}}{{\rm{3}}^{{\gamma _1}}}}}{{{\rm{pHH3}}_0^{{\gamma _1}}}}\;\;\;\;\;\;{E_{\left[ {{\rm{LY}}} \right]}} = \frac{{C_{{\rm{Cen}}}^{{\gamma _2}}}}{{C_{50}^{{\gamma _2}} + C_{{\rm{Cen}}}^{{\gamma _2}}}}\\ {E_{{\rm{Drug}}}} = \frac{{{I_{\max }} \cdot {C_{{\rm{cen}}}}}}{{{\rm{I}}{{\rm{C}}_{50}} + {C_{{\rm{cen}}}}}} \end{array} $ | (15) |
Yates等[29]结合Simeoni模型、细胞分布延时模型、周期特异性模型以及肿瘤的真实增殖分化机制, 建立了一个新型周期特异性模型(图 2F, 式16和17)。模型以肿瘤细胞在增殖状态(cycling state)与非增殖状态(non-cycling state)的循环表征细胞周期变化, 假定增殖状态细胞以有丝分裂的方式进入非增殖状态—每当一倍体积的细胞离开增殖状态, 两倍体积的细胞将进入非增殖状态。有丝分裂的一级速率常数为Simeoni肿瘤增殖模型的指数相增长速率λ0; 一部分非增殖状态细胞可继续维持分裂而转向增殖状态(式17), 非增殖状态细胞向增殖状态细胞的转化随着肿瘤体积的增加而愈发受限(式19), 使肿瘤在后期转向线性增长。AZD8055可通过降低速率常数的方式抑制有丝分裂, 抑制程度与AZD8055对其所靶向的BM的平均抑制程度INHIB相关(式24, 图 2F-b)。有丝分裂被抑制使肿瘤细胞静息于增殖状态, 为体现细胞静息所造成的细胞毒性效果, 模型假定细胞在增殖状态停留时间延长时将逐渐凋亡, 凋亡速率与其在增殖状态的平均滞留时间(mean residence time, MRT, 式18表示平均滞留时间随有丝分裂受抑制而延长, 图 2F-a)呈现Hill方程关系, 受损细胞通过级联凋亡隔室而被完全消除。该模型在结构上体现了肿瘤细胞在增殖状态与非增殖状态的交替、细胞有丝分裂、药物作用周期特异性、细胞静息造成毒性作用以及受损细胞级联凋亡等多个过程, 这使得模型框架容易纳入其他药物机制, 是近年来周期特异性模型在结构上的最大更新。
| $ \begin{array}{l} \frac{{{\rm{dCycling}}}}{{{\rm{d}}t}} = \frac{{{\lambda _0}{\rm{NonCycling}}}}{{{{\left[ {1 + {{\left( {\frac{{{\lambda _0}}}{{{\lambda _1}}}{\rm{NonCycling}}} \right)}^\phi }} \right]}^{\frac{1}{\phi }}}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Cycling}} \cdot {\lambda _0} \cdot {\rm{INHIB}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Cycling}}\frac{{{E_{\max }} \cdot {\rm{MR}}{{\rm{T}}^N}}}{{{\rm{MR}}{{\rm{T}}^N} + {\rm{MRT}}_{50}^N}} \end{array} $ | (16) |
| $ \begin{array}{l} \frac{{{\rm{dNonCycling}}}}{{{\rm{d}}t}} = 2{\rm{Cycling}} \cdot \left( {{\lambda _0} \cdot {\rm{INHIB}}} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\lambda _0} \cdot {\rm{NonCycling}}}}{{{{\left[ {1 + {{\left( {\frac{{{\lambda _0}}}{{{\lambda _1}}} \cdot {\rm{NonCycling}}} \right)}^\phi }} \right]}^{\frac{1}{\phi }}}}} \end{array} $ | (17) |
| $ {\rm{MRT}} = \frac{1}{{{\lambda _0} \cdot {\rm{INHIB}}}} $ | (18) |
| $ {\rm{Rat}}{{\rm{e}}_{{\rm{noncycling}} \to {\rm{cycling}}}} = \frac{{{\lambda _0} \cdot {\rm{NonCycling}}}}{{{{\left[ {1 + {{\left( {\frac{{{\lambda _0}}}{{{\lambda _1}}} \cdot {\rm{NonCycling}}} \right)}^\phi }} \right]}^{\frac{1}{\phi }}}}} $ | (19) |
肿瘤干细胞(cancer stem-like cell, CSC)的自我更新与分化导致了肿瘤的细胞异质性[46], 传统抗肿瘤药仅能作用于分化的正常肿瘤细胞(differentiated tumor cells, DTC)而很难对CSC产生有效的杀伤或抑制[47]。尽管在治疗初期肿瘤体积表现为减小, 但一段时间后CSC又可分化出耐药细胞而导致肿瘤复发[47]。多巴胺受体(具有5个亚型D1DR~D5DR)是可用于靶向CSC的靶点, 其特异性地表达于CSC表面[48]。研究表明, 激活D1DR或拮抗D2DR均有助于抑制CSC[25, 49]。近年来, 有报道[25, 34, 50, 51]围绕以多巴胺受体为靶点的CSC靶向治疗联合抗肿瘤治疗建立了一系列PK/PD模型。研究者将CSC靶向治疗视为抗肿瘤治疗的增敏剂, 假定其无法直接抑制肿瘤, 但可改变共服抗肿瘤药的PD参数而增强其抗肿瘤活性(图 3B和3C)。例如D2DR受体拮抗剂舒必利可以Hill方程关系降低地塞米松对肿瘤增殖抑制PD参数的EC50值, 使地塞米松的PD特征表现为对肿瘤更敏感[25] (图 3B)。多巴胺可激动D1DR受体而抑制CSC, 多巴胺与舒尼替尼或阿昔替尼联用在A549与MCF-7/Adr异植瘤小鼠中均展现出良好的协同效能且能降低联合治疗组的CSC频率[34, 49-51] (即CSC在肿瘤细胞中的占比, 反映肿瘤的异质性)。多巴胺因半衰期极短而难以获得PK参数, 因此无法将多巴胺以血药浓度的形式纳入模型。幸运的是, 研究表明多巴胺对CSC的抑制不呈剂量依赖性且效应约可持续3天[34, 51], 呈现为“全或无”特点。这种情况下, 研究者将多巴胺存在与否作为0、1二值协变量纳入模型, 是否与多巴胺联用作为固定效应改变了抗肿瘤药的PD参数而在模型中体现出协同作用[50, 51] (图 3C)。上述两种建模方式提供了不同于“协同指数”的建模思路, 对未来的联合用药建模有启发意义。
尽管上述建模案例确实在参数层面上展现了CSC靶向治疗对于抗肿瘤治疗的增敏作用, 但仍未在模型结构中体现出二者依赖于CSC的相互作用过程。再者, 经典PK/PD模型仅预测肿瘤体积, 尚不足以体现治疗过程中的肿瘤细胞异质性变化, 而异质性变化对描述肿瘤的耐药、复发与预后有启发意义。针对上述不足, Wang等[34]在细胞分布延时模型基础上纳入CSC隔室, 建立了一个完全基于机制的舒尼替尼与多巴胺的联合治疗PK/PD模型(图 2G, 式20和21)。模型以肿瘤体积与CSC频率作为PD观测指标, 假定CSC与DTC均可增殖且能相互转化, CSC与增殖的分化肿瘤细胞(proliferating differentiated tumor cells, pDTC)的增殖过程分别用Logistic与Koch模型描述, pDTC的去分化过程以一阶动力学过程kdc表示, CSC的分化过程以带反馈的零阶动力学Rcd表示。模型中, 舒尼替尼通过促进DTC凋亡的方式展现其抗肿瘤活性, 使pDTC进入级联凋亡隔室转为非增殖的DTC (non-proliferating differentiated tumor cells, npDTC)而逐渐凋亡(式21, 图 2G-d); 但舒尼替尼的抗血管生成作用所形成的局部缺氧环境亦可加快CSC增殖[52-54] (式20, 图 2G-a), 使CSC频率升高, 对舒尼替尼敏感的肿瘤细胞相对减少, 造成舒尼替尼抗肿瘤效能降低与耐药。多巴胺可靶向CSC以减小CSC的载荷(式20, 图 2G-b)及促进CSC分化(图 2G-c), 从而降低CSC频率, 使更多的肿瘤细胞能被舒尼替尼杀伤。与上文案例相似, 多巴胺给药与否仍作为协变量被纳入模型(式20和21)。该模型成功地将肿瘤负荷与肿瘤细胞异质性链接在一起, 有助于研究者深入理解CSC靶向治疗与抗肿瘤治疗联合的协同机制、协同效能、预后情况与耐药可能性, 该模型亦为机制性联合用药PK/PD建模提供了可供参考的代表案例。
| $ \begin{array}{l} \frac{{{\rm{dCSC}}}}{{{\rm{d}}t}} = {k_{\rm{g}}} \cdot \left( {1 + \frac{{{E_{{\rm{max, sun}}}} \cdot {C_{{\rm{sun}}}}}}{{{C_{{\rm{50, sun}}}} + {C_{{\rm{sun}}}}}}} \right) \cdot {\rm{CSC}} \cdot \\ \left( {1 - \frac{{{\rm{CSC}}}}{{{\rm{CS}}{{\rm{C}}_{{\rm{ss}}}} \cdot {\rm{Inh}}_{{\rm{DA}}}^{{\rm{DOPA}}}}}} \right) + {k_{{\rm{dc}}}} \cdot {\rm{DTC}} - {R_{{\rm{cd}}}} \cdot \\ \left( {1 + {\rm{Ef}}{{\rm{f}}_{{\rm{DA}}}} \cdot {\rm{DOPA}}} \right) \cdot {\left( {\frac{{{\rm{CSC}} \cdot {\rm{DT}}{{\rm{C}}_0}}}{{{\rm{DTC}} \cdot {\rm{CS}}{{\rm{C}}_0}}}} \right)^\gamma } \end{array} $ | (20) |
| $ \begin{array}{l} \frac{{{\rm{d}}p{\rm{DTC}}}}{{{\rm{d}}t}} = \frac{{2{\lambda _0}{\lambda _1} \cdot p{\rm{DTC}}}}{{{\lambda _1} + 2{\lambda _0} \cdot p{\rm{DTC}}}} \cdot \frac{{p{\rm{DTC}}}}{{{\rm{DTC}}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{k_{{\rm{dc}}}} \cdot p{\rm{DTC}} - {k_{{\rm{ap}}}} \cdot {C_{{\rm{sun}}}} \cdot p{\rm{DTC}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{R_{{\rm{cd}}}} \cdot \left( {1 + {\rm{Ef}}{{\rm{f}}_{{\rm{DA}}}} \cdot {\rm{DOPA}}} \right) \cdot {\left( {\frac{{{\rm{CSC}} \cdot {\rm{DT}}{{\rm{C}}_0}}}{{{\rm{DTC}} \cdot {\rm{CS}}{{\rm{C}}_0}}}} \right)^\gamma } \end{array} $ | (21) |
与肿瘤发生发展有关的BM浓度异常往往促进肿瘤增殖, 而肿瘤恶化又可能反过来促进这些BM合成, 形成一个正反馈循环。乙烷硒啉是一种以硫氧还蛋白还原酶(thioredoxin reductase, TrxR)为靶点的新型抗肿瘤药[55]。临床证据显示, 患者肿瘤中TrxR活性水平随肿瘤恶性程度增加而显著升高[44], 准确地捕捉该特性有助于揭示TrxR活性变化与肿瘤增殖的内在联系。Ye等[17]建立了一个纳入BM与肿瘤增殖交互作用的PK/PD模型(图 4B), 式22和23是描述TrxR活性和肿瘤体积关联的微分方程, 其中DOSE指日给药剂量, 作为协变量被引入模型。模型假定TrxR活性的生成速度kin与肿瘤恶性程度正相关, 而乙烷硒啉以促进TrxR失活的方式发挥其抗肿瘤活性。相比肿瘤体积, 以肿瘤增殖速率表征肿瘤恶性程度能提供更好的拟合优度且使模型更具稳健性。未给药组的TrxR活性水平被选作基线以反映肿瘤的疾病进展。乙烷硒啉使给药组的TrxR活性偏离基线, 造成细胞毒性作用而促进肿瘤细胞凋亡。该研究为肿瘤与其对应BM存在交互情景下的PK/PD建模拓宽了思路。
| $ \begin{array}{l} \frac{{{\rm{dTrxR}}}}{{{\rm{d}}t}} = {{\rm{ \mathsf{ γ} }}_1} \cdot \frac{{2{\lambda _0}{\lambda _1}N}}{{{\lambda _1} + 2{\lambda _0}N}} \cdot {k_{{\rm{in}}}} - {k_{out}} \cdot {\rm{TrxR}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 + \frac{{{S_{\max }} \cdot DOS{E^{{\gamma_2}}}}}{{SC_{50}^{{\gamma_2}} + DOS{E^{{\gamma_2}}}}}} \right) \end{array} $ | (22) |
| $ \begin{array}{l} {\rm{TrxR}}\left( 0 \right) = \frac{{{k_{{\rm{in}}}}}}{{{k_{{\rm{out}}}}}}\\ \frac{{{\rm{d}}N}}{{{\rm{d}}t}} = \frac{{2{\lambda _0}{\lambda _1}N}}{{{\lambda _1} + 2{\lambda _0}N}} - \frac{{{E_{\max }} \cdot E}}{\begin{array}{l} E{C_{50}} + E\\ \end{array}}\\ N\left( 0 \right) = {N_0}\;\;\;\;\;\;\;E = 1 - \frac{{{\rm{Trx}}{{\rm{R}}_{{\rm{Treatment}}}}}}{{{\rm{Trx}}{{\rm{R}}_{{\rm{Control}}}}}} \end{array} $ | (23) |
mTOR激酶抑制剂AZD8055作用于靶点后可影响下游pS6与pAKT浓度, Yates等[29]应用式24折算药物对全部BM的平均抑制程度(图 4A), 其中P的拟合有助于评估药物对每种BM的干预作用对最终抗肿瘤响应的相对贡献程度。
| $ {\rm{INHIB}} = P \cdot \frac{{{\rm{AKT}}}}{{{\rm{AT}}{{\rm{K}}_0}}} + \left( {1 - P} \right) \cdot \frac{{S6}}{{S{6_0}}} $ | (24) |
经典PK-BM-PD模型假定BM浓度变化会立即干预肿瘤[33, 56, 57]。然而, 一些BM以启动下游信号转导的方式驱动肿瘤增殖抑制, BM-信号传导-级联模型有助于研究者深入探索药物作用于靶点后的信号传递过程。LY2157299是一个新型TGF-β激酶拮抗剂, Bueno等[45]在BM模块与肿瘤增殖模块之间添加了一个由两个隔室组成的级联信号传导模块(图 4C)组成BM-信号传导-级联模型, 可将其视为一种信号分布延时模型的延伸, 但信号的产生不由药物浓度驱动, 而由BM变化驱动。PK/PD建模结果表明, LY2157299所靶向的BM (pSmad)具有较短的周转半衰期[58] (turnover time, 18.6~32.0 min), 而信号在传导隔室的平均传递时间在6.17~28.7天, 表明信号传递延迟在LY2157299的药效延迟中占主导作用。篇幅有限, 本节仅介绍了代表性案例, 更多PK-BM-PD建模案例可参考表 3[15, 17, 21, 29, 32, 33, 45, 56, 57, 59, 60]。
| Table 3 Summary of the PK-BM-PD models published in recent years. |
双峰现象是PK建模中具有挑战性的难题, LY2835219是一个具有双峰特征的新型CDK4/6抑制剂, 第二吸收峰随剂量增加而愈加明显。Tate等[12]建立了一个经验性PK模型, 假定药物能够双路径并行吸收—可饱和的直接吸收路径1和经由传导隔室模块的间接延迟吸收路径2 (图 5A)。当给药剂量递增时, 路径1逐渐饱和而经由路径2所吸收的药物比例逐渐增加, 因而表现出剂量依赖性增强的第二吸收峰。双吸收位点是解决双峰现象的另一有效手段, 舒必利在吸收后可被P-糖蛋白外排, 而后又在胃肠道发生重吸收。为描述上述生理过程, Yao等[25]建立了一级吸收速率双吸收位点PK模型(图 5B), 并在第二吸收位点设置了吸收延迟Tlag以模拟药物被外排后的重吸收过程。

|
Figure 5 Schematic representation of the PK models for drugs and combination therapies with complicated pharmacokinetic profile |
抗肿瘤药PK/PD模型将药物的长期PK行为与其肿瘤增殖抑制链接在一起, 准确地捕捉时间依赖性PK特征将有助于提高模型对长期给药的药时曲线的预测能力。地塞米松是一个CYP3A自诱导剂, Li等[24]建立了一个纳入自诱导因素的地塞米松PK/PD模型(图 5C), 假定地塞米松系统清除率随时间呈现可饱和的Hill方程增强关系。研究者比较了纳入自诱导因素与否时模型拟合所得的肿瘤生长曲线, 发现纳入自诱导因素模型的肿瘤生长速率明显高于未纳入自诱导因素模型, 研究者推测其原因是自诱导降低了地塞米松的系统暴露与生物利用度。该案例充分表明建模时精确捕捉PK特征才能准确预测长期肿瘤生长曲线。
2.3.3 抗肿瘤联合治疗时的PK相互作用建模联合治疗中, 当共服药物存在PK相互作用(drug-drug interaction, DDI)时, 需准确区分PK环节与PD环节的DDI才能合理地估计协同指数。以卡博替尼与多西他赛为例, 二者同时给药使多西他赛的末端相半衰期产生显著变化。Chen等[13]假定卡博替尼可浓度依赖性地降低多西他赛的系统清除率, 建立了联用PK/PD模型(图 5D)。研究者对比了是否纳入DDI时最终模型的协同指数与目标函数值, 纳入DDI因素后, 最终模型的目标函数值显著降低, 表明纳入DDI提高了模型对实验数据的描述能力; 纳入DDI后所拟合出的协同指数低于未纳入时, 表明联用时一部分协同效能可能源于PK相互作用, 这在同时给药方案中尤为重要。该案例表明, 纳入DDI的PK/PD模型有助于更精确地定位不同给药方案下协同效应的作用环节, 也有助于更准确地评估协同指数大小。
3 抗肿瘤药PK/PD模型:应用实践 3.1 探索药物作用机制与优化给药方案在CDK4/6抑制剂LY2835219建模案例[12]中, 研究者通过模型模拟推断出稳态谷浓度水平不少于200 ng·mL-1时才能维持持久的细胞周期静息效果, 这从理论上支持了当前临床上CDK4/6抑制剂采用的长期给药策略。单一细胞周期静息效应难以描述LY2835219在高剂量下的药理学行为, 研究者依据药理学线索假定药物在高剂量时可以一种浓度依赖性的方式直接作用于增殖期细胞, 促进其增殖静息与凋亡(式13和式14, 图 4D), 这种假设下的模型能较好拟合25~100 mg·kg-1剂量范围长期口服给药的肿瘤生长曲线, 表明假设具有一定药理合理性。基于模拟分析, 研究者推断LY2835219在低剂量时(低于50 mg·kg-1)的抗肿瘤活性主要由细胞周期静息驱动, 而高剂量下(100 mg·kg-1)的抗肿瘤活性由增殖静息与细胞毒性驱动。长期给药方案下50 mg·kg-1时即可达到最大归因于细胞周期静息的肿瘤抑制效果, 在此暴露水平基础上进一步提高血药浓度仍可获益。LY2835219的PK/PD建模实践支持了当前CDK4/6抑制剂临床给药方案的合理性, 探索了剂量依赖性的药物作用机制与药理学行为, 并提供了可用于临床转化的最小有效LY2835219血浆浓度信息。
在多巴胺与舒尼替尼的机制性联合治疗PK/PD建模案例[34]中, 研究者模拟了同时给药(同时给予多巴胺和舒尼替尼两天, 再停止给药两天, 依次轮替)、多巴胺~舒尼替尼(先给予多巴胺两天, 再给予舒尼替尼两天, 依次轮替)、舒尼替尼~多巴胺三种给药方案的肿瘤生长曲线, 结果表明同时给药方案具有最佳肿瘤抑制率, 多巴胺~舒尼替尼与舒尼替尼~多巴胺方案的肿瘤抑制率相似, 但都不如同时给药方案。研究者后续开展的动物实验验证了模型模拟所得结论。值得一提的是, 联用PK/PD模型的建模数据集的给药方案与上述任意一种给药方案均不相同, 即该模型成功实现了跨给药方案预测肿瘤生长曲线, 验证了机制性模型强大的外推能力。该模型可提供不同给药方案下CSC频率的经时过程, 有助于研究者定量探索多巴胺与舒尼替尼在不同给药方案下的肿瘤异质性以及它们依赖于肿瘤干细胞的协同作用。
3.2 探索联合用药方案与优化联用剂量组合化疗药与分子靶向药联用的协同效能往往十分依赖给药方案[13, 14, 39-41], 准确评价不同方案的协同效能有助于优效方案的确立。不同方案的总给药量不一致, 因而无法单纯地以比较肿瘤生长曲线的方式来判断协同效能[13]。通过联合用药PK/PD建模获得协同指数φ可校正给药剂量的差异从而定量地评估协同效能[13]。Chen等[13]在对卡博替尼与多西他赛联用进行PK/PD建模研究时发现同时给药方案具有协同作用, 间隔给药方案(即两药共服, 但服药时间间隔6 h)相对同时给药方案并未提高协同效能, 而同时给药方案在临床应用上具有患者依从性高的优势[13]。多西他赛~卡博替尼序贯给药方案(即第一周给予多西他赛, 第二周给予卡博替尼, 依次轮替)具有最强协同效能, 而卡博替尼~多西他赛方案则存在拮抗作用。尽管多西他赛~卡博替尼方案因其总给药量低于同时给药方案而在肿瘤抑制率方面不如后者, 但以未来的临床转化视角看, 多西他赛~卡博替尼方案具有协同效能高、总给药剂量少的优势, 有助于降低毒性与耐药, 具有优异的转化潜力[13]。
EGFR抑制剂厄洛替尼与VEGFR抑制剂舒尼替尼联用在理论上能提高患者的获益并降低厄洛替尼诱导的耐药。然而一项Ⅲ期临床联合用药试验却提示其未能提高非小细胞肺癌患者的总体生存率[11]。Li等[11]建立了厄洛替尼与舒尼替尼联合用药的PK/PD模型, 建模结果表明厄洛替尼与舒尼替尼联用时具有良好的协同效果(φ = 4.4), 而舒尼替尼剂量对联用时的抗肿瘤效能起决定性作用, 降低厄洛替尼剂量并调整舒尼替尼剂量有助于降低毒性并提高治疗效果。进一步模拟表明, 厄洛替尼与舒尼替尼以质量比1:4联用时可取得较好的肿瘤抑制效果, 而真实Ⅲ期临床试验中二者的质量比为4:1, 这可能是Ⅲ期临床试验结果不理想的原因之一。
为定量阐释异甘草酸镁对多西他赛诱导的肝损伤的保护作用。Li等[61]建立了一个化疗药-肝保护剂联用PK-PD-TD模型(图 3D)。模型以肿瘤体积为PD指标, 以血浆谷丙转氨酶(ALTp)为毒代动力学(TD)指标, 评价不同剂量组合下的肿瘤抑制率与肝损伤作用。模型假定多西他赛能促进肝细胞中ALT释放进入血浆而异甘草酸镁可抑制这种促进释放能力, 建模结果表明, 多西他赛与异甘草酸镁在PK与PD上均无相互作用, 异甘草酸镁既不会影响多西他赛的系统暴露亦不会影响其抗肿瘤活性。进一步模拟表明, 增大异甘草酸镁剂量或提高给药频次均有助于缓解多西他赛诱导的肝损伤作用。该模型有助于研究者在后续临床转化研究中在药效与毒效之间寻找剂量平衡点, 亦为联合用药PK/PD建模提供了一个新的思路, 即不仅要关注药效上的协同作用, 亦需关注药效与毒效之间的平衡。
3.3 预测药物在人体的有效剂量与肿瘤抑制PD特征利用临床前试验数据进行建模与模拟的策略可增强研究者对药物临床转化的信心, 这是因为临床前动物模型与人类在PK和PD行为上的相似性与差异性可被定量地体现并用模型参数来表达[62]。举个例子, 假定药物在人体与异植瘤小鼠中对肿瘤具有相似的杀伤能力, 则达到肿瘤静息时需要相同的稳态靶组织游离浓度, 以该浓度为参考值并结合人体PK参数与血浆游离分数(fu, p, human)可预测人体有效剂量, 这种方法已被成功应用于厄洛替尼与吉非替尼(gefitinib)的剂量预测[63]。有报道指明, 在数个抗肿瘤药中, 临床相关暴露水平下的异植瘤小鼠肿瘤抑制率(tumor growth inhibition, TGI)与实际临床响应具有显著相关性, 若临床前疾病动物模型在临床相关剂量与给药方案下能达到60%的TGI, 则被认为可产生临床响应[64]。利用上述方法, Yao等[16]基于PANC-1与SW1990细胞系异植瘤小鼠以及胰腺癌PDX (patient-derived xenografts, 患者来源肿瘤组织异植模型)小鼠建立了地塞米松的PK/PD模型。利用地塞米松的人体PK参数(以fu, p, Human和fu, p, Mouse校正)结合其在异植瘤小鼠中的PD参数模拟预测其在人体中能达到60% TGI的剂量。模型模拟表明, 以PDX小鼠PD参数所预测的地塞米松抗胰腺癌的人体有效剂量为26 mg, 且只要每日总给药剂量一致, 给药频次对最终肿瘤抑制率影响不大, 提示临床上可采取少量多次的给药方式来降低地塞米松治疗胰腺癌时的不良反应。
沃利替尼是一个处于临床开发中的口服c-Met激酶抑制剂, Gu等[15]利用临床前试验数据建立了沃利替尼的PK/PD模型并进一步利用异速放大等经验性方法预测了沃利替尼在人体的PK参数。研究者将预测的沃利替尼人体PK参数与其在临床前模型中对c-Met抑制的PD参数结合, 初步模拟了沃利替尼在人体的暴露量及其对c-Met的抑制曲线。进一步的模拟表明, 每天给予人沃利替尼100 mg可使70%的c-Met被抑制, 这加强了研究者对沃利替尼临床转化的信心。
4 结语与展望经过数十年的发展, PK/PD模型已被广泛地应用于临床前异植瘤小鼠实验数据的探索、整合与信息挖掘, 并为治疗方案的临床转化提供理论支持。随着对定量药理学重视度的提高, 药学背景的研究人员也逐渐具备搭建具有复杂结构的模型的能力, 这将大大加快抗肿瘤药PK/PD模型的发展速度。
从结构演变趋势上看, 抗肿瘤药PK/PD模型已从一门描述性科学逐渐转变为一门机制性科学[34]。建模需要平衡模型结构复杂性与其对真实作用机制的替代性。为确保复杂模型中参数的可识别性, 需要更充足的建模数据以及更多样化的中间PD观测指标, 这使得未来的PK/PD建模对整体实验设计要求更高[34]。
从待建模药物的种类看, 小分子抗肿瘤药PK/PD模型的发展已日趋成熟, 而大分子抗肿瘤药的PK/PD建模仍在持续探索中[65]。肿瘤增殖模型仍适用于大分子抗肿瘤药[66, 67], 但大分子药物的PK/PD行为及描述它们的模型具有较高的复杂性, 靶点与药物的相互作用既产生药效又参与对药物的处置[65], 药物与靶点结合后可通过免疫毒性治疗[68]、靶细胞消除、改变细胞功能、靶向给药[66, 67] (抗体偶联药物)等方式发挥作用[65]。只有高质量的实验数据、恰当的异植瘤小鼠模型以及对大分子药物PK/PD的深入理解才能支撑模型构建。
从临床前动物模型的选择看, PDX小鼠在肿瘤微环境上与真实临床患者更具相似性[69]且保留了其异质性[70], 有理由相信PDX小鼠将提升模型的临床转化力与信服力。目前, 基于PDX小鼠的PK/PD建模案例仍较少[16, 67, 71], 但这些案例都是近两年的最新报道, 表明其可能是抗肿瘤药PK/PD模型未来的发展方向之一。Yao等[16]应用胰腺癌PDX小鼠预测了地塞米松的人体有效剂量; Singh等[67]基于肝癌PDX小鼠建立了GPC-3抗体偶联药物的生长分数-PK/PD模型以更好地预测人体有效剂量; Luo等[71]构建了POP脂质体荷载多柔比星在PDX小鼠中的光化疗(chemophototherapy, CPT) PK/PD模型, 模型参数定量地阐明光化疗增加了肿瘤血管对多柔比星的通透性以及多柔比星在肿瘤组织的蓄积。尚无文献总结经典异植瘤小鼠与PDX小鼠应用于PK/PD建模时的差异性, 但从已有报道可推测, 与真实肿瘤微环境的相似性使PDX小鼠更适合以剂量预测或临床转化为目的的PK/PD建模[16, 67]; 对真实肿瘤异质性的保留使其可支撑起光化疗这样依赖于真实肿瘤血管环境的复杂载药体的建模[71]。受限于有限的报道、高昂的实验动物成本与仍处于探索中的建模方法, PDX小鼠广泛应用于抗肿瘤药PK/PD建模领域可能仍需漫长的时间。
致谢: 特别感谢研究生曹青青、吴延庆对本课题前期进行的探索性研究工作。
作者贡献:胡宽为本文的第一作者, 负责本文的选题、文献收集及主要内容撰写; 花开负责本文的指导、内容把关与修改; 杨劲为本文的通讯作者, 负责本文的选题、框架设计、指导、修改以及内容把关。
利益冲突:作者声明无利益冲突。
| [1] |
Liu DY, Wang K, Ma GL, et al. The value and general consideration of pharmacometric study in new drug development[J]. Chin J Clin Pharm Ther (中国临床药理学与治疗学), 2018, 23: 961-973. |
| [2] |
Chen WJ, Zhou TY, Lu W. Population pharmacokinetics and its application in new drug research[J]. Acta Pharm Sin (药学学报), 2017, 52: 371-377. |
| [3] |
Shang DW, Wang XP, Deng CH, et al. Application of pharmacometrics in drug development and therapeutic drug monitoring[J]. J Chin Pharm Univ (中国药科大学学报), 2010, 41: 91-96. |
| [4] |
Huang JH, Wang SY, Guan YP, et al. Application progress of population pharmacokenitics/pharmacodymanics modeling in clinical development of anti-cancer drugs[J]. Chin J Clin Pharmacol (中国临床药理学), 2019, 35: 2930-2933. |
| [5] |
Chen Y, Zhao KJ, Liu F, et al. Predicting antitumor effect of deoxypodophyllotoxin in NCI-H460 tumor-bearing mice on the basis of in vitro pharmacodynamics and a physiologically based pharmacokinetic-pharmacodynamic model[J]. Drug Metab Dispos, 2018, 46: 897-907. DOI:10.1124/dmd.117.079830 |
| [6] |
Kelland LR. "Of mice and men":values and liabilities of the athymic nude mouse model in anticancer drug development[J]. Eur J Cancer, 2004, 40: 827-836. DOI:10.1016/j.ejca.2003.11.028 |
| [7] |
Ruggeri BA, Camp F, Miknyoczki S. Animal models of disease:pre-clinical animal models of cancer and their applications and utility in drug discovery[J]. Biochem Pharmacol, 2014, 87: 150-161. DOI:10.1016/j.bcp.2013.06.020 |
| [8] |
Jiang W, Kim S, Zhang X, et al. The role of predictive biopharmaceutical modeling and simulation in drug development and regulatory evaluation[J]. Int J Pharm, 2011, 418: 151-160. DOI:10.1016/j.ijpharm.2011.07.024 |
| [9] |
Sheiner LB, Steimer JL. Pharmacokinetic/pharmacodynamic modeling in drug development[J]. Annu Rev Pharmacol Toxicol, 2000, 40: 67-95. DOI:10.1146/annurev.pharmtox.40.1.67 |
| [10] |
Rocchetti M, Poggesi I, Germani M, et al. A pharmacokinetic-pharmacodynamic model for predicting tumour growth inhibition in mice:a useful tool in oncology drug development[J]. Basic Clin Pharmacol, 2005, 96: 265-268. DOI:10.1111/j.1742-7843.2005.pto960325.x |
| [11] |
Li JY, Ren YP, Yuan Y, et al. Preclinical PK/PD model for combined administration of erlotinib and sunitinib in the treatment of A549 human NSCLC xenograft mice[J]. Acta Pharm Sin (药学学报), 2016, 37: 930-940. DOI:10.1038/aps.2016.55 |
| [12] |
Tate SC, Cai S, Ajamie RT, et al. Semi-mechanistic pharmacokinetic/pharmacodynamic modeling of the antitumor activity of LY2835219, a new cyclin-dependent kinase 4/6 inhibitor, in mice bearing human tumor xenografts[J]. Clin Cancer Res, 2014, 20: 3763-3774. |
| [13] |
Chen WJ, Chen R, Li J, et al. Pharmacokinetic/pharmacodynamic modeling of schedule-dependent interaction between docetaxel and cabozantinib in human prostate cancer xenograft models[J]. J Pharmacol Exp Ther, 2018, 364: 13-25. DOI:10.1124/jpet.117.243931 |
| [14] |
Li MY, Li HQ, Cheng XL, et al. Preclinical pharmacokinetic/pharmacodynamic models to predict schedule-dependent interaction between erlotinib and gemcitabine[J]. Pharm Res, 2013, 30: 1400-1408. DOI:10.1007/s11095-013-0978-7 |
| [15] |
Gu Y, Sai Y, Wang J, et al. Preclinical pharmacokinetics, disposition, and translational pharmacokinetic/pharmacodynamic modeling of savolitinib, a novel selective cMet inhibitor[J]. Eur J Pharm Sci, 2019, 136: 104938. DOI:10.1016/j.ejps.2019.05.016 |
| [16] |
Yao Y, Yao QY, Fu Y, et al. Pharmacokinetic/pharmacodynamic modeling of the anti-cancer effect of dexamethasone in pancreatic cancer xenografts and anticipation of human efficacious doses[J]. J Pharm Sci, 2020, 109: 1169-1177. DOI:10.1016/j.xphs.2019.10.035 |
| [17] |
Ye SF, Li J, Ji SM, et al. Dose-biomarker-response modeling of the anticancer effect of ethaselen in a human non-small cell lung cancer xenograft mouse model[J]. Acta Pharmcol Sin, 2017, 38: 223-232. DOI:10.1038/aps.2016.114 |
| [18] |
Lobo ED, Balthasar JP. Pharmacodynamic modeling of chemotherapeutic effects:application of a transit compartment model to characterize methotrexate effects in vitro[J]. AAPS PharmSci, 2002, 4: 212-222. DOI:10.1208/ps040442 |
| [19] |
Jusko WJ. Pharmacodynamics of chemotherapeutic effects:dose-time-response relationships for phase-nonspecific agents[J]. J Pharm Sci, 1971, 60: 892-895. DOI:10.1002/jps.2600600618 |
| [20] |
Simeoni M, Magni P, Cammia C, et al. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents[J]. Cancer Res, 2004, 64: 1094-1101. DOI:10.1158/0008-5472.CAN-03-2524 |
| [21] |
Yamazaki S, Leslie N, Vekich S, et al. Pharmacokinetic-pharmacodynamic modeling of biomarker response and tumor growth inhibition to an orally available heat shock protein 90 inhibitor in a human tumor xenograft mouse model[J]. J Pharmacol Exp Ther, 2011, 338: 964-973. DOI:10.1124/jpet.111.181339 |
| [22] |
Laird AK. Dynamics of tumour growth:comparison of growth rates and extrapolation of growth curve to one cell[J]. Br J Cancer, 1965, 19: 278-291. DOI:10.1038/bjc.1965.32 |
| [23] |
Koch G, Walz A, Lahu G, et al. Modeling of tumor growth and anticancer effects of combination therapy[J]. J Pharmacokinet Phar, 2009, 36: 179-197. DOI:10.1007/s10928-009-9117-9 |
| [24] |
Li J, Chen R, Yao QY, et al. Time-dependent pharmacokinetics of dexamethasone and its efficacy in human breast cancer xenograft mice:a semi-mechanism-based pharmacokinetic/pharmacodynamic model[J]. Acta Pharmcol Sin, 2018, 39: 472-481. DOI:10.1038/aps.2017.153 |
| [25] |
Yao QY, Li J, Chen R, et al. Preclinical PK/PD model for the combinatorial use of dexamethasone and sulpiride in the treatment of breast cancer[J]. Acta Pharmcol Sin, 2019, 40: 1596-1602. DOI:10.1038/s41401-019-0251-7 |
| [26] |
Yuan Y, Zhou X, Ren Y, et al. Semi-mechanism-based pharmacokinetic/pharmacodynamic model for the combination use of dexamethasone and gemcitabine in breast cancer[J]. J Pharm Sci, 2015, 104: 4399-4408. DOI:10.1002/jps.24629 |
| [27] |
Wang LJ, Lu W, Zhou TY. Current applications of dexamethasone for cancer treatment[J]. Acta Pharm Sin (药学学报), 2015, 50: 1217-1224. |
| [28] |
Jusko WJ. A pharmacodynamic model for cell-cycle-specific chemotherapeutic agents[J]. J Pharmacokinet Biopharm, 1973, 1: 175-200. DOI:10.1007/BF01062346 |
| [29] |
Yates JWT, Holt SV, Logie A, et al. A pharmacokinetic-pharmacodynamic model predicting tumour growth inhibition after intermittent administration with the mTOR kinase inhibitor AZD8055[J]. Br J Pharmacol, 2017, 174: 2652-2661. DOI:10.1111/bph.13886 |
| [30] |
Mager DE, Jusko WJ. Pharmacodynamic modeling of time-dependent transduction systems[J]. Clin Pharmacol Ther, 2001, 70: 210-216. DOI:10.1067/mcp.2001.118244 |
| [31] |
Yang J, Mager DE, Straubinger RM. Comparison of two pharmacodynamic transduction models for the analysis of tumor therapeutic responses in model systems[J]. AAPS J, 2010, 12: 1-10. DOI:10.1208/s12248-009-9155-7 |
| [32] |
Ji XW, Ji SM, Li RT, et al. Pharmacokinetic-pharmacodynamic modeling of the antitumor effect of TM208 and EGFR-TKI resistance in human breast cancer xenograft mice[J]. Acta Pharm Sin (药学学报), 2016, 37: 825-833. DOI:10.1038/aps.2016.40 |
| [33] |
Wu Q, Li MY, Li HQ, et al. Pharmacokinetic-pharmacodynamic modeling of the anticancer effect of erlotinib in a human non-small cell lung cancer xenograft mouse model[J]. Acta Pharmcol Sin, 2013, 34: 1427-1436. DOI:10.1038/aps.2013.101 |
| [34] |
Wang SY, Zhu X, Han MY, et al. Mechanistic pharmacokinetic/pharmacodynamic model of sunitinib and dopamine in MCF-7/Adr xenografts:linking cellular heterogeneity to tumour burden[J]. AAPS J, 2020, 22: 45-57. DOI:10.1208/s12248-020-0428-5 |
| [35] |
Pigatto MC, Roman RM, Carrara L, et al. Pharmacokinetic/pharmacodynamic modeling of etoposide tumor growth inhibitory effect in Walker-256 tumor-bearing rat model using free intratumoral drug concentrations[J]. Eur J Pharm Sci, 2017, 97: 70-78. DOI:10.1016/j.ejps.2016.10.038 |
| [36] |
Goteti K, Garner CE, Utley L, et al. Preclinical pharmacokinetic/pharmacodynamic models to predict synergistic effects of co-administered anti-cancer agents[J]. Cancer Chemother Pharm, 2010, 66: 245-254. DOI:10.1007/s00280-009-1153-z |
| [37] |
Rocchetti M, Simeoni M, Pesenti E, et al. Predicting the active doses in humans from animal studies:a novel approach in oncology[J]. Eur J Cancer, 2007, 43: 1862-1868. DOI:10.1016/j.ejca.2007.05.011 |
| [38] |
Li MY. Pharmacokinetic/Pharmacodynamic Models of Schedule-Dependent Interaction of Erlotinib and Gemcitabine (埃罗替尼与吉西他滨不同给药方案联用的药代动力学与药效动力学研究)[D]. Beijing: Peking University, 2012.
|
| [39] |
Davies AM, Ho C, Lara PN, et al. Pharmacodynamic separation of epidermal growth factor receptor tyrosine kinase inhibitors and chemotherapy in non-small-cell lung cancer[J]. Clin Lung Cancer, 2006, 7: 385-388. DOI:10.3816/CLC.2006.n.021 |
| [40] |
Li TH, Ling YH, Goldman ID, et al. Schedule-dependent cytotoxic synergism of pemetrexed and erlotinib in human non-small cell lung cancer cells[J]. Clin Cancer Res, 2007, 13: 3413-3422. DOI:10.1158/1078-0432.CCR-06-2923 |
| [41] |
Morelli MP, Cascone T, Troiani T, et al. Sequence-dependent antiproliferative effects of cytotoxic drugs and epidermal growth factor receptor inhibitors[J]. Ann Oncol, 2005, 16: 61-68. |
| [42] |
Dayneka NL, Garg V, Jusko WJ. Comparison of 4 basic models of indirect pharmacodynamic responses[J]. J Pharmacokinet Biopharm, 1993, 21: 457-478. DOI:10.1007/BF01061691 |
| [43] |
Sheiner LB, Stanski DR, Vozeh S, et al. Simultaneous modeling of pharmacokinetics and pharmacodynamics:application to d-tubocurarine[J]. Clin Pharmacol Ther, 1979, 25: 358-371. DOI:10.1002/cpt1979253358 |
| [44] |
Zhang W, Zheng X, Wang X. Oxidative stress measured by thioredoxin reductase level as potential biomarker for prostate cancer[J]. Am J Cancer Res, 2015, 5: 2788-2798. |
| [45] |
Bueno L, De Alwis DP, Pitou C, et al. Semi-mechanistic modelling of the tumour growth inhibitory effects of LY2157299, a new type I receptor TGF-beta kinase antagonist, in mice[J]. Eur J Cancer, 2008, 44: 142-150. DOI:10.1016/j.ejca.2007.10.008 |
| [46] |
Adorno-Cruz V, Kibria G, Liu X, et al. Cancer stem cells:targeting the roots of cancer, seeds of metastasis, and sources of therapy resistance[J]. Cancer Res, 2015, 75: 924-929. DOI:10.1158/0008-5472.CAN-14-3225 |
| [47] |
Ablett MP, Singh JK, Clarke RB. Stem cells in breast tumours:are they ready for the clinic?[J]. Eur J Cancer, 2012, 48: 2104-2116. DOI:10.1016/j.ejca.2012.03.019 |
| [48] |
Sachlos E, Risueno RM, Laronde S, et al. Identification of drugs including a dopamine receptor antagonist that selectively target cancer stem cells[J]. Cell, 2012, 149: 1284-1297. DOI:10.1016/j.cell.2012.03.049 |
| [49] |
Wang SY, Mou ZZ, Ma YH, et al. Dopamine enhances the response of sunitinib in the treatment of drug-resistant breast cancer:Involvement of eradicating cancer stem-like cells[J]. Biochem Pharmacol, 2015, 95: 98-109. DOI:10.1016/j.bcp.2015.03.013 |
| [50] |
Hao FR, Wang SY, Zhu X, et al. Pharmacokinetic-pharmacodynamic modeling of the anti-tumor effect of sunitinib combined with dopamine in the human non-small cell lung cancer xenograft[J]. Pharm Res, 2017, 34: 408-418. DOI:10.1007/s11095-016-2071-5 |
| [51] |
Ma YH, Wang SY, Ren YP, et al. Antitumor effect of axitinib combined with dopamine and PK-PD modeling in the treatment of human breast cancer xenograft[J]. Acta Pharmcol Sin, 2019, 40: 243-256. DOI:10.1038/s41401-018-0006-x |
| [52] |
Chinchar E, Makey KL, Gibson J, et al. Sunitinib significantly suppresses the proliferation, migration, apoptosis resistance, tumor angiogenesis and growth of triple-negative breast cancers but increases breast cancer stem cells[J]. Vasc Cell, 2014, 6: 12. DOI:10.1186/2045-824X-6-12 |
| [53] |
Conley SJ, Gheordunescu E, Kakarala P, et al. Antiangiogenic agents increase breast cancer stem cells via the generation of tumor hypoxia[J]. Proc Natl Acad Sci U S A, 2012, 109: 2784-2789. DOI:10.1073/pnas.1018866109 |
| [54] |
Mackey JR, Kerbel RS, Gelmon KA, et al. Controlling angiogenesis in breast cancer:a systematic review of anti-angiogenic trials[J]. Cancer Treat Rev, 2012, 38: 673-688. DOI:10.1016/j.ctrv.2011.12.002 |
| [55] |
Wang L, Yang Z, Fu J, et al. Ethaselen:a potent mammalian thioredoxin reductase 1 inhibitor and novel organoselenium anticancer agent[J]. Free Radic Bio Med, 2012, 52: 898-908. DOI:10.1016/j.freeradbiomed.2011.11.034 |
| [56] |
Wong H, Vernillet L, Peterson A, et al. Bridging the gap between preclinical and clinical studies using pharmacokinetic-pharmacodynamic modeling:an analysis of GDC-0973, a MEK inhibitor[J]. Clin Cancer Res, 2012, 18: 3090-3099. DOI:10.1158/1078-0432.CCR-12-0445 |
| [57] |
Salphati L, Wong H, Belvin M, et al. Pharmacokinetic-pharmacodynamic modeling of tumor growth inhibition and biomarker modulation by the novel phosphatidylinositol 3-kinase inhibitor GDC-0941[J]. Drug Metab Dispos, 2010, 38: 1436-1442. DOI:10.1124/dmd.110.032912 |
| [58] |
Chen DS, Huang P. Clinical Pharmacokinetics and Pharmacodynamics:Concepts and Applications (临床药代动力学与药效动力学)[M]. 4th Ed. Beijing: People's Medical Publishing House, 2012.
|
| [59] |
Yamazaki S, Vicini P, Shen Z, et al. Pharmacokinetic/pharmacodynamic modeling of crizotinib for anaplastic lymphoma kinase inhibition and antitumor efficacy in human tumor xenograft mouse models[J]. J Pharmacol Exp Ther, 2012, 340: 549-557. DOI:10.1124/jpet.111.188870 |
| [60] |
Yamazaki S, Skaptason J, Romero D, et al. Pharmacokinetic-pharmacodynamic modeling of biomarker response and tumor growth inhibition to an orally available cMet kinase inhibitor in human tumor xenograft mouse models[J]. Drug Metab Dispos, 2008, 36: 1267-1274. DOI:10.1124/dmd.107.019711 |
| [61] |
Li P, Li S, Gu H, et al. The exposure-effect-toxicity correlation of docetaxel and magnesium isoglycyrrhizinate in non-small cell lung tumor-bearing mice[J]. Biomed Pharmacother, 2018, 97: 1000-1010. DOI:10.1016/j.biopha.2017.10.158 |
| [62] |
Wong H, Gould SE. Translational pharmacokinetic/pharmacodynamic analysis in cancer pharmacology:a tool to maximize the value of antitumor efficacy from tumor bearing mice[J]. Drug Discov Today Technol, 2016, 21-22: 51-56. DOI:10.1016/j.ddtec.2016.08.003 |
| [63] |
Eigenmann MJ, Frances N, Hoffmann G, et al. Combining nonclinical experiments with translational PKPD modeling to differentiate erlotinib and gefitinib[J]. Mol Cancer Ther, 2016, 15: 3110-3119. DOI:10.1158/1535-7163.MCT-16-0076 |
| [64] |
Wong H, Choo EF, Alicke B, et al. Antitumor activity of targeted and cytotoxic agents in murine subcutaneous tumor models correlates with clinical response[J]. Clin Cancer Res, 2012, 18: 3846-3855. DOI:10.1158/1078-0432.CCR-12-0738 |
| [65] |
He H, Zhang X, Wang YH, et al. Advances in pharmacokinetic and pharmacodynamic modeling of monoclonal antibody[J]. J Chin Pharm Univ (中国药科大学学报), 2015, 46: 279-288. |
| [66] |
Shah DK, Haddish-Berhane N, Betts A. Bench to bedside translation of antibody drug conjugates using a multiscale mechanistic PK/PD model:a case study with brentuximab-vedotin[J]. J Pharmacokinet Pharmacodyn, 2012, 39: 643-659. DOI:10.1007/s10928-012-9276-y |
| [67] |
Singh R, Kozhich A, Pan C, et al. A novel semi-mechanistic tumor growth fraction model for translation of preclinical efficacy of anti-glypican 3 antibody drug conjugate to human[J]. Biopharm Drug Dispos, 2020. DOI:10.1002/bdd.2249 |
| [68] |
Fetterly GJ, Aras U, Meholick PD, et al. Utilizing pharmacokinetics/pharmacodynamics modeling to simultaneously examine free CCL2, total CCL2 and carlumab (CNTO 888) concentration time data[J]. J Clin Pharmacol, 2013, 53: 1020-1027. DOI:10.1002/jcph.140 |
| [69] |
Hidalgo M, Amant F, Biankin AV, et al. Patient-derived xenograft models:an emerging platform for translational cancer research[J]. Cancer Discov, 2014, 4: 998-1013. DOI:10.1158/2159-8290.CD-14-0001 |
| [70] |
Cassidy JW, Caldas C, Bruna A. Maintaining tumor heterogeneity in patient-derived tumor xenografts[J]. Cancer Res, 2015, 75: 2963-2968. DOI:10.1158/0008-5472.CAN-15-0727 |
| [71] |
Luo D, Carter KA, Molins EAG, et al. Pharmacokinetics and pharmacodynamics of liposomal chemophototherapy with short drug-light intervals[J]. J Control Release, 2019, 297: 39-47. DOI:10.1016/j.jconrel.2019.01.030 |
 2020, Vol. 55
2020, Vol. 55


