2. 昆明理工大学信息工程与自动化学院, 云南 昆明 650500
2. Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650500, China
中药, 特别是中药复方, 是一类公认的复杂系统。传统中药以单味药为基本单元, 按照配伍规律组成整体方剂进行疾病的防治。现代中药研究者更多地从分子水平(化学成分)研究中药复杂系统, 概括出中药“多成分、多靶点”的作用特点。经过近90年的发展, 利用现代科学技术, 研究者对中药复杂系统的化学成分组成和作用靶点有了越来越清晰、精细的认识, 也诞生了“组分中药”[1-4]、“中药有效成分组”[5]等化学组成较清晰、作用靶点较明确的新型中药复杂系统。
中药复杂体系除了明确系统组成成分外, 需要进一步研究其内在组合规律。传统的“君臣佐使”和“七情”配伍, 阐述的是单味药层次上的中药方剂配伍的规律。现在, 中药复杂系统研究逐渐进入在化学成分(分子)水平研究中药复杂系统的整体动态变化和运行规律的研究阶段, 需要阐明系统内部的结构和各个成分之间的相互关系, 通过阐明各个成分、局部集合(有效部位)间相互关系, 阐述中药复杂系统的整体性[6]。这方面, 研究者们提出一些假说, 如中药整合药代动力学方法[7]、总量矩[8]、中药显效理论[9]、网通虹势理论[10]、网络代谢理论[11]、中药方证代谢组学[12]、网络药动学[13]和网络药理学[14]等。这些理论均在一定程度上表征了中药复杂系统的整体性特征, 但仍需要将理论计算结果与实验测定值进行比较印证, 验证假说。故本文基于多年来的实验观察和文献总结, 提出中药复杂系统的“多源归一”假说及其数学模型, 以及检验假说可能的思路、实验技术方法和部分证据, 希望能推进中药复杂系统的研究理论。
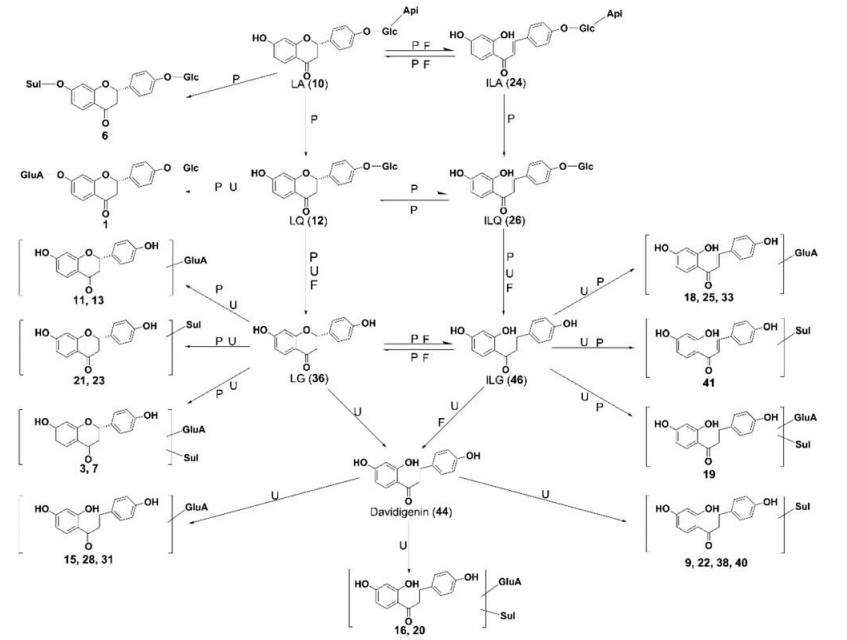
1 “多源归一”假说的提出作者首先在甘草多成分药物代谢研究过程中, 注意到甘草中黄酮类多个成分可以产生相同代谢产物的现象(图 1)[15], 进一步的多成分药物动力学研究发现各个成分的药物动力学规律存在某种联系[16], 推测此现象在其他中药, 如灯盏花、青阳参中也存在, 初步提出了“多源归一”假说。经过几年的研究, 逐步完善了该假说并进行了一定的实践检验。
|
Figure 1 In vivo metabolic network of flavonoids in licorice [15] |
中药复杂系统的“多源归一”假说可以表述为:在中药混合物复杂系统中, 同一活性成分或(和)同一个生物效应可以由多个相互关联的来源产生。该假说的特征有以下3点: ①假说研究对象是混合物, 即中药混合物复杂系统, 而不是单体化合物, 区别于现代的主流化学药、生物药和天然药物化学的单一药效分子。中药混合物复杂系统可以是多味中药组成的中药复方, 也可以是单味药中多个化学成分, 甚至是组分中药的有限的两个或两个以上的成分; ②研究的层次应该是在具体中药成分, 即分子水平进行研究, 而非在单味药水平或有效部位进行研究; ③假说研究重点是一种中药复杂系统中特殊的相互作用及其规律。
按照药物发挥作用的时相划分, “多源归一”有3种可能的情况: ①中药复方中, 同一个化学成分可能来自于两种或两种以上的药味, 即药剂相的多源归一; ②中药复方或单方中, 体内的同一个中药成分可能由两个或两个以上的化学结构相关的(如苷元)的原型成分吸收、代谢而来, 即药动相的多源归一; ③中药复方或单方中, 中药复杂系统的同一个生物效应可能由两个或两个以上的成分共同作用产生, 即药效相的多源归一。
3 检验“多源归一”假说的基本要求、基本模型、可能的技术方法和部分例证 3.1 论证“多源归一”假说的基本要求“多源归一”假说的研究对象是中药复杂系统中一类特殊的相互作用, 该假说的证明应遵循科学假说检验的基本规则。按照系统科学理论, 若要检验该假说是否正确, 则需要先掌握单体化合物的特点, 再说明有多源归一现象的中药复杂系统的整体性、各个要素的相关性、系统内结构的层次性和有序性, 以及系统的动态变化规律[6]。
从科学论证方法的角度, 要检验“多源归一”假说是否正确, 首先应该判断假说的提出是否依据科学事实, 然后可以采用归纳法, 从中药多源归一的科学实例中摸索规律, 提出模型(包括系统结构模型、数学模型、动物模型)进行仿真, 进而采用演绎法, 在“多源归一”理论假说的指导下, 用实验法或观察法验证理论是否与事实相符, 甚至预测未来发展。在论证过程中, 应该将抽象模型和具体实例相结合, 将定性与定量相结合。在演绎过程中, 案例研究(枚举法)是较可行的, 穷举法和反证法是比较困难, 而根据理论假说, 预测具体案例的未来发展并得到实践的检验, 将是对该假说的最有力的论证。当然, 多源归一不是普适理论假说, 的确可能存在不成立的情况, 然而目前该假说刚刚提出, 系统研究案例还非常少, 需要在今后的研究中不仅积累假说成立的案例, 也要积累不成立的案例, 进而分析该假说成立的前提条件, 确定假说成立的外延, 这也是进一步研究该假说的重要内容之一。
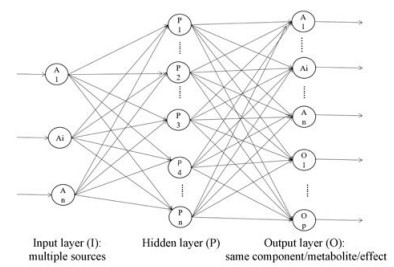
3.2 “多源归一”假说的基本模型根据“多源归一”假说的概念和甘草化合物体内代谢的实验结果, 该假说可以用人工神经网络(artificial neural network, ANN)作为基本的结构和数学模型, 进行数学模拟, 其模型结构如图 2。
|
Figure 2 Artificial neural network model of the hypothesis of one output multi-source for traditional Chinese medicine complex system |
ANN是一种多层前馈网络, 是一种人工智能算法, 采用典型的、有指导学习的方式来进行预测和分类问题的处理。一个训练好的ANN, 理论上能够逼近任何自变量的网络输入和应变量的网络输出之间的函数关系。该模型在应用中可以识别变量间任意复杂的线性或非线性关系, 尤其是用现有的数学方法无法达到目的时, 采用神经网络模型往往能收到很好的效果。
中药复杂系统多源归一可符号化描述为一个三元组ANN (I, P, O), 其中, I为输入层: I = {Ai|i∈1…N}。在药剂相, Ai为各味药材中各成分的含量; 在药动相, Ai为给予机体的原型化合物的剂量; 在药效相, Ai为共同起效的有效成分的血药浓度或靶器官的浓度。P为隐含层: P = {(Ai, Mj)|i∈1…N, j∈1…P}, Ai和Mj为相互作用过程中的中间过渡态, 如药效相的蛋白-化合物复合物, 药动相的转运体-化合物结合态、代谢中间体, Ai为原型化合物, Mj为转化产物。O为输出层: O = {[Ai, Mj]| i∈1…N, j∈1…P}, 在药剂相, Ai为最终释放池的终浓度; 在药动相, Ai, Mj为原型和共同代谢产物的血药浓度; 在药效相, Ai, Mj为整体表现出来的多方面的生物效应。
将实验观测到的样本分为训练集和测试集两部分, 通过ANN学习输入-输出预测模型, 并将测试集的预测结果与实际观测结果进行检验分析, 可以验证模型的准确性。进而, 当输入药物剂量或其他输入参数发生变化时, 就可以预测出相应的溶出量、血药浓度或药效强度。这对于通过调节不同成分的配伍、控制溶出或药效强度具有实际指导意义。
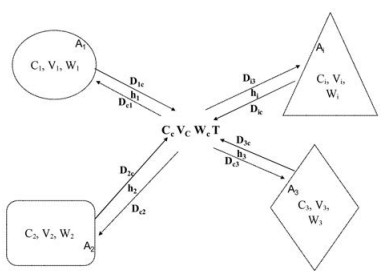
3.3 不同时相的中药复杂系统“多源归一”假说的部分检验 3.3.1 药剂相的多源归一模型和检验在药剂相, 中药复方的多源归一问题即为中药复方的混合提取时, 同一个化学成分从不同药材中溶出的问题。一个中药复方中两味药含有相同的化学成分在实际情况中是存在的, 如四物汤(熟地、川芎、丹参、当归)中川芎和当归均含有阿魏酸和川芎嗪。药剂相多源归一现象的存在, 导致了复方煎煮与单味药煎煮有可能出现不同、有相互作用现象。付绍平等[17]在四物汤的研究中, 对比当归、川芎单煎和合煎, 发现川芎嗪基本上是加和作用, 而合煎的阿魏酸溶出量比单煎的有所增加, 存在着相互作用。这些实例定性说明了中药复方药剂相“多源归一”假说是成立的, 据此和多源归一的ANN模型, 抽象出中药复方药剂相的“多源归一”的结构模型(图 3)。
|
Figure 3 Schematic diagram of multi-source normalization of the Chinese medicine compound. The compound contains herbs A1, A2, A3, …, Ai (indicated by different shape boxes), all of which contain the same component W, Ci is the concentration of the component W contained in the medicinal material i, and Vi is the internal volume of the medicinal material. During the boiling process, W is released to the central compartment Wc, and T is the boiling temperature |
定量证明药剂相的“多源归一”假说, 可以对中药材溶出(提取)的动力学过程进行数学仿真研究。针对中药单味药化学成分的提取和溶出, Spiro等[18-20]、储茂泉等[21]、贺福元等[22]和王伯初等[23]都基于Fick传质定律提出了动力学模型, 考虑了药材内部的扩散、结构、粒度、吸附和成分降解, 以及外部溶剂种类、温度、溶液黏度、溶剂量、封闭系统(如回流、超声)和开放系统(渗漉、索氏提取)等一系列因素。然而, 中药复方的提取和单味药的提取常常不同[24, 25], 复方提取需要用系统思想, 考虑药材多组分间传质, 阐明中药复方提取的整体性、关联性和动态性[26, 27]。故基于以上的研究和多源归一的ANN模型, 中药复方药剂相的多源归一结构模型可以表达为图 3。
结合王伯初等[23]的动力学表达式和吸收-排除关系算法, 参考药动学的隔室模型, 可以推出含有同一个成分A的两味药材(A1、A2)共提取, 提取液中某共同成分浓度Cc随时间t的数学关系为:
| $C\left( t \right) = \gamma \left( {{{\rm{e}}^{ - \alpha t}} - {{\rm{e}}^{ - \beta t}}} \right)$ |
其中, α为一级释放常数, β为反向吸附常数,
| $\left\{ {\begin{array}{*{20}{c}} {{\rm{C}}\left( t \right) = \mathop \smallint \limits_0^t \alpha {C_{{\rm{in}}}}\left( t \right){\rm{dt}} - \mathop \smallint \limits_0^t \beta C\left( t \right){\rm{dt}}}\\ {{C_{{\rm{in}}}}\left( t \right) = {\rm{F}}{C_0} - \mathop \smallint \limits_0^{\rm{t}} \alpha {C_{{\rm{in}}}}\left( t \right){\rm{dt}}} \end{array}} \right.$ |
其中, F为释放率, 且满足
在药效相检验“多源归一”假说, 即要证明中药复杂系统中, 两个或两个以上的化合物联合应用时表现出综合的整体生物效应。这里的生物效应可以是基因、蛋白等分子水平, 也可以是细胞、组织、器官和整体动物, 甚至临床的表观效应。对于中药复杂系统中多个化合物联合发挥生物效应, 其相互作用关系有以下3种情况:第1种, 成分A和B均有同种生物效应, A+B后产生协同(synergism)、加和(additive effect)或拮抗(antagonism)效应; 第2种, A有生物效应, B无, A+B后放大A的生物效应; 第3种, A和B均无生物效应, A+B产生新的产物C, C直接产生生物效应。这是分子水平的“七情”配伍, 其中“相须”、“相使”和第1、2种中的放大效应、协同效应、加和效应, 以及第3种的形成产物C类似; “相畏”、“相杀”与第2种的拮抗效应类似; “相恶”与第2种的毒性协同或加和效应类似。
对于第1种相互关系, 已经有大量的科学事实证实其存在, 即1味中药中的化学成分, 如槐米中的黄酮、三七中的皂苷和黄连中的生物碱, 同类成分都具有相似的生理活性; 对于中药复杂系统, 相当于1个靶点由多个分子作用, 从定性的角度验证了中药复杂系统的药效相多源归一的存在可能性, 这与罗国安等[28]的“有效部位”、蔡少青提出的“显效理论”[9]等一致。对于第1种相互作用的定量研究, 其基本研究思路和方法可以采用经典的“药物联合指数” (combination Index, CI)法[29]。该方法基于物理化学的“质量作用定律” (mass-action law), 整合了Michaelis-Menten、Hill、Henderson-Hasselbalch和Scatchard方程, 首先表达了单一化合物作用的“剂量-效应”关系的中位效应(median effect)方程:
| $\frac{{fa}}{{fu}} = {\left[ {\frac{D}{{{D_m}}}} \right]^m}$ |
其中, fa为化合物已经发生的部分效应; fu为还未发生的效应; D为产生fa效应时的剂量; Dm为产生中位效应的剂量, 即IC50、EC50或IC30; 然后, 从两个化合物加和效应入手, Chou[29]建立了两个化合物联合应用的联合指数表达式:
| ${\rm{CI}} = \frac{{\left( D \right)1}}{{\left( {{D_x}} \right)1}} + \frac{{\left( D \right)2}}{{\left( {{D_x}} \right)2}}$ |
其中, (D)1、(D)2为两药联合产生中位效应x时, 每个药物的剂量, (Dx)1、(Dx)2为这两个化合物单独使用时产生中位效应x的剂量; 当CI = 1, 表示两个化合物为加和作用; CI < 1, 表示两个化合物为协同增强效应; CI > 1, 表示两个化合物为拮抗效应。在此基础上, 拓展为多个化合物联合应用的剂量-效应联合指数计算方式:
| $\text{CI}=\sum\limits_{i=1}^{n}{{\frac{\left( D \right)i}{\left( {{D}_{x}} \right)i}}}$ |
基于该数学模型, Chou等[30]开发了CompuSyn软件, 可以用于计算多个药物联用组合在不同效应强度(Fa)下CI值; 结果可以用Fa-CI曲线或Fa-LogCI曲线表示, 两个药物的组合可以使用经典的等效线图(isobologram)表示, 多个药的组合可以用“多效图” (polygonogram)半定量表示。Chou[29]曾利用该方法和软件, 开展了抗艾滋病的五联疗法的药物相互作用研究、7个不同机制的抗肿瘤药物联用的相互作用及在动物模型、甚至临床药物的联用研究。该方法对于药物的作用机制是否清楚没有要求, 组合的生物效应强度可以表示系统整体的效应, CI值可以定量表征多个成分的相互作用关系, 但是能否依靠CI值预测多个药物组合的联合效应强度尚不肯定。该方法现已被广泛应用于生物医学领域, 但在中药复方研究中, Long等[31]采用此法发现复方丹参滴丸中酚酸类、丹参酮类化合物对抗炎有加和作用, 但目前该方法在中药复杂系统研究中应用较少, 亟需推广。
第2种相互作用, 典型的案例有黄芩汤(PHY906)增强抗肿瘤药作用[32]。黄芩汤本身并无抗肿瘤作用, 但与化疗药(如伊立替康)合用后, 可显著增强抗肿瘤效果。其机制可以简述为化疗药物导致肿瘤内部炎症, PHY906放大了炎症细胞对肿瘤细胞的杀伤, 形成了一种正反馈效应。这类相互作用的另一种可能的机制为催化反应, 无效应的B分子是酶催化反应的催化剂或辅酶分子, 其过程应该遵循Michael-Menten方程。目前, 对于中药中这类相互作用规律的定量研究尚未见到非常明确报道。
第3种相互作用的核心是形成了真正效应形式C, 类似于生物化学中的活性效应复合物或激活生物效应通路的多个环节, 进而激活整条通路; 药物化学中由两个前药生成一个体内代谢真正活性形式。这类相互作用是否存在、规律如何还未见到确切的研究报道。
3.3.3 药动相的多源归一模型和检验药动相的多源归一可以表述为体内的某个来自中药的成分有多个来源, 可以既是药材中的原型成分, 又可能是多个类似结构化合物的共同代谢产物, 多源之间存在相互作用。这类现象较为常见, 如Gong等[33]在鉴定脉络宁注射液体内成分(原型、代谢产物)研究中有提及, Chen等[34]在研究普洱茶体内代谢时也遇到。作者在研究甘草入血成分和代谢产物过程中, 特别设计了一系列同母核苷元化合物单用和合用在大鼠体内代谢情况的对比实验, 明确地观察到体内代谢多源归一的现象[15], 在进一步甘草多成分的药物动力学(PK)研究中, 检测了63个原型和代谢产物的体内PK, 得到了55个化合物的药-时曲线; 相比单体, 甘草复杂系统中各成分发生了相互作用, 影响了PK行为, 变化类型有4类:增加了苷元的生物利用度; 延长了苷类成分在体内存在时长; 降低了可能毒性成分浓度; 改变了Ⅱ相代谢反应的类型[16]。李启泉[11]在研究左金丸的整体药代时, 也明确表达了类似多源归一的ANN结构的网络代谢图。以上实例定性检验了药动相多源归一现象是存在的, 该假说与超分子“印迹模板”理论、“网通虹势”理论有相似性和兼容性。然而采用数学方法定量表达药动相的多源归一的变化规律较为困难, 障碍首先在于整体PK的数学表达。多源归一整体PK模型应该做到: ①所选择的指标应可以表达整体, 并有确切可被实践检验的生物学意义; ②可以表现出多成分的特征; ③可以表达出多个成分间的相互关系。目前比较认可的思路是整体生物效应(PD)可以用于检验整体的PK, 即构建整体系统的PK-PD关系, 已有多个研究团队对整体PK、PK-PD进行了研究[13, 35], 其中引入代谢组学表征PD是较为合理的方法[13, 14, 34], 但仍存在一定缺陷。
作者在研究青阳参PK-PD模型时, 首先借鉴了贺福元“总量矩法”[8]、郝海平“整合药代动力学法”[7], 将小鼠灌胃青阳参有效成分组后, t时刻两个化合物的血药浓度进行加和, 成为整体浓度CM12, 并采用一室血管外隔室模型:
| $\left\{ {\begin{array}{*{20}{c}} {{C_{M12}}\left( t \right) = \mathop \smallint \limits_0^t \alpha {C_{{\rm{in}}}}\left( t \right){\rm{dt}} - \mathop \smallint \limits_0^{\rm{t}} \beta C\left( t \right){\rm{dt}}}\\ {{C_{{\rm{M}}12{\rm{in}}}}\left( t \right) = {\rm{F}}{C_0} - \mathop \smallint \limits_0^t \alpha {C_{{\rm{in}}}}\left( t \right){\rm{dt}}} \end{array}} \right.$ |
其中, F是生物利用度, C0为0时刻的体内药物浓度。采用非线性最小二乘法拟合出CM12和t的关系式:
| $ {C_{M12}}\left( t \right){\rm{ }} = \gamma ({{\rm e}^{ - \alpha t}} - {{\rm e}^{ - \beta t}}) $ |
其中, α为吸收相关的系数, β为消除相关的系数, γ为表观分布体积相关参数。采用ANN, 以浓度CM12仿真预测生物效应, 在药物的消除阶段, 有效性预测准确率接近100%, 但在吸收阶段还有一定差距。
作者另一个算法是在整合药代动力学的基础上, 吸收了李川的“中药药代标志物”[36]的思路、并引入联合指数CI, 不同药物生物效应转化系数k, 构建了一个多源归一的整合PK计算方法, 并可以用整体的PD检验整体PK的合理性。以两个化合物a、b联合组成的复杂系统A为例, 说明其基本思路: ①分别通过实验测定a、b的浓度-效应关系, 并采用中位效应方程[29]计算出a、b的Dm (a)和Dm (b); ②计算b与a的生物效应转化系数k (
| $C_{\rm{a}}^{\rm{'}} = \frac{1}{{{\rm{CI}}}}\left( {{C_{\rm{a}}} + k{C_{\rm{b}}}} \right)$ |
此式为复杂系统(a+b)的整合浓度
| $\left\{ {\begin{array}{*{20}{c}} {C_{\rm{a}}^{\rm{'}} = \frac{1}{{{\rm{CI}}}}\left( {{C_{\rm{a}}} + k{C_{\rm{b}}}} \right)}\\ {{f_{{\rm{a 预测}}}} = \frac{1}{{1 + {{\left( {\frac{{C_{\rm{a}}^{\rm{'}}}}{{{D_{m\left( {\rm{a}} \right)}}}}} \right)}^m}}}} \end{array}} \right.$ |
进而可以进行复杂系统的生物效应预测, 并和实验测定的整体效应fa实测比较。若相近则表明
定量表达药动相多源归一的另一个障碍是阐明“多源”之间的相互关系产生的机制, 如在甘草代谢中发现的增加“归一”化合物生物利用度, 延长存在时间, 降低某个成分体内暴露量, 改变代谢反应类型。这部分将涉及较多药物代谢酶、转运体相互作用的研究, 有较为成熟的研究技术, 但是如何将局部的酶反应、转运体的相互作用解释整体PK的变化, 是今后研究的难点内容之一。
4 “多源归一”假说的意义和应用不同于天然药物化学的单体化合物研究模式, “多源归一”假说是研究中药复杂系统中各个化学成分之间的相互关系, 通过该假说的研究, 在分子水平加深对中药配伍的认识, 加深对中药复杂系统的认识, 有一定的理论意义。因其研究重点是有密切关联的一组有效成分, 且所采用的人工神经网络模型有学习、预测能力, 故可以指导更加科学合理的中药配伍优化、组分中药的研发和中药饮片配方颗粒生产, 故该假说还有一定的实际应用意义。更广阔地, 因为中药复杂体系的“多源归一”假说是分子水平的研究, 与现代化学药、生物药处于相同的维度, 故其规律可以成为容纳西药和中药在内的多分子药物组合的研究理论基础假说, 为人类对抗疾病创造出上亿种药物组合, 促进新疗法的出现。当然, 该假说还处于初期概念阶段, 很不完善, 检验、证明还面临许多挑战, 也需要在不断检验过程中修正, 最终成为多分子混合复杂体系的研究理论。
| [1] | Miao MS, Ma RJ, Wei RR, et al. Research technique and consideration the proportion of the TCM components[J]. J Henan Univ (Med Sci) (河南大学学报(医学版)), 2011, 30: 1–5. |
| [2] | Ye ZG. Multi-ingredient traditional Chinese medicines preparations and their effective fractions[J]. Chin J New Drugs (中国新药杂志), 2011, 20: 1487–1489. |
| [3] | Liang XM, Xu Q, Xue XY, et al. Systematic research on the multi-component Chinese medicine[J]. World Sci Technol-Modern Tradit Chin Med Mater Med (世界科学技术-中医药现代化), 2006, 8: 1–7. |
| [4] | Fu JH, Fu Y, Liu JX. Conception of TCD component hypothesis[J]. Chin J Inform TCM (中国中医药信息杂志), 2006, 13: 52–54. |
| [5] | Kong L, Li BC, Xiang C. Research progress on effective compounds group of Chinese materia medica[J]. Chin Tradit Herb Drugs (中草药), 2015, 46: 3289–3296. |
| [6] | Wang YL. Systems Engineering (系统工程)[M]. 4th ed. Beijing: Mechanical Industry Press, 2008. |
| [7] | Hao HP, Zheng CN, Wang GJ. Thoughts and experimental exploration on pharmacokinetic study of herbal medicines with multiple-components and targets[J]. Acta Pharm Sin (药学学报), 2009, 44: 270–275. |
| [8] | He FY, Luo WJ, Deng KW, et al. A survey on status and research method of pharmacokinetics of formula Chinese materia medica[J]. Chin Tradit Herb Drugs (中草药), 2005, 36: 1582–1586. |
| [9] | Xu F, Yang DH, Shang MY, et al. Effective forms, additive effect, and toxicities scattering effect of pharmacodynamic substances of TCMs some reflections evoked by the study on the metabolic disposition of traditional chinese medicines (TCM)[J]. World Sci Technol-Modern Tradit Chin Med Mater Med (世界科学技术-中医药现代化), 2014, 16: 688–703. |
| [10] | He FY, Deng KW, Liu WL, et al. Reactive essence between Chinese materia medica formula and human body:multiple genetic chromatodynamokinetics with 'Co-network Compatibility and Rainbow Potential'[J]. Chin J Exp Tradit Med Formu (中国实验方剂学杂志), 2011, 17: 240–247. |
| [11] | Li QQ. Zuo Jinfang Multi-alkali In Vivo Network Metabolism " Rain Potential" Research (左金方多生物碱体内网络代谢"虹势性"研究)[D]. Changsha: Hunan University of Chinese Medicine, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10541-2009243292.htm |
| [12] | Kang SY, Zhang JQ, Zhang AJ, et al. Based on urine metabolomics to study effect of Liuwei Dihuang Wan on growth and development of rats[J]. Acta Pharm Sin (药学学报), 2018, 53: 1713–1720. |
| [13] | Xiang Z, Cai XJ, Zeng S. Thoughts and exploration on pharmacokinetic study of herbal medicines based on metabonomics and complex network[J]. Acta Pharm Sin (药学学报), 2012, 47: 558–564. |
| [14] | Pang XC, Wang Z, Fang JS, et al. Network pharmacology study of effective constituents of traditional Chinese medicine for Alzheimer's disease treatment[J]. Acta Pharm Sin (药学学报), 2016, 51: 725–731. |
| [15] | Xiang C, Qiao X, Wang Q, et al. From single compounds to herbal extract:a strategy to systematically characterize the metabolites of licorice in rats[J]. Drug Metabol Disposit, 2011, 39: 1597–1608. DOI:10.1124/dmd.111.038695 |
| [16] | Qiao X, Ye M, Xiang C, et al. Analytical strategy to reveal the in vivo process of multi-component herbal medicine:a pharmacokinetic study of licorice using liquid chromatography coupled with triple quadrupole mass spectrometry[J]. J Chromatogr A, 2012, 1258: 84–93. DOI:10.1016/j.chroma.2012.08.041 |
| [17] | Fu SP, Wang LX, Zhang F, et al. Determination of ligustrazin and ferulic acid in Si-wu-tang and its related preparations by capillary zone electrophoresis[J]. Chin J Chromatogr (色谱), 2003, 21: 371–374. |
| [18] | Spiro M, Page CM. The kinetics and mechanism of caffeine infusion from coffee:hydrodynamic aspects[J]. J Sci Food Agr, 1984, 35: 925–930. DOI:10.1002/(ISSN)1097-0010 |
| [19] | Spiro M, Jaganyi D. Kinetics and equilibria of tea infusion, Part 15. Transport of caffeine across a teabag membrane in a modified rotating diffusion cell[J]. Food Chem, 2000, 69: 119–124. DOI:10.1016/S0308-8146(99)00251-4 |
| [20] | Spiro M, Chong YY. The kinetics and mechanism of caffeine infusion from coffee:the temperature variation of the hindrance factor[J]. J Sci Food Agr, 1997, 74: 416–420. DOI:10.1002/(ISSN)1097-0010 |
| [21] | Chu MQ, Liu GJ. Kinetic model for extraction process of Chinese traditional medicine[J]. Acta Pharm Sin (药学学报), 2002, 37: 559–562. |
| [22] | He FY, Deng KW, Luo JY, et al. Fundamentally study on mathematical kinetic model of component extraction from FTCM[J]. China J Chin Mater Med (中国中药杂志), 2007, 32: 490–495. |
| [23] | Wang BC, Su H, Yang X, et al. Kinetic models for extraction process of natural products[J]. Chin Tradit Patent Med (中成药), 2012, 34: 2309–2312. |
| [24] | He FY, Deng KW, Wu DZ, et al. Extraction kineticai deviations of berberine alkaloids in Rhizoma Coptidis and Zuojin Formulae[J]. Chin Tradit Patent Med (中成药), 2009, 31: 1354–1359. |
| [25] | Yuan ST, Du HY, Xia K. The effect of Chinese herbal compound decoction on the dissolution effect[J]. Chin J Inform TCM (中国中医药信息杂志), 1999, 6: 29–32. |
| [26] | Tang ZS, Guo LW. Establishment of scientific principles on evaluation system for compound Chinese materia medica extraction and separation[J]. Chin Tradit Herb Drugs (中草药), 2010, 41: 841–845. |
| [27] | Su H, Wang BC, Liu WQ, et al. Kinetic mathematical models for extraction process of natural medicines[J]. Chin Tradit Herb Drugs (中草药), 2011, 42: 384–391. |
| [28] | Luo GA, Wang YM, Liang QL, et al. Chinese Medicine Systems Biology (中医药系统生物学)[M]. Beijing: Science Press, 2011. |
| [29] | Chou TC. Theoretical basis, experimental design, and computerized simulation of synergism and antagonism in drug combination studies[J]. Pharmacol Rev, 2006, 58: 621–681. DOI:10.1124/pr.58.3.10 |
| [30] | Chou TC, Martin N. CompuSyn for drug combinations PC software and user's guide: a computer program for quantitation of synergism and antagonism in drug combinations, andthe determination of IC50 and ED50 and LD50 values[J/OL]. Paramus: ComboSyn, 2005. |
| [31] | Long F, Yang H, Xu YM, et al. A strategy for the identification of combinatorial bioactive compounds contributing to the holistic effect of herbal medicines[J]. Sci Rep, 2015, 5: 12361. DOI:10.1038/srep12361 |
| [32] | Lam W, Jiang ZL, Guan FL, et al. PHY906 (KD018), an adjuvant based on a 1800-year-old Chinese medicine, enhanced the anti-tumor activity of sorafenib by changing the tumor microenvironment[J]. Sci Rep, 2015, 5: 9384. DOI:10.1038/srep09384 |
| [33] | Gong P, Cui N, Wu L, et al. Chemicalome and metabolome matching approach to elucidating biological metabolic networks of complex mixtures[J]. Anal Chem, 2012, 84: 2995–3002. DOI:10.1021/ac3002353 |
| [34] | Chen HX, Cui FX, Li H, et al. Metabolic changes during the pu-erh tea pile-fermentation revealed by a liquid chromatography tandem mass-spectrometry-based metabolomics approach[J]. J Food Sci, 2013, 78: C1665–C1672. DOI:10.1111/1750-3841.12288 |
| [35] | Yan R, Yang Y, Chen YJ. Pharmacokinetics of Chinese medicines:strategies and perspectives[J]. Chin Med, 2018, 13: 24. DOI:10.1186/s13020-018-0183-z |
| [36] | Li C. Multi-compound pharmacokinetic research on Chinese herbal medicines:approach and methodology[J]. China J Chin Mater Med (中国中药杂志), 2017, 42: 607–617. |
 2019, Vol. 54
2019, Vol. 54


