分析方法验证的目的在于确保所采用的方法或测定法能够得到准确可靠的测定结果,多国药典附录对于分析方法的验证有各自的指导原则,内容基本一致,如USP通则 < 1225 > 中对于分析方法验证的定义:在实验室研究中,分析方法的诸性能特性能够达到预期测试用途的要求的过程。
2002年,FDA开始了一项名为“21世纪药品质量”的计划,2004年发表了“21世纪药品cGMP:基于风险的方法”报告,鼓励实施现代的、基于风险的药品质量评价体系。上述计划公布了一系列目标,包括确保监管审评、合规和检查政策继续支持药品行业的持续改进和创新。随后,2011年,FDA发布了名为“过程验证:通用原则与实践”的指导原则[1],该指导原则与ICH的系列指导原则[2-4]相呼应,提倡分析方法生命周期的概念,这些指导原则对于制药行业的质量源于控制理念以及分析方法验证提出了新的要求和方向。2012年,USP验证和确认专家委员会(Validation and Verification Expert Panel)强调了分析目标特征(analytical target profile,ATP)的重要性,以获取更多以及更完整的信息,对于分析方法的变异以及方法应用于日常检验和监测过程,达到增强分析方法控制性和可靠性的目的[5]。近几年,USP对于分析方法的验证提出了新的思路和要求,发表了系列指导原则包括药典论坛中 < 1200 > —药典方法验证要求[7],和 < 1210 > —过程验证的统计学工具[8]。这些指导原则系统地描述了用以评估分析方法验证数据的原则,并提供了详细的应用于方法验证中的统计学原理和实验设计。
本文以美国药典论坛刊登的拟收载通则 < 1200 > ,< 1210 > 和USP已经收载的 < 1225 > 指导原则为基础,以《中华人民共和国药典》2015年版二部赖诺普利含量测定项下方法(Ⅰ类分析方法)为研究对象[9],应用统计学方法对赖诺普利原料药的含量测定方法进行了分析评价。采用美国药典论坛刊登的通则 < 1200 > 中的联合准确度、精密度及范围研究(precision-accuracy and range)实验设计,考察了50%、75%、100%、125%和150%共5个水平的线性范围,同时考察各浓度的准确度和精密度,用T分布统计量(T-distribution)计算各浓度通过可接受标准的概率,以评估该测定法是否通过验证。本文采用的统计学试验设计同时考察含量测定方法验证的准确度、精密度和范围,对于含量测定分析方法的关键性能参数进行综合评价和考察,因而更为系统地对于含量测定分析方法进行总体评估。结果表明,该方法采用的评价体系能够对Ⅰ类分析方法的准确度与精密度进行兼顾考虑,确保方法以较高的概率,具备所需要的准确度和精密度。该研究符合分析目标特征和决策准则(decision rules,DR)的理念,并与风险控制和科学公正检验的理念相一致。
1 含量测定方法选择 1.1 含量测定方法[9] 1.1.1 仪器与试剂Waters e2695液相色谱仪(配有2998PDA检测器),Mettler Toledo XP205电子天平,MilliQ纯水仪。
乙腈为色谱纯,磷酸二氢钠、氢氧化钠、2-氨基-4-苯基丁酸为分析纯,赖诺普利对照品购自中国食品药品检定研究院(批号100814-201202)。
1.1.2 色谱条件与系统适用性试验采用十八烷基硅烷键合硅胶色谱柱(Shiseido Capcell Pak C18 AQ,250 mm×4.6 mm,5 μm),以磷酸盐缓冲液(0.02 mol·L-1磷酸二氢钠溶液,用氢氧化钠试液调节pH至5.0)-乙腈(92:8)为流动相,流速1.0 mL·min-1,检测波长215 nm,柱温50 ℃。取赖诺普利对照品与2-氨基-4-苯基丁酸适量,加水溶解并定量稀释制成每1 mL中分别含1 mg与0.01 mg的混合溶液,取20 μL,注入液相色谱仪,赖诺普利峰与2-氨基-4-苯基丁酸峰的分离度应符合要求,理论板数按赖诺普利峰计算不低于700。赖诺普利对照品典型色谱图见图 1。

|
图 1 赖诺普利对照品典型色谱图 Figure 1 Representative chromatogram of lisinopril reference standard |
精密称取赖诺普利对照品约20 mg,加水溶解并定量稀释至100 mL,即得供试品溶液,精密量取20 μL,注入液相色谱仪,记录色谱图。
1.2 统计学模型本文采用经典最小二乘线性模型[10],假设方差为正态独立同分布(independent and identically distributed),模型表示为
| ${Y_\mathit{i}} = \mathit{\alpha + \beta }{\mathit{X}_\mathit{i}} + {e_\mathit{i}}, {\rm{\;\;}}\mathit{i = }{\rm{1}}\mathit{, } \cdots \mathit{, n} $ |
其中α为Y轴的截距,代表当标准物质浓度为0时的响应值;β为拟合直线的斜率,代表单位标准物质改变引起的响应改变;ei为观察值Yi的随机误差,假定ei为独立同分布,服从标准正态分布N(0,σ2)。
在误差正态分布假设下:
| $\begin{array}{l} E\left( {{Y_\mathit{i}}} \right) = \alpha + \mathit{\beta }{\mathit{X}_\mathit{i}}\\ {\mathop{\rm var}} \left( {{Y_\mathit{i}}} \right) = {\mathit{\sigma }^2} \end{array} $ |
采用最小二乘方法对浓度以及响应值进行回归,定义a和b为α和β的估计,则回归直线可以表示为
| ${\mathit{\hat Y}_\mathit{i}} = \mathit{\hat \alpha } + \mathit{\hat \beta }{\mathit{X}_\mathit{i}} $ |
即
| $\begin{array}{l} {\mathit{S}_{XX}} = \sum\limits_{i = 1}^n {{{\left( {{\mathit{X}_\mathit{i}} - \overline X } \right)}^2}} \\ {S_{XY}} = \sum\limits_{i = 1}^n {\left( {{X_i} - \overline X } \right)\left( {{Y_\mathit{i}} - \overline Y } \right)} \\ {S_{YY}} = \sum\limits_{i = 1}^n {{{\left( {{Y_\mathit{i}} - \overline Y } \right)}^2}} \end{array} $ |
则有:
| $\begin{array}{l} a = \overline Y - b\overline X \\ b = \frac{{{S_{XY}}}}{{{S_{XX}}}}\\ {{\mathit{\hat \sigma }}^2} = \frac{1}{{n - 2}}\sum\limits_{i = 1}^n {{{\left( {{Y_\mathit{i}} - a - b{X_\mathit{i}}} \right)}^2}} \end{array} $ |
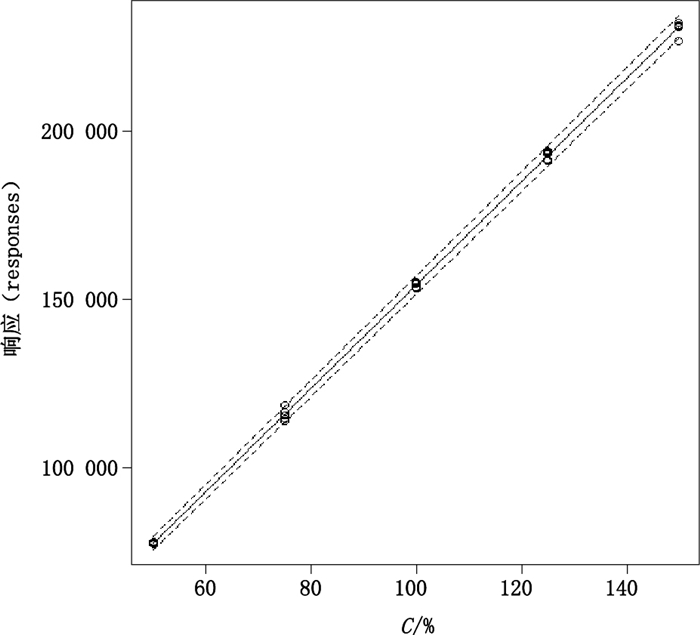
表 1为含量测定方法所采用的溶液百分浓度与色谱响应及RSD数据;拟合曲线参数、95%置信区间估计及显著性检验结果见表 2。图 2为拟合的标准曲线、95%置信区间及显著性检验结果。采用最小二乘拟合的最终模型为Y=979.5+1 534.9X,截距a的95%置信区间为(-441.6~2 400.6),该置信区间包含0,且其P值为0.169 > 0.05,说明在5%显著水平上,不能拒绝原假设(H0:a=0),因此,可以认为当标准物质浓度为0时,95%的置信水平上,响应值与0并没有统计学意义上的显著性差异。斜率b的95%置信区间为1 521.5~1 548.3,该置信区间不包含0,其P值< 2×10-16,表示在0.1%显著水平上,拒绝原假设(H0:b=0),即浓度的变化显著引起响应的变化(见表 2)。
|
图 2 拟合直线 Figure 2 The fitted line |
|
|
表 1 含量测定方法所采用的百分浓度与色谱响应数据 Table 1 Concentration in percentage and chromatographic response |
|
|
表 2 拟合曲线参数、95%置信区间估计及显著性检验结果 Table 2 Parameters of the fitted model, 95% confidence interval and results of significant hypothesis test |
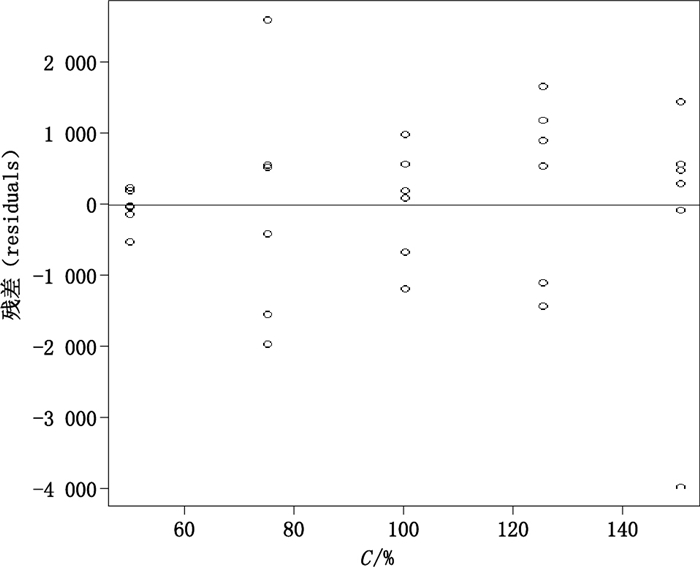
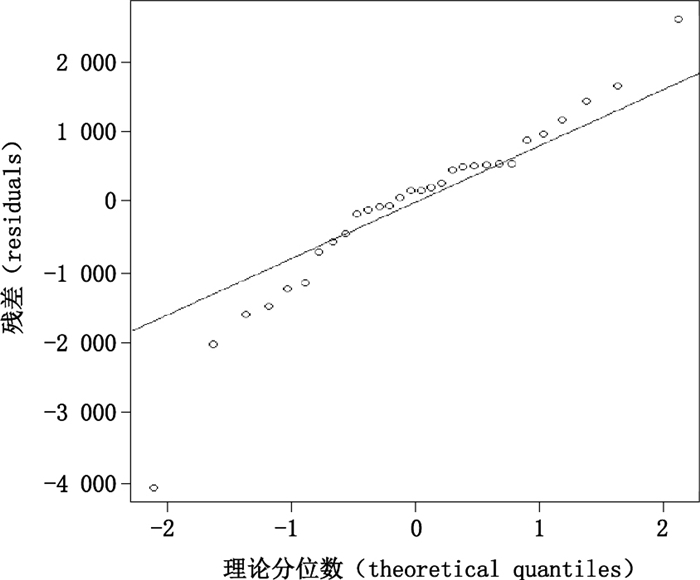
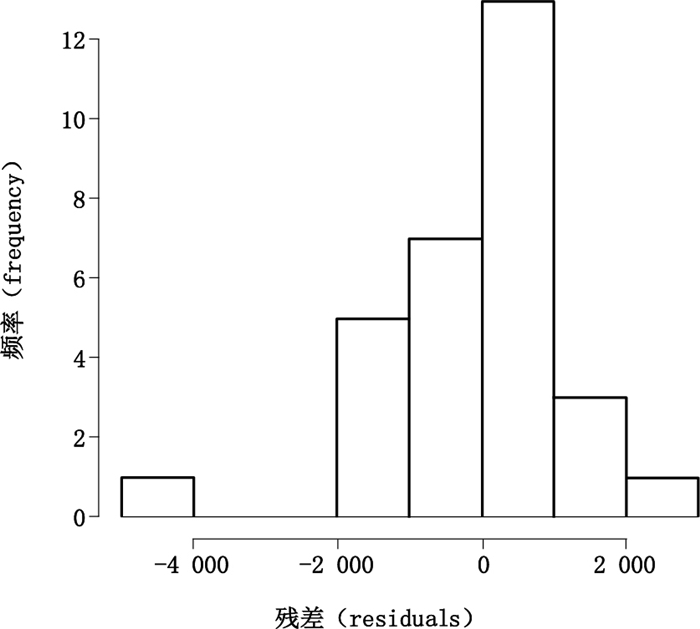
图 3为残差对于浓度的示意图,图 4、5为残差的QQplot示意图和直方图。由图 3可见,各浓度点的残差分散于直线Y=0的两侧,QQplot图及直方图说明残差呈现接近正态分布,说明在重复性条件下,在50%~150%范围内,残差呈现相同的分布,因此该方法的精密度可采用合并标准差的方式进行描述。标示浓度为50%、75%、100%、125%和150%,在重复性条件下的RSD分别为0.36%、1.4%、0.52%、0.66%、0.83%,合并RSD为7.6%,小于USP < 1200 > 中对于重复性标准差的要求1%,因此方法的线性和范围通过验证。如果在测定结果出现明显的异常值,则可通过适当的异常值检测方法,并回顾试验过程,调查出现异常值的原因后,剔除异常值。
|
图 3 残差对于浓度的示意图 Figure 3 Residuals vs. concentrations |
|
图 4 残差的QQplot示意图 Figure 4 QQplot for residuals |
|
图 5 残差的直方图 Figure 5 Histogram for residuals |
USP General Chapter < 1200 > 中采用T分布对于测试结果的概率进行计算和评价。构造t统计量:
| $\begin{array}{l} E{\rm{ = }}\left( {x - \overline x } \right) = 0, \\ {\mathop{\rm var}} \left( {x - \overline x } \right) = {S^2}\left( {1 + \frac{\mathit{1}}{n}} \right)\\ {\rm{SE}}\left( {\mathit{x - }\mathit{\overline x} } \right) = S\sqrt {1 + \frac{\mathit{1}}{n}} \end{array} $ |
| $\begin{array}{l} {\mathit{q}_{\rm{U}}} = \frac{{\left( {{\rm{Upper - Mean}}} \right)}}{{\left( {{\rm{SD}}\sqrt {1 + \frac{\mathit{1}}{n}} } \right)}}\\ {q_{\rm{L}}} = \frac{{\left( {{\rm{Lower - Mean}}} \right)}}{{\left( {{\rm{SD}}\sqrt {1 + \frac{\mathit{1}}{\mathit{n}}} } \right)}}\\ {\rm{df = }}\mathit{n}{\rm{ - 1}}\\ {\rm{Result = }}\mathit{t}\left( {{\mathit{q}_{\rm{U}}}, {\rm{df}}} \right) - \mathit{t}\left( {{q_{\rm{L}}}, df} \right) \end{array} $ |
其中,Upper为标准上限,Lower为标准下限,SD为样品RSD,n为平行制备样品数量,df为自由度,t(q,df)是指自由度为df,分位数为q的T分布累积分布概率值,接受限度为不小于0.95。
假设采用该标准曲线测试未知赖诺普利原料药样品,含量测定项限度为98.0%~102.0%。每个待测样品平行制备6份供试品溶液,表 3为含量测定结果的均值分别为98.5%、99.0%、99.5%、100.0%、100.5%、101.0%、101.5%,RSD分别为0.2%、0.3%、0.4%、0.5%、0.6%、0.7%、0.8%的样品的概率值。
|
|
表 3 含量测定结果概率表 Table 3 Probability for assay result |
由表 3中数据可见:对于平行制备6份供试品溶液,其自由度df=5,结果能否满足概率不小于95%的接受限度,取决于其均值和RSD。当均值为固定值时,RSD越小显示方法的精密度越优,则通过接受限度的概率越大,随着RSD的增大,通过接受限度的概率值减小;当RSD为固定值时,结果均值越接近100%,其概率越大。对于均值为100.0%的样品,当RSD > 0.5时,通过接受限度的概率值下降,小于95%的接受限度,表明所采用的方法精密度较差,不能满足分析需要。均值距离100%越远,对于方法精密度RSD的要求越高。当均值为98.5%,RSD=0.2%时,其概率值仍无法达到95%的接受限度,提示该方法对于分析该产品具有较大的超出质量标准(out of specification,OOS)的风险。
3 讨论通常在药物监管实验室(regulatory laboratory)中,对于1个分析方法或测定法准确度的评价是通过测定结果的均值与真实值之间的偏差(回收率)或采用标准曲线法进行,精密度的评价通过对实验结果的RSD进行。对于方法通过验证通常采用经验的标准,如《中华人民共和国药典》中规定,方法回收率在98%~102%之间,方法重复性RSD不得超过1%,方法重现性不得超过2%。
本文所采用美国药典论坛刊登的通则 < 1200 > 中的联合准确度、精密度及范围研究(precision-accuracy and range)实验设计,兼顾了对于准确度、精密度、线性和范围的评价。准确度方面,以T分布为基础,以样品测定结果-均值作为样品准确性的评价参数,计算出在《中华人民共和国药典》规定的限度(98%~102%)内该实验结果接受限度的概率,接受标准为不小于95%。线性和范围方面,考察了对照品溶液浓度50%、75%、100%、125%和150%共5个水平的线性范围,并对拟合标准曲线的斜率和截距进行了检验,对残差的正态性进行了考察。结果表明,该方法能完全满足其对质量标准限度在90%~110%范围内检品的检测要求。
该方法从统计学的角度,通过兼顾准确度、精密度和线性的实验设计,以确保测定法所得到的结果具有较高的概率通过标准中所规定的接受限度。该方法采用的评价体系,能够对第Ⅰ类分析方法的准确度与精密度进行兼顾考虑,确保方法以较高的概率,保证检测结果的可靠性。该研究符合分析目标特征(analytical target profile,ATP)和决策准则(decision rules,DR)的理念,并与风险控制和科学公正检验的理念相一致。
| [1] |
FDA. Guidance for Industry-Process Validation: General Principles and Practices[S]. 2011
|
| [2] |
ICH Secretariat. ICH Harmonized Tripartite Guideline: Pharmaceutical Development Q8(R2)[S]. 2009
|
| [3] |
ICH Secretariat. ICH Harmonized Tripartite Guideline: Quality Risk Management Q9[S]. 2005
|
| [4] |
ICH Secretariat. ICH Harmonized Tripartite Guideline: Pharmaceutical Quality System Q10[S]. 2008
|
| [5] |
MARTIN GP, KIMBER LB, CHRISTOPHER B, et al. Stimuli to the revision process: lifecycle management of analytical procedures: method development, procedure performance qualification, and procedure performance verification[J/OL]. Pharmacopeial Forum, 39(5)[2017-10-15]. http://www.usp.org/uspnf/notices/stimuli-article-lifecyclemanagement-analytical proceduresposted-comment
|
| [6] |
USP 40-NF 35 General Chapter <1225>Validation of Compendial Procedure[S]. 2017: 1780
|
| [7] |
USP in Process Revision <1200>. Requirements for Compendial Validation[J/OL]. Pharmacopeial Forum, 2013, 39(6)[2017-10-15]. http://www.usppf.com/pf/pub/index.html
|
| [8] |
USP in Process Revision <1210>. Statistical Tools for Procedure Validation[J/OL]. Pharmacopeial Forum, 2014, 40(5)[2017-10-15]. http://www.usppf.com/pf/pub/index.html.
|
| [9] |
中华人民共和国药典2015年版.二部[S]. 2015: 1457 ChP 2015. Vol Ⅱ[S]. 2015: 1457
|
| [10] |
CHOW SC. Statistical Design and Analysis in Pharmaceutical Science:Validation, Process Controls, and Stability[M]. New York: Marcel Dekker, Inc, 2002: 31.
|
 2019, Vol. 39
2019, Vol. 39 
