国家教育部主管、北京师范大学主办。
文章信息
- 刘畅, 伍新春. 2017.
- LIU Chang, WU Xinchun. 2017.
- 主客体互倚性的成对模式及其检验
- Dyadic Patterns in the Actor-Partner Interdependence Model and its Testing
- 心理发展与教育, 33(1): 105-112
- Psychological Development and Education, 33(1): 105-112.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2017.01.12
2. 北京师范大学心理学院, 应用实验心理北京市重点实验室, 北京 100875
2. School of Psychology, Beijing Key Laboratory of Applied Experimental Psychology, Beijing Normal University, Beijing 100875
成对关系是人际互动和人际关系的基本单元 (Kenny, Kashy, & Cook, 2006)。我国传统的“五伦”界定涵盖了五种常见的成对关系类型,即夫妻关系、亲子关系、兄弟关系、上下级关系和朋友关系 (李育辉, 黄飞, 2010)。成对关系的互倚性是关系的重要特点,这一特点导致了成对关系中的个体提供的数据的非独立性 (non-independence),即如果成对关系中两个成员的两组数据是非独立的,那么这两组数据比非成对关系中两个个体的两组数据更具有相似性 (或差异性)(Kenny et al., 2006)。数据的非独立性导致两个个体的观测变量存在相关,即其中一个个体得分的信息提供了另一个体得分的信息 (Cook & Kenny, 2005)。主客体互倚性模型 (Actor-Partner Interdependence Model, Cook & Kenny, 2005),简称APIM,国内也有学者称之为行动者-对象互依性模型,它考虑了成对数据的非独立性,是婚姻、家庭等研究领域中成对数据分析的新兴方法,为成对关系的解读提供了有效的手段。
基于互倚理论,Kenny等人论述了APIM的四种普遍模式 (pattern):主体模式 (actor-oriented)、客体模式 (partner-oriented)、对偶模式 (couple-oriented) 与社会比较模式 (social comparison)(Kenny & Cook, 1999)。但由于缺乏系统的统计方法,此后APIM的成对模式研究仅限于定性的推论。Kenny等人之后采用对比模式 (contrast pattern) 代替了社会比较模式,保留了主体模式 (actor-only)、客体模式 (partner-only) 和对偶模式 (couple pattern) 的提法,并提出了检验四种成对模式的方法 (Kenny & Ledermann, 2010),为后续研究中评估与比较APIM的四种成对模式提供了定量的分析方法。
1 APIM标准模型及其成对模式 1.1 APIM的提出如果在处理成对数据时,将成对关系中的个体数据合成总分或平均分来分析关系水平的影响,则无法得到关系中的个体信息。以婚姻满意度为例:在夫妻双方中,一方婚姻满意度较高,另一方婚姻满意度较低,二者的合成分与夫妻双方都感受到中等程度的婚姻满意度的合成分就会相等,从而忽视了这两种夫妻关系之间的个体差异 (Cook & Kenny, 2005)。如果在成对关系中,忽略数据的非独立性而使用个体数据作为分析单元,则会增大统计检验时犯Ⅰ类和Ⅱ类错误的可能性 (Kenny et al., 2006)。APIM以成对数据而非个体数据作为分析单元,分析的样本容量是成对关系的数量而非被试个体数量 (Kenny et al., 2006),将个体测量结果嵌套于成对关系中进行处理 (Cook & Kenny, 2005),从而有效地解决了成对数据分析时非独立的数据检验。
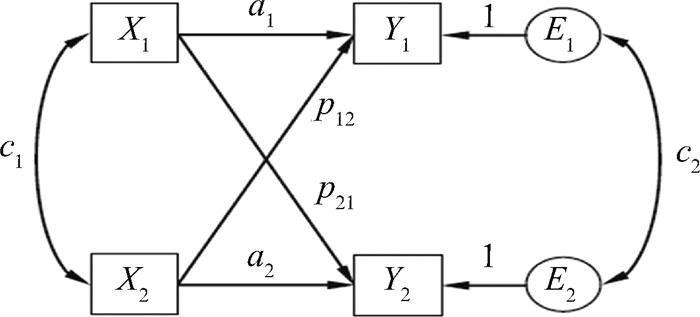
APIM的标准模型 (Cook & Kenny, 2005; Kenny & Ledermann, 2010) 包括4个变量 (见图 1):Y1与Y2分别为个体A与个体B的因变量,X1与X2分别为个体A与个体B对Y的预测变量。a1与a2分别代表的是个体A与个体B的主体效应 (actor effect),即个体对自身结果变量的影响;p21是个体A对个体B的客体效应 (partner effect),p12是个体B对个体A的客体效应,即个体对成对关系中对方结果变量的影响,客体效应反映的就是成对关系中的互倚性。
|
| 图 1 APIM标准模型 (资料来源:Kenny & Ledermann, 2010) |
该模型在预测变量与因变量之间设置预测路径的同时,在预测变量之间及因变量的残差项之间也设相关,即c1与c2。c1是两个自变量之间的相关,设置这个相关的目的是在任一X变量预测Y变量时,控制另一X变量的影响。因此,主体效应是在控制了客体效应基础上评估的,客体效应也是在控制了主体效应基础上评估的。c2是Y变量未被X变量所解释的残差项之间的相关,设置这个相关是为了控制互倚性的其他来源。如果预测变量是Y1与Y2相关的唯一原因 (例如互倚性的唯一来源),当Y1与Y2由预测变量产生的变异剔除后,Y1与Y2就不再相关了。但实际情况中,Y1与Y2可能由其他原因造成相关,例如个体A与B来自于同一个家庭,在研究所考虑的预测变量外,其他未测量的共同原因如家庭功能,也可能造成Y1与Y2相关。c2就是Y1与Y2相关中未被解释的变异 (Cook & Kenny, 2005; Kenny & Ledermann, 2010)。
APIM的标准模型为饱和模型,模型恰好识别 (just-identified),APIM可以通过混合回归法 (pooled-regression method)、多水平模型 (multilevel modeling)、结构方程模型 (structural equation modeling) 等方法进行分析 (Kenny et al., 2006; Kenny & Ledermann, 2010)。
1.2 APIM的成对模式主体效应与客体效应在原则上是相互独立的 (Kenny et al., 2006),研究者需要考虑的是在某一特定情境下,哪种过程在起作用 (Kenny & Cook, 1999)。Kenny等人在APIM框架下同时考虑主体效应与客体效应时,所提出的四种模式,即主体模式、客体模式、对偶模式与对比模式 (Kenny & Cook, 1999; Kenny & Ledermann, 2010) 在关系研究中,特别是在夫妻关系研究中具有重要的意义 (Kenny et al., 2006)。
对于成对关系中的个体而言,主体模式指主体效应非零,客体效应为零,即个体的预测变量对自身的结果变量有影响,但不能作用于对方的结果变量 (a不等于0,p等于0);客体模式指客体效应非零,主体效应为零 (a等于0,p不等于0),这种模型在研究中非常少见;对偶模式指主体效应与客体效应相等且作用效果相同 (不存在显著差异),即个体的结果变量同等地受自身预测变量及关系中另一方的预测变量的影响 (a等于p);对比模式指主体效应与客体效应的绝对值相等但符号 (作用) 相反 (a加p等于0),例如个体的结果变量受自身预测变量的正向预测作用,受另一方预测变量的负向预测作用 (Kenny & Cook, 1999; Kenny et al., 2006; Kenny & Ledermann, 2010)。
不同的成对模式提示了成对关系中的不同过程 (Kenny & Ledermann, 2010):如果在成对关系中,自我与他人的界限不清,就会发现对偶模式。对偶模式提示了个体与关系中另一方的预测变量同等地影响个体的结果变量。如果不存在成对作用,就可能会发现主体模式,起作用的预测变量是个体自身的预测变量。对比模式则提示了另一种成对作用的存在,而这种作用是补偿的 (你做得越多,我需要做得就越少) 或竞争的 (我要做得比你多)。此时,起作用的预测变量则是个体的预测变量减去关系中另一方的预测变量。客体模式在研究中很少见,如果研究者关注的是个体特征对关系中另一方的影响,例如个体的外表魅力对成对关系中另一方的关系满意度的影响时,就可能发现客体模式。
研究者在家庭研究、群体研究等领域的研究中证实了不同成对模式的存在。例如Ponnet等人在父母的教养压力、婚姻关系与其教养风格的关系研究中发现,父母的教养压力与教养风格的成对模式是主体模式,而父母的婚姻关系与教养风格的成对模式则是客体模式 (Ponnet et al., 2013)。也就是说,父母的教养风格受自身感受到的教养压力及配偶感受到的婚姻关系的影响,父母自身感受到的婚姻关系则对其教养风格是没有作用的。
2 APIM成对模式的检验在APIM中,如果只检验主体效应和客体效应的显著性从而推出模型为主体模式、客体模式、对偶模式或对比模式的结论比较危险。比如研究者可能发现主体效应或客体效应是显著的,从而认为是主体模式或客体模式,但该模式其实可能应为对偶模式;比较极端的现象是,主体效应与客体效应都是不显著的,但APIM的模式仍可能为对偶模式 (Kenny & Ledermann, 2010)。因此,Kenny等人提出了对APIM的模式进行检验的方法,并将其中涉及的检验参数命名为k以表示对成对关系研究先驱Larry Kurdek的敬意 (Kenny & Ledermann, 2010)。
2.1 k值的含义由于客体模式在研究中非常少见,因此Kenny等人在不考虑该模式的基础上提出了对APIM的成对模式进行检验的方法,即通过客体效应与主体效应的比值k来判断APIM的成对模式 (Kenny & Ledermann, 2010)。根据k值的定义,首先主体效应应该是非零的,以避免除数为零。这里的基础假设是主体效应是相对重要的。如果a较小,那么k的估计将会非常不稳定。因此,首先要估计饱和模型,考察主体效应的大小。尽管很难确定一个通常的值,但Kenny等人建议,如果标准化的主体效应的绝对值小于0.10,就不应该计算k值 (Kenny & Ledermann, 2010)。
k值作为客体效应与主体效应的比值,其理论取值从负无穷到正无穷。但k值的三个取值对于家庭研究具有重要意义,即0,1和-1。如果是主体模式,则k值等于0;如果是对偶模式,则k值等于1;如果是对比模式,则k值等于-1。如果k值取值为0.5,那么说明主体效应是客体效应的2倍,APIM的模式介于对偶模式和主体模式之间 (Kenny & Ledermann, 2010),这种模式可称为混合模式。
2.2 k值的估计与成对模式检验在计算k值对成对模式进行检验之前,首先要确定分析的成对关系是可区分的成对关系还是不可区分的成对关系。所谓可区分的成对关系,指关系中的两个个体可通过他们的角色 (如母亲与孩子) 或其他特征 (如兄弟姐妹的出生顺序) 进行区分;不可区分的成对关系,指关系中的两个个体无法区分 (如双胞胎不能按年龄将其区分、同性夫妻无法按性别将其区分)(Cook & Kenny, 2005)。不可区分的成对关系也称为可交换的关系,即没有系统的或有意义的变量将成对关系中的个体进行区分;如果将成对关系看作是可区分的,则说明存在有意义的变量来组织关系中的个体数据 (如年龄、性别等)(Kenny et al., 2006)。
在研究中,即使可应用角色或其他特征将成对关系进行区分 (如父母),也应注意在特定的研究中,双方的主体效应与客体效应也可能是不可区分的。因此,Kenny等人建议,同时限制双方数据的主体效应相等、客体效应相等,考察模型的卡方值变化是否显著,如果没有差异,则将其作为不可区分的成对数据进行分析,如果存在差异,则视为可区分的成对数据;检验时采用较为宽松的显著性水平,比如0.20 (Kenny & Ledermann, 2010)。例如在一项酗酒研究中,研究者考查了浪漫关系中酗酒的个体间的影响 (Mushquash et al., 2013)。在该研究中,成对关系是可以根据男性与女性进行区分的,因此为可区分的成对关系。研究者在计算k值之前,首先限制了男性与女性的效应相等,结果发现限制模型与无限制模型不存在显著差异,因此在后续的成对模式分析中,按照不可区分的成对数据进行检验。
需要注意的是,在限制效应相等时,比较的是非标准化系数而不是标准化系数。在考察效应是否相等时,待检验的零假设是个体A与个体B的回归系数相等。考察是否男性比女性在X对Y的作用上更大时,研究者想知道的是如果男性的X增加一个单位,是否比女性的X增加一个单位,能够引起更多的Y的变化,这是非标准化回归系数评估的差异。如果在两个群体内进行标准化,就会失去度量等价性,此时检验的就不再是零假设 (Kenny & Ledermann, 2010)。
此外,由于k值是比值,其分布可能偏态,违反正态性假设,因此计算其bootstrap置信区间而非标准误更为合理 (Kenny & Ledermann, 2010)。如果bootstrap无法应用时,也可通过估计k值的标准误 (Kenny & Ledermann, 2010) 来估计k值的置信区间。采用一阶delta法 (first order delta method),k值 (k=p/a) 的标准误为:
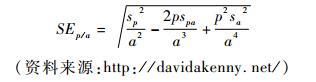
|
其中,a为非标准化的主体效应;p为非标准化的客体效应;Sa2为主体效应的方差 (标准误的平方);Sp2为客体效应的方差 (标准误的平方);Spa为主体效应与客体效应的协方差。
2.2.1 k值的分析程序在多水平模型中,k值可通过客体效应与主体效应的比值间接地计算出来,Kenny等人在《成对数据分析》一书 (Kenny et al., 2006) 中讨论了通过多水平模型对对偶模式与对比模式的评估,但标准的多水平模型中无法直接估计k值及其置信区间。在Stata软件中,xtmixed程序可用于估计APIM,采用nlcom功能可计算k值及其bootstrap置信区间。根据Kenny等人介绍的方法 (Kenny & Ledermann, 2010),采用结构方程模型可在结果中直接输出k值的取值及其boostrap置信区间,相较而言更为直接、有效。下面具体说明如何采用结构方程模型计算k值。
2.2.2 k值的计算与成对模式检验 2.2.2.1 可区分成对关系的k值计算与成对模式检验在可区分的成对关系中,存在两个k值,成对关系中的两个个体都可估计出一个k值 (Kenny & Ledermann, 2010),即:
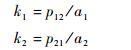
|
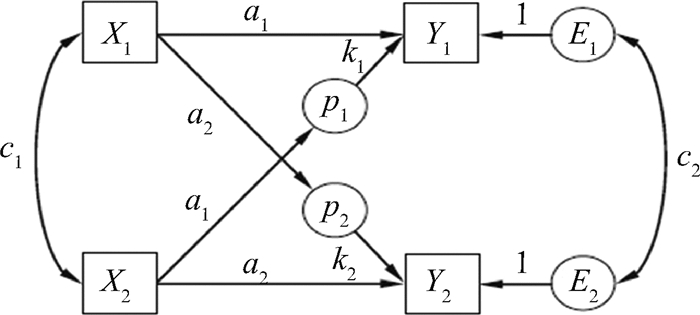
其中,k1为个体A的值,k2为个体B的值。在结构方程模型中,k值可通过在模型中设置幽灵变量 (phantom variables) 直接进行估计 (Kenny & Ledermann, 2010)。设置的幽灵变量为潜变量,没有实质意义也不会对模型造成干扰;这类变量作为结构方程中的辅助变量,可在因子载荷和结构参数中进行多样化的限制 (Rindskopf, 1984)。幽灵变量的引入不影响参数估计及方差、协方差,因此不会影响结构方程模型的拟合指数。如图 2所示,通过在两个客体效应的路径中设置幽灵变量P1与P2,可在APIM中直接估计k1与k2。X2对Y1的预测,是通过P1的“中介”作用实现的。X2对P1的效应固定为a1(X1对Y1的主体效应),P1到Y1的估计为k1。因为k1=p12/a1,所以X2对Y1的“直接效应”为a1k1,即p12。同样地,P2中介X1到Y2的预测作用,P2到Y2的估计为k2。因为k2=p21/a2,所以X1对Y2的“直接效应”为a2k2,即p21。虽然加入了幽灵变量,但图 1和图 2是统计相等模型,图 2的模型也是饱和模型 (Kenny & Ledermann, 2010)。
|
| 图 2 加入幽灵变量的APIM标准模型 (资料来源:Kenny & Ledermann, 2010) |
通过设置幽灵变量,可得到k1与k2的取值,再分别计算k1与k2的bootstrap置信区间,评估是否有0,1或-1在置信区间内 (Kenny & Ledermann, 2010):如果1在置信区间,而0和-1不在,就限制k等于1重新对模型进行估计,此时模型是过度识别 (overidentified),可以判断模型是否拟合良好。如果模型拟合良好,说明k等于1时模型可以接受,则可认为模型为对偶模式;如果模型拟合明显变差,说明模型无法接受k等于1,即不支持模型为对偶模式。而如果0或者-1在置信区间内,则限制k等于0或者-1,考察模型拟合情况,如果模型拟合良好,则可认为模型为主体模式或对比模式。此外,还可进一步检验k1与k2是否相等。如果二者可以相等,那么就使用单一的k值。若此时模型的拟合比估计两个k值时拟合更好,那么就可以计算这个共同k值的bootstrap置信区间。例如,经检验k1=k2,单一k值的平均值为0.86。此时如果1在置信区间,而0不在置信区间,而且当限制k=1时,模型拟合没有变差,那么就可以认为是对偶模式。
因此,在可区分的成对关系中,Kenny等人建议遵循如下步骤进行检验:第一步,估计饱和模型 (如图 1);第二步,检验模型的两个主体效应与两个客体效应是否相等。如果主体效应及客体效应相等,则按不可区分的成对数据进行分析。如果不相等,而且两个主体效应的绝对值都大于0.10,那么就估计包含幽灵变量的APIM模型,估计两个k值;第三步,检验两个k值是否相等,如果两个k值不存在差异,就使用一个k值。最后,计算k值的置信区间,评估是否固定k值为0,1或-1(Kenny & Ledermann, 2010),如果0,1或-1在置信区间内,则固定k值为0,1或-1,检验模型拟合情况,判断模型是否支持某一成对模式。
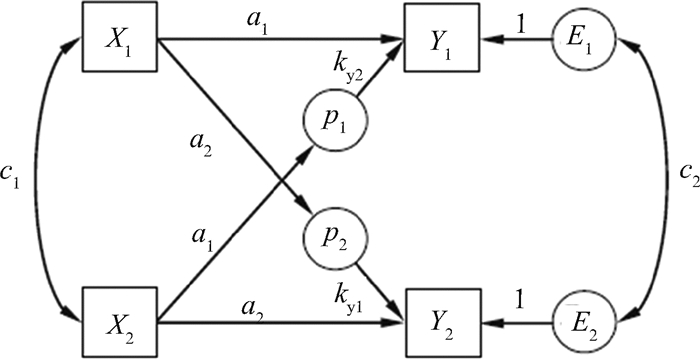
在可区分的成对关系中,可能还存在另外一种情况 (Kenny & Ledermann, 2010):之前所述的对偶模式指对于因变量Y而言,主体效应与客体效应相等 (如a1=p12);对偶模式也可从预测变量X的角度进行界定,如个体A的X1对于Y1与Y2的预测作用相等 (a1=p21),也是对偶模式的表现。Kenny等人将此时的k记为kY(Kenny & Ledermann, 2010),加入幽灵变量的APIM标准模型见图 3。kY的检验步骤与k相同,区别在于k1=p12/a1,所以X2对Y1的“直接效应”为a1 k1,即p12;而kY1=p21/a1,所以X1对Y2的“直接效应”为a1 kY1,即p21。同样,k2=p21/a2,所以X1对Y2的“直接效应”为a2k2,即p21;而kY2=p12/a2,所以X2对Y1的“直接效应”为a2 kY2,即p12。
|
| 图 3 加入幽灵变量的APIM标准模型 (kY) (资料来源:Kenny & Ledermann, 2010) |
在不可区分的成对关系中,关系中的个体是可以互换的。Olsen等人的方法可用于结构方程模型中评估不可区分成对关系的APIM (Olsen & Kenny, 2006),该方法在模型中限制6个相等:预测变量的均数和方差相等、因变量的截距相等、误差方差相等、主体效应相等、客体效应相等。限制相等后,该模型也可称为可交换的饱和 (interchangeable and saturated, ISAT) 模型。在不可区分的成对数据中,作为零模型进行比较的是ISAT模型。
在分析不可区分的成对数据时,Kenny等人建议遵循如下步骤进行检验:第一步,检验不可区分的饱和模型 (如ISAT)。第二步,如果两个主体效应的绝对值都大于0.10,估计设置幽灵变量的APIM。在设置幽灵变量的APIM中,k1=k2,该模型与之前估计的ISAT是统计相等模型。第三步,计算k值的bootstrap置信区间,判断0,1或-1是否在置信区间内。如果有,则限制k值等于0,1或-1,将此模型的卡方值与ISAT模型的卡方值进行比较,考察限制参数后模型是否仍能拟合数据 (Kenny & Ledermann, 2010)。
2.2.3 APIM成对模式的检验流程在介绍成对模式检验流程之前,首先应注意的是Kenny等人在提出k值时,是建立在客体模式在研究中较为少见的基础上。但在一些研究中,研究者可能更关注客体模式,例如个体的外表魅力对成对关系中另一方的关系满意度的影响。此时,客体效应可能会比主体效应更强,不应再使用客体效应与主体效应的比值,而是使用k的倒数k-1进行分析 (Kenny & Ledermann, 2010),如果k-1为0,那么就认为存在客体模式 (Ledermann, Macho, & Kenny, 2011)。因此,对k值进行检验之前,研究者首先要明确的是研究目的是否为检验客体模式。
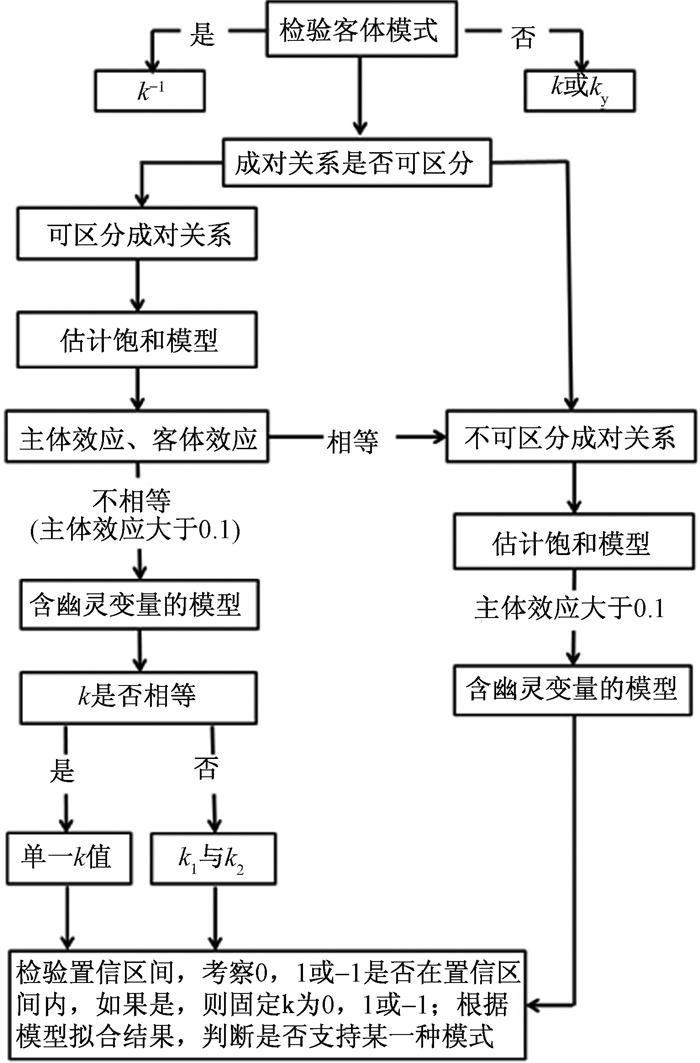
综上,根据Kenny等人对主客体互倚性的成对模式的分析方法,k值的检验流程可归纳如下 (见图 4):
|
| 图 4 k值检验流程 |
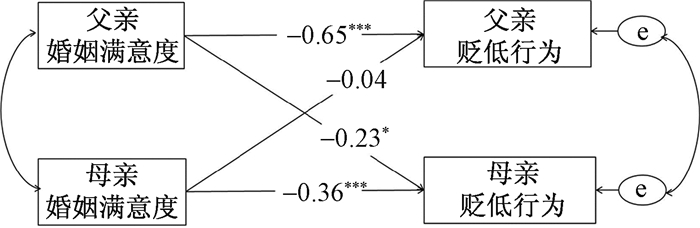
下面用一个实际例子说明如何对主客体互倚性的成对模式进行检验。本例感兴趣的是父母在婚姻关系中的情绪、情感与行为是否会迁移到与配偶共同抚养儿童的行为中,即父母的婚姻满意度与协同教养中贬低配偶行为的关系,探讨该关系中父亲或母亲是否支持某一种成对模式,模型图如图 5所示。示例研究共有317对3~7岁儿童的父母参与了问卷调查。其中,父亲平均年龄34.19±4.55岁,母亲平均年龄31.93±4.21岁;儿童的平均年龄7.59±3.53岁,男生189人,女生175人。有关变量涵义、测量工具及施测方法等具体内容可参见陈玲玲等 (陈玲玲, 伍新春, 刘畅, 2014) 的研究,本例只涉及APIM成对模式的检验,不涉及其他模型检验等问题。
|
| 图 5 k示例模型图 |
由于父亲和母亲可以根据其角色进行区分,因此首先按照可区分的成对关系检验APIM的标准模型。APIM非标准化系数的结果如图 5所示,非标准化与标准化 (括号内) 的各效应分别为:父亲的主体效应为-0.65(-0.37),母亲的主体效应为-0.36(-0.25);客体效应中,父亲对母亲的预测作用为-0.23(-0.15),母亲对父亲的预测作用为-0.04(-0.03)。标准模型为饱和模型,结果显示主体效应显著,父亲对母亲的客体效应显著,但母亲对父亲的客体效应不显著。
在计算k值之前,首先限制模型的父母主体效应、父母客体效应相等,结果发现χ2(2)=3.57,p=0.17,小于Kenny等人建议的0.20,说明模型无法接受父亲与母亲的效应相等。因此在进一步的成对模式分析中,仍将其作为可区分的成对关系进行计算。根据饱和模型结果,父亲与母亲的主体效应的标准化绝对值均大于0.1,因此可以通过估计包含幽灵变量的APIM对k值进行估计。通过bootstrap重复抽样5000次进行置信区间估计。经检验,父亲的k值等于0.07,95%置信区间从-0.19到0.40,0在置信区间内,提示了父亲的成对模式为主体模式;母亲的k值等于0.64,95%置信区间从0.13到1.52,1在置信区间内,提示了母亲的成对模式为对偶模式。
为验证父亲与母亲的成对模式,限制k等于置信区间内的特殊值 (父亲等于0,母亲等于1)。模型的卡方变化不显著,χ2(2)=0.66, p=0.72,支持了父亲是主体模式,母亲是对偶模式。虽然在限制父亲的k值与母亲的k值相等时,模型仍可以接受,χ2(1)=1.93, p=0.16,但模型要比限制父亲k值为0、母亲k值为1拟合差。因此,在婚姻满意度对父母贬低行为的影响中,父亲受自身婚姻满意度的影响,而母亲既受自身婚姻满意度又受父亲婚姻满意度的影响。
4 APIM的成对模式及k值的评价 4.1 优势虽然APIM是一种成对关系的研究方法,但目前研究中主要是分别地估计与检验主体效应与客体效应,在考虑主体效应与客体效应的相对大小方面,APIM的四种成对模式为理解成对关系的过程提供了简洁而有力的信息 (Kenny & Ledermann, 2010)。
k值为归纳主体效应与客体效应的关系提供了量化分析方法,能够检验研究是否支持与理论相关的某一模式。k值检验方法的提出,可检验成对关系中的一系列假设,通过k值的计算,研究者可以得到量化指标,而不是对主体效应和客体效应相对大小的定性描述 (Kenny & Ledermann, 2010)。k值的优势还在于,置信区间的评估可以得到k值的取值范围,如果k值是一个特殊值,则可以通过模型比较等方式验证假设;通过k值可以发现只考察主体效应或客体效应时所无法发现的有趣模式,如对偶或对比模式;在可区分的成对数据中,例如异性夫妻,同时计算男性与女性的k值,可以发现成对关系中的性别差异;此外,通过k值可在元分析中对不同的研究进行比较 (Kenny & Ledermann, 2010)。
4.2 局限性在k的分析中存在三种方式,即k,ky与k-1。如果成对关系是不可区分的,那么根据不同的理论假设,k值可以通过三个形式进行计算,导致分析方法的复杂化,也为k值在不同研究中的比较造成麻烦。同时,k值的检验程序较为繁琐,虽然结构方程模型可以直接输出k值及其置信区间,但Kenny等人建议的方法需要设置幽灵变量。如果涉及两个以上的预测变量或结果变量 (多变量情况),特别是在考虑控制变量时,检验程序及模型的设置更为复杂。
此外,在成对关系的研究中,研究者起初主要是基于理论提出了成对关系可能存在的四种普遍模式,是一种定性的描述。在引入量化分析指标之后,研究者发现了介于对偶模式与主体模式之间的混合模式。在混合模式中,主体效应大于客体效应,此时主体效应与客体效应可能都是显著的。在这种情形下,个体同时受自身与对方预测变量的影响,也可以说是对偶模式的表现,即自我与他人的界限是不清的;而Kenny等人关于对偶模式的论述更接近于对偶模式的典型表现,即主体效应与客体效应相等。因此在实证研究中,研究者可能更多地得出介于不同模式之间的混合模式,而非Kenny等人在理论上阐述的四种成对模式。
4.3 展望近年来,研究者不断地扩充主客体互倚性的成对模式的应用。例如主客体互倚性中介模型 (API mediation model or APIMeM; Ledermann et al., 2011) 与主客体互倚性群组模型 (group APIM or GAPIM; Kenny & Garcia, 2012),都可采用成对模式进行分析检验。在APIMeM (见图 6) 中,成对模式的分析能够有效地将成对数据的复杂中介关系简化;在GAPIM中,对于不同模式的分析,能够帮助研究者有效地检验某种理论或假设,得出更为简洁而概括性地结论。但Kenny等人未能对GAPIM中k值的适用性进行分析,而k值比值的特性影响了其在群体研究中的运用。由于比值具有不稳定和不对称性,在群体研究中,其他人得分由多人评定,更不易受个体偏差的影响,易于出现客体效应极大的情况 (Kivlighan Jr & Paquin, 2014)。目前已有研究采用样本校正BIC (sample-size adjusted Bayesian information criterion; SABIC)(Kenny & Garcia, 2012) 或伪R2(pseudo-R)2(Garcia, Meagher, & Kenny, 2015) 检验主客体互倚性群组模型的成对模式,未来研究可进一步探讨k值在APIM成对模式检验中的应用并探索其他可靠的检验方法。

|
| 图 6 加入幽灵变量的APIMeM标准模型 (资料来源:Ledermann, Macho, & Kenny, 2011) |
此外,研究者也在不断尝试将APIM与其他相关理论或方法进行整合。例如,Wickham和Knee从理论与方法两个方面出发,将APIM与互倚理论 (interdependence theory, IT) 进行了整合,并提出使用SAS MACRO程序对k值进行分析 (Wickham & Knee, 2012)。Kenny团队最新也编写了采用R软件分析成对数据的程序,并已经发表如何采用R软件分析GAPIM (例如,Garcia, Meagher, & Kenny, 2015)。可见,APIM的方法学研究尚处于不断发展完善之中,关于主客体互倚性的成对模式及其检验方法有望得到进一步的阐述与修正。
总之,APIM是一种非常有潜力的成对数据分析理论与方法。采用APIM不仅可用来分析横断数据,对于分析发展心理学研究中的追踪数据也十分有帮助 (Little & Card, 2005)。APIM的成对模式及其检验对成对关系研究,特别是家庭研究具有重要的意义。在家庭研究中,研究者关注的主要是夫妻 (父母)、亲子、兄弟姐妹之间的成对关系。Kenny等人在k值的介绍中,着重提出了对于家庭研究来说,具有特殊意义的三个取值 (0,1,-1)。对于APIM的成对模式及k值的分析检验可以在分析主体效应与客体效应的基础上,更为深入地探讨家庭过程,揭示家庭关系的实质。而GAPIM的成对模式在组织心理学的研究中则具有重要意义,有助于研究者揭示在组织情境中,个体特征的作用效果 (例如蛙池效应的检验)。主客体互倚性的成对模式分析对于成对数据研究,特别是家庭与组织心理学研究具有重要的应用价值。
| APIM kPaper. Retrieved March 8, 2015, from http://davidakenny.net/papers/k_apim/k_apim.htm |
| Cook W. L., & Kenny D. A. (2005). The Actor-Partner Interdependence Model:A model of bidirectional effects in developmental studies. International Journal of Behavioral Development, 29(2), 101-109. DOI: 10.1080/01650250444000405. |
| Garcia R. L., Meagher B. R., & Kenny D. A. (2015). Analyzing the effects of group members' characteristics:A guide to the group actor-partner interdependence model. Group Processes & Intergroup Relations, 18(3), 315-328. |
| Kenny D. A., & Cook W. (1999). Partner effects in relationship research:Conceptual issues, analytic difficulties, and illustrations. Personal Relationships, 6(4), 433-448. DOI: 10.1111/pere.1999.6.issue-4. |
| Kenny D. A., & Garcia R. L. (2012). Using the actor-partner interdependence model to study the effects of group composition. Small Group Research, 43(4), 468-496. DOI: 10.1177/1046496412441626. |
| Kenny D. A., Kashy D. A., & Cook W. L. (2006). Dyadic data analysis. New York: Guilford Press. |
| Kenny D. A., & Ledermann T. (2010). Detecting, measuring, and testing dyadic patterns in the actor-partner interdependence model. Journal of Family Psychology, 24(3), 359-366. DOI: 10.1037/a0019651. |
| Kivlighan Jr D. M., & Paquin J. D. (2014). Whose perceptions matter more:Mine or my group's? An actor-partner interdependence analysis disaggregating between-person and between-session effects of group climate perceptions on intimate behaviors. Journal of Counseling Psychology, 61(3), 333-339. DOI: 10.1037/cou0000025. |
| Little T. D., & Card N. A. (2005). On the use of social relations and actor-partner interdependence models in developmental research. International Journal of Behavioral Development, 29(2), 173-179. DOI: 10.1080/01650250444000388. |
| Ledermann T., Macho S., & Kenny D. A. (2011). Assessing mediation in dyadic data using the actor-partner interdependence model. Structural Equation Modeling:A Multidisciplinary Journal, 18(4), 595-612. DOI: 10.1080/10705511.2011.607099. |
| Mushquash A. R., Stewart S. H., Sherry S. B., Mackinnon S. P., Antony M. M., & Sherry D. L. (2013). Heavy episodic drinking among dating partners:A longitudinal actor-partner interdependence model. Psychology of Addictive Behaviors, 27(1), 178-183. DOI: 10.1037/a0026653. |
| Olsen J. A., & Kenny D. A. (2006). Structural equation modeling with interchangeable dyads. Psychological Methods, 11(2), 127-141. DOI: 10.1037/1082-989X.11.2.127. |
| Ponnet K., Mortelmans D., Wouters E., Van Leeuwen K., Bastaits K., & Pasteels I. (2013). Parenting stress and marital relationship as determinants of mothers' and fathers' parenting. Personal Relationships, 20(2), 259-276. DOI: 10.1111/j.1475-6811.2012.01404.x. |
| Rindskopf D. (1984). Using phantom and imaginary latent variables to parameterize constraints in linear structural models. Psychometrika, 49(1), 37-47. DOI: 10.1007/BF02294204. |
| Wickham R. E., & Knee C. R. (2012). Interdependence theory and the Actor-partner interdependence model:Where theory and method converge. Personality and Social Psychology Review, 16(4), 375-393. DOI: 10.1177/1088868312447897. |
| 陈玲玲, 伍新春, 刘畅. (2014). 父母的婚姻满意度对父亲教养投入的影响:父母协同教养的中介作用. 心理发展与教育, 30(3), 268-276. |
| 李育辉, 黄飞. (2010). 成对数据分析之行动者-对象互依性模型 (APIM). 心理科学进展, 18(8), 1321-1328. |
 2017, Vol. 33
2017, Vol. 33


