2. 西北大学 数学学院, 陕西 西安 710127
2. School of Mathematics, Northwest University, Xi′an 710127, China
对称性和守恒律一直都是数学和物理中的重要研究对象, 尤其是在孤立子理论和可积系统中, 对称性和守恒律更是发挥着重要的作用。对于一个方程如果含有无穷多守恒律, 则可认为此方程是可积的[1-2]。为了寻求守恒律, 德国女数学家Noether建立了变分对称群的理论, 并提出了著名的Noether定理[3], 说明了对称性与守恒律之前存在着对应关系。她指出,作用量的每一种对称性都对应着一个守恒定律, 如空间平移不变性对应动量守恒定律, 时间平移不变性对应着能量守恒定律。反之, 对于每一个守恒定律, 必对应有一种对称性。但是利用Noether定理求方程的守恒律, 必须要求方程为Euler-Lagrange型方程, 因此说明此方法具有一定的局限性。通过对此方法的进一步改进和推广, Ibragimov给出了伴随方程法[4-6], 该方法对于任意的线性或非线性微分方程, 可用来寻找与方程的Lie对称, Lie-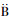
Lie对称分析是研究非线性偏微分方程最有效的方法之一。Lie的理论为分析研究偏微分方程提供了有效的工具, 并已得到了广泛的应用[18-21], 比如:利用Lie对称方法去求方程的精确解, 对方程进行分类, 约化方程的维数, 求方程的守恒律等等。
HBK方程组的具体形式如下
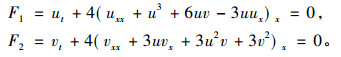
|
(1) |
方程组(1)最早是由楼森岳教授等推出并进行研究的[7], 它可以被看作是著名的Broer-Kaup方程组的推广, 通常被用来描述双向长波在浅水中的传播。文献[8]给出了方程组(1)的一些特殊解, 文献[9]研究了(1)的达布变换和多孤子解, 文献[10]研究了(1)的潘勒韦分析, 给出了新的解析解, 文献[11]利用相容的tanh函数展开(CTE)方法, 证明了方程组(1)是CTE可解的, 并给出了(1)在不同的非线性激发下一些相互作用解。本文主要研究方程组(1)的Lie对称分析、非线性自伴随及守恒律。
1 HBK方程的李群分析和最优系统 1.1 HBK方程的李群分析首先, 考虑方程组(1)的单参数Lie群的无穷小变换:
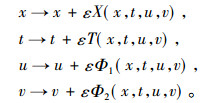
|
(2) |
其中, ε≪1为无穷小参数, 变换群式(2)对应的向量场为
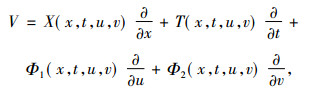
|
(3) |
如果向量场(3)是方程(1)的李对称, 即要求方程组(1)在变换
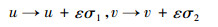
|
(4) |
下保持形式不变, σ1, σ2分别代表变量u, v所满足方程的对称, 表达式为
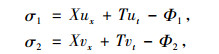
|
(5) |
它们需要满足的对称方程为
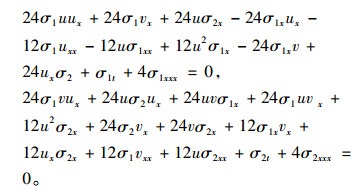
|
(6) |
把式(5)代入(6), 由初始条件消去ut, vt和它们的高阶导数项, 然后收集u, v的各阶导数项的系数, 令它们等于零, 得到一系列关于X, T, Φ1, Φ2的线性方程组, 借助于Maple软件可求得

|
(7) |
其中c1, c2, c3为任意常数。
基于表达式(7), 根据李群分析方法求得方程组(1)的所有向量场
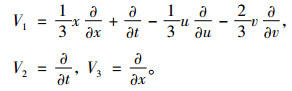
|
(8) |
在1.1中, 我们求出了方程组(1)的所有向量场如式(8)所示, 根据上面的向量场, 很容易验证它们关于李括号是封闭的。下面给出李代数交换子表(见表 1)。
|
|
表 1 李代数交换子表 Tab. 1 The commentator table of Lie algebra |
其中
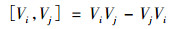
|
(9) |
表示的是李代数交换子。最优系统的李级数公式
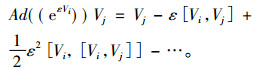
|
(10) |
其中ε是实常数, [Vi, Vj]如式(9)所示,由表 1和公式(10)可求得李代数伴随表(见表 2)。
|
|
表 2 李代数伴随表 Tab. 2 The ajoint table of Lie algebra |
根据表 2, 我们可以求出方程组(1)的一维子代数最优系统分别是
1) V3;
2) aV1+bV2, 当a∈{-1, 0, 1}时, b∈R, 当a=0时, b∈{-1, 0, 1}。
2 HBK方程的自伴随性定义1[6] 方程组
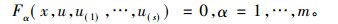
|
(11) |
其中x=(x1, x2, …,xn), u=(u1, u2, …,um),u(s)表示的是u关于自变量的s阶偏导数。方程组(11)的伴随方程是
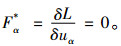
|
(12) |
其中
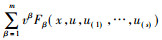
定义2[6] 方程组(11)被称为是自伴随的如果其伴随方程组(12)在变换vβ=um下等于方程组(11)。
定义3[6] 方程组(11)被称为是非线性自伴随的, 如果其伴随方程组(12)满足下面的方程组
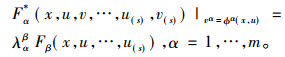
|
(13) |
其中ϕ(x, u)≠0, λαβ是待定系数, ϕ=(ϕ1, …,ϕm)表示的是m维的向量。
根据定义1可求得方程组(1)的伴随方程为
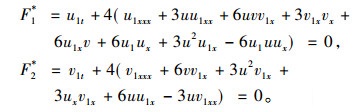
|
(14) |
其标准的Lagrangian为
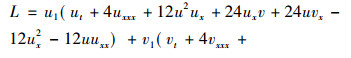
|

|
(15) |
其中u1=u1(x, t), v1=v1(x, t)为新的因变量。
根据定义2可知, 方程组(1)不是自伴随的。根据定义3, 如果能找到u1=ϕ(x, t, u, v), v1=φ(x, t, u, v)满足方程组(13), 其中ϕ(x, t, u, v), φ(x, t, u, v)不全为零, 则说明方程组(1)是非线性自伴随的。换言之,方程组(1)是非线性自伴随的, 如果伴随方程满足下面的条件

|
(16) |
将方程组(1), (14)代入方程组(16)中, 因为ϕ, φ不依赖于导数ut, vt, uxx, vxx,…, 方程组(16)关于系数λij(i, j=1, 2)可以分解为如下的方程组
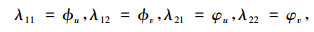
|
(17) |
将式(17)再代入式(16)可得如下的超定方程组

|
通过解以上的方程组可得
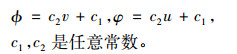
|
(18) |
c1, c2是任意常数。
因此, 方程组(1)在代换(18)下是非线性自伴随的。
3 HBK方程的守恒律定理1[5] 方程组(1)的任何一个Lie点对称, Lie-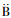
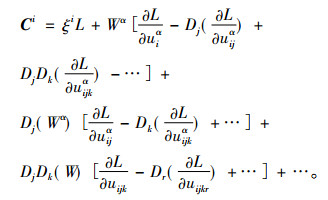
|
(19) |
其中Wα=ηα-ξjujα。
根据定理1给出的结论, 设向量场的通式为
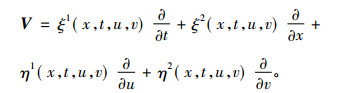
|
根据算子V可以推导出守恒律Dt(C1)+Dx(C2)=0, 其中守恒向量C=(C1, C2)的分量C1, C2是由式(19)给出的, 具体的表达式如下:
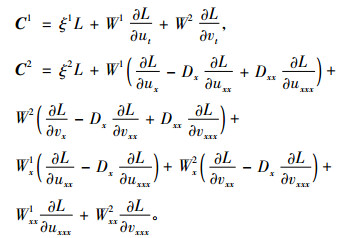
|
化简后为
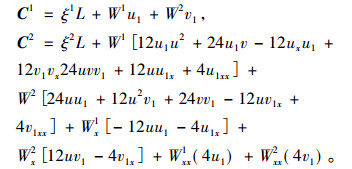
|
(20) |
下面分情况讨论。
情形1 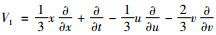
此时, 可以求得
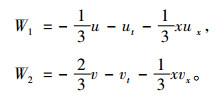
|
(21) |
将式(15), (21)代入式(20)可以求得方程组(1)的守恒向量场为
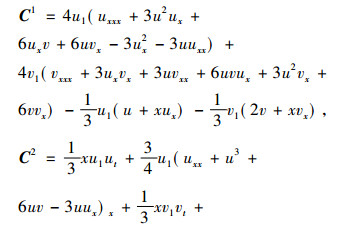
|

|
情形2 
此情形下, 可求得
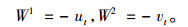
|
(22) |
将式(15), (22)代入式(20)可以求得方程组(1)的守恒向量场为
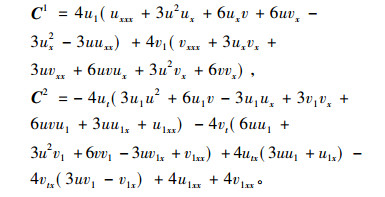
|
情形3 
此情形下, 可求得
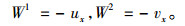
|
(23) |
将式(15), (23)代入式(20)可以求得方程组(1)的守恒向量场为
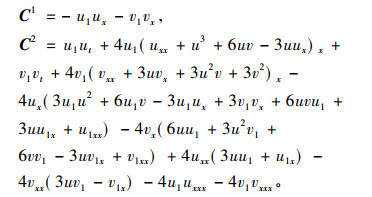
|
通过上面的讨论, 我们发现, 每一种情形下求出的守恒向量都含有伴随方程中的任意函数u1, v1, 因此他们给出了方程组(1)的无穷多守恒律。
4 结论本文利用李群分析方法求出了HBK方程组(1)的Lie对称及最优系统。其次利用Ibragimov的相关理论证明了(1)是非线性自伴随的, 然后利用(1)的伴随方程, Lie对称求出了方程组(1)的无穷多守恒律。求出的守恒律对于研究方程的可积性具有重要的意义。
| [1] |
BLUMAN G W, KUMEI S. Symmetries and differential equations[M]. New York: Springer-Verlag, 1989.
|
| [2] |
ADEM A R, KHALIQUE C M. Symmetry reductions, exact solutions and conservation laws of a new coupled KdV system[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(9): 3465-3475. DOI:10.1016/j.cnsns.2012.01.010 |
| [3] |
NOETHER E. Invariante variations problem[J]. Transport Theory and Statistical Physics, 1971, 1(3): 186-267. DOI:10.1080/00411457108231446 |
| [4] |
IBRAGIMOV N H. Integrating factors, adjoint equations and Lagrangians[J]. Journal of Mathematical Analysis Applications, 2006, 318(2): 742-757. DOI:10.1016/j.jmaa.2005.11.012 |
| [5] |
IBRAGIMOV N H. A new conservation theorem[J]. Journal of Mathematical Analysis Applications, 2007, 333(1): 311-328. DOI:10.1016/j.jmaa.2006.10.078 |
| [6] |
IBRAGIMOV N H. Nonlinear self-adjointnss and conservation laws[J]. Journal of Physics A: Mathematical and Theoretical, 2001, 44(43): 1-8. |
| [7] |
LOU S Y, HU X B. In_ nitely many lax pairs and symmetry constraints of the KP equation[J]. Journal of Mathematical. Physics, 1997, 38(12): 6401-6427. DOI:10.1063/1.532219 |
| [8] |
FAN E G. Solving Kadomtsev-Petviashvili equation via a new decomposition and Darboux transformation[J]. Communications in Theoretical Physics, 2002, 37(2): 145-148. DOI:10.1088/0253-6102/37/2/145 |
| [9] |
HUANG D J, lI D S, ZHANG H Q. Explicit n-fold Darboux transformation and multisoliton solutions for the (1+1)-dimensional higher-order Broer-Kaup system[J]. Chaos, Solitons & Fractals, 2007, 33(5): 1677-1685. |
| [10] |
LI X N, WEI G M, LIU Y P. Painleve analysis and new analytic solutions for (1+1)-dimensional higher-order Broer Kaup system with symbolic computation[J]. International Journal of Modern Physics B, 2014, 28(14): 1450067. DOI:10.1142/S0217979214500672 |
| [11] |
XIN X P. Interaction solution for (1+1)-dimensional higer-order Broer-Kaup system. arXiv: 1512.08329v1.
|
| [12] |
CAO Z J, LIN Y P. Lie point symmetries, conservation laws, and solutions of a space dependent reaction-diffusion equation[J]. Applied Mathematics and Computation, 2014, 248: 386-398. DOI:10.1016/j.amc.2014.09.093 |
| [13] |
WANG G W. Lie symmetry analysis, nonlinear self-adjointness and conservation laws to an extended (2+1)-dimensional Zakharov-Kuznetsov-Burgers equation[J]. Computers & Fluids, 2015, 119(22): 143-148. |
| [14] |
MUHAMMAD A A. Nonlinear self-adjointness and conservation laws of the (3+1)-dimensional Burgers equation[J]. Wave Motion, 2015, 57: 34-43. DOI:10.1016/j.wavemoti.2015.03.003 |
| [15] |
TRACINÀ R, BRUZÓN M S, GANDARIAS M L, et al. Nonlinear self-adjointness, conservation laws, exact solutions of a system of dispersive evolution equations[J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(9): 3036-3043. DOI:10.1016/j.cnsns.2013.12.005 |
| [16] |
XIA Y R, XIN X P, ZHANG S L. Nonlinear self-adjointness, conservation laws and Soliton-Cnoidal wave interaction solutions of the (2+1) dimensional modified dispersive Water-Wave systems[J]. Communications in Theoretical Physics, 2017, 67(1): 15-21. DOI:10.1088/0253-6102/67/1/15 |
| [17] |
XIA Y R, XIN X P, ZHANG S L. Residual symmetry, interaction solutions, and conservation laws of the (2+1)-dimensional dispersive long-wave system[J]. Chinese Physics B, 2017, 26(3): 030202. DOI:10.1088/1674-1056/26/3/030202 |
| [18] |
夏亚荣. 广义非线性扩散方程的条件Lie-backlund对称和不变子空间[J]. 西北大学学报(自然科学版), 2016, 46(1): 19-23. |
| [19] |
夏亚荣. 反应扩散方程组的条件Lie-backlund对称和不变子空间[J]. 陕西师范大学学报(自然科学版), 2016, 44(5): 13-20. |
| [20] |
黄晴. Novikov方程的对称群分析[J]. 西北大学学报(自然科学版), 2015, 45(1): 10-13. |
| [21] |
黄晴. 一类四阶非线性方程的Galilei对称分类问题[J]. 西北大学学报(自然科学版), 2013, 43(5): 697-699. |
 2017, Vol. 47
2017, Vol. 47