随着地震波逆时成像技术的研发和规模化应用, 其在复杂波场和复杂构造的精确成像中已取得了显著的地质效果, 得到了研究人员的广泛重视。逆时成像技术是一种利用双程地震波波动方程并结合高阶逼近的数值离散算法, 有效解决了多路径传播、多次波归位、大倾角陡倾角成像、回转波成像、棱柱波成像以及保幅地震成像等关键技术问题, 适合于速度和构造变化较为剧烈的复杂波场高精度成像, 有效解决了克希霍夫积分法深度偏移和单程波动方程深度偏移等方法无法实现的复杂波场准确归位的难题, 因此, 具有明显的地震成像技术优势。随着近几年CPU/GPU等高性能计算技术、超算平台的规模应用和海量并行存储技术的快速发展, 逆时成像技术已突破了海量存储和庞大计算量等一系列技术瓶颈, 实现了规模化生产应用, 并有效支撑了复杂地质目标的勘探和开发工作[1]。
与其它深度域地震成像方法不同, 逆时成像方法的显著特点是成像中存在较强能量的低波数背景噪声, 该噪声严重掩盖了有效反射信号, 因而制约了复杂地质目标的精细刻画。同时这类噪声通常被报道为“低频”噪声, 这是用时间域的频谱分析手段分析深度域的数据引入的概念, 而逆时偏移结果实际为深度域数据体, 因此用低波数噪声来描述此类噪声更为合理。国内外学者针对这类噪声的成因已形成一些认识, 例如该噪声是由炮点和检波点同方向传播波场沿着传播路径相关成像而引入等。目前压制这类噪声的方法主要有2种思路[2]。①在成像过程中进行优化, 即在炮点和检波点波场延拓成像过程中施加一定的约束。例如FLETCHER等[3]在地震波动方程中引入衰减项压制背向散射波; XIE等[4]利用单程波算子分离不同方向的地震波场; YOON等[5]通过采用波印廷矢量计算波场传播方向, 并选择传播方向相反的炮点和检波点波场进行成像; BAYSAL等[6]采用无反射波动方程, 但其只能去除垂直入射方向形成的噪声; LOEWENTHAL等[7]采用大于波长长度的窗函数对速度模型慢度进行平滑; GUITTON等[8]采用最小二乘方法压制了逆时偏移噪声; LIU等[9]采用行波分离成像条件压制了低波数噪声。②在成像后进行去噪。例如高通滤波方法[10], 其计算效率高, 但缺点是存在吉布斯效应且适合于时间域数据处理, 而在深度域直接应用时则没有完备的理论依据, 同时由于其是逐道滤波, 去噪后结果存在逐道处理痕迹, 因此横向不保幅; 导数滤波方法可以去除近零波数成分的干扰能量, 但相位会发生改变, 且高频噪声被显著增强, 信噪比降低; Laplacian去噪方法[11]可以压制入射角接近90°时的背景噪声, 但其对其它角度形成的干扰压制效果较差, 且同样存在不保幅和对噪声敏感、相位发生改变等问题。
偏微分方程(PDE)方法是20世纪90年代初兴起的一种新的信号处理技术, 在热力学领域和图像处理领域得到了广泛应用, 其中扩散滤波方法最具代表性。该方法的应用机理源于物理中的热扩散现象, 正如我们能将热源在不同时刻的分布特征清楚地描绘出来一样, 将输入的待处理图像作为初始条件, 通过解关于时间的偏微分方程(扩散方程)得到预定扩散时间后的图像, 只是需要根据图像的局部特点, 在扩散过程中施加约束条件, 从而实现可控扩散滤波处理。目前扩散滤波方法已在地震勘探领域中逐渐发挥了重要作用, 例如利用基于断层算子的各向异性扩散滤波提高地震数据品质[12]、缺失地震数据的修复和重建[13]、基于不连续性的三维各向异性扩散滤波方法识别断层[14]、地震反射波和散射波的相对分离[15-16]等。
为此, 在前人研究的基础上, 首次将三维扩散滤波方法引入到深度域逆时偏移低波数噪声压制中, 首先对含低波数噪声地震逆时成像数据体进行体迭代处理, 通过试验优化迭代次数和扩散系数2个关键参数, 实现低波数噪声和有效反射信号的相对保幅分离, 同时采用局部化数据体输入和临时输出存储优化策略研发了功能模块, 突破了计算节点内存限制, 构建了一种高效的、相对保幅的深度域低波数噪声压制技术。最后用理论模型和实际资料进行应用测试, 为同类深度域含低波数噪声资料地质目标的地震精细刻画提供方法指导。
1 基本原理 1.1 低波数噪声成因分析与克希霍夫偏移等其它深度域地震成像方法不同, 基于地震双程波动方程的逆时偏移方法具有较强能量的低波数背景噪声, 该噪声掩盖了有效的地层反射信号。国内外诸多学者研究表明[17], 形成该低波数噪声的原因主要是由不同传播方向的震源波场和检波点波场在波场延拓过程中的每一条传播路径上的每一个空间位置互相关计算产生, 而相同传播方向的震源波场和检波点波场的互相关计算能够有效提高成像结果的精度和信噪比, 后者可以实现在逆时偏移延拓过程中压制一部分低波数背景噪声, 但不能完全消除。
1.2 低波数噪声衰减方法将热力学领域的扩散滤波方程引入到地震勘探领域逆时偏移低波数噪声压制中, 实现了低波数噪声和有效反射信号的相对保幅分离处理[10], 其微分形式的计算公式如下:
| $ \begin{gathered} \frac{\partial U}{\partial t}=\alpha \cdot \nabla^2 U, \left.U\right|_{t=0}=U_0 \\ U_{\mathrm{e}}=U_0-U \end{gathered} $ | (1) |
式中: t为扩散时间, 忽略时间步长可用迭代次数N代替; α为扩散系数;
对于含低波数噪声的逆时偏移数据体, 可用扩散滤波方程将局部地震数据的能量进行重新分配, 通过多次数据体迭代处理, 直到地震能量达到均衡为止, 其中扩散系数和扩散时间取值越大, 则地震能量扩散的程度越强, 经扩散滤波处理后的地震数据越平滑, 越接近于平稳状态, 即为低波数背景噪声, 反之亦然[12]。因此, 扩散滤波方法是一种全局的、非线性体迭代滤波处理方法, 主要受迭代次数和扩散系数2个关键参数控制, 可以采用确定其中一个关键参数(通常固定扩散系数α), 同时调节另一个关键参数(通常迭代次数N)进行参数试验, 由此获得不同分离尺度的低波数噪声和有效反射信号的相对分离结果。
2 算法优化与模块研发对(1)式采用二阶时间和空间中心式有限差分法进行数值离散化[18], 具体公式如下:
| $ \begin{gathered} U_{i, j, k}^{t+1}=U_{i, j, k}^t+\alpha\left(U_{i+1, j, k}^t+U_{i-1, j, k}^t+U_{i, j+1, k}^t+\right. \\ \left.U_{i, j-1, k}^t+U_{i, j, k+1}^t+U_{i, j, k-1}^t-6 U_{i, j, k}^t\right) \end{gathered} $ | (2) |
式中: i, j, k分别为x, y, z这3个空间方向的网格点位置。
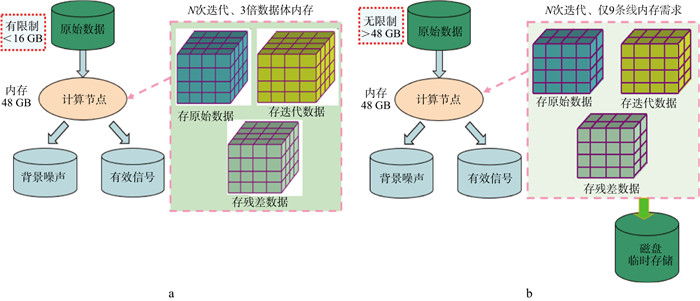
2.1 算法优化策略若采用(2)式进行技术模块研发, 需要在计算节点的内存中开辟至少3个U数据体(含低波数噪声数据体)的存储空间, 用于存储t和t+1时刻的U数据体及两者的残差数据体, 当计算节点内存小于3倍U数据体的存储空间时, 无法完成处理(图 1a)。为此, 采用部分线数据输入和临时输出存储的策略[19]进行优化: 先将相邻3条线数据从数据盘读入内存(L1、L2、L3), 采用(2)式计算中间线数据, 得到M2并输出至临时盘存储, 接着将L4从数据盘读入内存, 通过数据替换, 重新形成(L2、L3、L4), 采用(2)式计算中间线数据, 得到M3并输出至临时盘存储, ……, 依此类推, 完成第一轮所有线数据的迭代计算; 接着将相邻3条线数据从临时盘读入内存(M1、M2、M3), 采用(2)式计算中间线数据, 得到K2并输出至临时盘存储, 接着将M4从数据盘读入内存, 通过数据替换, 重新形成(M2、M3、M4), 采用(2)式计算中间线数据, 得到K3并输出至临时盘存储, ……, 依此类推, 完成第N轮所有线数据的迭代计算, 得到最终的处理结果。采用局部化的数据输入和临时输出存储的优化策略可以在保持处理周期情况下, 突破计算节点内存的技术瓶颈, 形成该技术的工业化规模应用能力(图 1b)。
|
图 1 优化前(a)和优化后(b)扩散滤波处理技术模块实施过程 |
根据2.1节的优化策略, 成功研发了适应性能更高、基于CPU加速的技术功能软件模块(可执行代码): ckyseparation, 并在Linux工作站平台上完成了大量数据的准确性测试和实际地震资料应用, 该技术模块的一个脚本作业如表 1所示(以Linux平台命令行运行方式)。
| 表 1 ckyseparation技术模块的一个脚本作业 |
表 1中ckyseparation为研发的模块名; sgyin代表输入SEGY格式的数据体文件名; sgyoutref代表输出的SEGY格式低波数噪声文件名; sgyoutsca代表输出的SEGY格式有效反射信号文件名; diffupara和internum为本文技术的2个关键参数, 分别代表扩散系数和迭代次数; tmpdir=/tmp/ 代表作业临时输出文件夹名, 该选项突破了该技术受计算节点内存大小的限制, 适应海量数据体处理; rmflag代表在作业结束后临时存储文件是保留(1)还是删除(0)。
大量理论模型数据和实际地震资料应用结果表明, 这项技术在关键参数选择上, 可以采用固定扩散系数, 调节迭代次数的方式来实施, 通常情况下采用迭代次数为100、扩散系数为1.0可以获得较好的低波数噪声相对保幅衰减效果。
在三维地震数据体应用效率方面, 处理周期与待处理数据体的大小呈正相关, 50 GB地震数据体完成100次迭代处理, 且不受计算机节点的内存大小限制(可以小于2 GB), 处理周期可控制在1天以内, 完全可以满足实际资料的应用需求。
目前, 该技术模块已在大庆探区松辽深层、海拉尔及外围、塔东等领域20个以上地震工区进行了测试和推广应用, 验证了ckyseparation处理模块的稳定性、衰减低波数噪声的保真保幅性, 以及实现复杂地质目标地震精细刻画的能力。
3 理论模型数据测试以二维Marmousi模型为例(图 2a), 模型的长和宽分别为3.4 km和1.4 km, 模型网格横向和纵向均为5 m, 最小介质速度为1 028 m/s, 最大介质速度为4 670 m/s, 采用主频为30 Hz的雷克子波作为激发震源, 在模型地表距离最左侧900 m处开始往右侧移动激发, 炮间距为10 m, 共激发251炮, 每道接收时长为3s, 正演数值模拟的时间步长为0.2 ms, 所有检波点布置于整个模型地表, 道间距为5 m, 即每炮共180道接收。采用16阶精度的交错网格有限差分法提高波动方程正演数值模拟精度和逆时延拓精度, 采用10个网格点的PML吸收边界条件有效压制人为截断边界引入的干扰波。上述正演采集观测系统共采集得到251个炮集记录, 通过逆时偏移处理(采用互相关逆时成像条件和精确的速度模型), 获得含低波数噪声的逆时偏移结果(图 2b)。

|
图 2 Marmousi理论模型及两种方法压制低波数噪声应用效果对比 a Marmousi模型; b 含低波数噪声的逆时偏移结果; c 图 1b经扩散滤波处理后的有效信号; d 图 1b经扩散滤波处理掉的噪声分量; e 图 1b经拉普拉斯算子去噪处理后的有效信号; f 图 1b经拉普拉斯算子去噪处理掉的噪声分量 |
分析图 2b可知, 逆时偏移实现了Marmousi模型中复杂构造内断层、断点、不整合等地质界面的准确成像, 其成像结果与偏移速度模型特征基本一致, 但由于低波数噪声的存在, 使得地层接触关系变得模糊不清, 对地层细节的刻画不够精细, 因此降低了成像精度。
对图 2b所示结果应用本文方法处理后(处理参数: 迭代次数为100, 扩散系数为1.0), 有效信号和低波数噪声得到了相对保幅分离, 分离出的有效信号信噪比较高(图 2c), 地层接触关系和地层细节变得清晰明确, 且其波组特征与分离前的逆时成像剖面波组特征基本一致; 分离出的低波数噪声几乎不含有效信号(图 2d), 同时清晰展现了波动方程射线传播路径。分析还可知, 低波数噪声的能量在浅层位置比在深层强, 且其能量强弱与地层的反射系数大小呈正相关关系, 其中, 反射系数越高, 对应该界面上覆地层的低波数背景噪声也越强, 反之亦然。
采用国际上普遍应用的拉普拉斯算子去噪方法压制低波数噪声后, 分离出的有效信号视分辨率明显提高(图 2e), 但与原始逆时成像剖面相比, 其波组特征差异较大, 主要表现为地震同相轴的边缘被锐化, 主要原因在于拉普拉斯算子去噪方法是一种图像处理方法, 对振幅变化位置较为敏感, 振幅突变位置锐化现象更为严重; 与此同时, 分离出的低波数噪声波组特征与分离前的逆时成像剖面特征相一致(图 2f), 由此表明, 拉普拉斯算子去噪方法的保幅性能较差。
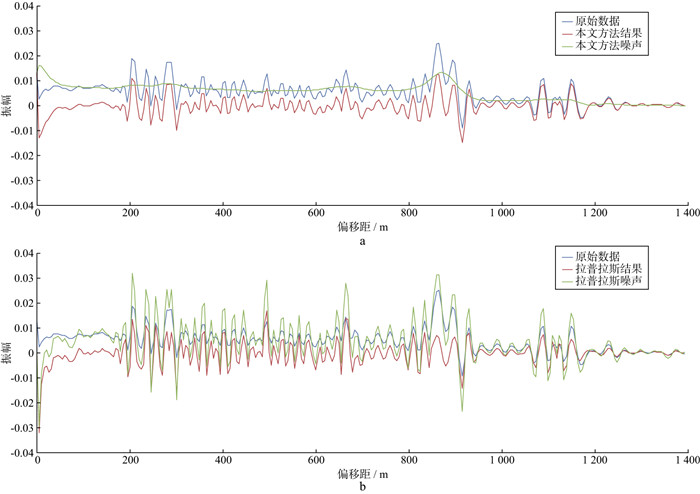
图 3a为图 2b经扩散滤波方法去噪前和去噪后及残差波形曲线(横坐标1 km位置处), 图 3b为图 2b经拉普拉斯算子去噪方法去噪前和去噪后及残差波形曲线(横坐标1 km位置处)。分析可知, 分离前的逆时偏移波形曲线浅层基本偏离了幅值为0的基线, 主要原因是该结果叠加了低波数噪声, 而采用扩散滤波方法处理后, 低波数噪声被相对保幅地分离和压制, 使分离出的有效信号恢复到了幅值为0的基线, 同时保留了波场能量的相对变化关系; 而采用拉普拉斯算子去噪方法分离后, 分离出的有效信号波形曲线存在抖动特征(经相位反转处理, 使得波形与分离前一致), 波场曲线呈现尖锐化现象, 分离出的噪声与分离前逆时成像波形曲线特征基本一致, 也增加了锐化特征。综上分析可知, 与拉普拉斯算子去噪方法相比, 本文方法处理后的结果具有更高的保真、保幅性。
|
图 3 图 2b中横坐标1 km位置处不同去噪方法对应成像波形曲线 a 扩散滤波方法去噪前和去噪后及残差波形曲线; b 拉普拉斯算子去噪方法去噪前和去噪后及残差波形曲线 |
以大庆探区B工区为例, 该地区属于断陷盆地, 构造非常发育, 且地震资料信噪比较低。地质任务是落实目的层构造形态、幅度、类型及位置, 准确落实断层及其空间分布状况, 研究目的层的断裂特征, 落实基底起伏状态, 研究构造发育史及演化规律, 以及断裂、构造与油气的运聚关系。为了提高B工区地震成像质量, 在高精度速度建模和叠前保幅预处理基础上, 开展了高精度逆时偏移处理[20], 在逆时成像过程中已采用行波分离的逆时成像条件压制了成像过程中的低波数噪声, 但最终的成像结果仍存在一定能量的残余低波数噪声, 该噪声掩盖了复杂地质目标的细节。
图 4a为含低波数噪声的逆时偏移剖面及波数谱。分析可知, 整个成像剖面信噪比较低, 且断陷盆地及其内部地层结构被强能量的低波数噪声掩盖, 地层接触关系刻画不清晰, 在波数谱的低波数端清晰可见较强的能量团。图 4b为采用拉普拉斯算子去噪方法压制低波数噪声后的逆时偏移剖面及其波数谱, 其中波数谱是由深度域逆时成像剖面采用某商业地震处理软件中时间域二维频谱分析得到, 因此纵坐标显示为频率, 横坐标显示为波数。分析可知, 除了向右侧倾斜的大断面得到清晰刻画外, 其它剖面位置的同相轴不连续, 信噪比低, 几乎看不到断陷盆地内部地层接触关系, 同时其波数谱的低波数端能量已被完全压制, 并显著增强了高波数端能量。由此可见, 该方法保幅性差, 且对信噪比低的地震资料效果不明显。图 4c为采用本文扩散滤波方法压制低波数噪声后的逆时偏移剖面及波数谱(处理参数: 迭代次数为100, 扩散系数为1.0)。分析可知, 断陷盆地及其内部地层结构得到精细刻画, 地层接触关系刻画清晰, 在波数谱的低波数端能量团得到了有效压制, 且高波数端能量得到了有效保持。由此表明, 本文扩散滤波方法对输入资料的噪声不敏感, 因此, 具有更好的保幅性和适应性, 可以获得更加精细、保真的处理结果。

|
图 4 B工区两种方法压制低波数噪声应用效果对比 a 含低波数噪声的逆时偏移剖面及波数谱; b 拉普拉斯算子去噪方法压制低波数噪声后的逆时偏移剖面及波数谱; c 扩散滤波方法压制低波数噪声后的逆时偏移剖面及波数谱 |
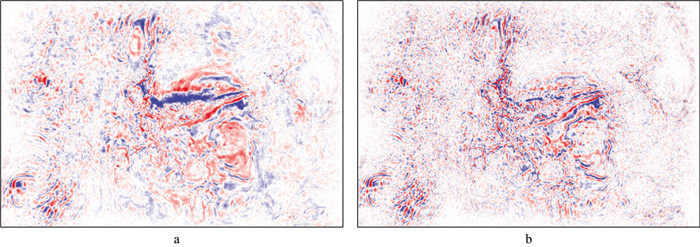
BX工区属于地震资料信噪比较高的复杂断陷盆地, 通过复杂小断块的精确成像, 厘清断层、断点的接触关系, 落实研究区复杂断裂特征, 支撑井位目标优选。图 5和图 6分别给出了在BX工区采用扩散滤波方法压制低波数噪声前、后的逆时偏移剖面和等深度切片。其中, 图 5a和图 6a分别为含低波数噪声的逆时偏移剖面和等深度切片。分析可知, 逆时偏移剖面已实现了复杂构造及断点、断面的准确成像, 但较强能量的低波数噪声掩盖了有效反射信号, 主要表现为同相轴波形较粗, 地层细节刻画不清晰, 地层接触关系不明确, 制约了对该地区复杂构造特征及其展布的整体认识。为此, 采用扩散滤波方法进行处理(处理参数: 迭代次数为80, 扩散系数为1.0), 图 5b和图 6b分别为低波数噪声衰减后的逆时偏移剖面和等深度切片。低波数噪声得到了明显压制, 地层接触关系更加清晰明确, 地层细节刻画更加精细, 恢复了复杂盆地边界及内部结构特征, 提高了复杂地质目标的横纵向精细刻画能力。由此验证了本文扩散滤波方法在深度域可以达到高信噪比、高精细度、保幅保真的应用效果, 实现了对复杂地质目标的精细刻画。

|
图 5 BX工区采用扩散滤波方法压制低波数噪声前(a)、后(b)逆时偏移剖面 |
|
图 6 BX工区采用扩散滤波方法压制低波数噪声前(a)、后(b)等深度切片 |
1) 根据逆时偏移噪声具有低波数特征, 研发了一种基于扩散滤波的深度域相对保幅的低波数噪声压制方法, 并采用局部化数据输入和临时输出存储的优化策略, 研发形成了高性能计算处理模块, 突破了大数据体迭代处理受计算节点内存影响的瓶颈, 满足了实际应用需求;
2) 实现了深度域地震数据体的低波数噪声和有效反射信号的相对保幅分离处理, 该方法主要受扩散滤波和迭代次数2个关键参数控制, 通常通过固定扩散滤波参数, 试验选择合适的迭代次数, 在深度域实现强能量低波数噪声的有效衰减, 并相对保幅地恢复出掩盖在低波数噪声之下的有效反射信号;
3) 低波数噪声剖面展示出波动方程的射线传播路径, 其能量在浅层位置比在深层强, 能量强弱与地层的反射系数大小呈正相关关系, 反射系数越高, 对应该界面上覆地层的低波数背景噪声越强, 反之亦然;
4) 理论模型和实际资料应用结果均表明, 基于扩散滤波方法可以相对保幅地分离出低波数噪声, 与传统的拉普拉斯算子去噪方法相比, 其处理后的结果具有更高的保真保幅性, 深度域地震数据体的分辨率和信噪比更高, 复杂地质目标的横向和纵向刻画更加精细, 可以满足深度域地震数据体不同信噪比低波数噪声的相对保幅处理和精细刻画地质目标的应用需求。
| [1] |
陈可洋. 高阶弹性波波动方程正演模拟及逆时偏移成像研究[D]. 大庆: 大庆石油学院, 2009 CHEN K Y. High-order elastic wave equation forward modeling and reverse-time migration[D]. Daqing: Daqing Petroleum Institute, 2009 |
| [2] |
陈可洋. 基于行波分离和角度域衰减的地震波叠前逆时成像条件[J]. 计算物理, 2016, 33(2): 205-211. CHEN K Y. Seismic wave pre-stack reverse-time migration imaging condition based on one-way wave field separation and angle domain attenuation[J]. Chinese Journal of Computational Physics, 2016, 33(2): 205-211. |
| [3] |
FLETCHER R P, FOWLER P J, KITCHENSIDE P. Suppressing artifacts in prestack reverse time migration[J]. Expanded Abstracts of 75th Annual Internat SEG Mtg, 2005, 2049-2051. |
| [4] |
XIE X, WU R. A depth migration method based on the full-wave reverse-time calculation and local one-way propagation[J]. Expanded Abstracts of 76th Annual Internat SEG Mtg, 2006, 2333-2337. |
| [5] |
YOON K, MARFURT K J. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 2006, 37(1): 102-107. DOI:10.1071/EG06102 |
| [6] |
BAYSAL E, KOSLOFF D, SHERWOOD J. Reverse-time migration[J]. Geophysics, 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [7] |
LOEWENTHAL D, MUFTI R. Reverse time migration in spatial frequency domain[J]. Geophysics, 1983, 48(5): 627-635. DOI:10.1190/1.1441493 |
| [8] |
GUITTON A, KAELIN B, BIONDI B. Least-squares attenuation of reverse-time migration artifacts[J]. Geophysics, 2007, 72(1): S19-S23. DOI:10.1190/1.2399367 |
| [9] |
LIU F Q, ZHANG G, MORTON S A, et al. Reverse-time migration using one way wavefield imaging condition[J]. Expanded Abstracts of 77th Annual Internat SEG Mtg, 2007, 2170-2174. |
| [10] |
陈可洋. 一种相对保幅的低频逆时噪声压制方法及其应用[J]. 油气藏评价与开发, 2014, 4(3): 50-54. CHEN K Y. A relative amplitude preservation low-frequency reverse-time noise suppression scheme and its application[J]. Reservoir Evaluation and Development, 2014, 4(3): 50-54. |
| [11] |
ZHANG Y, JAMES S. Practical issues of reverse time migration: true amplitude gathers, noise removal and harmonic source encoding[C]. CPS/SEG Beijing 2009 International Geophysical Cofference & Exposition, 2009: 5
|
| [12] |
李福强, 周东红, 明君, 等. 利用基于断层算子的各向异性扩散滤波提高地震数据品质[J]. 石油地球物理勘探, 2018, 53(6): 1137-1141. LI F Q, ZHOU D H, MING J, et al. Seismic data quality improvement with the anisotropic diffusion filter based on fault operator[J]. Oil Geophysical Prospecting, 2018, 53(6): 1137-1141. |
| [13] |
陈可洋, 陈树民, 李来林, 等. 基于扩散滤波的地震数据修复技术[J]. 计算物理, 2014, 31(4): 465-470. CHEN K Y, CHEN S M, LI L L, et al. Seismic data repair technology based on diffusion filtering method[J]. Chinese Journal of Computational Physics, 2014, 31(4): 465-470. |
| [14] |
王静, 张军华, 冯德永, 等. 利用不连续性的各向异性扩散滤波方法识别断层[J]. 石油地球物理勘探, 2020, 55(6): 1349-1357. WANG J, ZHANG J H, FENG D Y, et al. Fault identification based on a discontinuous anisotropic diffusion filter[J]. Oil Geophysical Prospecting, 2020, 55(6): 1349-1357. |
| [15] |
陈可洋, 杨微, 吴清岭, 等. 地震反射波与散射波波场分离方法初探[J]. 岩性油气藏, 2013, 25(2): 76-81. CHEN K Y, YANG W, WU Q L, et al. Preliminary study on seismic reflection wave and scattered wave wavefield separating scheme[J]. Lithologic Reservoirs, 2013, 25(2): 76-81. |
| [16] |
陈可洋. 地震波数据分离方法、装置及存储介质: 中国, 201811184216.2[P]. 2020-06-09 CHEN K Y. Seismic wave data separation method, device and storage medium: China, 201811184216.2[P]. 2020-06-09 |
| [17] |
宋宗平, 陈可洋, 杨微, 等. 地震波逆时偏移中两种成像条件应用效果对比[J]. 物探与化探, 2019, 43(3): 618-625. SONG Z P, CHEN K Y, YANG W, et al. Comparison of the application effect of two imaging conditions in seismic wave reverse time migration[J]. Geophysical and Geochemical Exploration, 2019, 43(3): 618-625. |
| [18] |
陈可洋. 三维扩散滤波方法地震数据处理模块的开发与应用[J]. 油气地球物理, 2014, 12(2): 26-30. CHEN K Y. Seismic data processing module development and application with 3D diffusion filtering scheme[J]. Petroleum Geophysics, 2014, 12(2): 26-30. |
| [19] |
陈可洋. 地震波数据的低波数噪音分离方法、装置及存储介质: 中国, 201811184185.0[P]. 2020-06-09 CHEN K Y. Low wavenumber noise separation method, device and storage medium of seismic wave data: China, 201811184185.0[P]. 2020-06-09 |
| [20] |
陈可洋. 逆时成像技术在大庆探区复杂构造成像中的应用[J]. 岩性油气藏, 2017, 29(6): 91-100. CHEN K Y. Application of reverse-time migration technology to complex structural imaging in Daqing exploration area[J]. Lithologic Reservoirs, 2017, 29(6): 91-100. |



