风洞天平是风洞测力试验中最重要的测量装置，用于测量飞行器模型上气动载荷的大小和作用点。一杆天平自设计、加工和贴片后，在投入风洞试验之前，必须进行地面静态校准，得到天平载荷输入和信号输出的对应关系，即天平公式。静态校准的质量直接决定了风洞试验数据结果的质量。为有效表征和衡量静态校准的质量，在天平完成校准后，需给出天平校准的不确定度。除此之外，天平校准不确定度是风洞试验不确定度的主要来源[1]，合理评估天平校准不确定度，也是系统分析风洞试验气动力数据不确定度的前提。
各行业的不确定度评估工作，历来难点不在于缺乏好的评估方法，难点在于研究人员和工程设计人员如何在应用这些方法的过程中保持一致性和规律性[2]，即不确定度评估的标准化。对于天平校准不确定度的评估，传统方法一直是将校准的实验标准偏差作为不确定度的近似结果[3, 4, 5, 6]。近年来，国内外各气动机构在天平校准不确定度的评估上逐渐开展了一些研究工作。国内的《风洞应变天平规范》阐述了校准不确定度有5个来源[7]。国外的天平校准不确定度评估主要是基于风洞试验的不确定度评估思想[8, 9, 10]。国内外已有的研究工作对天平校准不确定度的认识在不断提高。但各机构的评估方法一般只针对各自的天平校准,互相之间差异巨大。除此之外,在评估的具体细节中,仍有很多问题模糊不清,目前为止还没有全面系统的评估实例。这说明天平校准不确定度的评估与实现标准化还有很远的距离。
天平校准不确定度的评估要实现标准化有困难,一是由于各校准机构所应用的校准系统千差万别,而校准系统的不确定度是最终天平校准不确定度的重要组成部分。大多数方法都是将校准系统与其它各因素引入的不确定度一并展开评估,这导致了各结构的评估方法均只适用于各自的天平校准,无法通用；二则是天平校准的整个过程中误差源众多,层次关系复杂。在评估过程中,经常出现某些误差源引入的不确定度被重复计算或被忽略的情况。基于此2个主要问题,本文着眼于天平校准不确定度评估的标准化,将校准系统引入的不确定度单独进行评估。除此之外,为合理归纳各误差源引入的不确定度并体现其作用方式,将误差源头分成随机误差和系统误差2部分,并将其引入的不确定度归类为精度极限和偏差极限。
1 评估方法概述风洞天平的校准,误差来源众多。它主要的误差来源有几方面：(1）校准系统。主要是载荷发生装置、载荷传递装置因加工、安装引入的误差；(2）天平自身。一是天平的弹性元件存在滞后、蠕变和非线性等缺陷,二是应变计存在温漂、零漂和非线性等现象；(3）数据采集系统。数采系统受分辨率、噪声和热效应因素等的影响,会存在测量与控制误差；(4）数据处理方法。主要是天平校准载荷表的编制方法、天平公式的求解方法等引入的系统误差。天平校准不确定度的评估,需要从上述误差源出发,建立的评估方法应能够体现各误差源及其作用方式。
对于校准系统,其引入的不确定度将单独展开评估。对于天平自身、数采系统和数据处理方法等引入的不确定度,由于校准过程中各因素同时作用,且校准工作者能够得到的信息只有天平读数及其它校准数据,所以若单独评估各项,是非常困难的。比较实际的做法是有效利用校准数据,尤其是检验载荷的残差,它是各种误差综合作用的结果,适合用来表征除校准系统外其它误差源引入的不确定度。
为合理体现其它误差源头的作用方式,可基于检验载荷的残差,从精度极限和偏差极限2部分具体展开评估工作：关于精度极限,考察精度极限最直接有效的方式就是重复。即重复加载同一检验载荷,通过各次检验载荷残差的标准偏差进行表征；关于偏差极限,可取各次检验载荷的残差均值直接进行表征。
2 评估流程 2.1 校准系统的不确定度评估校准系统安装完毕后,由于安装误差的存在,作用于天平上的实际载荷是存在误差的,并且该误差是恒定的。在该安装状态下重复校准天平时,校准系统的不确定度,即实际载荷的不确定度,是最终天平校准不确定度的一部分。
校准系统的不确定度评估,首先需根据校准系统的工作方式,分析校准系统可能引入误差的输入量,并逐一评估各输入量的不确定度值。然后列出实际载荷与各输入量的函数关系,即载荷的数学模型。最后按照不确定度传播定律,计算得到实际载荷的不确定度。
2.1.1 分析输入量对于一般的天平校准系统,载荷来源是砝码或其它力发生装置,最终的输出量是天平上的实际载荷。在载荷传递过程中,实际载荷的具体值,会受到校准系统各输入量的误差影响。不同的天平校准系统工作方式各不相同,决定了其输入量存在差别,各机构需要针对各自的校准系统单独展开分析。
图 1所示为某高超声速风洞配套的BCS-100天平校准系统。被校准天平通过支杆连接至基准台上,通过基准台实现被校准天平的定位和调整。专门设计了加载头为天平提供各分量载荷的加载,安装时将加载头连接至天平上,后连接钢丝,钢丝经过滑轮连接砝码盘。校准时向砝码盘上施加砝码,用砝码的自重实现各个载荷分量的模拟。关于该校准系统的详细信息,可查阅参考文献[11]。
|
| 图 1 BCS-100校准系统的示意图 Fig. 1 Sketch of BCS-100 |
对于该天平校准系统,引入误差的输入量主要有天平安装的滚转角、加载头安装角、滑轮安装位置和加载头的加载点位置等,具体如表 1所示。关于天平线位移及各位置参数的正方向,与图 1所示坐标轴的正方向一致；各角度的正方向,与传统俯仰角、偏航角和滚转角的正方向定义一致。
| 输入量 | 代号 | 理论值 |
| 砝码值 | F0、F11、F12、F13、F14、F21、F22、F31、F32、F34 | 砝码标称值 |
| 天平线位移 | Xf 、Yf 、Zf | 实测值换算 |
| 天平角位移 | αf 、βf 、γf | 实测值换算 |
| 天平安装滚转角 | γtp | 0 |
| 加载头安装角 | αjzt、βjzt、γjzt | 0 |
| 滑轮安装位置 | WX0、WX31、WX32、WX34、WY21、WY22、WY31、WY32、WY34、WZ0、WZ21、WZ22 | 0 |
| WY0、WX21、WX22、 | ||
| WZ31、WZ32、WZ34 | 实测值 | |
| 加载头的加载点位置 | PX0、PX31、PX32、PX34、PY21、PY22、PY31、PY32、PY34、PZ0、PZ21、PZ22 | 0 |
针对校准系统的各输入量,可根据不确定度的A类或B类评定手段,逐一评估其不确定度值。
2.1.2 列出数学模型一般来说,校准系统的输入量很多,如何有效组织各输入量是建立数学模型的关键,这也是不确定度分析的难点。目前有些研究机构认识到单独评估校准系统不确定度的必要性[9],但还未见任何评估实例。本文提出从载荷来源的空间分解方式出发,逐一分析各输入量对实际载荷的作用方式并得到函数关系,最后汇总各载荷源,建立最终的数学模型。
实际载荷的数学模型,不等同于实际载荷测量结果的计算公式,即使有些因素对载荷结果的影响很小,但对于测量不确定度来说是必须考虑的。如校准系统存在理论值为0的各输入量Xi,但由于安装或工作过程中的其它原因,各输入量会存在误差并引入不确定度,必须将其误差的修正值δXi加入数学模型。
以BCS-100校准系统的阻力Q为例。首先分析载荷源G31对阻力Q的影响,图 2所示为砝码值F31在xz平面对Q的干扰。G31滑轮的x向位置WX31存在安装误差δWX31、加载头上的加载点位置PX31存在加工误差δPX31,在与天平x方向的线位移Xf共同作用下,砝码值F31会对Q产生干扰：
|
| 图 2 xz平面内砝码值F31对Q的干扰 Fig. 2 Component Q of weight F31 in xz plane |
当加载头存在偏航角的安装误差δβjzt时,在与天平的角位移βf共同作用下,式（1）变化为：
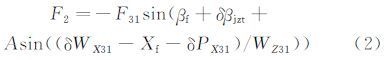
式（2）中F31的矢量方向在xz平面内。实际上,由于高度y方向的各输入量误差,F31不可能完全位于xz平面内。图 3所示为F31向xz平面上的投影示意图。滑轮G31的y向位置WY31存在安装误差δWY31、加载头上的加载点位置PY31存在加工误差δPY31,在与天平y方向的线位移Yf共同作用下,砝码值F31在xz平面上的投影可表示为：
|
| 图 3 砝码值F31向xz平面的投影 Fig. 3 Projection to xz plane of weight F31 |
当天平存在滚转角的安装误差δγtp,并且加载头存在滚转角的安装误差δγjzt时,在与天平的角位移γf共同作用下,式（3）变化为：
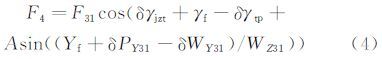
综合式（2）和（4）,得到载荷源G31与Q的函数关系为
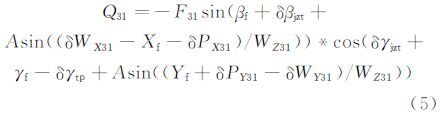
同理,可依次分析其它各载荷源对Q的影响方式,篇幅所限,不再叙述。汇总各载荷源,得到Q的数学模型为：
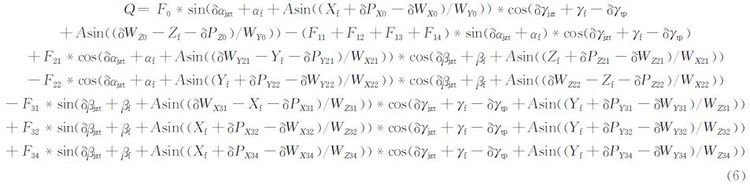
天平校准过程中加载了多组拟合载荷和检验载荷,各组载荷均有相应的不确定度结果。针对检验载荷组Fj,其中,j=1、2、…n,为检验载荷中的一组。设作用于天平上的实际载荷为Fj0,按照不确定度传播定律,可得到Fj0的合成标准不确定度为[12]：
式中: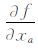
为输入量xa的灵敏系数,可根据数学模型计算得到；u(xa)为输入量xa的不确定度值；u(xa,xb)为输入量xa和xb之间的协方差。
式（7）只是其中一组检验载荷的结果,对各组检验载荷Fj的结果进行方根和处理,作为校准系统的不确定度结果。
天平自身、数采系统、数据处理等其它因素引入的不确定度,分成精度极限和偏差极限2部分展开评估。精度极限,是各随机误差引入的不确定度的综合；偏差极限,是各系统误差引入的不确定度的综合。在评估时应避免随机误差与系统误差混缠在一起,考察二者最直接有效的方式就是开展重复的天平校准。关于重复的方式,各次校准应单独加载拟合载荷和检验载荷,单独计算各次的天平公式和检验载荷残差。由于校准系统的安装误差引入的不确定度,已通过校准系统的不确定度得到了有效考察。所以,重复校准时不再拆装校准系统,保证同一安装状态。
重复开展N次天平校准后,直接取各次天平校准的检验载荷残差均值,表征偏差极限；计算各次天平校准的检验载荷残差的标准差,处理后表征精度极限。此时得到的偏差极限体现了天平自身、数据处理方法共同引入的系统误差；得到的精度极限则体现了除校准系统之外全部流程引入的随机误差。二者的具体计算流程如下：
2.2.1 偏差极限天平在各次校准完成后,依次拟合得到天平公式[Ci],其中,i为重复校准的次数；加载检验载荷可得到天平读数[Rij],计算反算检验载荷Fij为：
计算各次校准的反算检验载荷Fij与实际载荷Fj0的残差,残差结果为：
针对N次重复的天平校准,可得到残差εij的均值,作为该组检验载荷的偏差极限估值。
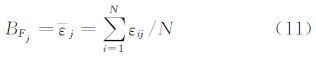
对各组检验载荷的偏差极限估值进行方根和处理,作为校准的偏差极限结果。
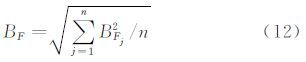
针对各检验载荷组Fj,计算N次重复校准时残差εij的标准差,即
由于选取N次校准残差的均值ε—j作为测量结果,取安全因子k=2,得到该组检验载荷精度极限的估值为：
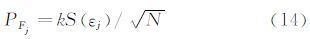
对各组检验载荷的精度极限估值进行方根和处理,作为校准的精度极限结果。
评估得到校准系统的不确定度,并通过偏差极限和精度极限得到其它误差源引入的不确定度后,对三者进行合并,作为最终的校准不确定度结果。
基于BCS-100校准系统,选择某高超声速风洞的应变天平TG624C,运用上述方法开展了7次重复校准。图 4所示为各载荷单元在各次天平校准中的检验载荷残差数据。
|
| 图 4 各次天平校准检验载荷的残差 Fig. 4 Residuals of checking loads in each calibration |
运用上述的评估方法,首先评估得到校准系统的不确定度,并额外计算了校准系统的各不确定度分量,及各不确定度分量在校准系统不确定度中的所占比重。表 2列出了3个力分量的相关结果。
| 输入量 | Q/kg | Y/kg | Z/kg | |||
| 不确定度分量 | 比重 | 不确定度分量 | 比重 | 不确定度分量 | 比重 | |
| Fi | ≈0 | 0 | ≈0 | 0 | ≈0 | 0 |
| PXi PYi PZi | ≈0 | 0 | ≈0 | 0 | ≈0 | 0 |
| αjzt | 0.0068 | 19.3% | 0.0010 | 1% | ≈0 | 0 |
| βjzt | 0.0066 | 18.3% | ≈0 | 0 | 0.0049 | 1.2% |
| γjzt | ≈0 | 0 | 0.0014 | 1.7% | 0.0068 | 2.2% |
| γtp | ≈0 | 0 | 0.0085 | 67.1% | 0.0427 | 87.9% |
| αf | 0.0115 | 55.4% | 0.0016 | 2.5% | ≈0 | 0 |
| βf | 0.0023 | 2.3% | ≈0 | 0 | 0.0014 | 0.1% |
| γf | ≈0 | 0 | 0.0022 | 4.5% | 0.0111 | 6.0% |
| Xf | ≈0 | 0 | ≈0 | 0 | ≈0 | 0 |
| Yf | ≈0 | 0 | 0.0048 | 21.6% | ≈0 | 0 |
| Zf | ≈0 | 0 | ≈0 | 0 | 0.0065 | 2.1% |
| WX0 | 0.0031 | 4.1% | ≈0 | 0 | ≈0 | 0 |
| WZ0 | ≈0 | 0 | ≈0 | 0 | 0.0031 | 0.5% |
| WY21 | ≈0 | 0 | 0.0005 | 0.2% | ≈0 | 0 |
| WZ21 | ≈0 | 0 | ≈0 | 0 | 0.0005 | 0 |
| WY22 | ≈0 | 0 | 0.0005 | 0.2% | ≈0 | 0 |
| WZ22 | ≈0 | 0 | ≈0 | 0 | 0.0005 | 0 |
| WX31 | 0.0009 | 0.4% | ≈0 | 0 | ≈0 | 0 |
| WY31 | ≈0 | 0 | 0.0009 | 0.8% | ≈0 | 0 |
| WX32 | 0.0004 | 0.1% | ≈0 | 0 | ≈0 | 0 |
| WY32 | ≈0 | 0 | 0.0004 | 0.2% | ≈0 | 0 |
| WX34 | 0.0004 | 0.1% | ≈0 | 0 | ≈0 | 0 |
| WY34 | ≈0 | 0 | 0.0004 | 0.2% | ≈0 | 0 |
| WY0 WX21 | ||||||
| WX22 WZ31 | ≈0 | 0 | ≈0 | 0 | ≈0 | 0 |
| WZ32 | WZ34 | |||||
通过表 2的数据结果可以看出,只有个别输入量引入的不确定度占绝对优势,其余大部分不确定度分量非常小。总体上讲,天平安装的滚转角和加载时天平的角位移,二者引入的不确定度为主要分量,应作为该校准系统技术改造的重点；加载头的加载点位置和砝码引入的不确定度相比之下非常小,可以忽略不计。
通过与滑轮相关的不确定度比重可以发现：总体上滑轮引入的不确定度很小,并且产生载荷的生力滑轮,不确定度分量基本为0,相比之下其它滑轮的干扰引入的不确定度稍大。以阻力Q为例,阻力Q靠G21和G22产生阻力,但G21和G22引入的不确定度基本为0,滑轮G31、G32、G34沿X向的偏移会产生额外的阻力分量,其引入的不确定度则相对要大很多。
3.2 综合评估结果表 3所示为该天平的校准载荷及校准不确定度的综合评估结果。
| My/(kg·m) | Z/kg | Mz/(kg·m) | Y/kg | Mx/(kg·m) | Q/kg | |
| 校准载荷 | 1.04 | 12 | 2.6 | 80 | 0.64 | 12 |
| 校准系统的不确定度 | 0.0022 | 0.0455 | 0.0006 | 0.0104 | 0 | 0.0154 |
| 其它误差引入 偏差极限 | 0.0004 | 0.0230 | 0.0020 | 0.0657 | 0.0022 | 0.0155 |
| 的不确定度 精度极限 | 0.0004 | 0.0072 | 0.0015 | 0.0140 | 0.0005 | 0.0056 |
| 不确定度结果 | 0.0023 | 0.0515 | 0.0026 | 0.0680 | 0.0023 | 0.0226 |
| 不确定度相对值（‰） | 2.2 | 4.3 | 1.0 | 0.8 | 3.6 | 1.9 |
通过表 3的数据结果可以看出：Y和Mz的不确定度的相对值较小,Q、Z和My3个单元的不确定度相对较大。这归结于Y和Mz作为大量,其它载荷分量对其造成的干扰,相对其本身很小；而Q、Z和My3个单元的不确定度来源主要是Y和Mz2个大量的干扰,这由表 2中Q、Z的各不确定度分量也可以得到验证。对于阻力Q,由于加载头俯仰角αjzt和天平角位移αf的存在,使法向力Y在阻力Q上产生投影,是Q主要的不确定度来源；对于侧力Z,天平滚转角γtp的存在,使Y在Z上产生投影,是Z的主要不确定度来源。
除此之外,通过表 3可见精度极限相比于偏差极限要小很多,即该校准系统的安装状态固定后,天平校准不确定度的主要来源,是由天平校准各环节的系统误差引入。
4 方法讨论本文天平校准不确定度的评估方法,单独评估校准系统的不确定度,使得整套方法对于其它校准系统也可通用,这使实现天平校准不确定度的评估标准化变为可能。除此之外,对于校准系统之外的各误差源引入的不确定度,采用精度极限和偏差极限的分类方式,可以直接看出随机误差与系统误差的作用方式及比重结果。该分类方式在风洞试验的不确定度评估中曾有过应用[2],对于处理复杂系统,该方法效果良好。
本文基于检验载荷评估了校准系统的不确定,并基于检验载荷评估了精度极限和偏差极限,所以该方法是基于检验载荷得到的。当检验载荷的载荷值及组数发生变化时,校准不确定度的数值结果也会发生变化。由于校准不确定度的评估,其中的目的之一是给风洞试验的不确定度评估提供数据[2]。所以,为使评估结果更具有实际意义,应使检验载荷水平尽量接近风洞试验载荷。
本文暂时未单独计算数据采集系统和滑轮摩擦力引入的不确定度。二者引入的精度极限,都包括在最终的精度极限中。采集系统引入的偏差极限,对于天平校准来说,主要是量程误差和截断误差2个因素,基于应用同样采集系统的风洞试验不确定度的评估经验,发现其偏差极限很小,可以忽略；滑轮摩擦力引入的偏差极限,以BCS-100校准系统为例,目前还未能实现定量评估,该工作将在后续进行。
本文暂时未给出校准不确定度的自由度,一方面在于评估实际载荷的不确定度时,校准系统很多输入量的不确定度评估是基于B类评定手段,在计算自由度时存在困难；另一方面,本文的评估方法整体上基于检验载荷的残差,并非直接根据测量手段获得,从原则上讲自由度的概念变得牵强,必要性不大。
5 结 论各机构的校准系统工作方式不同,决定了校准系统的输入量互不相同,但本文的分析方法是通用的。研究工作可得到如下主要结论：
(1）单独评估校准系统的不确定度,使评估方法实现通用变为可能；采用精度极限和偏差极限的分类方式,对于复杂系统的不确定度评估,效果良好。
(2）对BCS-100天平校准系统的TG624C天平进行评估,结果表明：天平安装的滚转角和加载时天平的角位移,是校准系统最大的不确定度分量；天平的大量Y和Mz的校准不确定度相对较小,Q、Z和My 3个单元受Y和Mz这2个大量的干扰,不确定度相对稍大；校准各环节的系统误差是不确定度的主要来源。
(3）本文提出的天平校准不确定度的评估方法,其它校准机构也可应用,对天平校准不确定度评估的标准化工作具有广泛的参考意义。
| [1] | Belter D L. Comparison of wind tunnel data repeatability with uncertainty analysis estimates[R]. AIAA-98-2714, 1998. |
| [2] | Anon. Assessment of wind tunnel data uncertainty[R]. AIAA-S-071-1995, 1995. |
| [3] | Mark E Kammeyer, Mathew L Rueger. Estimation of the uncertainty in internal balance calibration through comprehensive error propagation[R]. AIAA-2008-4029. |
| [4] | John S Tripp. Strain gauge balance uncertainty analysis at NASA Langley-a technical review[R]. AIAA-94-2589, 1999. |
| [5] | Maria L C C Reis, Olympio A F. A method for estimation of the calibration uncertainty of an external six-component wind tunnel balance[R]. AIAA-2002-2793. |
| [6] | Maria L C C Reis, Olympio A F. Calibration uncertainty of an external six-component wind tunnel balance[R]. AIAA-2003-3884. |
| [7] | 中国人民解放军总装备部. 风洞应变天平规范[S]. GJB 2244A-2011, 2011. |
| [8] | Berng Ewald. The uncertainty of internal wind tunnel blalances: definition and verification[C]. The Third International Symposium on Strain-Gauge Balances, Darmstadt, 2002. |
| [9] | R Bergmann, I Philipsen. Some contemplations on a proposed definition of uncertainty for balances[R]. AIAA-2010-4546. |
| [10] | David Cahill. Balance Calibration Uncertainty Introduction to Discussion Standardization[C]. 6th International Symposium on Strain-Gage Balances, 2008. |
| [11] | Xiong Lin, Gong Jian. A research on calibration method of obtaining body fixed coordinate system coefficients matrix using non-repositioning calibration system[C]. 9th International Symposium on Strain-Gage Balances, 2014. |
| [12] | 中国人民解放军总装备部. 测量不确定度的表示及评定[S]. GJB 3756-99, 1999. |