乘波体的概念自1959年被Nonweiler[1]提出以来,经过几十年的研究,已经发展出多种乘波体设计方法,其中较为经典的是Rasmussen[2, 3]等人提出的锥导乘波体设计方法和Sobieczky[4, 5]提出的吻切锥乘波体设计方法。但对于以吸气式超燃冲压发动机为动力的高超声速飞行器来说,基于传统乘波体设计方法设计的乘波体对来流气体的压缩量不足,不能满足进气道内收缩段入口对气流参数的要求[6]。国内外都已针对这一问题开展了研究,已经经过飞行演示验证的X-51A[7]采用了两级压缩。刘嘉[8]、王发民等[9]提出了用相交楔锥流场构造乘波构型飞行器前体的方法,该方法属于乘波体设计中的生成体法,利用该方法可以生成两级压缩乘波体,但改变 设计条件 需要重新计算生成体--楔锥流场。贺旭照[6]发展 了一种密切曲面锥(Osculating Curved Cone,OCC)乘波体设计方法,该乘波体前部分采用传统的直锥乘波体设计方法,通过第一道激波对来流压缩;后接曲面锥等熵压缩段,通过压缩马赫波继续进行压缩;再接直线过渡段。该型乘波体克服了传统乘波体压缩量不足和容积率小的缺点。
同样为了解决乘波体压缩量不足的问题,本文在吻切锥理论的基础上,给出一种多级压缩乘波体的设计方法,该方法属于乘波体设计方法中的指定激波法,通过多道激波对气流进行压缩,相比于马赫波压缩,具有直接高效的特点。给定一定的设计条件,依据发展的设计方法设计得到一个三级压缩锥导乘波体构型,对比分析其在无粘条件和粘性条件下的性能。并对该乘波前体与二元进气道连接的构型进行风洞试验研究。
1 三级压缩锥导乘波体设计 1.1 设计方法多级压缩乘波体的设计预期是由该乘波体产生的多道激波相交于乘波体底部截面内,如图 1所示,以三级压缩乘波体为例,3道激波相对于来流的激波角分别为β1、β2和β3,3道锥形激波交于图 1中底部截面的圆上。
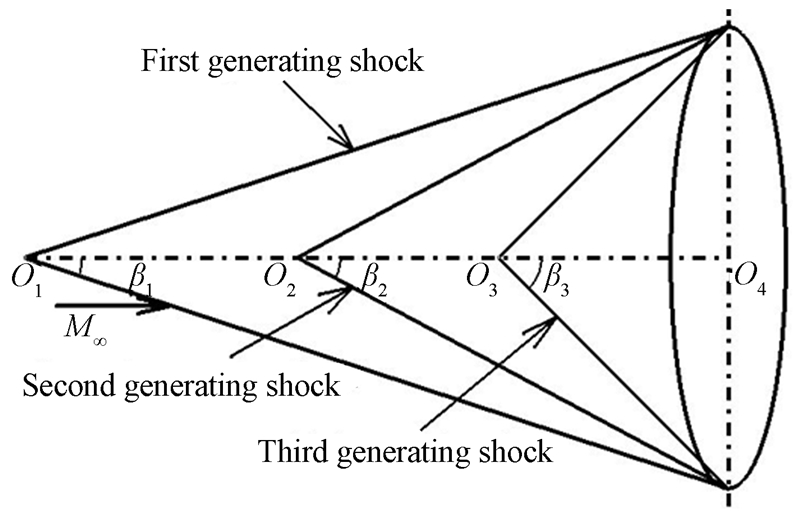 |
| 图 1 锥形激波结构的设计预期 Fig 1 Design expectation of conical shock wave shape |
在多级压缩乘波体设计方法中,基准流场采用的均是Taylor-Maccoll流动,即零迎角圆锥绕流。多级压缩乘波体的第一级依然和传统乘波体设计方法一样在零迎角圆锥绕流基准流场中进行流线追踪,当流线追踪至图 2中第二道激波面时,流动与来流方向存在迎角α1,对于图中虚线表示的原锥形激波面来讲,这种情况下不可以用零迎角圆锥绕流来构造第二级压缩基准流场。
 |
| 图 2 二级压缩基准流场构造示意图 Fig 2 Schematic diagram of generating cone for second-stage compression |
多级压缩乘波体设计方法主要解决的问题就是第二级以及后面级基准流场的构造问题。为了解决二级压缩基准流场的构造问题,根据Sobieczky[4]提出的吻切锥理论对二级压缩基准流场进行了重构。吻切锥理论[4]指出:一般三维超声速流运动方程都可以在二阶精度范围内用一个轴对称流的运动方程来逼近。
参考吻切锥原理,将图 2中的中轴线O2O3绕O2沿图示方向旋转α1,使新得到的轴线O2O4与A点的流动方向平行,即用一个轴线与A点流动方向平行的零迎角圆锥绕流逼近A点的流动参数,使零迎角圆锥绕流的来流参数与A点的流动参数相同,用新得到的基准流场描述A点处的激波和激波后的流动。
经过这样处理后得到新的锥形激波面和生成锥可以用Taylor-Maccoll流动来构造基准流场,其二级压缩的实际激波角为β2-α1。第三级压缩的基准流场采用同样的方法进行处理,如图 3所示,B点的流动相对于轴线O2O5存在迎角α2,经过上述处理后,新的三级压缩实际激波角为β3-α1-α2。
 |
| 图 3 三级压缩基准流场构造示意图 Fig 3 Schematic diagram of generating cone for third-stage compression |
三级压缩锥导乘波体设计流程为:首先从前缘离散点出发,在一级压缩基准流场中流线追踪至二级激波面;计算流线与二级激波面交点处流动相对于二级锥形激波轴线的迎角,进行上述处理得到新的零迎角圆锥绕流流场;在新的锥形流场中继续流线追踪至三级激波面,进行与二级相同的处理后继续流线追踪至指定长度。最终获得如图 4所示的某吻切平面内的三级压缩乘波体形状和激波结构。
 |
| 图 4 吻切平面内流线及激波示意图 Fig 4 Schematic diagram of streamline and shock waves in osculating plane |
至此得到一个吻切平面内的三级压缩的三段基准流场以及该吻切平面内的流线。在多级压缩锥导乘波体设计方法中,不同的吻切平面中只有第一级压缩基准流场是同一个流场,后面级的基准流场根据流线与激波面的交点处的流动参数确定,类似于吻切锥乘波体设计中各吻切平面内的基准流场均不相同。本文各吻切平面内的二级和三级基准流场只用于描述当前吻切平面内的流动,当计算另一个吻切平面内的流线时需要重新计算二三级基准流场。在获得所有吻切平面内的流线后,通过建模软件即可得到其三维外形。
Taylor-Maccoll流动精确解的计算域是从激波后开始至锥面为止的扇形区域,在计算域内其有一个特征是由锥顶点发出的射线上流动参数是相等的,常规乘波体设计中采用的Taylor-Maccoll流动其激波前流动也是相等的,紧靠激波后参数由波前参数通过斜激波关系式计算得到。而本文图 2中的二级压缩基准流场激波前面沿激波上的流动参数是处处不相等的,其激波后流动是否还能够满足或者近似满足Taylor-Maccoll流动将决定多级压缩乘波体设计方法的合理性。由于目前尚没有发展出相应的理论来证明,并且数值模拟无法给出处处不同的来流条件,本文只能通过先设计得到多级压缩乘波体,再由多级压缩乘波体的流场反过来验证这一点。
1.2 三级压缩锥导乘波体根据多级压缩乘波体设计方法编写设计程序。设计程序实现了多级压缩乘波体的生成、计算网格的自动生成以及通过各基准流场的 Taylor-Maccoll流动计算设计预期流场。给定三级压缩锥导乘波体的设计条件为来流马赫数6.0;压强1197Pa;温度226.5K; 密度0.01841kg/m3;三级压缩激波角分别为11.315°、16.033°和22.155°;乘波体长度为16m。给定乘波体的前缘,上表面取来流自由流面时,设计得到的三级压缩锥导乘波体(WR3),如图 5所示。
 |
| 图 5 三级压缩锥导乘波体 Fig 5 Three-stage compression cone-derived waverider |
由于设计过程是基于无粘条件进行的,因此通过CFL3d对图 5所示三级压缩锥导乘波体在设计条件下的无粘数值模拟结果来验证设计方法,并与设计程序通过求解Taylor-Maccoll流动得到的流场进行对比。设计程序计算得到的流场是按照设计预期来求解的,并不是真实的流场,而是设计方法预期达到的流场。在设计程序中通过代数生成法生成了多级压缩乘波体的计算网格,各网格点的流动参数不是由数值模拟方法或者特征线方法计算得到,而是根据网格点所处的位置计算该点的流动参数,若网格点位于第一道激波前或上表面则直接赋为来流参数;若网格点位于一级压缩区域内则通过求解一级压缩Taylor-Maccoll流动得到该点的流动参数;若网格点位于二级压缩区域内则通过求解图 2中二级压缩Taylor-Maccoll流动得到该点的流动参数,以此类推得到整个流场。图 6对比了由设计程序和CFL3d分别计算得到的对称面所在吻切平面内的马赫数等值线,2幅图中所取的马赫数尺度相同。
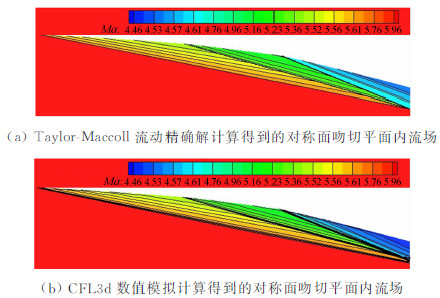 |
| 图 6 设计程序与数值模拟得到的流场对比 Fig 6 Comparison of flow field obtained by design code and numerical simulation |
由对称面内的流场可以看出,理论解中激波是没有厚度的,多条马赫数等值线聚合在一起,3道激波按照设计预期精确地相交于一点。在实际数值解中,受网格和计算精度的制约,这种理想化的激波结构是无法达到的,但数值模拟流场还是与设计程序计算得到的流场具有高度的一致性。虽然激波前面沿激波的来流流动参数是不相等的,但经过激波压缩后,激波后的流动参数又归为相等,而Taylor-Maccoll流动正是要求激波后面沿激波的流动参数相等。因此经过数值模拟流场与设计程序得到的理论流场进行对比后,可以认为按图 2倾转圆锥方式处理后的流场是满足或者说是高度近似于满足Taylor-Maccoll流动。其他吻切平面内流场与对称面内的流场结构相同,参考吻切锥原理,用零迎角圆锥绕流流动(Taylor-Maccoll流动)在二阶精度范围内逼近当前吻切平面激波后的流动在多级压缩乘波体设计方法中是可行的。
图 7为该乘波体在无粘条件下的激波结构图,图中各截面内的激波形状均为圆弧状,3道激波为图 1所示锥面激波中的一部分,并且相交于乘波体底部截面。数值模拟结果与设计预期吻合,说明了多级压缩乘波体设计方法是可行的。
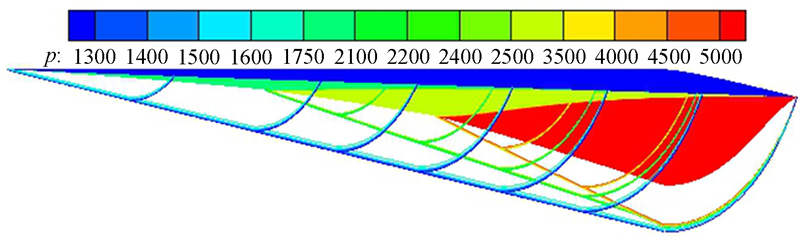 |
| 图 7 无粘条件下三级压缩锥导乘波体激波结构 Fig 7 The shock wave shape of three-stage compression cone-derived waverider under inviscid condition |
同时需要对设计得到的三级压缩锥导乘波体的压缩性能进行一定的分析。流量系数、总压恢复系数、压缩后马赫数和压比p/p∞是评价乘波体压缩性能的重要参数。压缩后的参数均是底部截面内激波与乘波体之间的面积平均参数,流量系数σ代表了气流到达进气道进口处的质量通量的相对变化率,表达式为σ=ρu/(ρu)∞[8]。总压恢复系数η=p02/p01为压缩后的总压与来流总压的比值,它反映了气流经过前体后的能量损失。为了说明三级压缩锥导乘波体的压缩能力,在相同设计条件下分别设计得到了如图 8所示的传统单级锥导乘波体(WR1)及二级压缩锥导乘波体(WR2)。
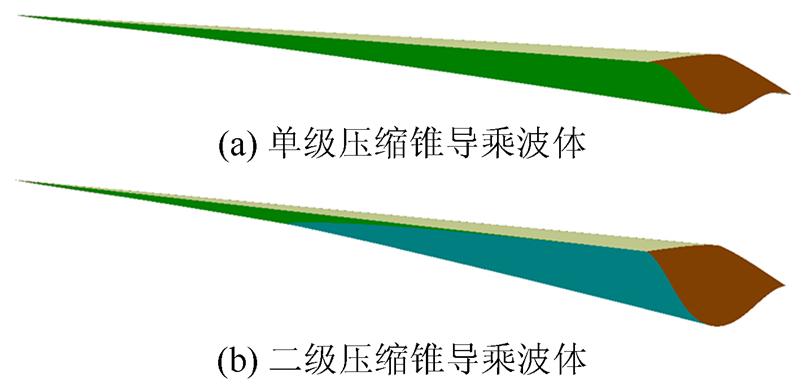 |
| 图 8 单级与二级压缩锥导乘波体 Fig 8 Single stage and two-stage compression cone-derived waverider |
对生成的单级和二级压缩锥导乘波体进行了无粘设计条件下的数值模拟,分别计算了3种锥导乘波体底部截面内激波与乘波体之间区域的压缩参数,如表 1所示。由表中数据可知,三级压缩锥导乘波体的流量系数由传统单级乘波体的1.38提升至2.73,压缩后马赫数有了明显的降低,压比提升至4.6,表明了多级压缩乘波体有效解决了传统乘波体压缩量不足的问题。本文中二三级激波角取值较小,取较大的二三级激波角可以获得更大的流量系数。
| WR1 | WR2 | WR3 | |
| 流量系数 | 1.38 | 1.80 | 2.73 |
| 总压恢复系数 | 99.36% | 98.74% | 95.49% |
| 压缩后马赫数 | 5.55 | 5.19 | 4.64 |
| 压比 | 1.60 | 2.39 | 4.61 |
同时对三级压缩锥导乘波体进行了粘性条件下的数值模拟分析,表 2给出了该乘波体在有粘和无粘条件下的升阻力数据,参考面积取三级压缩锥导乘波体下表面面积。由于粘性的存在,相比于无粘条件升阻比下降了14.7%,升力下降了0.87%,导致升阻比下降的主要原因是考虑粘性后阻力增加了16.16%。
| C L | C D | L/D | |
| Inviscid | 0.08022 | 0.02252 | 3.562 |
| Viscous | 0.07952 | 0.02616 | 3.040 |
考虑粘性后,在前缘位置出现了小量的溢流现象,如图 9所示。图中激波结构与无粘条件下相比没有太大的变化,只在粘性边界层作用下各级压缩角均有所增大,使底部截面的三道激波相距一段很小的距离。
 |
| 图 9 粘性条件下三级压缩锥导乘波体激波结构 Fig 9 The shock wave shape of three-stage compression cone-derived waverider under viscous condition |
图 10给出了三级压缩锥导乘波体在无粘和粘性条件下底部截面密度云图的对比图。图中由粘性产生的边界层将激波和激波内的流动向下移动了一定的距离,移动的距离约为边界层的厚度,并在前缘处出现了一些溢流。边界层对多级压缩乘波体产生的激波的影响机理相当于边界层的存在增加了乘波体的厚度,从而增加了激波角,使整体流动向下移动。在对多级压缩乘波体的研究过程中发现,激波对边界层厚度同样具有压缩作用,在多级压缩乘波体第二级及后面级产生激波的位置,激波后的边界层厚度会降低。图 10底部截面上经过第二级和第三级激波压缩后的边界层厚度要比相同流程的平板边界层厚度小,这保证了多级压缩乘波体由于边界层产生的升力损失比传统乘波体小。
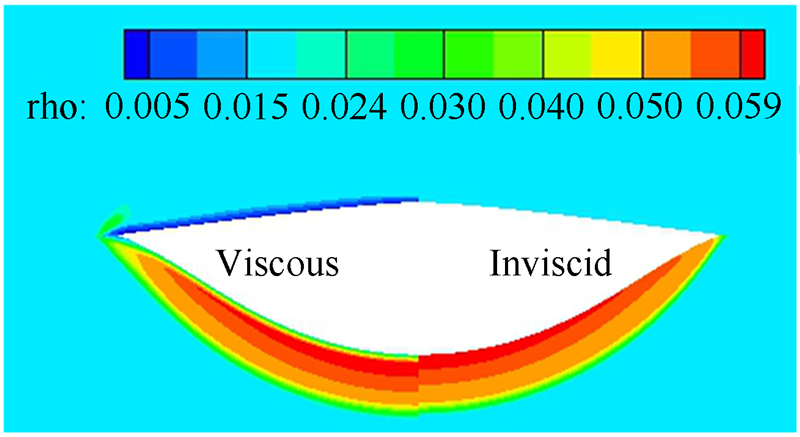 |
| 图 10 有粘和无粘条件下底部截面流场密度对比 Fig 10 Viscous and inviscid density contour comparison at bottom section |
升阻力数据的对比结果、激波结构以及底部截面流场对比结果表明,经过多级压缩乘波体设计方法设计出来的乘波体在粘性条件下依然具有良好的乘波特性。
3 高超声速风洞校核实验上表面采用自由流面的乘波体具有尖锐的前缘,在前缘处造成严重的气动加热问题[12, 13, 14],并存在容积率低的缺点,且不便于风洞实验模型加工,因此在应用乘波体时,采用膨胀式上表面。为了在风洞实验中标明激波交汇的位置,在三级压缩锥导乘波体后加了一段进气道,进气道唇口按照波系贴口原理取底部截面上3道激波交汇圆弧的一段,进气道用于观察3道激波能否交于唇口从而通过实验验证设计方法。由此获得了进行风洞实验的三级压缩锥导乘波体前体/进气道布局,如图 11所示。
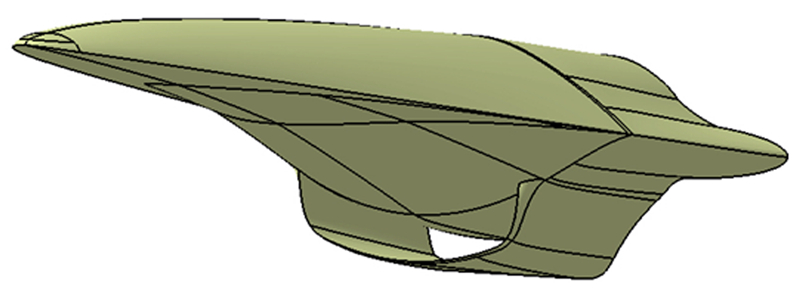 |
| 图 11 三级压缩锥导乘波体前体/进气道 Fig 11 The three-stage compression cone-derived waverider forbady and inlet configuration |
数值模拟和风洞实验相互验证[10, 11]是研究高超声速飞行器气动布局的一个有效手段。本文对发展的设计方法进行了高超声速风洞实验,在波系结构方面与数值模拟结果进行了对比校验。风洞实验所使用的缩比实体模型如图 12所示,模型材料为HP20钢,采用数控铣磨加工成型。模型长236mm,宽135mm,厚度为50mm,缩比为1∶85。
 |
| 图 12 风洞试验模型的上下表面 Fig 12 Upper and lower surface of wind tunnel test model |
风洞实验设备为南京航空航天大学高超声速风洞(NHW),实验段喷管出口直径为500mm,名义实验马赫数范围为5.0~8.0,模拟飞行高度为27~59km。图 13为马赫数5.752、总压0.2856MPa、总温563K条件下,迎角4.0127°时的流场纹影图与数值模拟流场图。图 14为该构型在马赫数4.975、总压0.3465MPa、总温546K条件下,迎角为4.3203°时的流场纹影图与数值模拟流场图。
 |
| 图 13 马赫数5.752,总压0.2856MPa,总温563K条件下,迎角为4.0127°时的流场纹影图与流场 Fig 13 Shadow graph map and flowfield at Ma5.752, total pressure 0.2856MPa, total temperature 563K, angle of attack 4.0127° |
 |
| 图 14 马赫数4.975,总压0.3465MPa,总温546K条件下,迎角为4.3203°时的流场纹影图与流场 Fig 14 Shadow graph map and flowfield at Ma4.975, total pressure 0.3465MPa, total temperature 546K, angle of attack 4.3203° |
从风洞实验纹影图来看,3道激波都能够相交于进气道唇口附近。无粘设计时设计迎角为0°,考虑粘性后,激波由于边界层的存在会向下偏移,使激波偏离了进气道唇口,实验时给定4°左右的迎角使激波向进气道唇口靠近。实验结果表明,在实际应用多级压缩乘波体时可以给定一定的迎角以消除激波偏离进气道唇口的问题。
由于第二道激波实际压缩转折角偏小,并且3道激波均为三维锥面激波,二三级激波分别包裹在前面的激波内,造成第二道激波在流场纹影图中并不能很好地分辨出。这一点也可以从数值模拟的流场图中看出,在流场密度云图中第二道激波由于其壁面转折角偏小而并不明显。
由于受风洞实验设备和观测手段的限制,只能从纹影图中看到对称面的激波结构。从数值计算和风洞实验的对比结果来看,2者对称面内流场相吻合,在风洞实验中该三级压缩锥导乘波体能够产生3道激波,并且激波能够和数值模拟结果一样相交于进气道唇口。通过风洞实验验证了本文多级压缩乘波体的设计预期是能够实现的,同时也表明了设计方法的可行性。
实验纹影和数值模拟图中膨胀式上表面对来流先压缩后膨胀,能够降低除头部一段区域外的上表面所受到的压力,进一步提升升力。采用膨胀式上表面后,对称面附近截面内还是可以保持激波附体的,但越往两侧,激波会出现脱体,使乘波特性减弱。虽然前缘钝化及膨胀式上表面使激波脱体的现象无法避免,但可以通过上表面的优化设计使脱体程度降到最低,这方面的工作还需进一步的研究。
4 结论三级压缩锥导乘波体的数值和实验研究结果表明:
(1) 参考吻切锥原理,用倾转圆锥绕流在二阶精度内逼近多级压缩激波后的流场的方法在多级压缩乘波体设计中是可行的。
(2) 设计状态下无粘数值模拟结果与理论设计预期相符,风洞实验与数值计算得到的流场吻合,数值模拟验证了多级压缩乘波体设计方法的正确性,风洞实验验证了对称面内的激波结构是满足设计预期及数值模拟结果的,从侧面间接证明了设计方法的可行性。
(3) 相较于相同设计条件下的传统单级压缩乘波体,三级压缩锥导乘波体的流量系数提升了97.8%,压缩后马赫数由5.55降低至4.64,压比由1.60提升至4.61,由于一级激波角受到飞行器整体尺寸的限制,不能随意改动,但二三级激波角不会受到这方面的限制,给定更大的二三级激波角,可以获得更大的流量系数,实际应用时根据具体的进气道要求进行设计。通过多级压缩乘波体设计方法设计得到的乘波体对来流进行多次激波压缩,可有效解决传统乘波体压缩量不足的问题。
(4) 文中以三级压缩锥导乘波体验证多级压缩乘波体设计方法,实际应用时,该方法可以生成任意压缩级数的乘波体,并可以应用到锥导和吻切锥乘波体中。 由设计方法设计得到的乘波体在数值模拟和风洞实验方面进行了验证,但在多级压缩乘波设计方法可靠性的理论证明方面还有所欠缺,后期将对这方面展开研究,使多级压缩乘波体设计方法更加完备。为了更进一步研究多级压缩乘波体,后期考虑在原实验模型的基础上进行测压实验,测出其下表面的压力分布与数值结果进行对比。并开展以多级压缩乘波体为前体的高超声速飞行器整体气动布局设计与性能分析。
| [1] | Nonweiler T R F. Aerodynamic problems of manned space vehicles[J]. Journal of Royal Aeronautical Society, 1959, 63: 512-528. |
| [2] | Rasmussen M L, Jischke M C, Daniel D C. Experimental forces and moments on cone-derived waveriders for M∞=3 to 5[J]. Journal of Spacecraft and Rockets, 1982, 19(6): 592-598. |
| [3] | Rasmussen M L, Jischke M C, Daniel D C. Waverider configurations derived from inclined circular and elliptic cones[J]. Journal of Spacecraft and Rockets, 1980, 17(6): 537-545. |
| [4] | Sobieczky H, Dougherty F C, Jones K D. Hypersonic waverider design from given shock waves[C]. First International Waverider Symposium, University of Maryland, 1990. |
| [5] | Jones K D, Sobieczky H, Seebass A R, et al. Waverider design for generalized shock geometries[J]. Journal of Spacecraft and Rockets, 1995, 32(6): 957-963. |
| [6] | 贺旭照, 倪鸿礼. 密切曲面锥乘波体-设计方法与性能分析[J]. 力学学报, 2011, 43(6): 1077-1082. He Xuzhao, Ni Hongli. Osculating inward turning cone: design methods and performance analysis[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(6): 1077-1082. |
| [7] | Matthew P B, Steven P S. Effect of freestream noise on roughness-induced transition for the X-51A forebody[J]. Journal of Spacecraft and Rockets, 2008, 45(6): 1106-1116. |
| [8] | 刘嘉, 王发民. 乘波前体构型设计与压缩性能分析[J]. 工程力学, 2003, 20(6): 130-134. Liu Jia, Wang Famin. Waverider configuration design and forebody compressibility analysis[J]. Engineering Mechanics, 2003, 20(6): 130-134. |
| [9] | 王发民, 李立伟, 姚文秀, 等. 乘波飞行器构型方法研究[J]. 力学学报, 2004, 36(5): 513-519. Wang Famin, Li Liwei, Yao Wenxiu, et al. Research on waverider configuration method[J]. Acta Mechanica Sinica, 2004, 36(5): 513-519. |
| [10] | 贺旭照, 周正, 毛鹏飞, 等. 密切曲面内锥乘波前体进气道设计和试验研究[J]. 实验流体力学, 2014, 28(3): 39-44. He Xuzhao, Zhou Zheng, Mao Pengfei, et al. Design and experimental study of osculating inward turning cone waverider/inlet (OICWI)[J]. Journal of Experiments in Fluid Mechanics, 2014, 28 (3): 39-44. |
| [11] | 贺元元, 乐嘉陵, 倪鸿礼. 吸气式高超声速机体/推进一体化飞行器数值和试验研究[J]. 实验流体力学, 2007, 21(2): 29-34. He Yuanyuan, Le jialing, Ni Hongli. Numerical and experimental study of airbreathing hyoersonic airframe/propulsion integrative vehicle[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(2): 29-34. |
| [12] | 李晓宇, 欧海英, 李洪伟, 等. 钝前缘乘波体气动特性研究[J]. 弹箭与制导学报, 2010, 30(3): 122-124. Li Xiaoyu, Ou Haiying, Li Hongwei, et al. Aerodynamic performance of waveriders with blunt edges[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(3): 122-124. |
| [13] | 徐大军, 蔡国飙, 乐川. 吸气式高超声速飞行器气动热试验研究[J]. 宇航学报, 2006, 27(5): 1004-1009. Xu Dajun, Cai Guobiao, Yue Chan. Aeroheating experiment for airbreathing hypersonic vehicle[J]. Journal of Astronautics, 2006, 27(5): 1004-1009. |
| [14] | 刘建霞, 尘军, 侯中喜, 等. 一种乘波构型边缘钝化方法的仿真与试验研究[J]. 空气动力学学报, 2014, 32(2): 171-176. Liu Jianxia, Chen Jun, Hou Zhongxi, et al. Numerical and experimental study of one blunt method for waverider configuration[J]. ACTA Aerodynamica Sinica, 2014, 32(2): 171-176. |
| [15] | 肖虹, 高超, 党云卿. 乘波体构型飞行器的高超声速测压实验研究[J]. 实验流体力学, 2011, 25(3): 34-36. Xiao Hong, Gao Chao, Dang Yunqing. Experimental study on aerodynamic characteristics of a hypersonic waverider configuration[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(3): 34-36. |



