0 引言

为了解决前向散射累积效应很强时Born近似失效的问题，Wu^[1]提出了实现De Wolf近似的两种方法：薄板近似和屏近似。薄板近似是将整个模型在垂直方向上划分成若干个薄板，采用De wolf近似对总波场不断更新，并在每一步内计算一次向后散射波场。薄板近似法可以称为广义广角相位屏法，但是薄板的散射效应与局部规则相位屏效应不同，因为前者的薄板之间相互作用在空间域和波数域都不是局部的^[2]。如果薄板划分得足够薄，则可取薄板中线上的积分近似整个薄板的积分^{[1, 3]}。相对于薄板近似，屏近似对薄板和入射波之间的相互作用值(散射)进行了近似处理^[1]。因此，屏近似在一定的条件下可以理解为薄板近似在弱散射情况下的一种小角度近似。本文重点围绕薄板近似和屏近似法正演实现过程中存在的几个计算问题进行分析讨论。

薄板近似法和屏近似法使用FFT在空间域和波数域之间交替计算，算法模拟一次反射，忽略了非均匀性之间往返传播的交混回响，但可以正确处理与多次前向散射有关的波动现象，如聚焦/焦散、衍射、折射和干涉^[4]。相对于全波场有限差分^[5-6]和有限元法，这种单向传播方法的最大优点是计算速度快，地震波正演模拟过程中可以节省大量内存^[7]。目前该种方法常用于非均匀介质地震散射波场模拟^[8-11]和偏移成像^[12-16]。该种方法对于地震波计算是高效的，特别是对于高频地震波的长距离传播。20世纪90年代，Wu等^[8]利用这种方法模拟了核试验激发的高频弹性Lg波(在地壳中经多次反射形成的波)传播，这是传统的全波有限差分法难以实现的^[7]。

然而，薄板近似和屏近似法在实现过程中存在几个计算问题，具体如下。

(1) F‑K域空间假频问题。这是由于背景Green函数中的1/k_z项的高通滤波效应^[17-19]，会造成很严重的空间假频效应，严重影响地震记录的信噪比。

(2) 背景速度的选取。薄板近似和屏近似法都需要在频率—波数域利用常速度进行相移处理，扰动校正则在空间域进行，如果背景速度与真实速度差异较大时，计算结果将出现很大误差。

(3) 薄板厚度划分的问题。薄板的厚度不仅影响计算精度，而且还影响着计算效率；薄板越厚，计算效率越高，计算精度越低；薄板越薄，计算效率越低，计算精度越高。薄板厚度划分过程中如何满足薄板内速度扰动相对较小是薄板厚度划分的关键问题。

(4) 背景Green函数的计算问题。薄板近似和屏近似计算过程中利用薄板内均匀介质Green函数值近似表示De wolf近似后背景Green函数^[4]，当介质横向非均性很强时，该近似方式的误差相对较大。

(5) 介质的横向非均匀性问题。薄板近似和屏近似法在F-K域利用背景速度完成相移部分，在空间域对速度扰动进行校正，若局部速度扰动变化相对较大、薄板内不满足弱散射条件(不满足Born近似条件)时，该方法计算误差大，这也是该方法的计算瓶颈。

本文的目的是针对薄板近似和屏近似法实现过程中存在的几个计算问题进行分析讨论。首先对薄板近似和屏近似法理论进行回顾；其次围绕F-K域空间假频问题、背景速度的选取、薄板厚度的划分问题、背景Green函数的计算问题、横向非均匀性问题等展开讨论；最后，利用三维简单层状模型和二维实际速度模型验证讨论结果的有效性。

1 薄板近似和屏近似：回顾与分析 1.1 薄板近似理论

二维散射总场可表示为^[11]

$ \begin{array}{l}p(\boldsymbol{r};\omega )={p}_{0}(\boldsymbol{r};\omega )+\\ \;\;\;\;\;\;\;\;{k}_{0}^{2}{\int }_{\boldsymbol{\varOmega }}G(\boldsymbol{r}, {\boldsymbol{r}}^{\text{'}};\omega )o\left({\boldsymbol{r}}^{\text{'}}\right)p({\boldsymbol{r}}^{\text{'}};\omega )\mathrm{d}{\boldsymbol{r}}^{\text{'}}\end{array} $

(1)

式中：$ p(\boldsymbol{r};\omega ) $为总波场；$ {p}_{0}(\boldsymbol{r};\omega ) $为背景波场；$ G(\boldsymbol{r}, {\boldsymbol{r}}^{\text{'}};\omega ) $为背景Green函数；$ \boldsymbol{r}=(x, z) $、$ {\boldsymbol{r}}^{\text{'}}=({x}^{\text{'}}, {z}^{\text{'}}) $，为地下空间点；ω为圆频率；k₀=ω/v₀(z)，为背景波数，其中v₀(z)为深度z处的背景速度；$ o\left(\boldsymbol{r}\boldsymbol{\text{'}}\right)={v}_{0}^{2}\left({z}^{\text{'}}\right)/{v}^{2}\left(\boldsymbol{r}\boldsymbol{\text{'}}\right)-1 $为速度扰动项，其中$ v\left(\boldsymbol{r}\boldsymbol{\text{'}}\right) $为真实速度；Ω为积分区域。

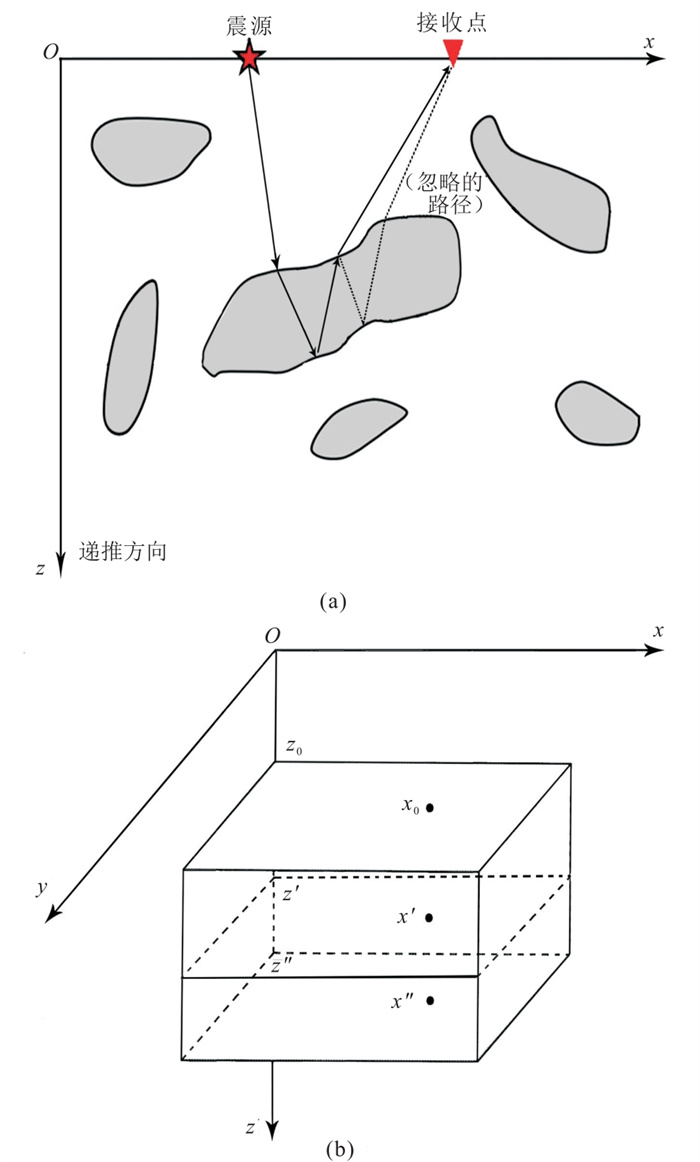
De wolf近似^[4]是一种基于多次前向散射和单次后向散射近似的方法，忽略了内部混响，只保留一次反射波(图 1a)。对模型进行薄板划分(局部薄板如图 1b所示)，$ {z}_{0} $为第一个薄板入射口，$ {z}^{\text{'}} $为第一个薄板出射口，也是第二个薄板的入射口，$ {z}^{″} $为第二个薄板的出射口。假设前向散射场和后向散射场位置分别为$ \left({x}^{\mathrm{*}}, {z}^{\mathrm{*}}\right) $和$ \left({x}^{\mathrm{b}}, {z}^{\mathrm{b}}\right) $，入射波位置位于$ \boldsymbol{r}\boldsymbol{\text{'}}=\left({x}^{\text{'}}, {z}^{\text{'}}\right) $。对于前向散射场(z轴的正方向)，出射波场位于$ \left({x}^{\mathrm{*}}={x}^{″}, {z}^{\mathrm{*}}={z}^{″}\right) $；对于后向散射场(z轴的反方向)，出射波场位于$ \left({x}^{\mathrm{b}}={x}_{0}, {z}^{\mathrm{b}}={z}_{0}\right) $。

首先，将速度模型划分成若干个薄板；其次，对式(1)做傅里叶变换到频率—波数域；然后在每一层薄板内采用局部Born近似；最后，出射的散射波场$ {p}_{\mathrm{s}}\left({k}_{x}^{\mathrm{*}};{z}^{\mathrm{*}};\omega \right) $为^[4]

$ \begin{array}{l}{p}_{\mathrm{s}}\left({k}_{x}^{\mathrm{*}};{z}^{\mathrm{*}};\omega \right)={k}_{0}^{2}{\int }_{{z}^{″}}^{{z}^{\mathrm{*}}}\mathrm{d}z\times \\ \int \mathrm{d}x{G}_{0}\left({k}_{x}^{\mathrm{*}};{z}_{j}^{\mathrm{*}};\boldsymbol{r}\boldsymbol{\text{'}};\omega \right) \mathrm{F}\mathrm{T}\left[o\left(\boldsymbol{r}\boldsymbol{\text{'}}\right){p}_{0}(\boldsymbol{r}\boldsymbol{\text{'}};\omega )\right]\end{array} $

(2)

式中：FT表示傅里叶变换；$ {k}_{x}^{\mathrm{*}} $为横向波数；$ {G}_{0}({k}_{x}^{\mathrm{*}};{z}_{j}^{\mathrm{*}};\boldsymbol{r}\boldsymbol{\text{'}};\omega ) $的表达式为

$ {G}_{0}\left({k}_{x}^{\mathrm{*}};{z}_{j}^{\mathrm{*}};\boldsymbol{r}\boldsymbol{\text{'}};\omega \right)=\frac{\mathrm{i}}{2{k}_{{z}_{j}}}{\mathrm{e}}^{\mathrm{i}{k}_{{z}_{j}}\left({z}^{\mathrm{*}}-z\mathrm{\text{'}}\right)}{\mathrm{e}}^{-\mathrm{i}{k}_{x}^{\mathrm{*}}x\mathrm{\text{'}}} $

(3)

式中：$ {k}_{{z}_{j}}=\sqrt{{k}_{0}^{2}\left(j\right)-{\left({k}_{x}^{\mathrm{*}}\right)}^{2}} $为第j个薄板内的垂直波数，$ {k}_{0}\left(j\right) $为第j个薄板内的背景波数。式(2)可简化为^[4]

$ \begin{array}{l}{p}_{\mathrm{s}}\left({k}_{x}^{\mathrm{*}};{z}^{\mathrm{*}};\omega \right)=\frac{\mathrm{i}{k}_{0}^{2}}{4\mathrm{\pi }{k}_{z}}{\mathrm{e}}^{\mathrm{i}{k}_{{z}_{j}}\mathrm{\Delta }z}\int \mathrm{d}{k}_{x}^{\text{'}}{\int }_{{z}^{″}}^{{z}^{\mathrm{*}}}\mathrm{d}z\times \\ \int \text{d}xo(x, z){p}_{0}\left({k}_{x}^{\text{'}};{z}^{\text{'}};\omega \right){\mathrm{e}}^{-\mathrm{i}\left({k}_{z}^{\mathrm{*}}-{k}_{z}^{\text{'}}\right)z}{\mathrm{e}}^{-\mathrm{i}\left({k}_{x}^{\mathrm{*}}-{k}_{x}^{\text{'}}\right)x}\end{array} $

(4)

式中：$ {k}_{x}^{\text{'}} $为深度$ {z}^{\text{'}} $处水平波数，$ {k}_{z}^{\text{'}} $、$ {k}_{z}^{\mathrm{*}} $分别为深度$ {z}^{\text{'}} $和深度$ {z}^{\mathrm{*}} $处的垂直波数；$ \mathrm{\Delta }z={z}^{\mathrm{*}}-{z}^{\text{'}} $。式(4)称为标量双域薄板公式。

1.2 屏近似理论

为了提高计算效率，将薄板压缩成屏，这样把二维薄板压缩成一维屏，对薄板和入射波之间相互作用值(散射)进行近似处理，即可取薄板中线上的积分近似整个薄板的积分。对式(4)进一步化简可以得到前向散射场$ {p}_{\mathrm{s}}^{\mathrm{*}}\left({k}_{x};{z}^{″};\omega \right) $和后向散射场$ {p}_{\mathrm{s}}^{\mathrm{b}}\left({k}_{x};{z}_{0};\omega \right) $分别为

$ \begin{array}{l}{p}_{\mathrm{s}}^{\mathrm{*}}\left({k}_{x};{z}^{″};\omega \right)={k}_{z}{\mathrm{e}}^{\mathrm{i}{k}_{z}\mathrm{\Delta }z}\times \\                \mathrm{F}\mathrm{T}\left[\mathrm{i}\omega F({x}^{\text{'}}, {z}^{\text{'}})\mathrm{\Delta }zp\left(x, {z}^{\text{'}};\omega \right)\right]\end{array} $

(5)

$ \begin{array}{l}{p}_{\mathrm{s}}^{\mathrm{b}}\left({k}_{x};{z}_{0};\omega \right)=\frac{{k}_{0}}{{k}_{z}}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\left(\mathrm{\Delta }z\right){\mathrm{e}}^{\mathrm{i}{k}_{0}\mathrm{\Delta }z}{\mathrm{e}}^{\mathrm{i}{k}_{z}\mathrm{\Delta }z}\times \\            \mathrm{F}\mathrm{T}\left[\mathrm{i}\omega F({x}^{\text{'}}, {z}^{\text{'}})\mathrm{\Delta }zp({x}^{\text{'}}, {z}^{\text{'}};\omega )\right]\end{array} $

(6)

式中

$ F(x, {z}^{\text{'}})=\frac{1}{2{v}_{0}\left({z}^{\text{'}}\right)}\left[\frac{{v}_{0}^{2}\left({z}^{\text{'}}\right)}{{v}^{2}({x}^{\text{'}}, {z}^{\text{'}})}-1\right] $

(7)

$ \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\left(\mathrm{\Delta }z\right)=\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{\Delta }z\right)/\mathrm{\Delta }z $

(8)

由式(6)和式(7)可以看出前向散射或透射波$ {p}_{\mathrm{s}}^{\mathrm{*}}({x}^{″}, {z}^{″};\omega ) $主要由速度扰动控制；而反向散射或反射波$ {p}_{\mathrm{s}}^{\mathrm{b}}\left(x, {z}_{0};\omega \right) $由阻抗扰动控制。因此，总的前向散射场$ {p}^{\mathrm{*}}({x}^{″}, {z}^{″};\omega ) $和后向散射场$ {p}^{\mathrm{b}}\left(x, {z}_{0};\omega \right) $可以表示为

$ \begin{array}{l}{p}^{\mathrm{*}}({x}^{″}, {z}^{″};\omega )={p}_{0}({x}^{″}, {z}^{″};\omega )+{p}_{\mathrm{s}}^{\mathrm{*}}({x}^{″}, {z}^{″};\omega )\\ =\mathrm{F}{\mathrm{T}}^{-1}\left\{{\mathrm{e}}^{\mathrm{i}{k}_{z}\mathrm{\Delta }z}\mathrm{F}\mathrm{T}\left[p\right({x}^{\text{'}}, {z}^{\text{'}};\omega \left)\right]\right\}+\\ \mathrm{F}{\mathrm{T}}^{-1}\left\{\frac{{k}_{0}}{{k}_{z}}{\mathrm{e}}^{\mathrm{i}{k}_{z}\mathrm{\Delta }z}\mathrm{F}\mathrm{T}\left[\mathrm{i}\omega F({x}^{\text{'}}, {z}^{\text{'}})\mathrm{\Delta }zp\left({x}^{\text{'}}, {z}^{\text{'}};\omega \right)\right]\right\}\end{array} $

(9)

$ \begin{array}{l}{p}^{\mathrm{b}}\left(x, {z}_{0};\omega \right)={p}_{0}(x, {z}_{0};\omega )+{p}_{\mathrm{s}}^{\mathrm{b}}(x, {z}_{0};\omega ) \\ =\mathrm{F}{\mathrm{T}}^{-1}\left\{{\mathrm{e}}^{\mathrm{i}{k}_{z}\mathrm{\Delta }z}\mathrm{F}\mathrm{T}\left[p\left(x, {z}^{\text{'}};\omega \right)\right]\right\}+\\ \mathrm{F}{\mathrm{T}}^{-1}\left\{\frac{{k}_{0}}{{k}_{z}}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\left(\mathrm{\Delta }z\right){\mathrm{e}}^{\mathrm{i}{k}_{0}\mathrm{\Delta }z}{\mathrm{e}}^{\mathrm{i}{k}_{z}\mathrm{\Delta }z}\times \right.\\ \left.\mathrm{F}\mathrm{T}\left[\mathrm{i}\omega F({x}^{\text{'}}, {z}^{\text{'}})\mathrm{\Delta }zp\left(x, {z}^{\text{'}};\omega \right)\right]\right\}\end{array} $

(10)

式中FT^-1表示傅里叶反变换。式(9)和式(10)即为广义屏前向和后向延拓算子，对于反向传播的波场，i前面取负号即可。

为了提高算子的稳定性，需对$ {k}_{0}/{k}_{z} $项做近似处理，目前公开的方法有如下几种。

(1) 对$ {k}_{0}/{k}_{z}=\sqrt{1-{v}_{0}^{2}{k}_{x}^{2}/{\omega }^{2}} $做Taylor展开，有

$ \frac{{k}_{0}}{{k}_{z}}\approx 1+\frac{1}{2}\frac{{v}_{0}^{2}{k}_{x}^{2}}{{\omega }^{2}}-\frac{1}{8}{\left(\frac{{v}_{0}^{2}{k}_{x}^{2}}{{\omega }^{2}}\right)}^{2}+\frac{1}{16}{\left(\frac{{v}_{0}^{2}{k}_{x}^{2}}{{\omega }^{2}}\right)}^{3} $

(11)

该处理能有效地保证算法的稳定性，但是计算精度与展开阶次有关，阶数越高，计算精度越高。

(2) 当地震波小角度传播时，可以令k₀/k_z≈1，进行简化计算，以保证计算的稳定性。

(3) 对$ {k}_{0}/{k}_{z} $用连分式展开，并令$ {B}^{2}={k}_{x}^{2}/{k}_{0}^{2} $，则可近似表示为

$ {k}_{0}/{k}_{z}\approx 1+0.5{B}^{2}/(1-0.75{B}^{2}) $

(12)

上式只有在$ {k}_{x}^{2}/{k}_{0}^{2} $=4/3的极端情况才会出现奇异，稳定性大大提高。

(4) 高角度近似。对k₀/k_z项利用Taylor展开，可得

$ \begin{array}{l}\frac{{k}_{0}}{{k}_{z}}\approx 1+0.5{\left(\frac{{k}_{x}}{{k}_{0}}\right)}^{2}+0.375{\left(\frac{{k}_{x}}{{k}_{0}}\right)}^{4}+\\ 0.3125{\left(\frac{{k}_{x}}{{k}_{0}}\right)}^{6}+0.2734375{\left(\frac{{k}_{x}}{{k}_{0}}\right)}^{8}\end{array} $

(13)

但是当横向变化强烈或频率高时，上式会出现不稳定现象，一般需要满足稳定性条件^[16]

$ \left|\omega \mathrm{m}\mathrm{a}\mathrm{x}\left[F(x, z)\right]\mathrm{\Delta }z\right| < \beta $

(14)

式中β一般取0.10~0.15。

2 计算问题的讨论分析

薄板近似和屏近似法计算过程中利用快速傅里叶变换(FFT)在空间域和波数域之间交替进行，一般包括两项：自由传播、相位屏。自由传播是在波数域通过一个均匀的参考速度进行计算，参考速度可以随深度变化；相位屏项体现波和介质非均匀部分的相互作用，是在空间域计算。该方法的优点是不会产生离散化的网格频散现象且对网格间距的要求低，计算效率高。然而计算过程中存在几个计算问题，本文重点围绕F-K域空间假频问题、背景速度选取、薄板厚度的划分、横向不均匀介质中的Green函数计算、介质的横向不均匀性处理等问题展开。

2.1 F-K域空间假频问题

式(9)和式(10)中的k_z项二维情况下可以表示为$ \sqrt{{\omega }^{2}/{v}_{0}^{2}-{k}_{x}^{2}} $，同时也可以等效为^[17]

$ {k}_{z}=\frac{\omega }{{v}_{0}}\sqrt{1-\frac{{v}_{0}^{2}{k}_{x}^{2}}{{\omega }^{2}}}=\frac{\omega }{{v}_{0}}\mathrm{c}\mathrm{o}\mathrm{s}\theta $

(15)

式中θ为地震波传播角度。$ 1/{k}_{z} $项关系到横向能量的衰减^[24]。令S=$ 1/{k}_{z}={v}_{0}/\left(\omega \mathrm{c}\mathrm{o}\mathrm{s}\theta \right) $。当$ \theta \in \left[{0}^{o}, {90}^{o}\right] $时，cosθ单调递减，因此，S项单调递增。当θ趋于90°时，S项趋于无穷大，对应的波场值也会出现无穷大，导致两侧的散射波能量衰减太慢，形成空间假频。这种现象可以理解为算子的高通滤波响应(传播角度接近90°)^[17-19]。

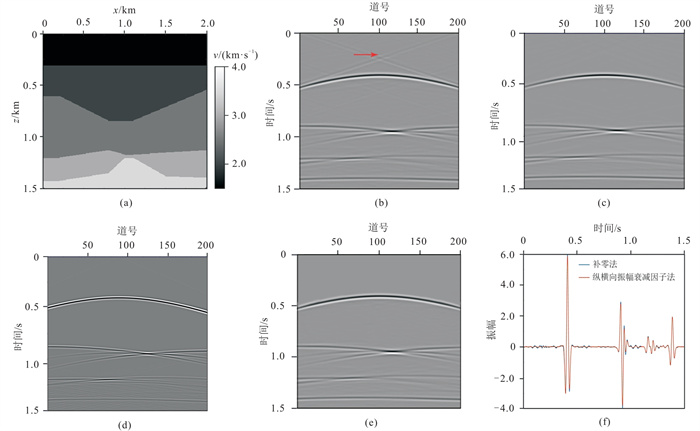
正演结果中(速度模型参数如图 2a所示)会出现很严重的空间假频效应(图 2b红色箭头所示)，虽然计算过程中一般会对S项进行近似处理(保证算法的稳定性)，但是没有改变延拓算子的高通滤波特性。

目前解决上述空间假频问题的公开方法主要有两种：一种是在x、z和t方向补一倍以上的零值，该方法虽然可以有效地消除这种空间假频，但是计算量也随之增加；另一种是通过改变S的高通滤波特性^[18-20]，令

$ {S}^{\text{'}}={k}_{z}/\sqrt{{a}^{2}{k}_{x}^{2}+{k}_{z}^{2}} $

(16)

式中a为常数。S化简为

$ \begin{array}{l}S=\frac{1}{{k}_{z}}\cdot S\mathrm{\text{'}}=\frac{1}{\sqrt{{\omega }^{2}/{v}_{0}^{2}-({a}^{2}-1){k}_{x}^{2}}}\\ =\frac{{v}_{0}}{\omega \sqrt{{a}^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\theta }}\end{array} $

(17)

当a=1时，便能够消除空间假频现象；a > 1时，S随倾角的增大而减小，能进一步衰减散射波两翼的能量；a < 1时，S随倾角的增大而增大，使空间假频现象更严重。

上述算子虽然可以对横向能量进行衰减，但是也会导致浅部衰减量比深部的衰减量大。因此，需要对修正因子做进一步处理，引入与深度有关的修正因子^[18]，具体为

$ l\left(j\right)=1-\left[1-{s}_{z}\right]\mathrm{s}\mathrm{i}\mathrm{n}\frac{\mathrm{\pi }j}{2(N-1)} $

(18)

式中：$ l\left(j\right) $为深度为$ z $_j处的修正因子；N为深度网格总数；$ j=\mathrm{0, 1}, \cdots , N-1 $；$ {s}_{z} $为深度为$ z $处的衰减系数，假设顶层为1，底层为一个很小的数字(0.01)。在计算S的过程中乘上$ {l}_{z}\left({z}_{j}\right) $就可以解决空间假频问题。

利用纵、横向振幅衰减因子改变算子（1/k_z项）的高通滤波特性后，正演地震记录(图 2c)中的空间假频消失。为了进一步分析该方法的正确性，分别与传统的补零法(图 2d)和有限差分法(图 2e)进行对比，补零法同样可以消除空间假频现象，而有限差分法则不存在这一问题，三者的计算时间分别为39、204、83 s，可见，传统补零消除法计算量最大，纵横向振幅衰减因子法与未处理前计算量(38 s)几乎相当，且计算效率高于传统有限差分法。横向振幅衰减因子消除了浅部的空间假频现象的同时，一定程度上也降低了浅部反射波两边的振幅，该方法对深部反射信号影响很小。

图 2c中的地震记录两边振幅弱，其原因是纵横向振幅衰减因子法对于空间假频重合的地震记录也进行了衰减，但是对深部后向散射振幅影响很小。该方法是计算一次反射波，因此地震记录中没有多次波信号，而有限差分法则可以模拟出多次波信号(图 2e)。分别抽取图 2c和图 2d中地震记录的中间一道进行对比，结果如图 2f所示。由图可知，两种去假频方法的结果基本一致，验证了纵横向振幅衰减因子法的有效性。

2.2 背景速度选取问题

在每个薄板内(屏内)将速度表示成为背景速度和扰动速度的叠加，而自由传播是在波数域通过选取一个均匀背景速度参数(常数)进行的，如何选择背景参数对最终的计算结果非常重要。一般情况下有以下几种选法。

(1) 薄板内最小速度v_min。如果介质中存在几个高速体，整体速度偏低时，正演过程中背景速度选择v_min；

(2) 薄板内最大速度v_max。如果介质中存在某几个低速体，整体速度偏高时，正演过程中背景速度选择v_max；

(3) 薄板内平均速度$ \stackrel{-}{v} $。如果薄板内整体速度变化比较剧烈时，速度差异较大，此时应该选择平均速度$ \stackrel{-}{v} $作为相移的背景速度。

综上所述，背景速度的选择上要尽可能地保证薄板内整体速度扰动相对较小，根据不同的情况选择相应的背景速度，为后续空间域校正提供一个相对准确的参数。

2.3 薄板厚度划分问题

薄层或者薄板是一个相对概念，传统意义上的薄层是指小于1/4子波波长或者调谐厚度(垂直分辨率)，一般子波的波长约为80~100 m，调谐厚度则为20~25 m，大于一个子波波长的则为厚层。因此，网格厚度小于20~25 m为薄板，大于80~100 m为厚板。本文主要考虑薄板，即厚度小于20~25 m。

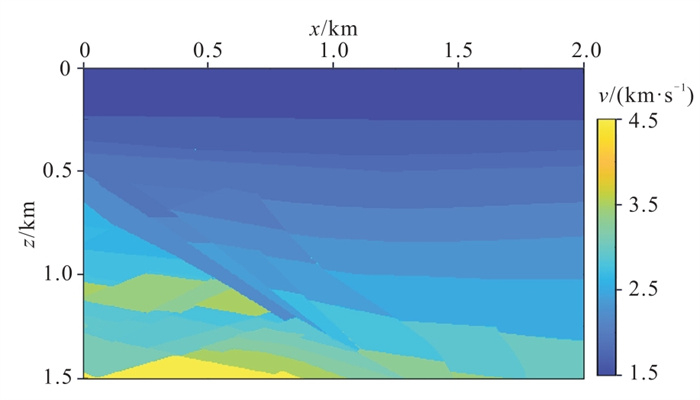
将整个模型沿着深度方向上划分成一个个薄板后，采用De wolf近似对总波场不断更新，并在每一步内计算一次向后散射波场。薄板厚度的划分不仅影响计算精度，而且还影响着计算效率。用图 3的速度模型进行试算。模型在x、z方向上的网格点数分别为401和301，网格间距为5 m；观测系统参数为：采用中间放炮方式，震源位于(1000 m，5 m)处，道间距为5 m，每炮200道；采样间隔为1 ms，样点数为1600；震源函数是主频为30 Hz的Ricker子波。

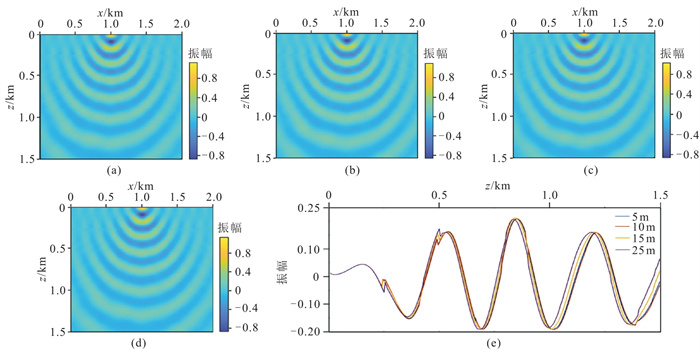
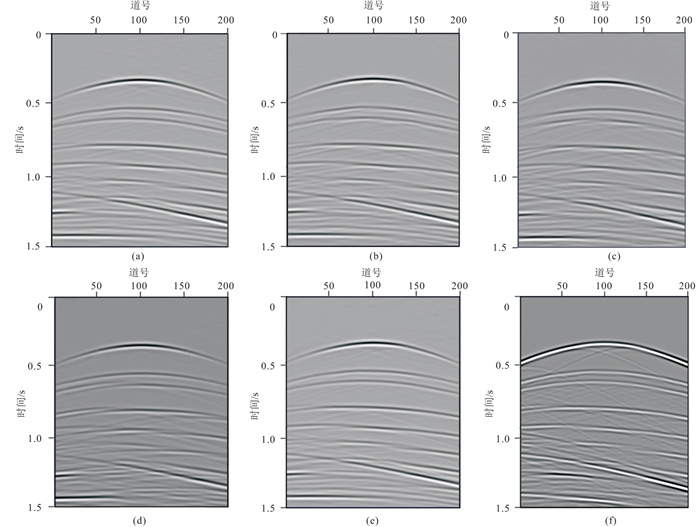
分别设置薄板厚度为5、10、15、25 m，薄板近似法计算的20 Hz单频的波场如图 4a~图 4d所示。由图可知：薄板厚度为5、10 m单频波场的相位和振幅信息基本一致，当薄板厚度为15、25 m时，单频波场的相位和振幅出现差异(图 4e)，原因是随着薄板厚度的加大，对模型简化程度已经与真实模型出现差距，薄板内的等效速度参数与真实模型速度参数差异较大。为了进一步验证上述结果，开展薄板近似正演研究，不同厚度的薄板近似的正演地震记录如图 5a~图 5d所示。图 5e为屏近似法正演地震记录(在薄板厚度为5 m基础上进行屏近似)。图 5f为传统有限差分法的正演地震记录，相对于薄板近似和屏近似法，有限差分法波场信息更丰富，其原因是有限差分能够模拟出多次波信号，薄板近似和屏近似计算过程中忽略薄板内的多次波信号。有限差分法浅部反射信号两边的波形振幅强，薄板近似和屏近似法两边振幅相对较弱，原因有两个：一个是薄板近似和屏近似在高角度下计算误差相对大，正演过程中限制传播角度来保证精度，导致两边高角度信号振幅弱；另一个是纵、横向振幅衰减因子消除了浅部的空间假频现象的同时，一定程度上也降低了浅部反射波的两边的振幅。

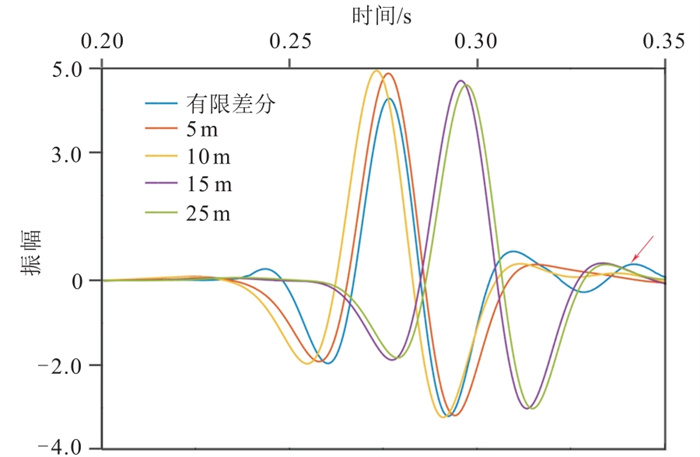
为进一步分析不同薄板厚度对计算结果的影响，抽取x=1.0 km处单道，并与有限差分法结果进行对比(图 6)。由图 6可知：屏近似与薄板厚度为5、10 m的薄板近似计算结果整体类似，与有限差分结果相当，但有限差分法可以模拟出多次波信号(红色箭头所示)，薄板近似和屏近似计算过程中忽略薄板内的多次波信号。当薄板厚度为15、25 m时，地震记录差异较大，地震波相位出现明显差别，其原因是随着薄板厚度的加大，对模型简化过程中已经与真实模型出现差距，薄板内的等效速度不能有效满足实际情况。在相同的计算环境下，屏近似和厚度为5、10、15、25 m的薄板近似的单炮计算时间分别为42、59、32、22、16 s，随着厚度的增加，薄板近似正演所需的时间逐渐减少。当薄板厚度相同的情况下，屏近似法的计算效率高于薄板近似。

如何对薄板厚度进行划分是一个值得讨论的问题，一般情况沿着深度方向进行薄板划分，这种划分形式不能改变同一深度的横向非均匀性扰动，但是可以改变不同深度的非均匀性扰动带来的影响。薄板近似划分的重点是要保证薄板内的扰动相对较小，以满足Born近似条件，同时减少利用局部均匀背景Green函数代替De wolf近似后背景Green函数的误差^[4]。因此，当介质沿着深度方向的速度扰动相对较弱(非均匀性相对较弱时)时，薄板可以相对厚一些；当介质扰动相对较强时，薄板可以薄一些；薄板划分的越多(厚度小)，计算效率越低，计算精度相对较高；薄板划分的越少(厚度大)，计算效率越高，但是计算精度相对较低。当薄板压缩成“屏”，薄板中的非均匀体产生的波场相当于由薄板中央处(此时的薄板厚度为一个延拓步长)的一个“屏”产生，此时，薄板退化为“屏”，该过程对薄板和入射波之间相互作用值(散射)进行了近似处理，因此，提高了计算效率。

2.4 横向非均匀介质中的背景Green函数计算问题

当$ {k}_{0}^{2}\le {k}_{x}^{2} $时，背景Green函数(式(3))就会出现不稳定现象，这是Green函数的数学形式决定的，尽量避免高频信号的计算。常规的处理办法就是让这部分不稳定信号全部取零值，或者对传播角度进行限制，从而保证算子的稳定性。由于$ 1/{k}_{z} $存在不稳定性，一般对该项进行近似处理(式(11)~式(13))。

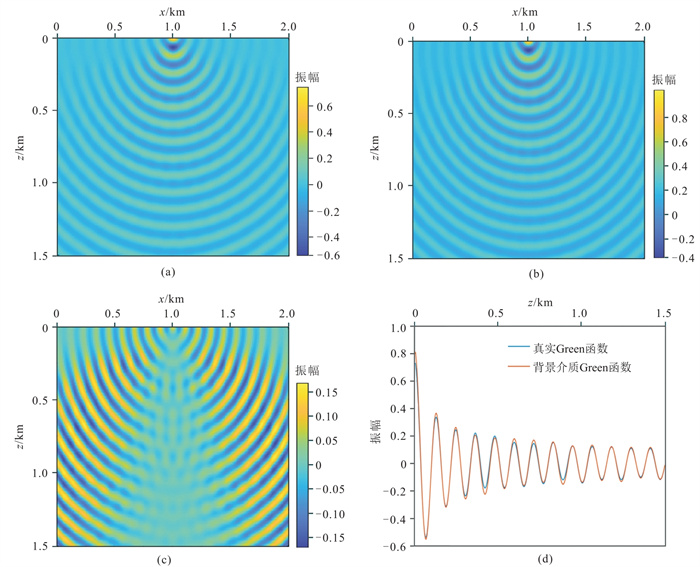
薄板近似和屏近似计算过程中，为了加快计算效率，通常在局部计算过程中，利用薄板内均匀介质Green函数近似表示De wolf近似后背景Green函数。为了定量分析这种近似产生的误差，真实均匀速度参数设置为2000 m/s，背景速度参数设置为1800 m/s。图 7a、图 7b分别为真实Green函数和背景速度参数的Green函数，两者的误差如图 7c所示，由图可知：当传播角度较小时，误差相对较小；随着传播角度的变大，误差随之变大。抽取x=1.0 km处两种Green函数进行单道对比(图 7d)。因此，当横向非均匀性较强时，该近似处理的误差相对较大。薄板近似和屏近似是在双域交替计算，在波数域计算时，不能处理介质的横向非均匀性，只能利用背景速度值进行计算，这种近似在薄板内扰动较小的时候，误差满足精度要求，但是当速度扰动较大时，误差也随之增加。因此，薄板划分过程中尽可能的薄，可以有效地减小该近似处理的误差。

2.5 介质的横向非均匀性问题

当薄板划分很薄时，薄板内只存在横向不均匀性，沿着深度方向则认为是均匀的。薄板近似和屏近似法在F-K域利用背景速度完成相移部分，在空间域对速度扰动进行校正。为分析算子适应介质速度横向变化的能力，将真实速度设置为3.0 km/s，背景参数分别设置为2.7、2.4、1.8、1.5 km/s，不同速度扰动的脉冲响应结果如图 8所示。由图可知：随着速度扰动程度的增加，脉冲曲线逐渐偏离理想曲线，当扰动为速度值的一半时，相对误差最大。

当局部存在强扰动时，会导致算子的补偿精度不足，其原因是这几种近似导致的，具体如下。

(1) 局部的Born近似。当薄板内扰动较小时，利用常规延拓算子能够正常处理，但是当横向变化强烈或频率高(不满足Born近似条件)，空间域的校正项就不能正确对误差进行补偿。

(2) De Wolf近似后的背景介质Green函数利用均匀介质背景Green函数值近似。为了简化计算，薄板近似和屏近似在计算扰动过程中均利用局部均匀介质Green函数值近似De wolf近似后背景Green函数，该近似的条件要求是薄板内扰动较小。

因此，尽可能地保证薄板内扰动较小是保证两种算子精度的基本条件，薄板划分过程中要尽可能的薄。但是该处理方式并不能适应横向存在局部强扰动，这也是该方法的计算瓶颈问题。如何进一步提高算子适应速度横向变化的能力，即提高Born近似适应局部强散射介质的能力，本文给出了几种解决方案及其初步试算结果。

(1) 采用高阶的Born级数。当介质存在强散射时，散射序列中高阶项产生的影响不可忽略，这时采用一阶Born近似就会有较大的误差。因此，为了提高计算精度，需要采用高阶Born近似，但会导致计算量大大增加、收敛慢。

(2) 在薄板近似和屏近似计算结果的基础上，在薄板内进行空间域有限差分补偿，即FFD法^[20]，从而提高算子的计算精度。

(3) T矩阵方法。Jakobsen等^[21]利用De Wolf级数和T矩阵重新推导了De Wolf散射级数，并对其收敛特征进行了详细的分析。

(4) 广义Born级数。Kleinman等^[22]将解泛函方程的超松弛理论用于解决光学中的强散射问题，徐杨杨等^[23]分析和讨论了该方法在反射地震条件下的算法表现、收敛特点、计算效率以及计算精度等问题。研究结果表明该方法可以有效地克服Born级数的弱点。将超松弛迭代法与Lippmann-Schwingr(L-S)方程相结合，构成广义的Born级数，则广义Born级数的迭代形式为^[23]

$ \begin{array}{l}{p}_{n}(\boldsymbol{r};\omega )={\alpha }_{n}{p}_{0}(\boldsymbol{r};\omega )+\\                 \left[I\left(\boldsymbol{r}\right)-{\alpha }_{n}L(\boldsymbol{r};\omega )\right]{p}_{n-1}(\boldsymbol{r};\omega )\end{array} $

(19)

式中：$ {p}_{n}(\boldsymbol{r};\omega ) $为第n次迭代的总前向场；$ L(\boldsymbol{r};\omega )=I\left(\boldsymbol{r}\right)-A(\boldsymbol{r};\omega ) $，$ I\left(\boldsymbol{r}\right) $的每个位置参数为1，$ A(\boldsymbol{r};\omega )={k}_{0}^{2}{\int }_\boldsymbol{\varOmega }G(\boldsymbol{r}, \boldsymbol{r}\text{'})o\left(\boldsymbol{r}\right)\mathrm{d}\boldsymbol{r} $；$ {\alpha }_{n} $为松弛因子

$ {\alpha }_{n}=\frac{{\int }_{\boldsymbol{\varOmega }}{p}_{n-1}(\boldsymbol{r};\omega )B(\boldsymbol{r};\omega )\mathrm{d}\boldsymbol{r}}{{\int }_{\boldsymbol{\varOmega }}B(\boldsymbol{r};\omega )\overline{B(\boldsymbol{r};\omega )}\mathrm{d}\boldsymbol{r}} $

(20)

其中：$ B(\boldsymbol{r};\omega )=L(\boldsymbol{r};\omega ){p}_{n-1}(\boldsymbol{r};\omega ) $；$ \overline{B(\boldsymbol{r};\omega )} $是$ B(\boldsymbol{r};\omega ) $的共轭。每次迭代后，更新松弛因子$ {\alpha }_{n} $。

网格尺寸为301×151，空间网格间距为10 m，真实速度为3000 m/s，背景速度设置为2600 m/s。将超松弛迭代与De Wolf近似结合，形成局部的广义Born级数，即在薄板内进行超松弛迭代，利用更为精确的数值解代替局部的Born近似。一阶超松弛迭代后的脉冲响应结果如图 9所示，由图可知：相对于薄板近似算子和屏近似算子，经过一阶超松弛迭代后的算子适应横向变化的能力增强。

(5) 基于背景介质吸收化加预处理的级数。首先在背景波数中引入一个小的虚部分量，与Lippmann-Schwingr(L-S)方程对应的背景格林函数带有一个阻尼因子。然后，利用一个借助于上述小虚部分量定义的预解因子对带有复波数的L-S方程进行预处理。最后，利用迭代法对经过预处理的L-S方程进行迭代求解，得到经过复波数和预处理改进的Born级数，经过这样改进的Born级数对于强散射也是绝对收敛的^[24]。具体表达式为

$ \begin{array}{l}{p}_{n}(\boldsymbol{r};\omega )=\gamma {p}_{0}(\boldsymbol{r};\omega ) +\\                   \gamma {p}_{0}(\boldsymbol{r};\omega )\sum\limits_{n=1}^{\infty }{\widetilde{M}}^{n}(\boldsymbol{r};\omega )\end{array} $

(21)

式中：$ \gamma =\mathrm{i}{\omega }^{2}\tilde{o}(\boldsymbol{r};\omega )/ε $，为预解因子，其中$ ε \ge \mathrm{m}\mathrm{a}\mathrm{x}\left|{\omega }^{2}\tilde{o}\right(\boldsymbol{r};\omega \left)\right| $，$ \tilde{o}(\boldsymbol{r};\omega )=o\left(\boldsymbol{r}\right)-\mathrm{i}ε /{\omega }^{2} $；$ \widetilde{M}(\boldsymbol{r};\omega )=\gamma A(\boldsymbol{r};\omega )-\gamma +1 $。

为了测试方法的有效性，将背景速度设置为3400 m/s，真实速度为3000 m/s。脉冲响应结果如图 10所示，可见，经过处理后的延拓算子适应横向变化的能力变强。

3 三维和二维模型试算 3.1 三维层状模型试算

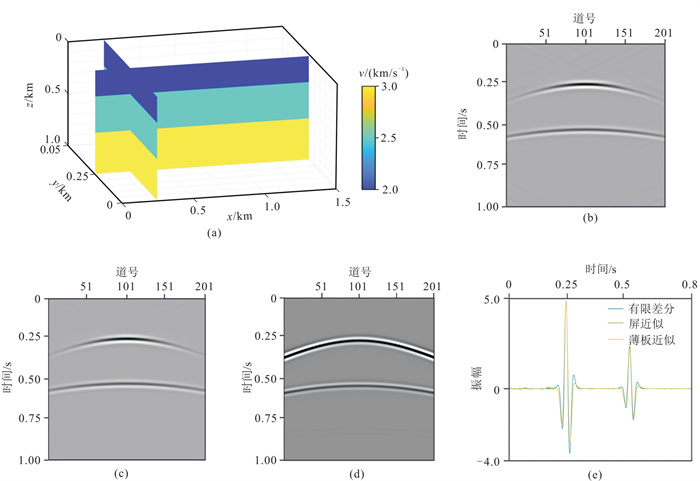
为了验证薄板近似和屏近似法的计算效率，利用三维层状介质速度模型进行测试(图 11a)。模型网格数为301×201×101，网格尺寸为5 m。震源位于(750 m，250 m，5 m)，采用中间放炮的观测系统，道间距为5 m，首个检波器位于(250 m，250 m，5 m)，最后一个检波器为(1250 m，250 m，5 m)，共201道。震源子波主频为20 Hz，采样长度为1000个，采样间隔为1 ms。

由于介质横向是均匀的，没有速度扰动，因此，测试主要目的有两个，一个是纵横向振幅衰减因子法是否可以消除三维空间假频；另一个是对薄板划分厚度对计算精度和计算效率的影响。因此，薄板厚度设置为10 m，有限差分的网格尺寸为5 m。薄板近似和屏近似正演结果分别如图 11b、图 11c所示，有限差分法正演结果如图 11d所示。薄板近似和屏近似计算结果波形和振幅相似，有限差分法浅部反射信号两边的波形振幅强，薄板近似和屏近似法两边振幅相对较弱。图 11e为模拟地震记录第100道的波形对比，三种方法的波形和振幅基本一致。

薄板厚度为5 m时，薄板近似和屏近似法所需的时间为613 s、516 s，当薄板厚度为10 m时，所需时间为523 s、412 s，而有限差分法的计算时间为1129 s。结合波形对比结果可知：纵横向振幅衰减因子法能够有效地消除三维空间假频问题，且薄板厚度为10 m的正演结果与振幅归一化后的有限差分法的正演结果波形基本一致，但是计算时间大大减小。可见，薄板近似和屏近似的计算效率高于有限差分法。

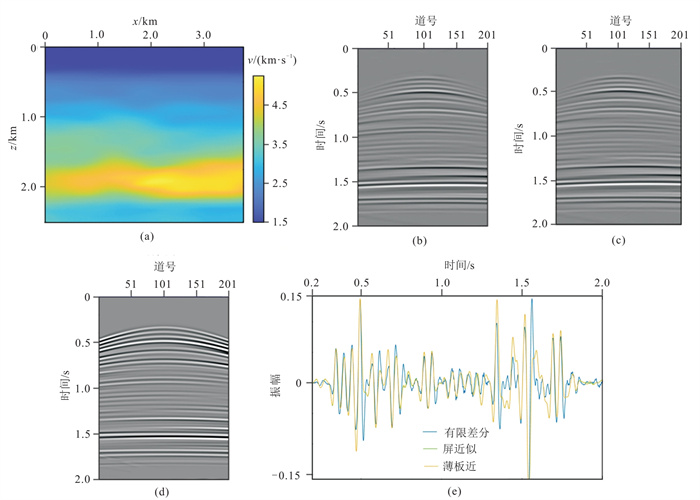
3.2 二维实际速度模型试算

利用实际速度模型进行计算，实际速度模型如图 12a所示。模型网格数为751×501，网格间距为5 m；震源位于(2500 m，5 m)，200个检波器接收，道间距为5 m。时间样点数为1000，采样间隔为2 ms。利用实际速度模型开展薄板近似和屏近似研究，根据讨论内容，正演过程中相关参数设置如下：①薄板的厚度设置为一个延拓步长，即5 m(保证薄板内的弱散射性)；②背景速度设置为一个薄板内的平均速度；③利用纵横向振幅衰减因子法消除空间假频问题；④利用薄板内均匀介质Green函数近似表示De wolf近似后背景Green函数。三种方法模拟结果分别如图 12b~图 12d所示，第100道的波形对比如图 12e所示。由图 12可见：屏近似法和薄板近似法的数值模拟地震记录的波形相位和振幅相似。与有限差分法结果相比，深部反射波信息相似，有限差分法的地震记录浅部两边反射波双曲线振幅强于薄板近似和屏近似法。其原因有两个，一个是为了减少误差，限制了地震波传播角度，导致高角度地震波振幅弱(双曲线两边)；另一个是纵、横向振幅衰减因子消除了浅部的空间假频现象的同时，也降低了浅部反射波的两边的振幅，该因子对深部反射波影响相对较小。光滑后的速度模型能够有效消除内反射，有限差分法的多次波信号变弱，因此，振幅归一化后的有限差分法正演地震记录与薄板近似和屏近似计算的一次反射波地震记录整体相似。进一步验证上述讨论结果的有效性。屏近似法、薄板近似和有限差分法正演模拟的计算时间分别为189、218和289 s，说明屏近似法、薄板近似法计算效率高于传统的有限差分法。

4 结论与展望

为实现De Wolf近似，Wu在20世纪90年代提出了薄板近似和屏近似，并给出了相应的实现算法。本文详细讨论了算法实现过程中存在几个计算问题和解决方案。首先，讨论分析了两种算子对地层倾角的高通滤波响应造成空间假频效应的原因，并利用纵、横向振幅衰减因子消除了空间假频现象；其次，对背景速度的选取进行了探究，尽可能的保证薄板内整体速度扰动相对较小是背景速度选择的关键；然后，对比了不同薄板厚度下薄板近似和屏近似法的正演记录及其计算效率，并探讨了薄板划分的依据；随后，利用薄板内均匀介质Green函数近似表示背景介质Green函数是造成算子在非均匀介质中存在计算误差的原因之一，薄板划分过程中尽可能的薄，保证在整个薄板内是弱扰动，从而减小该近似处理的误差；最后研究了介质横向不均匀性对薄板近似和屏近似精度的影响及其原因，针对这一计算瓶颈问题，讨论了几种解决办法，以提高算子适应速度横向变化的能力。简单的三维模型及实际二维速度模型试算进一步验证了本文讨论结果的有效性。

本文讨论结果有助于提高复杂介质下的薄板近似和屏近似法的计算精度。