2. 海洋油气勘探国家工程研究中心, 北京 100028;
3. 吉林大学仪器科学与电气工程学院, 吉林长春 130061
2. National Engineering Research Center of Offshore Oil and Gas Exploration, Beijing 100028, China;
3. College of Instrumentation and Electrical Engineering, Jilin University, Changchun, Jilin 130061, China
地震波场数值模拟在地震勘探多个技术环节中扮演着重要角色,采用不同数值算法离散求解各种地震波动方程是地震数值模拟的核心。在众多数值算法中,有限差分法因其简单易行、计算高效和灵活性高等优点而广受青睐[1-5]。但是,采用有限差分算子近似离散波动方程中的时间和空间偏导数时,通常会在时间域或空间域产生较强的数值频散。因此,提高有限差分在波场延拓中的精度、效率和灵活性一直是重要的研究内容[6-9]。
现有差分方法可以通过增加差分算子长度提高空间域模拟精度。在传统规则网格高阶差分基础上,学者们发展了多种改进有限差分法,如交错网格与旋转交错网格差分方法[2, 8-11]、隐式差分方法[12-16]、优化差分方法[17-19]、基于时间—空间域频散关系求取差分系数的高阶差分方法[20-21]、波场外推在频率—空间域实现的差分方法[22-23]等。然而这些改进方法主要聚焦于提高空间偏导数的精度,但时间导数的精度仍然较低,容易引起较强的时间频散。
在有限差分求解时间导数方面,直接采用上述高阶格式对时间导数进行离散容易导致不稳定[12],但可以采用不同的空间导数组合实现基于Lax-Wendroff算法的声波方程时间高阶数值模拟[24]。本质上,Lax-Wendroff方案属于空间域方法,求解精度和效率有待进一步提高。相比之下,基于组合差分模板的时间—空间高阶差分法能够在兼顾效率的前提下有效提高时间模拟精度。在构建改进差分模板方面,Liu等[25]提出了菱形网格有限差分法求解二维拉普拉斯算子,提高了声波方程在时间—空间域同步任意偶数阶模拟精度。但是该菱形网格中时间和空间导数的差分算子必须保持一致,因此限制了灵活性和效率。Wang等[26]结合菱形网格与传统正交差分模板,发展了时间高阶差分算子与空间高阶差分算子相互独立的声波方程数值模拟算法,有效提高了计算效率。上述两种方案主要是针对形式较为简单的规则网格差分方法。Tan等[27]基于菱形模板的思想,将交错网格旁轴上的节点与轴向节点联合用于求解导数,提出了针对声波方程的时间四阶和六阶差分方案;胡自多等[28]对混合网格差分方法进行了推广与应用,提出了混合交错网格逆时偏移,有效提高了成像精度。通过构建组合差分模板的思想,目前已经发展了多种类型的时间—空间高阶有限差分方法,包括时间高阶弹性波差分[29]、优化时间高阶差分[30]、隐式时间高阶差分[31]、针对三维波动方程的时间高阶差分[32-33]等。但是,上述有限差分方法在构建改进模板时,主要采用正方形和立方体网格单元进行计算区域离散,即沿空间不同方向的离散网格间距一致,因此限制了模板的灵活性及进一步应用。
为了提高二维和三维声波方程时间—空间高阶有限差分数值模拟的灵活性,本文提出基于矩形/长方体网格单元(沿不同空间方向网格步长不一致)的改进时间—空间高阶有限差分法,分别用于求解二维和三维声波方程。基于平面波理论推导了相应的时间—空间域频散关系,进而应用泰勒展开求取了高阶差分系数。数值分析和多个模型算例验证了本文方法的有效性。
1 理论与方法 1.1 基于长方体网格单元的三维波动方程离散三维各向同性介质中常密度声波方程表达式为
| $ \frac{{\partial }^{2}P}{\partial {t}^{2}}={v}^{2}{\nabla }^{2}P $ | (1) |
式中:P=P(x, y, z, t)为声波波场;v=v(x, y, z, t)为介质速度;t为时间坐标;x、y和z为空间坐标;
采用有限差分法求解式(1)时,通常选用高阶差分格式对空间导数进行离散,即
| $ \begin{array}{l}{\nabla }^{2}{P}_{i,l,f}^{o}\approx \frac{1}{{h}_{x}^{2}}\left[{a}_{0}{P}_{i,l,f}^{o}+\sum\limits_{m=1}^{M}{a}_{m}\left({P}_{i+m,l,f}^{o}+{P}_{i-m,l,f}^{o}\right)\right]+\\ \frac{1}{{h}_{y}^{2}}\left[{a}_{0}{P}_{i,l,f}^{o}+\sum\limits_{m=1}^{M}{a}_{m}\left({P}_{i,l+m,f}^{o}+{P}_{i,l-m,f}^{o}\right)\right]+\\ \frac{1}{{h}_{z}^{2}}\left[{a}_{0}{P}_{i,l,f}^{o}+\sum\limits_{m=1}^{M}{a}_{m}\left({P}_{i,l,f+m}^{o}+{P}_{i,l,f-m}^{o}\right)\right]\end{array} $ | (2) |
式中:i、l、f表示空间坐标网格索引;o表示时间坐标网格索引;M为空间项差分算子长度的一半;am为空间域高阶差分系数[20];hx、hy和hz分别表示不同方向的空间网格步长。定义
| $ \left\{\begin{array}{l}{R}_{yx}=\frac{{h}_{y}}{{h}_{x}}\\ {R}_{zx}=\frac{{h}_{z}}{{h}_{x}}\end{array}\right. $ | (3) |
首选二阶形式对时间导数进行离散
| $ \frac{{\partial }^{2}{P}_{i,l,f}^{o}}{\partial {t}^{2}}\approx \frac{1}{{\left(\mathrm{\Delta }t\right)}^{2}}\left(-2{P}_{i,l,f}^{o}+{P}_{i,l,f}^{o-1}+{P}_{i,l,f}^{o+1}\right) $ | (4) |
式中Δt为时间步长。
采用传统方案(式(2)和式(4))对式(1)进行数值离散能够达到空间域高阶精度,但时间域精度较低。如图 1所示,将轴向坐标轴上的网格节点(三个坐标轴上的黑色节点)与非轴向网格节点(蓝色八面体所包含的空间节点)进行有效结合。在传统差分方案的基础上,构建组合差分模板,得到改进的时间导数离散差分格式
| $ \begin{array}{l}\frac{{\partial }^{2}{P}_{i,l,f}^{o}}{\partial {t}^{2}}\approx \frac{1}{\left(\mathrm{\Delta }{t}^{2}\right)}\left(-2{P}_{i,l,f}^{o}+{P}_{i,l,f}^{o-1}+{P}_{i,l,f}^{o+1}\right)-\\ \;\;\;\;\;\;\frac{{v}^{2}}{{h}_{x}^{2}}\left(\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{A}_{1}+\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-q}\sum\limits_{q=1}^{m-n}{A}_{2}\right)\end{array} $ | (5) |
| $ \begin{array}{l}{A}_{1}={d}_{m,n,0}\left({P}_{i+m,l+n,f}^{o}+{P}_{i-m,l+n,f}^{o}+{P}_{i+m,l-n,f}^{o}+{P}_{i-m,l-n,f}^{o}\right)+\\ {d}_{m,0,n}\left({P}_{i+m,l,f+n}^{o}+{P}_{i-m,l,f+n}^{o}+{P}_{i+m,l,f-n}^{o}+{P}_{i-m,l,f-n}^{o}\right)+\\ {d}_{0,m,n}\left({P}_{i,l+m,f+n}^{o}+{P}_{i,l-m,f+n}^{o}+{P}_{i,l+m,f-n}^{o}+{P}_{i,l-m,f-n}^{o}\right)\end{array} $ | (6) |
| $ \begin{array}{l}{A}_{2}={d}_{m,n,q}\left({P}_{i+m,l+n,f+q}^{o}+{P}_{i-m,l+n,f+q}^{o}+{P}_{i+m,l-n,f+q}^{o}+\right.\\ {P}_{i-m,l-n,f+q}^{o}+{P}_{i+m,l+n,f-q}^{o}+{P}_{i-m,l+n,f-q}^{o}+\\ \left.{P}_{i+m,l-n,f-q}^{o}+{P}_{i-m,l-n,f-q}^{o}\right)\end{array} $ | (7) |
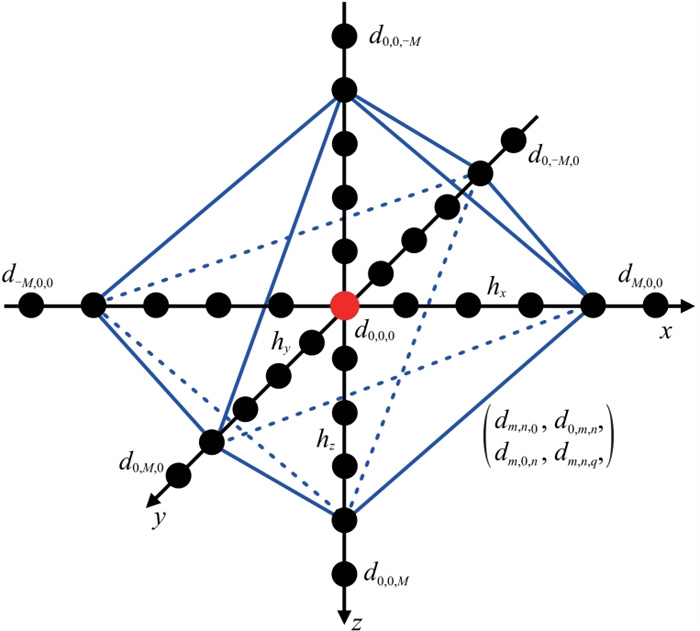
|
图 1 轴向与非轴向网格节点混合的改进时间高阶三维有限差分模板 红色圆点为待求节点,黑色圆点为轴向节点,蓝框所组成的八面体包含所有非轴向的节点,算子M为任意正整数。 |
式中:N为时间项差分算子长度的一半;dm, n, 0、dm, 0, n、d0, m, n和dm, n, q均为改进时间项离散格式中的高阶差分系数。式(5)的右端第一项为传统时间离散格式,A1项和A2项对应空间八面体上的节点,用于补偿传统时间离散格式的精度。
相应地,空间导数的离散格式修改为
| $ {\nabla }^{2}{P}_{i,l,f}^{o}\approx \frac{{v}^{2}}{{h}_{x}^{2}}\left({d}_{\mathrm{0,0},0}{P}_{i,l,f}^{o}+\sum\limits_{m=1}^{M}{A}_{3}\right) $ | (8) |
| $ \begin{array}{l}{A}_{3}={d}_{m,\mathrm{0,0}}\left({P}_{i+m,l,f}^{o}+{P}_{i-m,l,f}^{o}\right)+\\ {d}_{0,m,0}\left({P}_{i,l+m,f}^{o}+{P}_{i,l-m,f}^{o}\right)+\\ {d}_{\mathrm{0,0},m}\left({P}_{i,l,f+m}^{o}+{P}_{i,l,f-m}^{o}\right)\end{array} $ | (9) |
式(9)右端对应图 1中正交坐标轴上的节点;d0, 0, 0、dm, 0, 0、d0, m, 0和d0, 0, m为改进离散格式中的高阶差分系数。
将式(5)与式(8)结合,即可在时间域和空间域同步实现对式(1)的任意偶数阶精度差分求解。与前人成果不同,本文提出的时间高阶离散格式可以在不同方向采用非等间距的网格步长(
采用泰勒展开法对改进差分格式中的高阶系数进行求解。首先,基于平面波理论,标量波场P可表示为
| $ {P}_{i,l,j}^{o}={\mathrm{e}}^{i\left[{k}_{x}\left(x+i{h}_{x}\right)+{k}_{y}\left(y+l{h}_{y}\right)+{k}_{z}\left(z+f{h}_{z}\right)-\omega \left(t+o\mathrm{\Delta }t\right)\right]} $ | (10) |
式中:ω为角频率;kx、ky和kz分别为x、y和z方向的波数,且与总波数k之间具有如下关系
| $ \left\{\begin{array}{l}\omega =kv\\ {k}_{x}=k\mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{c}\mathrm{o}\mathrm{s}\varphi \\ {k}_{y}=k\mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{s}\mathrm{i}\mathrm{n}\varphi \\ {k}_{z}=k\mathrm{s}\mathrm{i}\mathrm{n}\theta \end{array}\right. $ | (11) |
式中:θ为从水平面测量的相对于垂向的平面波传播角度;ϕ为平面波方位角。
基于式(10)平面波解,将式(5)和式(8)代入式(1),可进一步化简整理为
| $ \begin{array}{l}{d}_{\mathrm{0,0},0}+2\sum\limits_{m=1}^{M}{A}_{4}+4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{A}_{5}+8\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{A}_{6}\\ \begin{array}{cc}& \end{array}={r}^{-2}\left[-2+2\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega \mathrm{\Delta }t\right)\right]\end{array} $ | (12) |
| $ \begin{array}{l}{A}_{4}={d}_{m,\mathrm{0,0}}\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)+{d}_{0,m,0}\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{y}{h}_{y}\right)+\\ {d}_{\mathrm{0,0},m}\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{z}{h}_{z}\right)\end{array} $ | (13) |
| $ \begin{array}{l}{A}_{5}={d}_{m,n,0}\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(n{k}_{y}{h}_{y}\right)+\\ \begin{array}{cc}& \end{array}{d}_{m,0,n}\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(n{k}_{z}{h}_{z}\right)+\\ \begin{array}{cc}& \end{array}{d}_{0,m,n}\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{y}{h}_{y}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(n{k}_{z}{h}_{z}\right)\end{array} $ | (14) |
| $ {A}_{6}={d}_{m,n,q}\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(n{k}_{y}{h}_{y}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(q{k}_{z}{h}_{z}\right) $ | (15) |
式中:
采用泰勒级数对上式中的余弦函数进行展开,可得
| $ \begin{array}{l}{d}_{\mathrm{0,0},0}+2\sum\limits_{m=1}^{M}\sum\limits_{j=0}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{j}{m}^{2j}}{\left(2j\right)!}{A}_{7}+\\ 4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}\sum\limits_{ε =0}^{\mathrm{\infty }}\sum\limits_{\delta =0}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{ε +\delta }{m}^{2ε }{n}^{2\delta }}{\left(2ε \right)!\left(2\delta \right)!}{A}_{8}+\\ 8\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{d}_{m,n,q}\sum\limits_{ε =0}^{\mathrm{\infty }}\sum\limits_{\delta =0}^{\mathrm{\infty }}\sum\limits_{\gamma =0}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{ε +\delta +\gamma }{m}^{2ε }{n}^{2\delta }{q}^{2\gamma }}{\left(2ε \right)!\left(2\delta \right)!\left(2\gamma \right)!}{A}_{9}\\ \approx 2\sum\limits_{j=1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{j}{r}^{2j-2}{\left(k{h}_{x}\right)}^{2j}}{\left(2j\right)!}\end{array} $ | (16) |
| $ {A}_{7}={d}_{m,\mathrm{0,0}}{k}_{x}^{2j}{h}_{x}^{2j}+{d}_{0,m,0}{k}_{y}^{2j}{h}_{y}^{2j}+{d}_{\mathrm{0,0},m}{k}_{z}^{2j}{h}_{z}^{2j} $ | (17) |
| $ \begin{array}{l}{A}_{8}={d}_{m,n,0}{k}_{x}^{2ε }{k}_{y}^{2\delta }{h}_{x}^{2ε }{h}_{y}^{2\delta }+{d}_{m,0,n}{k}_{x}^{2ε }{k}_{z}^{2\delta }{h}_{x}^{2ε }{h}_{z}^{2\delta }+\\ \begin{array}{cc}& \end{array}{d}_{0,m,n}{k}_{y}^{2ε }{k}_{z}^{2\delta }{h}_{y}^{2ε }{h}_{z}^{2\delta }\end{array} $ | (18) |
| $ {A}_{9}={k}_{x}^{2ε }{k}_{y}^{2\delta }{k}_{z}^{2\gamma }{h}_{x}^{2ε }{h}_{y}^{2\delta }{h}_{z}^{2\gamma } $ | (19) |
结合二项式定理
| $ \begin{array}{l}{k}^{2j}={\left({k}_{x}^{2}+{k}_{y}^{2}+{k}_{z}^{2}\right)}^{j}\\ =\sum\limits_{ε =0}^{j}\sum\limits_{\delta =0}^{ε }\frac{j!{k}_{x}^{2\left(j-ε \right)}{k}_{y}^{2\left(ε -\delta \right)}{k}_{z}^{2\delta }}{\left(j-ε \right)!\left(ε -\delta \right)!\delta !}\end{array} $ | (20) |
进一步将式(16)整理为
| $ \begin{array}{l}{d}_{\mathrm{0,0},0}+2\sum\limits_{m=1}^{M}\left({d}_{m,\mathrm{0,0}}+{d}_{0,m,0}+{d}_{\mathrm{0,0},m}\right)+\\ 4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}\left({d}_{m,n,0}+{d}_{m,0,n}+{d}_{0,m,n}\right)+\\ 8\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{d}_{m,n,q}+2\sum\limits_{m=1}^{M}\sum\limits_{j=1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{j}{m}^{2j}}{\left(2j\right)!}{A}_{10}{h}_{x}^{2j}+\\ 4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{A}_{11}+8\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{s=1}^{m-n}{d}_{m,n,q}{A}_{12}\\ \approx 2\sum\limits_{j=1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{j}{r}^{2j-2}}{\left(2j\right)!}{A}_{13}{h}_{x}^{2j}+\\ 2\sum\limits_{j=1}^{\mathrm{\infty }}\sum\limits_{ε =1}^{j-1}\frac{{\left(-1\right)}^{j}j!{r}^{2j-2}}{\left(2j\right)!\left(j-ε \right)!ε !}{A}_{14}{h}_{x}^{2j}+\\ 2\sum\limits_{j=1}^{\mathrm{\infty }}\sum\limits_{ε =1}^{j-1}\sum\limits_{\delta =1}^{ε -1}\frac{{\left(-1\right)}^{j}j!{r}^{2j-2}}{\left(2j\right)!\left(j-ε \right)!\left(ε -\delta \right)!\delta !}{A}_{15}{h}_{x}^{2j}\end{array} $ | (21) |
| $ {A}_{10}={d}_{m,\mathrm{0,0}}{k}_{x}^{2j}+{d}_{0,m,0}{k}_{y}^{2j}{R}_{yx}^{2j-2}+{d}_{\mathrm{0,0},m}{k}_{z}^{2j}{R}_{zx}^{2j-2} $ | (22) |
| $ \begin{array}{l}{A}_{11}={d}_{m,n,0}\sum\limits_{j=1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{j}\left({n}^{2j}{k}_{y}^{2j}{R}_{yx}^{2j}+{m}^{2j}{k}_{x}^{2j}\right)}{\left(2j\right)!}{h}_{x}^{2j}+\\ {d}_{m,0,n}\sum\limits_{j=1}^{\infty }\frac{{\left(-1\right)}^{j}\left({n}^{2j}{k}_{z}^{2j}{R}_{zx}^{2j}+{m}^{2j}{k}_{x}^{2j}\right)}{\left(2j\right)!}{h}_{x}^{2j}+\\ {d}_{0,m,n}\sum\limits_{j=1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{j}\left({n}^{2j}{k}_{z}^{2j}{R}_{zx}^{2j}+{m}^{2j}{k}_{y}^{2j}{R}_{yx}^{2j}\right)}{\left(2j\right)!}{h}_{x}^{2j}+\\ \sum\limits_{ε =1}^{\mathrm{\infty }}\sum\limits_{\delta =1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{ε +\delta }{m}^{2ε }{n}^{2\delta }}{\left(2ε \right)!\left(2\delta \right)!}{A}_{16}{h}_{x}^{2ε +2\delta }\end{array} $ | (23) |
| $ \begin{array}{l}{A}_{12}=\sum\limits_{j=1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{j}}{\left(2j\right)!}{A}_{17}{h}_{x}^{2j}+\\ \sum\limits_{ε =1}^{\mathrm{\infty }}\sum\limits_{\delta =1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{ε +\delta }}{\left(2ε \right)!\left(2\delta \right)!}{A}_{18}{h}_{x}^{2ε +2\delta }+\\ \sum\limits_{ε =1}^{\mathrm{\infty }}\sum\limits_{\delta =1}^{\mathrm{\infty }}\sum\limits_{\gamma =1}^{\mathrm{\infty }}\frac{{\left(-1\right)}^{ε +\delta +\gamma }{m}^{2ε }{n}^{2\delta }{q}^{2\gamma }}{\left(2ε \right)!\left(2\delta \right)!\left(2\gamma \right)!}{A}_{19}{h}_{x}^{2ε +2\delta +2\gamma }\end{array} $ | (24) |
| $ {A}_{13}={k}_{x}^{2j}+{k}_{y}^{2j}+{k}_{z}^{2j} $ | (25) |
| $ {A}_{14}={k}_{x}^{2j-2ε }{k}_{y}^{2ε }+{k}_{x}^{2j-2ε }{k}_{z}^{2ε }+{k}_{y}^{2j-2ε }{k}_{z}^{2ε } $ | (26) |
| $ {A}_{15}={k}_{x}^{2j-2ε }{k}_{y}^{2ε -2\delta }{k}_{z}^{2\delta } $ | (27) |
| $ \begin{array}{l}{A}_{16}={d}_{m,n,0}{k}_{x}^{2ε }{k}_{y}^{2\delta }{R}_{yx}^{2\delta }+{d}_{m,0,n}{k}_{x}^{2ε }{k}_{z}^{2\delta }{R}_{zx}^{2\delta }+\\ {d}_{0,m,n}{k}_{y}^{2ε }{k}_{z}^{2\delta }{R}_{yx}^{2ε }{R}_{zx}^{2\delta }\end{array} $ | (28) |
| $ {A}_{17}={m}^{2j}{k}_{x}^{2j}+{n}^{2j}{k}_{y}^{2j}{R}_{yx}^{2j}+{q}^{2j}{k}_{z}^{2j}{R}_{zx}^{2j} $ | (29) |
| $ \begin{array}{l}{A}_{18}={m}^{2ε }{n}^{2\delta }{k}_{x}^{2ε }{k}_{y}^{2\delta }{R}_{yx}^{2\delta }+{m}^{2ε }{q}^{2\delta }{k}_{x}^{2ε }{k}_{z}^{2\delta }{R}_{zx}^{2\delta }+\\ \begin{array}{cc}& \end{array}{n}^{2ε }{q}^{2\delta }{k}_{y}^{2ε }{k}_{z}^{2\delta }{R}_{yx}^{2ε }{R}_{zx}^{2\delta }\end{array} $ | (30) |
| $ {A}_{19}={k}_{x}^{2ε }{k}_{y}^{2\delta }{k}_{z}^{2\gamma }{R}_{yx}^{2\delta }{R}_{zx}^{2\gamma } $ | (31) |
比较式(21)两端关于
| $ \begin{array}{l}{d}_{\mathrm{0,0},0}+2\sum\limits_{m=1}^{M}\left({d}_{m,\mathrm{0,0}}+{d}_{0,m,0}+{d}_{\mathrm{0,0},m}\right)+\\ \begin{array}{cc}& \end{array}4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}\left({d}_{m,n,0}+{d}_{m,0,n}+{d}_{0,m,n}\right)+\\ \begin{array}{cc}& \end{array}8\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{d}_{m,n,q}=0\end{array} $ | (32) |
| $ \begin{array}{l}\sum\limits_{m=1}^{M}\frac{{\left(-1\right)}^{j}{m}^{2j}}{\left(2j\right)!}{A}_{20}+\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}\left[\frac{{\left(-1\right)}^{j}}{\left(2j\right)!}\left({d}_{m,n,0}{A}_{21}+\right.\right.\\ \left.\left.{d}_{m,0,n}{A}_{22}+{d}_{0,m,n}{A}_{23}\right)+\sum\limits_{ε =1}^{j-1}\frac{{\left(-1\right)}^{j}{m}^{2j-2ε }{n}^{2ε }}{\left(2j-2ε \right)!\left(2ε \right)!}{A}_{24}\right]+\\ 4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{d}_{m,n,q}\left[\frac{{\left(-1\right)}^{j}{A}_{25}}{\left(2j\right)!}+\sum\limits_{ε =1}^{j-1}\frac{{\left(-1\right)}^{j}{A}_{26}}{\left(2j-2ε \right)!\left(2ε \right)!}+\right.\\ \left.\sum\limits_{ε =1}^{j-1}\sum\limits_{\delta =1}^{ε -1}\frac{{\left(-1\right)}^{j}{m}^{2j-2ε }{n}^{2ε -2\delta }{q}^{2\delta }}{\left(2j-2ε \right)!\left(2ε -2\delta \right)!\left(2\delta \right)!}{A}_{27}\right]\\ \approx \frac{{\left(-1\right)}^{j}{r}^{2j-2}{A}_{28}}{\left(2j\right)!}+\sum\limits_{ε =1}^{j-1}\frac{{\left(-1\right)}^{j}j!{r}^{2j-2}{A}_{29}}{\left(2j\right)!\left(j-ε \right)!ε !}+\\ \sum\limits_{ε =1}^{j-1}\sum\limits_{\delta =1}^{ε -1}\frac{{\left(-1\right)}^{j}j!{r}^{2j-2}{A}_{30}}{\left(2j\right)!\left(j-ε \right)!\left(ε -\delta \right)!\delta !}\end{array} $ | (33) |
| $ {A}_{20}={d}_{m,\mathrm{0,0}}{k}_{x}^{2j}+{d}_{0,m,0}{k}_{y}^{2j}{R}_{yx}^{2j-2}+{d}_{\mathrm{0,0},m}{k}_{z}^{2j}{R}_{zx}^{2j-2} $ | (34) |
| $ {A}_{21}={n}^{2j}{k}_{y}^{2j}{R}_{yx}^{2j}+{m}^{2j}{k}_{x}^{2j} $ | (35) |
| $ {A}_{22}={n}^{2j}{k}_{z}^{2j}{R}_{zx}^{2j}+{m}^{2j}{k}_{x}^{2j} $ | (36) |
| $ {A}_{23}={n}^{2j}{k}_{z}^{2j}{R}_{zx}^{2j}+{m}^{2j}{k}_{y}^{2j}{R}_{yx}^{2j} $ | (37) |
| $ \begin{array}{l}{A}_{24}={d}_{m,n,0}{k}_{x}^{2j-2ε }{k}_{y}^{2ε }{R}_{yx}^{2ε }+{d}_{m,0,n}{k}_{x}^{2j-2ε }{k}_{z}^{2ε }{R}_{zx}^{2ε }+\\ \begin{array}{cc}& \end{array}{d}_{0,m,n}{k}_{y}^{2j-2ε }{k}_{z}^{2ε }{R}_{yx}^{2j-2ε }{R}_{zx}^{2ε }\end{array} $ | (38) |
| $ {A}_{25}={m}^{2j}{k}_{x}^{2j}+{n}^{2j}{k}_{y}^{2j}{R}_{yx}^{2j}+{q}^{2j}{k}_{z}^{2j}{R}_{zx}^{2j} $ | (39) |
| $ \begin{array}{l}{A}_{26}={m}^{2j-2ε }{n}^{2ε }{k}_{x}^{2j-2ε }{k}_{y}^{2ε }{R}_{yx}^{2ε }+\\ {m}^{2j-2ε }{q}^{2ε }{k}_{x}^{2j-2ε }{k}_{z}^{2ε }{R}_{zx}^{2ε }+\\ {n}^{2j-2ε }{q}^{2ε }{k}_{y}^{2ε }{k}_{z}^{2ε }{R}_{yx}^{2j-2ε }{R}_{zx}^{2ε }\end{array} $ | (40) |
| $ {A}_{27}={k}_{x}^{2j-2ε }{k}_{y}^{2ε -2\delta }{k}_{z}^{2\delta }{R}_{yx}^{2ε -2\delta }{R}_{zx}^{2\delta } $ | (41) |
| $ {A}_{28}={k}_{x}^{2j}+{k}_{y}^{2j}+{k}_{z}^{2j} $ | (42) |
| $ {A}_{29}={k}_{x}^{2j-2ε }{k}_{y}^{2ε }+{k}_{x}^{2j-2ε }{k}_{z}^{2ε }+{k}_{y}^{2j-2ε }{k}_{z}^{2ε } $ | (43) |
| $ {A}_{30}={k}_{x}^{2j-2ε }{k}_{y}^{2ε -2\delta }{k}_{z}^{2\delta } $ | (44) |
比较式(33)两端关于
| $ \begin{array}{l}\sum\limits_{m=1}^{M}{m}^{2j}{d}_{m,\mathrm{0,0}}+2\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{m}^{2j}\left({d}_{m,n,0}+{d}_{m,0,n}\right)+\\ \begin{array}{cc}& \end{array}4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{m}^{2j}{d}_{m,n,q}={r}^{2j-2}\end{array} $ | (45) |
| $ \begin{array}{l}\sum\limits_{m=1}^{M}{m}^{2j}{d}_{0,m,0}+2\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}\left({n}^{2j}{d}_{m,n,0}+{m}^{2j}{d}_{0,m,n}\right)+\\ \begin{array}{cc}& \end{array}4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{n}^{2j}{d}_{m,n,q}={R}_{yx}^{-2j}{r}^{2j-2}\end{array} $ | (46) |
| $ \begin{array}{l}\sum\limits_{m=1}^{M}{m}^{2j}{d}_{\mathrm{0,0},m}+2\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{n}^{2j}\left({d}_{m,0,n}+{d}_{0,m,n}\right)+\\ \begin{array}{cc}& \end{array}4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{q}^{2j}{d}_{m,n,q}={R}_{zx}^{-2j}{r}^{2j-2}\end{array} $ | (47) |
| $ \begin{array}{l}\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{m}^{2j-2ε }{n}^{2ε }{d}_{m,n,0}+2\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{m}^{2j-2ε }{n}^{2ε }{d}_{m,n,q}\\ =\frac{j!\left(2j-2ε \right)!\left(2ε \right)!{R}_{yx}^{-2ε }{r}^{2j-2}}{2\left(2j\right)!\left(j-ε \right)!ε !}\end{array} $ | (48) |
| $ \begin{array}{l}\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{m}^{2j-2ε }{n}^{2ε }{d}_{m,0,n}+2\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{m}^{2j-2ε }{n}^{2ε }{d}_{m,n,q}\\ =\frac{j!\left(2j-2ε \right)!\left(2ε \right)!{R}_{zx}^{-2ε }{r}^{2j-2}}{2\left(2j\right)!\left(j-ε \right)!ε !}\end{array} $ | (49) |
| $ \begin{array}{l}\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{m}^{2j-2ε }{n}^{2ε }{d}_{0,m,n}+2\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{m}^{2j-2ε }{n}^{2ε }{d}_{m,n,q}\\ =\frac{j!\left(2j-2ε \right)!\left(2ε \right)!{R}_{yx}^{2ε -2j}{R}_{zx}^{-2ε }{r}^{2j-2}}{2\left(2j\right)!\left(j-ε \right)!ε !}\end{array} $ | (50) |
| $ \begin{array}{l}\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{m}^{2j-2ε }{n}^{2ε -2\delta }{q}^{2\delta }{d}_{m,n,q}\\ =\frac{j!\left(2j-2ε \right)!\left(2ε -2\delta \right)!\left(2\delta \right)!{R}_{yx}^{2\delta -2ε }{R}_{zx}^{-2\delta }{r}^{2j-2}}{4\left(2j\right)!\left(j-ε \right)!\left(ε -\delta \right)!\delta !}\end{array} $ | (51) |
式中参数j、ε和δ的取值范围为
| $ \left\{\begin{array}{l}j\in \left[1,N\right]\\ j > ε > \delta \end{array}\right. $ | (52) |
综上所述,联合求解式(32)、式(45)~式(51),即可获得改进模板中的高阶差分系数d0, 0, 0、dm, 0, 0、d0, m, 0、d0, 0, m、dm, n, 0、dm, 0, n、d0, m, n和dm, n, q。表 1给出了改进差分模板中时间四阶差分系数,相关参数为M=6, N=2, r=0.36, Ryx=1.2, Rzx=1.5。将相应差分系数代入式(5)和式(8),即可实现三维地震波场高精度外推。
|
|
表 1 改进差分模板中时间四阶差分系数 |
二维常密度声波方程形式与方程(1)类似, 其中拉普拉斯算子的形式变为
基于图 2中所示差分模板,联合应用非轴向和轴向的网格节点二维声波方程中的时间导数和空间导数,得到改进的波场递推公式
| $ \begin{array}{l}\frac{1}{\left(\mathrm{\Delta }{t}^{2}\right)}\left(-2{P}_{i,l}^{o}+{P}_{i,l}^{o-1}+{P}_{i,l}^{o+1}\right)-\\ \frac{{v}^{2}}{{h}_{x}^{2}}\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{c}_{m,n}\left({P}_{i+m,l+n}^{o}+{P}_{i-m,l+n}^{o}+\right.\\ \left.{P}_{i+m,l-n}^{o}+{P}_{i-m,l-n}^{o}\right)\\ \approx \frac{{v}^{2}}{{h}_{x}^{2}}\left\{{c}_{\mathrm{0,0}}{P}_{i,l}^{o}+\left[{c}_{m,0}\left({P}_{i+m,l}^{o}+{P}_{i-m,l}^{o}\right)+\right.\right.\\ \left.{c}_{0,m}\left.\left({P}_{i,l+m}^{o}+{P}_{i,l-m}^{o}\right)\right]\right\}\end{array} $ | (53) |
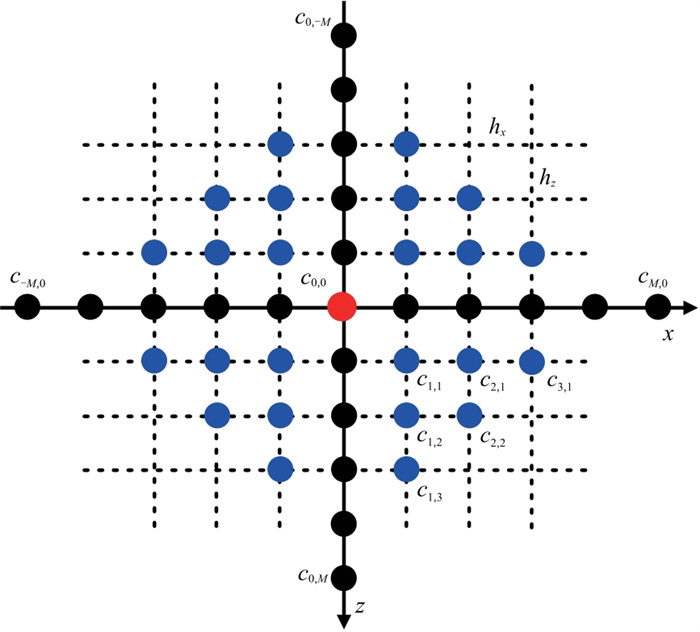
|
图 2 混合轴向与非轴向网格节点的改进时间高阶二维有限差分模板,算子M为任意正整数 |
式中c0, 0、cm, 0、c0, m和cm, n均为二维改进模板中差分系数。基于前文所述,结合平面波理论和泰勒级数展开即可求解二维改进差分格式中的高阶差分系数,此处不再赘述。
2 数值精度分析 2.1 相速度频散分析相速度相对误差是一种常用的评价有限差分数值精度的方法。通过计算不同差分方法的相速度相对误差值,对其精度进行对比、分析。为了简便起见,对相关方法进行了简写表示(表 2)。
|
|
表 2 不同差分方法及其简写 |
首先,定义参数
| $ \kappa =\frac{{v}_{\mathrm{F}\mathrm{D}}}{v}=\frac{1}{rk{h}_{x}}\mathrm{c}\mathrm{o}{\mathrm{s}}^{-1}\left({r}^{2}Q+1\right)-1 $ | (54) |
采用
| $ Q=\sum\limits_{m=1}^{M}{a}_{m}\left\{\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)-1\right]+{R}_{zx}^{-2}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{z}{h}_{z}\right)-1\right]\right\} $ | (55) |
对于MRFD-2D (2M, 2N)格式
| $ \begin{array}{l}Q=\sum\limits_{m=1}^{M}\left\{{c}_{m,0}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)-1\right]+{c}_{0,m}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{z}{h}_{z}\right)-1\right]\right\}+\\ 2\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{c}_{m,n}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(n{k}_{y}{h}_{y}\right)-1\right]\end{array} $ | (56) |
对于TFD-3D (2M, 2)格式
| $ \begin{array}{l}Q=\sum\limits_{m=1}^{M}{a}_{m}\left\{\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)-1\right]+\right.\\ \left.\begin{array}{cc}& \end{array}{R}_{yx}^{-2}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{y}{h}_{y}\right)-1\right]+{R}_{zx}^{-2}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{z}{h}_{z}\right)-1\right]\right\}\end{array} $ | (57) |
对于MCFD-3D (2M, 2N)格式
| $ \begin{array}{l}Q=\sum\limits_{m=1}^{M}\left\{{d}_{m,\mathrm{0,0}}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)-1\right]+\right.\\ \left.{d}_{0,m,0}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{y}{h}_{y}\right)-1\right]+{d}_{\mathrm{0,0},m}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{z}{h}_{z}\right)-1\right]\right\}+\\ 2\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}\left\{{d}_{m,n,0}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(n{k}_{y}{h}_{y}\right)-1\right]+\right.\\ \begin{array}{cc}& {d}_{m,0,n}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(n{k}_{z}{h}_{z}\right)-1\right]+\end{array}\\ \begin{array}{cc}& \left.{d}_{0,m,n}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{y}{h}_{y}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(n{k}_{z}{h}_{z}\right)-1\right]\right\}+\end{array}\\ 4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{q=1}^{m-n}{d}_{m,n,q}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(m{k}_{x}{h}_{x}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(n{k}_{y}{h}_{y}\right)\times \right.\\ \left.\mathrm{c}\mathrm{o}\mathrm{s}\left(q{k}_{z}{h}_{z}\right)-1\right]\end{array} $ | (58) |
采用均匀二维和三维模型(v=3000 m/s)测试不同方法的数值频散精度。图 3为Rzx=1.5时二维不同方法计算的相速度频散曲面,Δt=1.5 ms、hx=10 m。图 4为Ryx=1.2和Rzx=1.5时三维两种方法计算的相速度频散曲面,Δt=1.2 ms、hx= 10 m。由图可见,在相同的网格比和角度参数条件下,TFD-2D (16, 2)和TFD-3D (16, 2)计算的频散曲面远离参考平面,表明其存在较强频散误差。而MRFD-2D (16, 2N)和MCFD-3D (16, 2N)的计算结果与参考平面更接近,能够有效压制频散误差的干扰。此外,在改进差分方案中,随着算子N的增加,模拟精度得到了进一步提升。
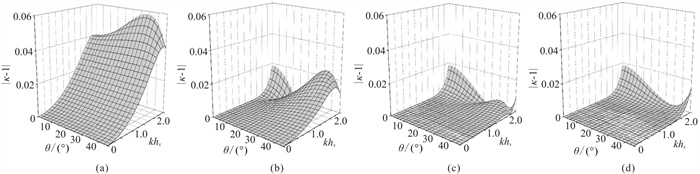
|
图 3 Rzx=1.5时二维均匀介质不同方法的频散曲面 (a)TFD-2D(16, 2);(b)MRFD-2D(16, 2);(c)MRFD-2D(16, 6);(d)MRFD-2D(16, 12) |
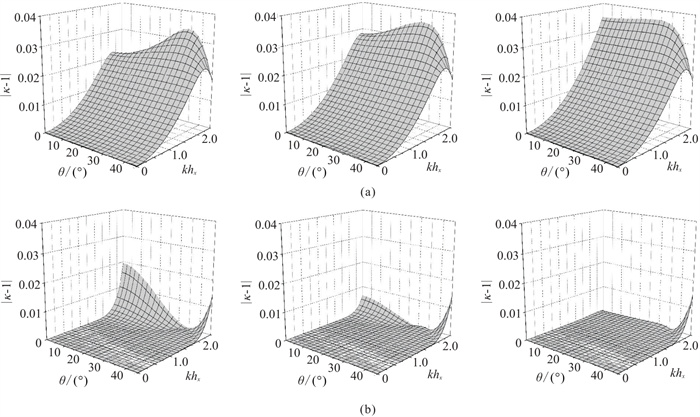
|
图 4 Ryx=1.2、Rzx=1.5时三维均匀介质两种方法的沿不同方位角的频散曲面 (a)TFD-3D(16, 2);(b)MCFD-3D(16, 8)。左、中、右分别为0、π/8、π/4。 |
稳定性条件是衡量有限差分方法优劣的一个重要因素。特征值分析通常被用于求解有限差分的稳定性因子[20, 25]。基于特征值分析得到不同差分方法中的库朗数r满足如下稳定性约束条件
| $ r\le s $ | (59) |
式中s为稳定性因子,其在不同差分方法中具有不同的计算形式,对于TFD-2D (2M, 2)格式
| $ s={\left\{\frac{\left(1+{R}_{zx}^{-2}\right)}{2}\sum\limits_{m=1}^{M}{a}_{m}\left[1+{\left(-1\right)}^{m-1}\right]\right\}}^{-\frac{1}{2}} $ | (60) |
对于MRFD-2D (2M, 2N)格式
| $ \begin{array}{l}s=\left\{\frac{1}{2}\sum\limits_{m=1}^{M}\left({c}_{m,0}+{c}_{0,m}\right)\left[1+{\left(-1\right)}^{m-1}\right]+\right.\\ {\left.\begin{array}{cc}& \end{array}\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}{c}_{m,n}\left[{\left(-1\right)}^{m+n-1}+1\right]\right\}}^{-\frac{1}{2}}\end{array} $ | (61) |
对于TFD-3D (2M, 2)格式
| $ s={\left\{\frac{\left(1+{R}_{yx}^{-2}+{R}_{zx}^{-2}\right)}{2}\sum\limits_{m=1}^{M}{a}_{m}\left[1+{\left(-1\right)}^{m-1}\right]\right\}}^{-\frac{1}{2}} $ | (62) |
对于MCFD-3D (2M, 2N)格式
| $ \begin{array}{l}s=\left\{\frac{1}{2}\sum\limits_{m=1}^{M}\left({d}_{m,\mathrm{0,0}}+{d}_{0,m,0}+{d}_{\mathrm{0,0},m}\right)\left[{\left(-1\right)}^{m-1}+1\right]+\right.\\ 2\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{N-m}\left({d}_{m,n,0}+{d}_{m,0,n}+{d}_{0,m,n}\right)\left[{\left(-1\right)}^{m+n-1}+1\right]+\\ {\left.4\sum\limits_{m=1}^{N-1}\sum\limits_{n=1}^{m-1}\sum\limits_{s=1}^{m-n}{d}_{m,n,l}\left[{\left(-1\right)}^{m+n+l-1}+1\right]\right\}}^{-\frac{1}{2}}\end{array} $ | (63) |
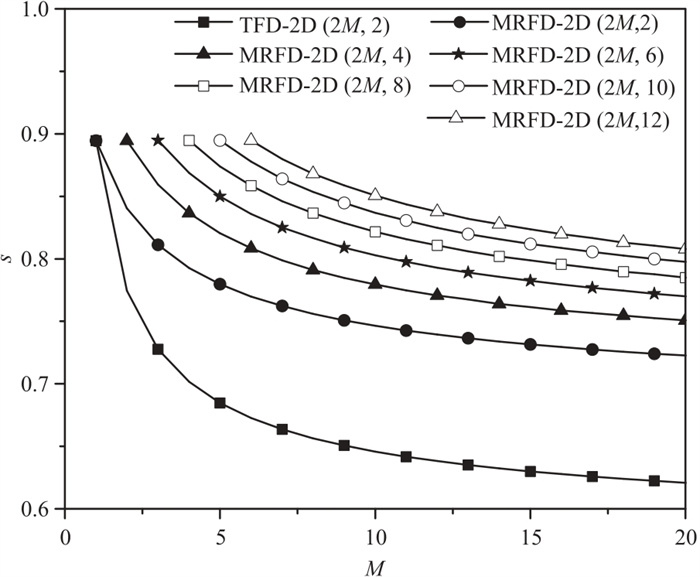
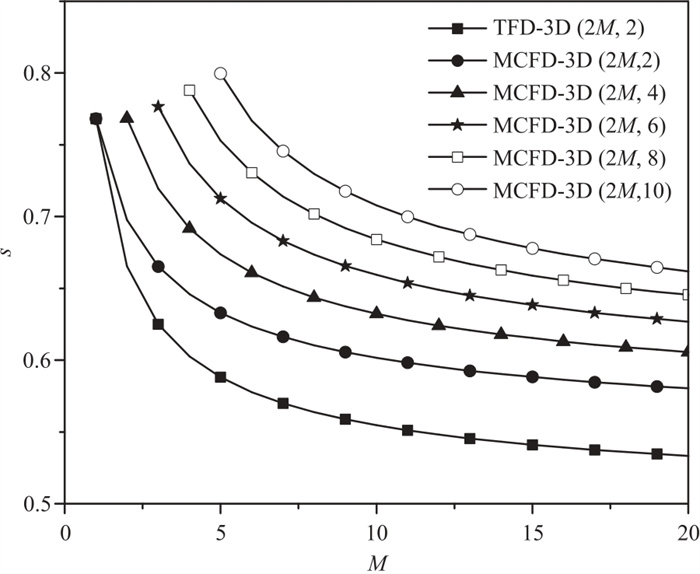
图 5、图 6为不同差分方案计算的二维和三维稳定性曲线图。从稳定性曲线对比结果可知:随着差分阶数(M)的增加,稳定性条件逐渐变差。当差分算子N长度一致时,相比之下,TFD-2D (2M, 2)和TFD-3D (2M, 2)具有最小的稳定性因子,表明传统方法容易出现不稳定。与传统方法相比,MRFD-2D (2M, 2N)和MCFD-3D(2M, 2N)具有更高的稳定性条件,因此当空间步长确定时可以选用更大的时间步长,有效提高计算效率。此外,稳定性随着N的增大而呈递增趋势。需要说明的是,图中的稳定性曲线均基于x方向的空间步长
|
图 5 Rzx=2.0时二维有限差分稳定性曲线对比 |
|
图 6 Ryx=1.5、Rzx=2.0时三维有限差分稳定性曲线对比 |
首先采用均匀模型对相关方法的数值精度进行测试。二维模型尺寸为4000 m×4800 m,矩形离散网格单元尺寸为10 m×12 m,介质速度为2800 m/s,震源采用为主频34 Hz的雷克子波。三维模型尺寸为2000 m×2400 m×2500 m,长方体离散网格单元尺寸为10.0 m×12.0 m×12.5 m,介质速度为2350 m/s,震源采用主频为25 Hz的雷克子波。震源均置于模型中央。
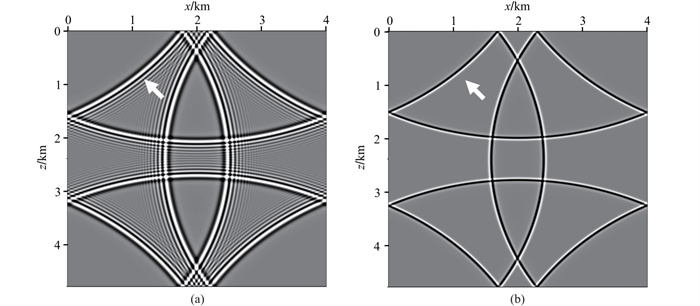
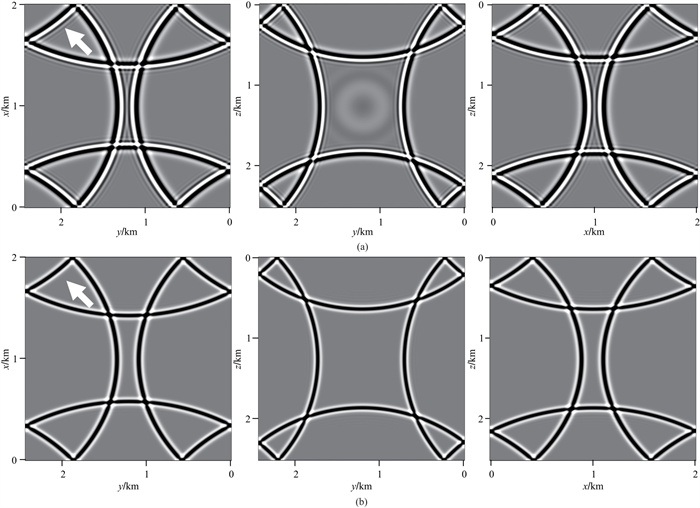
图 7和图 8分别为不同差分方法计算的均匀介质二维和三维波场切片。由图可见,传统时间二阶差分法(TFD-2D(16, 2)和TFD-3D(12, 2))计算的波场切片出现较强的时间频散误差干扰(如图中箭头所示)。相比之下,改进时间高阶差分法(MRFD-2D(16, 6)和MCFD-3D(12, 6))能够在保证空间模拟精度的前提下,显著降低时间频散误差。当模型参数一定时,改进差分方案在保证模拟精度的同时采用更大的时间步长,可以在一定程度上提高计算效率。
|
图 7 二维均匀模型Δt=2 ms时不同方法的波场切片对比 (a)TFD-2D(16, 2);(b)MRFD-2D(16, 6) |
|
图 8 三维均匀模型Δt=2 ms时不同方法的波场切片对比 (a)TFD-3D(12, 2);(b)MCFD-2D(12, 6) |
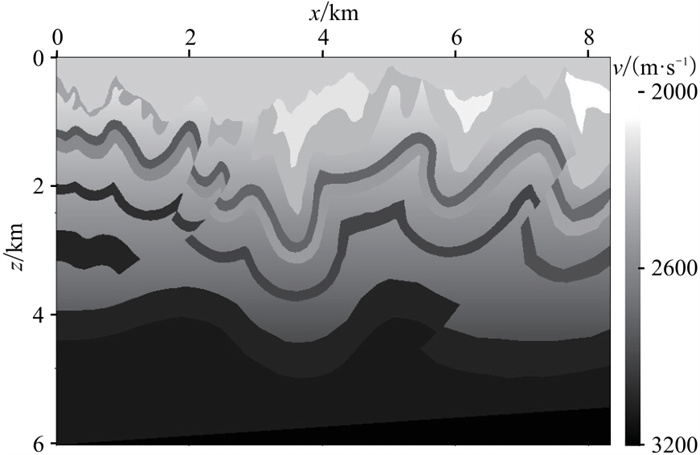
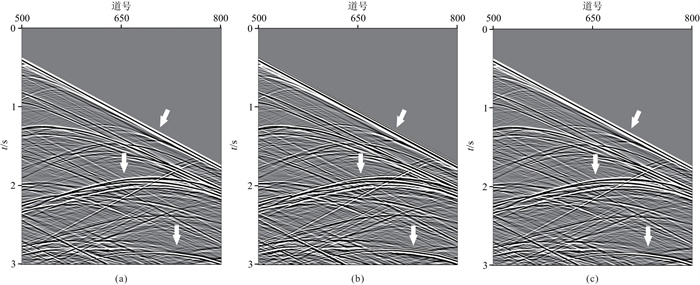
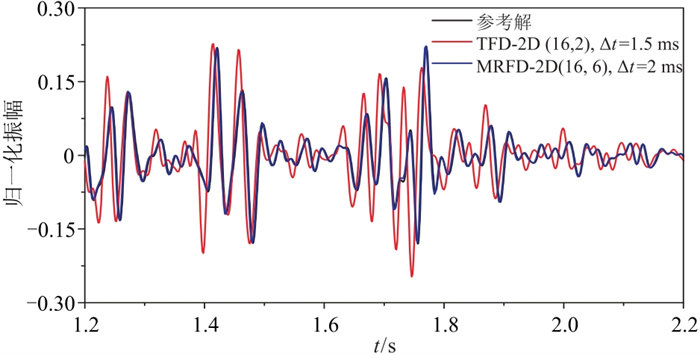
采用修改后的山麓模型对二维差分法的精度进行测试。如图 9所示,模型包含834×500个矩形网格单元,每个网格单元的尺寸为10 m×12 m。震源选用主频为28 Hz的雷克子波,置于(4170 m,120 m)。图 10a为传统方法采用较小时间步长计算出的参考地震记录局部显示,图 10b和图 10c分别为传统方法和改进方法采用大时间步长计算的局部地震记录,图 11为不同方法单道波形对比图。为了进一步凸显三维差分法在复杂模型正演中的优势,利用公式
|
图 9 二维山麓速度模型 |
|
图 10 山麓模型不同差分方法计算的局部地震记录对比 (a)参考解;(b)TFD-2D (16, 2), Δt=1.5 ms;(c) MRFD-2D (16, 6), Δt=2 ms |
|
图 11 山麓模型不同差分方法计算的单道波形对比 |

|
图 12 修改后的二维盐丘速度模型 |
|
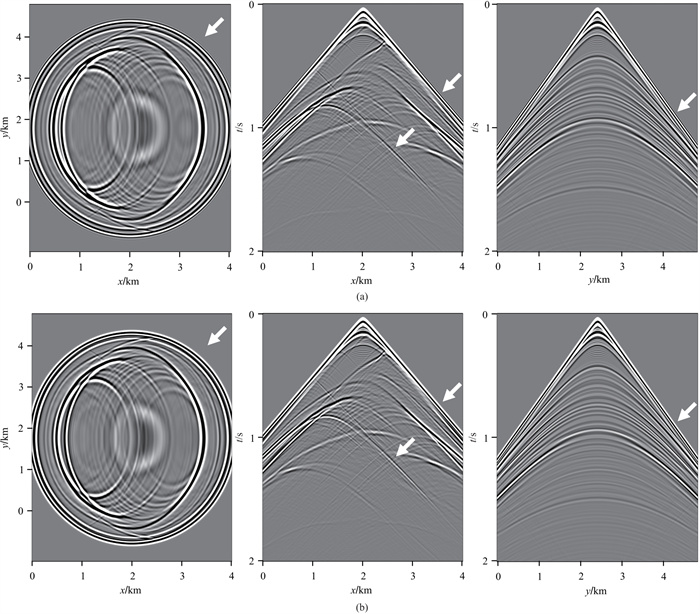
图 13 三维盐丘模型不同方法计算的地震记录对比 (a)TFD-3D (12, 2),Δt=1.6 ms;(b)MCFD-3D (12, 4),Δt=1.8 ms |
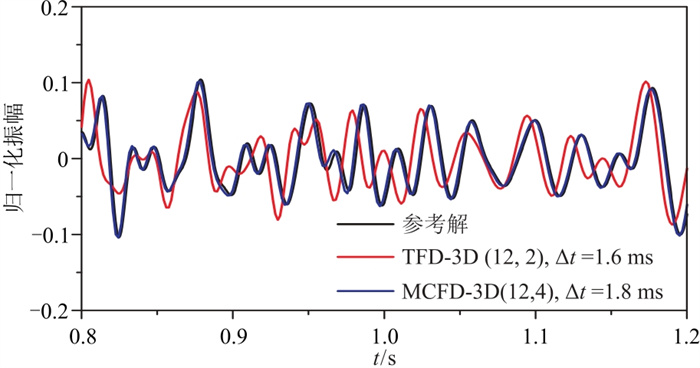
|
图 14 三维盐丘模型不同方法计算的单道波形对比 |
对比复杂模型不同方法计算的地震记录与单道波形可知,传统差分法(TFD-2D (16, 2)和TFD-3D (12, 2))采用相对较小的时间步长时仍然可以观察到比较明显的数值频散(如图中箭头所示),与参考波形存在较大相移误差。相比之下,当模型参数一致时,改进差分法(MRFD-2D (16, 6)和MCFD-3D (12, 4))采用相对较大的时间步长时单道记录与参考波形匹配较好,未出现明显数值频散。此外,在相同的计算平台上,改进方法能够采用更大的时间步长获得较高的模拟精度,既减少了迭代次数,又保证了计算效率。
综上所述,复杂模型算例表明,改进方案能够采用较大的时间步长和不一致的网格间距实现地震波场高精度数值模拟,证明了本文方法具有高效性和灵活性。
4 结论通过结合差分模板中旁轴节点和轴向节点,本文提出了一种基于矩形网格和长方体网格离散单元的改进时间—空间高阶有限差分方法,分别用于求解二维和三维声波方程。结合平面波解和泰勒级数展开求取了改进差分方案中的高阶时空域差分系数。
数值分析表明本文方法具有更高的相速度频散精度和稳定性。多个模型算例证明当模型参数相同时,改进差分方案能够在保证空间模拟精度的前提下有效提高时间模拟精度。此外,与传统方法相比,本文方法能够采用较大的时间步长和不同的网格间距,具有更高的效率和灵活性。
| [1] |
BAYSAL E, KOSLOFF D D, SHERWOOD J W C. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. |
| [2] |
VIRIEUX J. SH-wave propagation in heterogeneous media: velocity-stress finite difference method[J]. Geophysics, 1984, 49(11): 1933-1942. |
| [3] |
VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. |
| [4] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. |
| [5] |
董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419. DONG Liangguo, MA Zaitian, CAO Jingzhong, et al. A staggered-grid high-order difference method of one-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(3): 411-419. |
| [6] |
ZHANG Y, ZHANG H Z, ZHANG G Q. A stable TTI reverse time migration and its implementation[J]. Geophysics, 2011, 76(3): WA3-WA11. |
| [7] |
刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现[J]. 地球物理学报, 2010, 53(7): 1725-1733. LIU Hongwei, LI Bo, LIU Hong, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J]. Chinese Journal of Geophysics, 2010, 53(7): 1725-1733. |
| [8] |
李振春, 杨富森, 王小丹. 基于LS-RSGFD方法优化的横向各向同性(TI)介质一阶qP波高精度数值模拟[J]. 地球物理学报, 2016, 59(4): 1477-1490. LI Zhenchun, YANG Fusen, WANG Xiaodan. High-precision numerical simulation of first-order qP-waves in the transversely isotropic (TI) medium optimized by the LS-RSGFD method[J]. Chinese Journal of Geophysics, 2016, 59(4): 1477-1490. |
| [9] |
刘志强, 黄磊, 李钢柱, 等. 基于正交贴体网格的黏弹介质地震波模拟[J]. 石油地球物理勘探, 2023, 58(4): 839-846. LIU Zhiqiang, HUANG Lei, LI Gangzhu, et al. Numerical simulation of seismic waves in viscoelastic media based on orthogonal body-fitted grid[J]. Oil Geophysical Prospecting, 2023, 58(4): 839-846. |
| [10] |
SAENGER E H, GOLD N, SHAPIRO S A. Mode-ling the propagation of elastic waves using a modified finite-difference grid[J]. Wave Motion, 2000, 31(1): 77-92. |
| [11] |
刘财, 罗玉钦. 旋转时空双变网格有限差分地震波场正演模拟[J]. 地球物理学报, 2023, 66(9): 3840-3853. LIU Cai, LUO Yuqin. Modeling seismic wave propagation with rotated staggered dual-variable grid[J]. Chinese Journal of Geophysics, 2023, 66(9): 3840-3853. |
| [12] |
DABLAIN M A. The application of high-order differencing to the scalar wave equation[J]. Geophysics, 1986, 51(1): 54-66. |
| [13] |
LIU Y, SEN M K. An implicit staggered-grid finite-difference method for seismic modelling[J]. Geophysical Journal International, 2009, 179(1): 459-474. |
| [14] |
杜启振, 白清云, 李宾. 横向各向同性介质优化差分系数法地震波场数值模拟[J]. 石油地球物理勘探, 2010, 45(2): 170-176. DU Qizhen, BAI Qingyun, LI Bin. Optimized diffe-rence coefficient method seismic wave field numerical simulationin in vertical transverse isotropic medium[J]. Oil Geophysical Prospecting, 2010, 45(2): 170-176. |
| [15] |
王辉, 何兵寿, 邵祥奇. 一阶速度—胀缩—旋转弹性波方程交错网格数值模拟[J]. 石油地球物理勘探, 2022, 57(6): 1352‐1361. WANG Hui, HE Bingshou, SHAO Xiangqi. Numerical simulation of first-order velocity-dilatation-rotation elastic wave equation with staggered grid[J]. Oil Geophysical Prospecting, 2022, 57(6): 1352‐1361. |
| [16] |
陈亮, 黄建平, 王自颖, 等. 应用自适应变网格紧致差分的地震波数值模拟及逆时偏移[J]. 石油地球物理勘探, 2023, 58(3): 641-650, 712. CHEN Liang, HUANG Jianping, WANG Ziying, et al. Seismic numerical simulation and reverse time migration with adaptive variable-grid and compact difference method[J]. Oil Geophysical Prospecting, 2023, 58(3): 641-650, 712. |
| [17] |
LIU Y. Globally optimal finite-difference schemes based on least-squares[J]. Geophysics, 2013, 78(4): T113-T132. |
| [18] |
印兴耀, 刘博, 杨凤英. 一种基于全局优化的交错网格有限差分法[J]. 地震学报, 2015, 37(2): 278-288. YIN Xingyao, LIU Bo, YANG Fengying. A staggered grid finite difference method based on global optimization[J]. Acta Seismologica Sinica, 2015, 37(2): 278-288. |
| [19] |
方修政, 姚刚, 钮凤林, 等. 波场模拟有限差分参数优化选取[J]. 地球物理学报, 2023, 66(6): 2520-2533. FANG Xiuzheng, YAO Gang, NIU Fenglin, et al. Estimating optimal parameters of finite-difference scheme for wavefield modeling[J]. Chinese Journal of Geophysics, 2023, 66(6): 2520-2533. |
| [20] |
LIU Y, SEN M K. A new time-space domain high-order finite-difference method for the acoustic wave equation[J]. Journal of Computational Physics, 2009, 228(23): 8779-8806. |
| [21] |
梁文全, 杨长春, 王彦飞, 等. 用于声波方程数值模拟的时间—空间域有限差分系数确定新方法[J]. 地球物理学报, 2013, 56(10): 3497-3506. LIANG Wenquan, YANG Changchun, WANG Yanfei, et al. Acoustic wave equation modeling with new time-space domain finite difference operators[J]. Chinese Journal of Geophysics, 2013, 56(10): 3497-3506. |
| [22] |
JO C H, SHIN C, SUH J H. An optimal 9-point, finite-difference, frequency-space, 2D scalar wave extrapolator[J]. Geophysics, 1996, 61(2): 529-537. |
| [23] |
CHEN J B. An average-derivative optimal scheme for frequency-domain scalar wave equation[J]. Geophysics, 2012, 77(6): T201-T210. |
| [24] |
CHEN J B. A stability formula for Lax-Wendroff methods with fourth-order in time and general-order in space for the scalar wave equation[J]. Geophysics, 2011, 76(2): T37-T42. |
| [25] |
LIU Y, SEN M K. Time-space domain dispersion-relation-based finite-difference method with arbitrary even-order accuracy for the 2D acoustic wave equation[J]. Journal of Computational Physics, 2013, 232(1): 327-345. |
| [26] |
WANG E, LIU Y, SEN M K. Effective finite-difference modelling methods with 2-D acoustic wave equation using a combination of cross and rhombus stencils[J]. Geophysical Journal International, 2016, 206(3): 1933-1958. |
| [27] |
TAN S R, HUANG L J. An efficient finite-difference method with high-order accuracy in both time and space domains for modelling scalar-wave propagation[J]. Geophysical Journal International, 2014, 197(2): 1250-1267. |
| [28] |
胡自多, 刘威, 宋家文, 等. 速度—应力声波方程混合交错网格有限差分数值模拟及逆时偏移[J]. 石油地球物理勘探, 2023, 58(5): 1084-1100. HU Ziduo, LIU Wei, SONG Jiawen, et al. Mixed staggered grid finite difference numerical simulation and reverse time migration of velocity-stress acoustic equation[J]. Oil Geophysical Prospecting, 2023, 58(5): 1084-1100. |
| [29] |
REN Z, LI Z. Temporal high-order staggered-grid finite-difference schemes for elastic wave propagation[J]. Geophysics, 2017, 82(5): T207-T224. |
| [30] |
TAN S R, HUANG L J. A staggered-grid finite-difference scheme optimized in the time-space domain for modeling scalar-wave propagation in geophysical problems[J]. Journal of Computational Physics, 2014, 276: 613-634. |
| [31] |
REN Z, LI Z. High-order temporal and implicit spatial staggered-grid finite-difference operators for modelling seismic wave propagation[J]. Geophysical Journal International, 2019, 217(2): 844-865. |
| [32] |
XU S G, LIU Y. 3D acoustic wave modeling with a time-space-domain temporal high-order finite-difference scheme[J]. Journal of Geophysics and Engineering, 2018, 15(5): 1963-1976. |
| [33] |
胡自多, 刘威, 雍学善, 等. 三维波动方程时空域混合网格有限差分数值模拟方法[J]. 地球物理学报, 2021, 64(8): 2809-2828. HU Ziduo, LIU Wei, YONG Xueshan, et al. Mixed-grid finite-difference method for numerical simulation of 3D wave equation in the time-space domain[J]. Chinese Journal of Geophysics, 2021, 64(8): 2809-2828. |



 黄兴国, 吉林省长春市西民主大街938号吉林大学仪器科学与电气工程学院,130061。Email:
黄兴国, 吉林省长春市西民主大街938号吉林大学仪器科学与电气工程学院,130061。Email: