2. 大庆油田有限责任公司呼伦贝尔分公司, 黑龙江大庆 163712
2. Hulunbuir Subsidiary of PetroChina Daqing Oilfield Co. Ltd., Daqing, Heilongjiang 163712, China
目前中国油气地震勘探领域正逐渐向高精度、高分辨率、多尺度的方向发展,勘探目标更加复杂,对地震数据的处理要求也随之提高。然而,由于地表条件的限制,地震数据采集常常无法按照预定设计方案进行,需要消除各种障碍物、禁采区、海上拖缆羽状漂移现象以及废炮和废道等因素的影响。为了满足高精度、高分辨率、多尺度地震勘探的要求,野外地震数据采集需要以高密度、高维度、宽方位的方式进行,这无疑需要巨大的生产成本。而通过地震数据重建,可以以较低的计算成本获得高密度、规则的、宽方位的数据[1]。当前的地震数据重建方法主要分为三类:第一类是基于预测滤波的重建方法,通过设计滤波器对缺失地震数据重建。Fomel等[2]提出了流式预测误差滤波器,通过实时更新滤波系数,将预测方程与局部相似约束条件相结合,求解超定的线性系统,实现缺失数据的快速重建;吴庚等[3]提出高阶流式预测滤波重建方法,有效处理了包括近炮检距缺失情况在内的连续数据重建问题。第二类是基于稀疏变换的方法[4],也是目前的主流方法。以Donoho[5]提出的压缩感知理论为基础,将信号在某一变换域中稀疏表示,再用一个与稀疏变换基不相关的采样矩阵进行观测,将数据重建问题转换成求解约束最优化问题,以达到重建地震数据的目的。赵子越等[6]通过求取一组正交基函数与时间序列的内积,使原始信号呈现更强稀疏性,提出一种基于压缩感知技术的离散正交S变换的地震数据重建方法;段中钰等[7]提出了基于压缩感知的平方正则交替乘子方向算法的地震数据重建方法,具有较高的精度和实用性;董烈乾等[8]从快速迭代收缩阈值算法出发,提出了基于曲波变换的快速凸集投影算法,该算法保留了迭代收缩阈值算法的计算简单性,具有全局收敛速度快的优点[9-10]。第三类是基于机器学习的方法,其中深度学习在地震数据重建中具有自动调参、计算速度快等优点,是近年的研究热点。Chai等[11]提出了基于U-net卷积神经网络的地震数据重建方法,成功应用于规则缺失数据重建;冯永基等[12]发现普通GAN网络的重建结果常存在模糊、假频等现象,提出了融合部分卷积和注意力模型的改进GAN网络,显著提高了重建精度。此外,集成算法作为机器学习中的一个分支,抗噪能力强、样本抽样方式多样、泛化能力强、数据适应能力强,在地震数据重建方面也得到了应用。集成算法[13]按用途可分为三类:用于降低方差的Bagging法[14-15]、用于减少偏差的Boosting法[16]和用于提升预测结果精度的Stacking法[17]。Bagging法的基本思想是训练多个分类器,各个分类器之间不存在强依赖关系,然后把计算结果求平均值,随机森林算法是其典型代表;Boosting法的典型代表是AdaBoost、XGBoost算法,其原理是将多个弱模型组合成一个强模型,每个新模型都会基于上一个模型进行学习,并针对预测错误的样本进行重点训练。Stacking是把样本分成若干份,使用分类器对样本进行处理,处理结果作为下一层分类器的输入进行迭代。徐凯等[18]基于随机森林算法实现了地震数据重建;杨熙镭等[19]基于XGBoost算法对随机缺失含噪海上地震数据实现了高精度重建。XGBoost算法是Chen等[20]在梯度提升决策树(GBDT)算法的基础上提出的,具有计算速度快、预测精度高的优点,在众多领域也取得了较好的应用效果。闫星宇等[21]应用XGBoost算法建立了致密砂岩储层的孔隙度与渗透率回归预测模型;谷宇峰等[22]从优化参数角度出发,基于XGBoost算法建立了渗透率预测模型;张家臣等[23]基于XGBoost算法对渤海湾盆地测井曲线进行了重构。
本文基于XGBoost算法,以缺失地震道附近道号和数值构建回归关系,通过改变输入样本的尺寸和模式学习其中的回归关系,并重建地震数据。将该方法应用于正演模型数据和实际地震资料,均取得了较为理想的效果。
1 方法原理 1.1 基于XGBoost算法的缺失道重建 1.1.1 XGBoost算法的基本原理XGBoost算法是由陈天奇及其团队基于GBDT改进的Boosting算法,属于集成算法的一种。它通过多个弱学习器,按照权重组合成强学习器,具有训练快、预测精度高等优点[20]。
对于给定样本集D={(xi, yi)},其中xi为第i个样本的输入参数,yi为第i个样本输出目标值或真值,预测模型可表示为
| $ {\widehat{y}}_{i}=\sum\limits_{k=1}^{K}{f}_{k}\left({\boldsymbol{x}}_{i}\right)\;\;\;\;{f}_{k}\in \boldsymbol{F} $ | (1) |
式中:
XGBoost算法的核心原理是通过不断地特征分裂生成新的树,即一个新的函数,去拟合上次的预测残差。完成训练后,每棵树都会落到对应的叶子节点上,每个叶子节点都对应一个权重,最后将每棵树对应的权重加起来就是该样本的预测值。
在每次添加新树并进行拟合时,为了使目标函数尽量最小,XGBoost算法的目标函数中增加了正则化项用于控制树的复杂度,降低方差、防止过拟合。
XGBoost算法的整体目标函数为
| $ {E}^{\left(t\right)}=\sum\limits_{i=1}^{N}L\left[{y}_{i}, {\widehat{y}}_{i}^{\left(t\right)}\right]+\sum\limits_{k=1}^{K}\varOmega \left({f}_{k}\right) $ | (2) |
式中:t为迭代轮次;
由于XGBoost算法采用向前分步的方式进行迭代,以最大化降低目标函数为目的,在第t轮迭代后,目标函数更新为
| $ {E}^{\left(t\right)}=\sum\limits_{i=1}^{N}L\left[\begin{array}{c}{y}_{i}, {\widehat{y}}_{i}^{(t-1)}+{f}_{t}\left({\boldsymbol{x}}_{i}\right)\end{array}\right]+\varOmega \left({f}_{t}\right) $ | (3) |
每个
| $ \varOmega \left({f}_{k}\right)=\gamma T+\lambda \frac{1}{2}\sum\limits_{j=1}^{T}{\omega }_{j}^{2} $ | (4) |
式中:γ和λ为系数;T为叶子节点总数。
为了使XGBoost算法收敛更快且更精确,利用泰勒二阶展开对所有的二阶可导函数做近似替换。将每个数据的损失值相加,令
| $ \left\{\begin{array}{l}{g}_{i}=\frac{\partial L\left[{y}_{i}, {\widehat{y}}_{i}^{(t-1)}\right]}{\partial {\widehat{y}}_{i}^{(t-1)}}\\ {h}_{i}=\frac{{\partial }^{2}L\left[{y}_{i}, {\widehat{y}}_{i}^{(t-1)}\right]}{\partial {\left[{\widehat{y}}_{i}^{(t-1)}\right]}^{2}}\end{array}\right. $ | (5) |
| $ \left\{\begin{array}{l}{G}_{j}=\sum\limits_{i\in {\boldsymbol{I}}_{j}}{g}_{i}\\ {H}_{j}=\sum\limits_{i\in {\boldsymbol{I}}_{j}}{h}_{i}\end{array}\right. $ | (6) |
则可简化目标函数为[20]
| $ {E}^{\left(t\right)}\simeq \gamma T+\sum\limits_{j=1}^{T}\left[{G}_{j}{w}_{j}+\frac{1}{2}\left({H}_{j}+\lambda \right){w}_{j}^{2}\right] $ | (7) |
由于每个ωj都是独立的,对于上式以ωj作为函数的一元二次方程,当ωj=
| $ {\omega }_{j}^{\mathrm{*}}=-\frac{{G}_{j}}{{H}_{j}+\lambda } $ | (8) |
| $ {E}^{\mathrm{*}\left(t\right)}=-\frac{1}{2}\sum\limits_{j=1}^{T}\frac{{G}_{j}}{{H}_{j}+\lambda }+\gamma T $ | (9) |
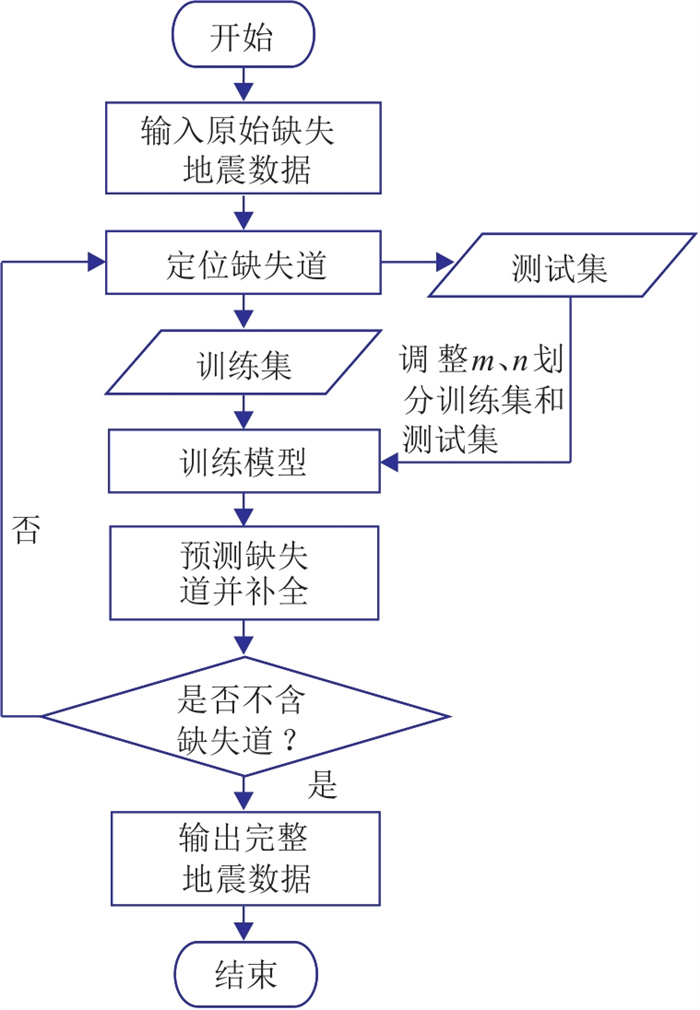
当前常用的重建方法如预测滤波法、各种稀疏变换方法,大多基于全部数据点进行全局处理。然而,在噪声干扰大的情况下,依赖所有数据点可能会将噪声和采集误差引入重建结果。实际上,对于缺失道中振幅补全结果产生实际贡献的仅仅是临近几道、一定时间范围内的数据点。因此,对于重建数据点(a, b),本文以该点的值Aa, b为学习目标,以周围若干数据点作为输入参数,用XGBoost算法构建回归模型,并将其运用在缺失道的补全。地震道缺失可分为单道缺失和多道缺失两种情况,补全的方法也分为两种。前者通过模型一次迭代就能重建出完整数据,后者则需要通过模型多次迭代才能恢复出完整数据。算法的具体流程如图 1所示。
|
图 1 缺失地震数据重建流程 |
(1) 单地震道缺失的补全。整个地震数据只有随机几道缺失且不连续,按缺失道将地震数据分成若干块,每块地震数据中只有一道缺失,在数据块中基于XGBoost算法构建回归方程进行缺失道的重建。对于中间地震道数据缺失的情况,在构建缺失地震道回归模型时,会将左、右两侧数据点的值纳入输入的特征属性中。具体来说,对于数据点(a, b),将左、右两侧各n道数据作为输入属性,以该点的预测值作为输出属性,建立特征属性集
| $ \begin{array}{l}{A}_{a, b}={F}_{1}({A}_{a\pm m, b-n}, \cdots , {A}_{a\pm m, b-1}, {A}_{a\pm m, b+1}, \cdots , \\ {A}_{a\pm m, b+n})\end{array} $ | (10) |
式中:
| $ {A}_{a, b}={F}_{2}({A}_{a\pm m, b+1}\cdots , {A}_{a\pm m, b+n}) $ | (11) |
当缺失道在最右侧时,则选择缺失道左侧邻近n道数据作为特征属性,即
| $ {A}_{a, b}={F}_{3}({A}_{a\pm m, b-n}, \cdots , {A}_{a\pm m, b-1}) $ | (12) |
式中F2、F3为学习器。
(2) 多道地震道缺失的补全。多道地震道缺失分为两种情况,一种是多道缺失而缺失道邻近两侧各n道完整,另一种是多道缺失且缺失道相邻n道也存在缺失,通常也称地震道连续缺失。对于前一种情况,可以看作是单道地震道缺失,综合采用F1、F2、F3这3个学习器进行一次迭代就能够重建出整个地震剖面。对于后一种情况,本文采用多次迭代的方式进行重建。首先对地震数据采用前一种方法进行一次重建,然后检查整个道集是否还存在缺失。如果有,则继续迭代,直到重建出完整的地震道集。
1.2 数据预处理和评价指标 1.2.1 数据预处理在常规的机器学习建模流程中,数据预处理是不可或缺的一步。这包括对数据进行清洗和转换等操作,旨在增强数据质量,从而优化模型训练后的效果。有些机器学习算法,如神经网络和支持向量机,对输入数据的数值范围敏感。当输入数据的数值范围相差较大,可能导致模型训练过程收敛速度较慢。因此,通过归一化处理,可以加快模型的收敛速度,提高训练效率。
本文在构建XGBoost回归模型前,先对地震单炮数据进行数据清洗,去除异常值,并把缺失地震道置0。然后采用归一化将数据缩放到0和1之间。
1.2.2 评价指标为了评估重建数据与真实数据之间的差异,本文实验选取均方根误差(RMSE)和峰值信噪比(PSNR)作为XGBoost回归模型的评价指标。RMSE定义为
| $ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{N}\sum\limits_{i=1}^{N}({\widehat{y}}_{i}-{y}_{i}{)}^{2}} $ | (13) |
一般来说,RMSE越小模型拟合效果越好。PSNR的定义为
| $ \mathrm{P}\mathrm{S}\mathrm{N}\mathrm{R}=20\times \mathrm{l}\mathrm{g}\frac{\mathrm{M}\mathrm{A}\mathrm{X}}{\sqrt{\frac{1}{N}\sum\limits_{i=1}^{N}({\widehat{y}}_{i}-{y}_{i}{)}^{2}}} $ | (14) |
式中MAX为
应用模型数据和实际单炮记录的随机缺失验证XGBoost算法的重建效果。在模型数据实验中,通过不断改变m、n的取值,比较重建后单炮与原始单炮,找到最佳重建效果的m、n取值方案,再用到实际数据的重建。
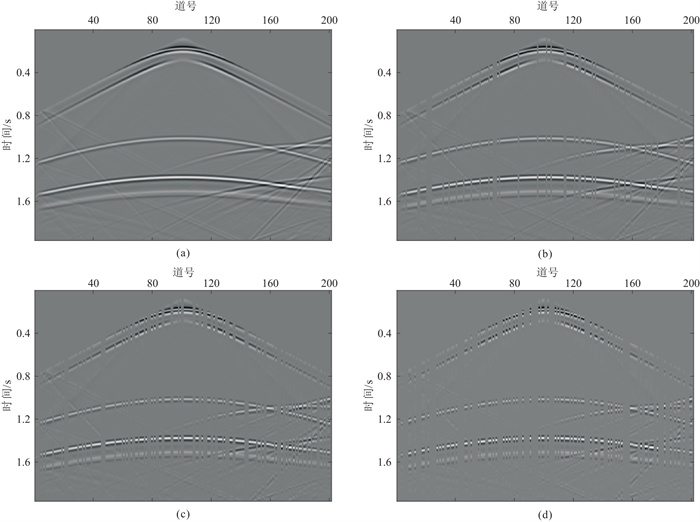
2.1 输入样本尺寸对重建效果的影响在地震数据重建过程中,由于对缺失道的补全结果产生实际贡献的仅仅是临近道、有限时间范围内的数据点,样本输入尺寸对重建效果有很大影响。为了探究这一问题,本文应用模型生成的单炮记录进行实验。采用波动方程有限差分法对三层速度模型进行单炮正演模拟,获得了201×982个样点的单炮记录(图 2a),其中时间采样间隔为2 ms。
|
图 2 三层模型正演单炮记录(a)及20%(b)、40%(b)、60%(c)随机地震道缺失后的单炮记录 |
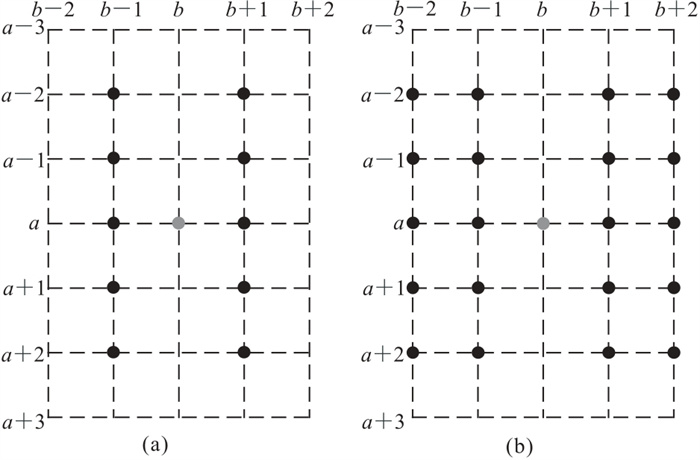
首先对模拟的单炮记录振幅做归一化处理。然后再人工进行20%、40%、60%的随机地震道缺失(图 2b~图 2d)。将缺失地震道全部填充为0,并通过调整m、n的值进行缺失道重建。样本输入方式如图 3所示。
|
图 3 m=2、n=1(a)和m=2、n=2(b)时缺失数据补全输入点示意图 灰点表示需重建的样本点;黑点表示输入样本点。 |
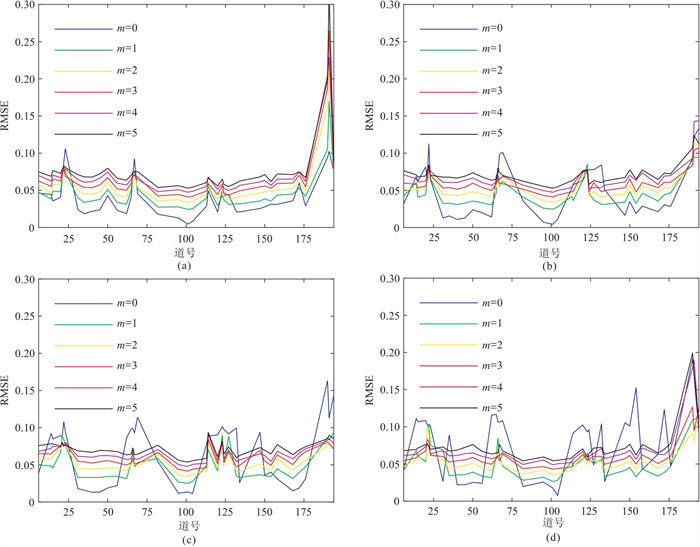
在使用XGBoost进行地震道重建时,输入过多的采样点会增大运算负担,甚至引入噪声。因此,参数m和n的选择要谨慎。过大的m值可能导致缺失道的开头和尾部部分数据点无法重建,而过大的n值在缺失地震道太多时会增加迭代次数,甚至无法完成地震道重建。因此,考虑到模型单炮记录的维度,本文对模型测试中m、n进行分组取值,分别测试不同组合(n取1、2、3、4,m取0、1、2、3、4、5)的重建效果。在地震道20%随机缺失情况下,不同m、n组合重建后的RMSE如图 4所示。由图 4可知:在单道缺失情况下,图中表现为平缓折线,m取值小单道重建效果好,但过小又在时间方向上输入样本不足,表现为平缓折线在连续缺失处出现突变(如图 4中蓝线所示);而n应该取稍微大一点的值,尽量保证在临近道上学习到足够多的样本特征而不影响迭代精度。这样的参数选择策略有助于在保持计算效率的同时提高地震道重建的精度。
|
图 4 模型数据缺失20%情况下n=1(a)、2(b)、3(c)、4(d)而m取不同值时重建地震道的RMSE对比 |
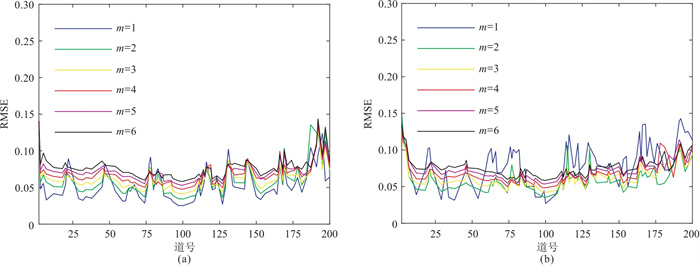
当地震道连续缺失时,图 4中显示的剧烈波动处(如第23、68、120和195道附近)表明,由于连续道重建的输入样本本身就是经过重建后的数据,因此不可避免地带有误差,导致连续道重建后均方根误差比较大。此时,n的取值不易过大或过小,太小会造成输入样点不足,而过大会引入噪声,造成数据整体误差变大。在图 4的第195道处,随n不断变大折线整体波动更加剧烈。随着地震道缺失程度的增加,n取值越大,地震道连续缺失的地方折线波动越剧烈,重建误差越大(图 5)。这时m应取值大一些,以保证时间方向上尽量更多地输入、学习到足够的特征。
|
图 5 模型数据缺失40%情况下n取1(a)或2(b)而m取不同值时重建地震数据的RMSE对比 |
综合考虑以上因素,对于模型数据,当缺失40%以上时,连续道缺失较多,n取值应小一些,m取值大一些,采用20~35个输入样本进行重建效果最好;当缺失40%以下时,单道缺失较多,n取值应稍大,m取值小一点,采用15~25个输入样本进行重建效果最好。总之,连续道缺失占比较高时,n取值应小一些,m取值大一些,反之亦然。
2.2 不同缺失程度重建效果分析针对不同缺失程度,选择合适的m、n值,在XGBoost中训练模型,得到缺失20%、40%、60%情况下的地震单炮记录重建结果。与基于凸集投影的Curvelet算法(方法一)和U-net网络(方法二)的重建结果对比以验证本文方法的有效性。
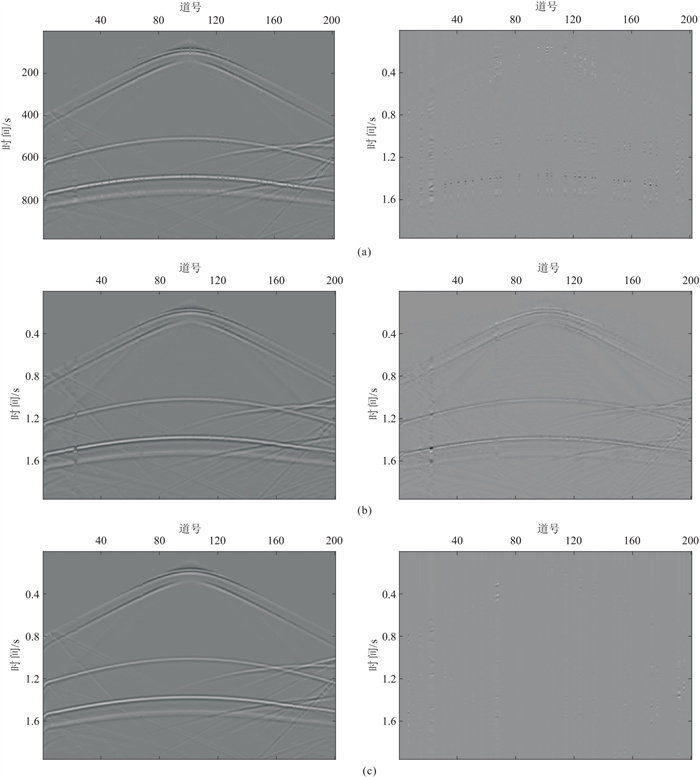
在随机缺失20%情况下,对比图 6左的重建道集,可以看出,三种方法均能恢复各同相轴的细节,效果都较好。然而,对比图 6右重建残差道集,可以看出,方法一和方法二重建残差中都存在同相轴残留,说明丢失了部分有效信息,而基于XGBoost算法(本文方法)的重建残差比较随机,有效信号非常弱,重建效果明显优于前两种方法。
|
图 6 模型数据缺失20%情况下三种方法重建的单炮(左)及残差(右) (a)方法一;(b)方法二;(c)本文方法 |
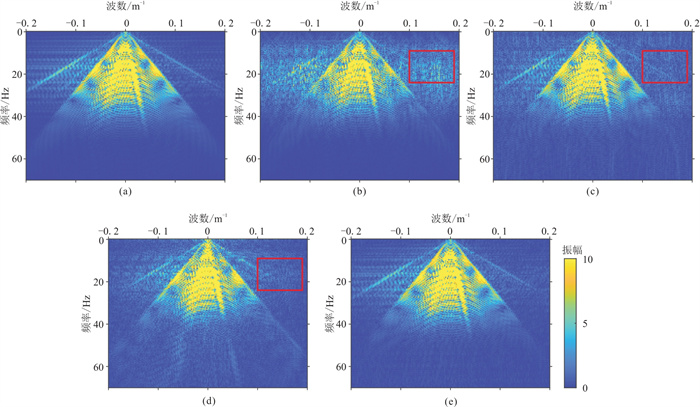
由于地震道缺失后会在频率域引入噪声,在F-K谱上会出现频散现象,表现为杂乱像素点(图 7b)。方法一和方法二重建的F-K谱频散现象虽然大大减弱,但在红框内还是有很弱的残留(图 7c、图 7d),而本文方法的重建地震数据F-K谱(图 7e)与原始数据的F-K谱(图 7a)最接近,表明本文方法的频散消除效果最好。
|
图 7 模型数据随机缺失20%情况下三种方法重建结果的F-K谱对比 (a)原始单炮;(b)20%随机缺失单炮;(c)方法一的重建单炮;(d)方法二的重建单炮;(e)本文方法的重建单炮 |
表 1统计了在随机地震道缺失20%情况下三种方法重建结果的RMSE,可见,本文方法的表现也要优于其他两种方法,说明XGBoost算法在地震数据重建中具有巨大应用潜力。
|
|
表 1 20%随机缺失情况下三种方法重建的RMSE统计 |
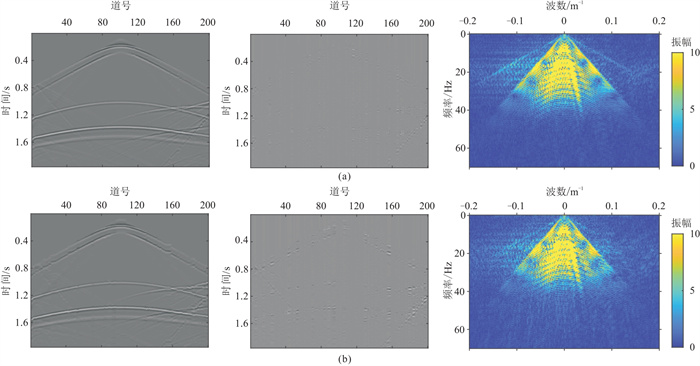
在随机缺失40%和60%情况下,本文方法的重建结果如图 8所示。当随机缺失40%时,重建结果中同相轴细节都比较清晰,几条细小的同相轴也能恢复(图 8a左),残差的同相轴趋势较弱(图 8a中),频散现象也较弱(图 8a右),重建效果较好。而当随机缺失60%时,重建结果中同相轴细节有小部分丢失,但能较好恢复缺失部分的趋势(图 8b左),残差的同相轴趋势较明显(图 8b中),频散现象较明显(图 8b右),重建效果一般。
|
图 8 模型数据随机缺失40%(a)和60%(b)情况下本文方法重建的单炮记录(左)、残差(中)及F-K谱(右)对比 |
川西坳陷油气资源丰富,勘探、开发程度相对较低,具有广阔的勘探前景。由于川西坳陷地表与地质构造复杂、多变,给地震数据的采集带来了不小的挑战。在单炮地震记录中具体表现为,时常会出现弱道、坏道以及50 Hz高压线干扰等,在一定程度上影响了地震数据的高精度成像。因此,缺失道数据的重建就显得至关重要。川西实际单炮记录共300道,每道2002个样点,采样间隔为2 ms,其中第24、38、34、50、51、78、99、129、166、179、182、195、211、234道(共计14道)为缺失道或弱道。由于实际资料缺失道数相对较少,实验中先删除了这些缺失道和弱道,然后采用XGBoost算法进行重建,以验证算法的可行性。再对其余若干道进行随机缺失删除,以提高缺失率,从而探究本文方法在不同缺失程度下对实际资料的重建效果。
与模型数据相比,实际资料单炮记录更复杂,同相轴更多,波形更多变。对于模型数据,当缺失40%以上(连续缺失较多)时,输入样本为20~35个样点的重建效果最好;当缺失40%以下(单道缺失情况较多)时,输入样本为15~25个样点的重建效果最好。实际资料中同相轴的数量约为模拟单炮的10~18倍。因此,在实际资料处理中,选择了150~450个点作为输入样本。
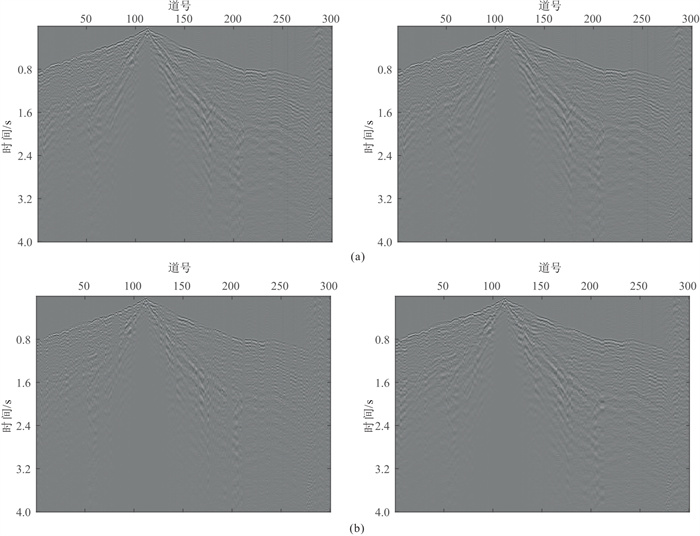
对于缺失5%实际地震道集(图 9a左),本文方法重建结果中同相轴连续,较好地恢复了缺失道(图 9a右)。对于缺失30%实际地震道集(图 9b左),连续缺失的出现机率变大,重建效果不佳,这可由第110、第210道附近同向轴连续性较差得到印证(图 9b)。
|
图 9 实际资料缺失5%(a)与人为缺失30%(b)的单炮记录(左)及本文方法重建结果(右)的对比 |
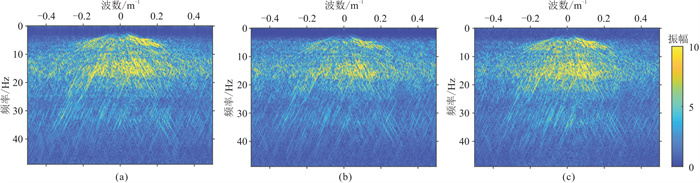
在缺失30%的情况下,计算原始单炮、缺失单炮及本文方法重建单炮的F-K谱如图 10所示,可见,重建后的图像与原始图像非常接近,基本没有引入额外噪声,这充分证明了XGBoost算法在随机道缺失地震数据重建中的有效性。
|
图 10 实际资料单炮(a)、缺失率30%后单炮(b)与本文方法重建单炮(c)的F-K谱对比 |
最后,对缺失单炮记录和重建后的单炮记录计算峰值信噪比,结果如表 2所示。由表 2可以看出,在缺失率小于30%情况下,重建能提高道集的峰值信噪比,m、n的取值也较符合经验总结,进一步说明了本文基于XGBoost算法的地震数据重建方法的有效性。
|
|
表 2 不同缺失率实际道集及重建后的峰值信噪比对比 |
基于集成算法的优点,本文提出了一种基于XGBoost算法的随机缺失地震数据重建方法。该方法从局部学习的角度出发,通过建立缺失地震道附近道号与数值构建回归关系重建地震数据。针对不同类型的地震道缺失情况,通过改变输入样本的数量和使用不同学习器,从而更精确地学习回归关系并重建地震数据。模拟单炮实验结果表明,基于XGBoost算法的随机缺失地震道的重建效果优于基于凸集投影的Curvelet算法和U-net网络。实际数据处理结果验证了本文方法的有效性。
值得注意的是,在实际资料中,地震道的缺失往往更多样,地震道连续缺失和地震道非连续缺失会同时出现,m、n选取更困难。如何应优化算法获得最佳的m和n取值组合,从而提高地震数据重建的精度,是今后进一步的研究方向。
| [1] |
黄炜霖. 勘探地震数据表征与重构研究进展[C]. 中国地球科学联合学术年会论文集, 2020, 66-67. HUANG Weilin. Advances in characterization and reconstruction of exploration seismic data[C]. Proceedings of the China Earth Science Joint Conference, 2020, 66-67. |
| [2] |
FOMEL S, CLAERBOUT J. Streaming prediction-error filters[C]. SEG Technical Program Expanded Abstracts, 2016, 35: 4787-4791.
|
| [3] |
吴庚, 刘财, 刘殿秘, 等. 连续缺失地震数据的高阶流式预测滤波插值方法[J]. 地球物理学报, 2023, 66(3): 1220-1231. WU Geng, LIU Cai, LIU Dianmi. et al, Seismic data interpolation beyond continuous missing data using high order streaming prediction filter[J]. Chinese Journal of Geophysics, 2023, 66(3): 1220-1231. |
| [4] |
ZHAO H, YANG T, NI Y D, et al. Reconstruction method of irregular seismic data with adaptive thresholds based on different sparse transform bases[J]. Applied Geophysics, 2021, 18(3): 345-360. |
| [5] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. |
| [6] |
赵子越, 李振春, 张敏. 利用压缩感知技术的离散正交S变换地震数据重建[J]. 石油地球物理勘探, 2020, 55(1): 29-35. ZHAO Ziyue, LI Zhenchun, ZHANG Min. Seismic data reconstruction using discrete orthonormal S-transform based on compressive sensing[J]. Oil Geophysical Prospecting, 2020, 55(1): 29-35. |
| [7] |
段中钰, 李婷婷, 肖勇, 等. 基于压缩感知的SR-ADMM地震数据重建[J]. 石油地球物理勘探, 2021, 56(6): 1220-1228. DUAN Zhongyu, LI Tingting, XIAO Yong, et al. Seismic data reconstruction by SR-ADMM algorithm based on compressed sensing[J]. Oil Geophysical Prospecting, 2021, 56(6): 1220-1228. |
| [8] |
董烈乾, 张慕刚, 汪长辉, 等. 应用快速POCS算法的非均匀地震数据重建[J]. 石油地球物理勘探, 2023, 58(2): 334-339. DONG Lieqian, ZHANG Mugang, WANG Changhui, et al. Reconstruction of non‑uniformly sampled seismic data based on fast POCS algorithm[J]. Oil Geophysical Prospecting, 2023, 58(2): 334-339. |
| [9] |
易继东, 张敏, 李振春, 等. 深度学习地震数据重建方法研究综述[J]. 地球物理学进展, 2023, 38(1): 361-381. YI Jidong, ZHANG Min, LI Zhenchun, et al. Review of deep learning seismic data reconstruction methods[J]. Progress in Geophysics, 2023, 38(1): 361-381. |
| [10] |
郑浩, 张兵. 基于卷积神经网络的智能化地震数据插值技术[J]. 地球物理学进展, 2020, 35(2): 721-727. ZHENG Hao, ZHANG Bing. Intelligent seismic data interpolation via convolutional neural network[J]. Progress in Geophysics, 2020, 35(2): 721-727. |
| [11] |
CHAI X T, GU H M, LI F, et al. Deep learning for irregularly and regularly missing data reconstruction[J]. Scientific Reports, 2020, 10(1): 3302-3320. |
| [12] |
冯永基, 陈学华. 融合部分卷积和注意力机制对抗网络模型的地震数据重建[J]. 石油地球物理勘探, 2023, 58(1): 21-30. FENG Yongji, CHEN Xuehua. Reconstruction of seismic data by fusing partial convolution and attention mechanism adversarial network models[J]. Oil Geophysical Prospecting, 2023, 58(1): 21-30. |
| [13] |
岳中文, 闫逸飞, 王煦, 等. 基于随钻数据的岩性识别机器学习算法研究进展[J]. 科学技术与工程, 2023, 23(10): 4044-4057. YUE Zhongwen, YAN Yifei, WANG Xu, et al. Research progress of machine learning algorithm for lithology identification based on data while drilling[J]. Science Technology and Engineering, 2023, 23(10): 4044-4057. |
| [14] |
BREIMAN L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140. |
| [15] |
BREIMAN L. Random forest[J]. Machine Learning, 2001, 45(10): 5-32. |
| [16] |
FRIEDMAN J. Greedy function approximation: a gradient boosting machine[J]. Annals of Statistics, 2001, 29(5): 1189-1232. |
| [17] |
WOLPERT D H. Stacked generalization[J]. Neural Networks, 1992, 5(2): 241-259. |
| [18] |
徐凯, 孙赞东. 基于随机森林方法的地震插值方法研究[J]. 石油科学通报, 2016, 3(1): 22-31. XU Kai, SUN Zandong. Seismic interpolation based on a random forest method[J]. Petroleum Science Bulletin, 2016, 3(1): 22-31. |
| [19] |
杨熙镭, 黄华, 吴树梁, 等. 基于XGBoost算法的地震数据重构研究[C]. 大数据与地球物理——第十六届国家安全地球物理专题研讨会, 2020, 97-102. YANG Xilei, HUANG Hua, WU Shuliang, et al. Research on seismic data reconstruction based on XGBoost algorithm[C]. Big Data and Geophysics: The 16th National Security Geophysics Symposium, 2020, 97-102. |
| [20] |
CHEN T Q, GUESTRIN C. XGBoost: A scalable tree boosting system[C]. Proceedings of the ACM SIGKDD 22nd ACM SIGKDD International Conference on Know‑ledge Discovery and Data Mining, 2016, 785-794.
|
| [21] |
闫星宇, 顾汉明, 肖逸飞, 等. XGBoost算法在致密砂岩气储层测井解释中的应用[J]. 石油地球物理勘探, 2019, 54(2): 447-455. YAN Xingyu, GU Hanming, XIAO Yifei, et al. XGBoost algorithm applied in the interpretation of tight-sand gas reservoir on well logging data[J]. Oil Geophysical Prospecting, 2019, 54(2): 447-455. |
| [22] |
谷宇峰, 张道勇, 鲍志东. 测井资料PSO-XGBoost渗透率预测[J]. 石油地球物理勘探, 2021, 56(1): 26-37. GU Yufeng, ZHANG Daoyong, BAO Zhidong. Permeability prediction using PSO-XGBoost based on logging data[J]. Oil Geophysical Prospecting, 2021, 56(1): 26-37. |
| [23] |
张家臣, 邓金根, 谭强, 等. 基于XGBoost的测井曲线重构方法[J]. 石油地球物理勘探, 2022, 57(3): 697-705. ZHANG Jiachen, DENG Jingen, TAN Qiang, et al. Reconstruction of well logs based on XGBoost[J]. Oil Geophysical Prospecting, 2022, 57(3): 697-705. |



 田仁飞, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院,610059。Email:
田仁飞, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院,610059。Email: