0 引言

作为多波多分量地震勘探主体的转换波(P-SV)地震勘探技术越来越受到地球物理学界的重视，该技术能够提供较纵波勘探更多的地层岩性信息，并可解决流体识别、裂隙预测、储层识别和含气性预测等热点问题。其中P-SV静校正仍是难题之一，难点在于横波静校正量的求取。与纵波相比，横波不受空隙和流体影响，其低速带通常比潜水面深，受地形起伏、裂隙及低速带的强烈影响，并且在地表浅层横波速度通常远小于纵波速度，在同一位置横波静校正量通常是纵波静校正量的2~10倍^[1-3]。因此，常规的纵波静校正方法难以满足P-SV静校正的要求。在资料处理过程中，如果不做横波(或接收点)静校正，而直接进行剩余静校正，则较大的剩余静校正量易使校正结果出现不稳定的“周波跳跃”现象。

针对P-SV静校正问题，学者们进行了很多研究。Armin^[4]提出利用共接收点(Common Receiver Point，CRP)道集拾取纵、横波折射初至建立表层横波速度模型，求解横波静校正量，可解决长波长静校正量问题，但是需要拾取纵、横波折射初至；杨海申等^[5]引进纵、横波延迟信息，建立表层横波速度模型，从而求取横波静校正量，但其假设纵、横波折射层相同，且一定程度上依赖纵波模型，因此该方法同样具有局限性；Caary等^[6]在假设地下结构比较平缓，且CRP叠加剖面信噪比高的情况下，通过优化CRP叠加道相干法求取横波短波长静校正量；赵秀莲等^[7]用理论模型和实际资料对Caary的方法进行了验证，表明该方法的效果明显优于常规方法，且稳定性较好；潘树林等^[8]对CRP叠加道集相关算法进行了改进，在考虑地下构造形态的基础上，利用已知的纵波叠加剖面确定某层构造形态后，再按照CRP叠加道相干法获得某检波点的静校正量，适用于构造较复杂地区；孟小红等^[9]利用瑞利面波频散特征反演低降速带横波速度结构，从而得到横波静校正量，但并未验证其可靠性和实用性；蔡露曦等^[10]利用F-K变换和谱分析方法对面波静校正处理技术进行了改进，能够将横波速度结构的横向分辨率提高到道间距水平，实际应用中有较好潜力；曲寿利^[11]提出超密度地震技术，试图通过提高地震数据的空间采样密度，获得高质量地震数据提高地表静校正、去噪、近地表速度建模的精度等，但只是一种设想，能否成功还有待进一步探索和实践。以上这些方法均有相应的应用条件及各自的优、缺点。

在二维地震勘探中，由于受野外施工条件、成本和项目效益等诸多因素限制，地震记录的野外采集道间距往往较大。由于瑞利面波的速度很低，记录中的高频成分容易产生空间假频，在面波频谱中出现因空间假频造成的假象，这对提取野外实际地震记录中的瑞利面波频散信息的可靠性和精度造成影响。因此，本文在借鉴孟小红等^[9]的方法原理基础上，提出利用小波变换对大道距采样记录进行时空插值，以提高P-SV资料中瑞利面波频散高频信息的精度，从而提高反演表层横波速度结构精度，进而求取P-SV的横波静校正量，并用理论模型和实际数据进行了验证计算。

1 小波变换实现地震道间插值 1.1 小波插值基本原理

小波分析是一种在时间—频率域的分析方法，介于纯时间域的方波分析和纯频率域的傅里叶分析之间，同时在时间域和频率域均有良好的局部化性质。随信号的不同，不同频率成分在时(空)域上的采样步长具有调节性，即频高者密、频低者疏。

小波变换基本原理^[12-13]是信号在分辨率为$ {2}^{-m-1} $处的近似部分可通过分辨率为$ {2}^{-m} $处的近似部分和细节部分的小波重构得到，其中m为信号分解层数。将原始信号$ {c}_{0} $看成是分辨率为$ {2}^{0} $的空间的近似部分，如果该空间的细节部分可以忽略或估计，那么分辨率为$ {2}^{-1} $的空间近似信号就可由原始信号得到。

已知数据$ {c}_{0} $和小波$ \left\{\varPhi \left({2}^{-j}k-n\right),\varPsi \left({2}^{-j}k-n\right)\right\} $(其中Φ为尺度函数；Ψ为对应小波函数；j为尺度函数宽度，其值越大尺度函数越窄，对应小波频率越高；n为输入信号长度；k为比例常数，即尺度函数平移的位置，j和k均为整数。)，$ {\varPhi }_{jn} $，$ {\varPsi }_{jn} $满足容许性条件，那么$ {c}_{0} $在分辨率为$ {2}^{-j} $空间中的近似部分$ {c}^{j} $和细节部分$ {d}^{j} $可表示为

$ {c}_{k}^{j}=\sum\limits_{n}{c}_{n}^{j-1}h\left(n-2k\right) $

(1)

$ {d}_{k}^{j}=\sum\limits_{n}{c}_{n}^{j-1}g\left(n-2k\right) $

(2)

式中：$ h\left(n\right) $是低通滤波器，且$ h\left(n-2k\right)=〈{\varPhi }_{jk,}{\varPhi }_{j-1n}〉 $，$ 〈•,•〉 $表示内积；$ g\left(n\right) $是高通滤波器，且$ \mathrm{g}\left(n-2k\right)=〈{\varPhi }_{jk,}{\varPsi }_{j-1n}〉 $。它们是正交镜像滤波器(QMF)。反变换可以表示为

$ \begin{array}{l}{c}_{n}^{j-1}=\sum\limits_{k}{c}_{k}^{j}〈{\varPhi }_{j-1n},{\varPhi }_{jk}〉+\\ \sum\limits_{k}{d}_{k}^{j}〈{\varPhi }_{j-1n},{\varPsi }_{jk}〉\end{array} $

(3)

则

$ {c}_{n}^{-1}=\sum\limits_{k}{c}_{k}^{0}〈{\varPhi }_{-1n},{\varPhi }_{0k}〉+\sum\limits_{k}{d}_{k}^{0}〈{\varPhi }_{-1n},{\varPsi }_{0k}〉 $

(4)

式(4)就是插值公式，其中$ {c}_{k}^{0} $是已知的，而$ {d}_{k}^{0} $是未知的。

获取$ {d}_{k}^{0} $的具体方法有两种：

方法一：由式(4)可知，如果分辨率为$ {2}^{0} $空间的细节部分可以忽略，即$ {d}_{k}^{0}=0 $，那么可得

$ {c}_{n}^{-1}=\sum\limits_{k}{c}_{k}^{0}〈{\varPhi }_{-1n},{\varPhi }_{0k}〉 $

(5)

在大多数情况下，$ {d}_{k}^{0} $是可以忽略的。此时，信号通过插值增加信息量是一个有效的处理过程。

方法二：如果$ {d}_{k}^{0} $不能忽略，此时就需进行估值。因为它包含了信号$ {c}_{n}^{-1} $的高频成分。在地震剖面上，对于某一道数据，可认为高波数与低波数部分的波形是相似的。它们的不同之处在于频率，高波数部分的频率要高。

因此，$ {d}_{k}^{0} $可以通过下述步骤获得：

(1) 将低波数空间的信号进行高通滤波；

(2) 对于某一道数据，根据某些变化方法，从步骤(1)得到的高频成分中估计$ {d}_{k}^{0} $；

(3) 循环进行下一道，重复步骤(1)和步骤(2)。

由于利用方法二得到的$ {d}_{k}^{0} $会包含一些不真实的信息并且实现复杂，因此，本文采用方法一，选取db4小波为母小波。

1.2 插值效果分析

小波插值是同时对时间和空间进行插值，而在地震插值中主要关心道间插值。因此，在二维插值试验中舍弃时间方向的插值数据，只考虑道间插值。

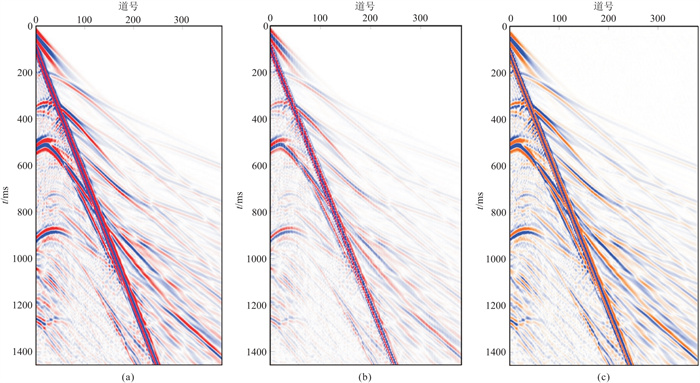
如图 1a为理论模拟的地震浅层记录，其时间采样率为0.5 ms，道间距为2 m，记录道数为384道。将图 1a均匀抽道为时间采样率0.5 ms，道间距为4 m、记录道数192道后，使用db4小波做2倍道内插，插值后记录如图 1c所示，并与图 1a比较，图 1c与图 1a基本相同，没有出现背景噪声及空间假频现象，同相轴的连续性仍好，说明该方法具有较高的精度。

图 2a为某地区野外实际获得的单炮大时空采样地震记录，时间采样率为1 ms，道间距为50 m，记录道数264道。通过小波插值方法将图 2a进行4倍道内插后的结果如图 2b所示，时间采样率为1 ms，道间距为12.5 m，插值后道数为1056道。由图可见，图 2b保持了图 2a同相轴的连续性，并且未见出现背景噪声及空间假频等现象。

2 瑞利面波频率—速度谱变化

瑞利面波是一种沿固体自由界面下约一个波长深度范围内传播的弹性波，其勘探深度约为1/2波长。它在非均匀介质(如层状介质)中传播存在频散现象。层状介质瑞利面波频散与介质密度、层厚度、纵波速度、横波速度有关，其中横波速度和层厚对频散的影响最大，其他因素的影响相对较小，因此，瑞利面波频散曲线常用于反演介质横波速度。而面波的反演主要是基于频散曲线的反演，如果通过对面波数据插值可提高频率—速度谱的信噪比，那么对频散曲线的提取是非常有利的。

目前频散曲线提取的主要算法有互相关法^[14-15]、频率—波数法^[16-17]、f-p变换算法^[18]、τ-p变换算法^[19-21]和基于高分辨率线性拉东变换法、多重信号分类法、多重滤波法、非线性信号相似性分析法、频率—贝塞尔法^[22-24]等。本文采用τ-p变换算法。对于均匀介质，在t-x域中时距曲线为直线的面波和抛物线的反射波在τ-p域中分别为一个点和一个椭圆，据此特性就可得到频散曲线。其基本原理为：首先对原始数据做倾斜叠加(即线性拉东变换)，将数据变换到慢度—截距域(p-τ)；其次，沿截距$ \tau $方向做一维傅里叶变换得到慢度—频率域(p-f)数据；最后将慢度转换成速度即可获得速度—频率域(v-f)数据。

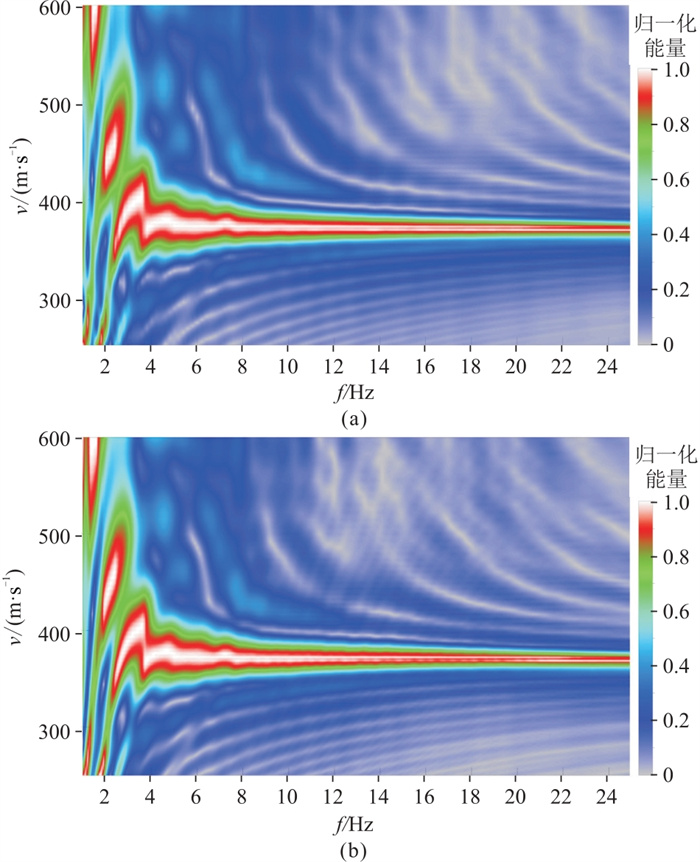
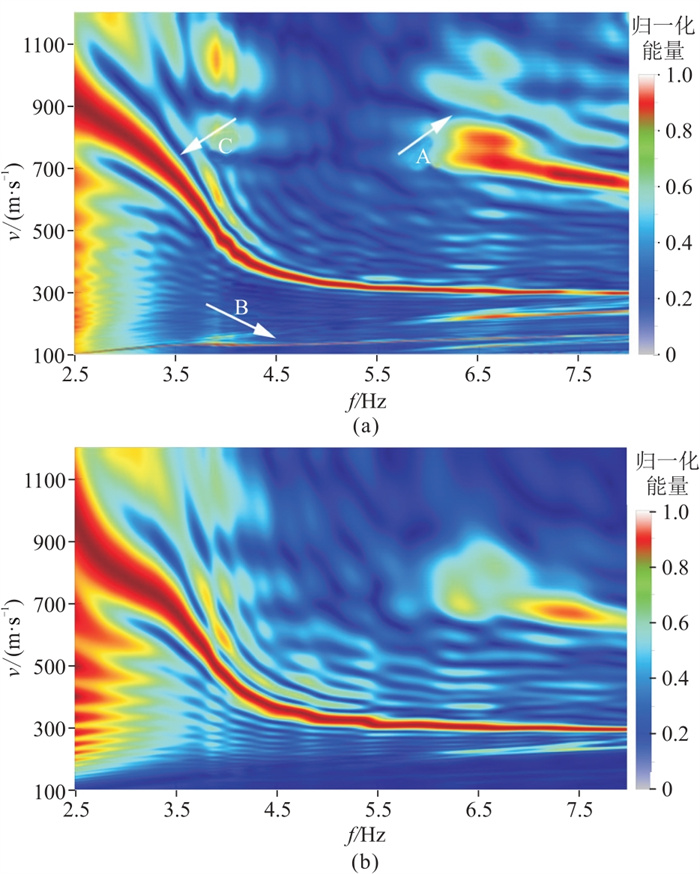
图 3a和图 3b分别为图 1a和图 1c对应的频率—速度谱。从图中可以看出图 3a、图 3b基本相同，主能量团基本没有发生变化，有效频率范围大约都在2~24 Hz。由于模型数据的面波频散程度较小，求取的频散曲线随频率的增大，速度呈减小趋势不是很明显，该结果验证了小波插值的可靠性。图 4是对图 2进行频谱分析得到的频率—速度谱。由图可见，道间插值后获取的频率—速度谱(图 4b)的基阶频散曲线的拐点更清晰(箭头C处)，能量团较插值前(图 4a)更强，同时，高频段高速区频散曲线的能量更集中(箭头A处)，对箭头B处的低速区域的噪声干扰也有明显压制。图 4说明，本文的插值方法可以对面波信息进行有效插值，并且能够提高其频率—速度谱的信噪比。

3 瑞利面波频散曲线反演

目前，层状介质瑞利面波频散曲线的反演算法包括全局非线性反演法和局部线性反演法。全局非线性反演法，如遗传算法、遗传粒子群算法^[25]、蜻蜓算法^[26]、闪电连接过程优化算法^[27]等，虽然能明显降低对初始模型的依赖，但计算量大，反演速度慢；局部线性反演算法，如阻尼最小二乘法，对给定的初始模型的依赖性较强，但反演速度快。因此在地震勘探中可通过地震折射资料较准确地获得浅层地质界面位置信息，故本文选用阻尼最小二乘法进行反演。具体过程如下：

(1) 给定初值：根据实测频散曲线的变化规律，做出定性解释，即确定可能的层数及各层的横波速度和厚度的变化范围，选择反演开始时各层横波速度v和厚度l的初值，即建立一个初始地层模型；

(2) 将步骤(1)的初始地层模型的理论频散曲线与实测瑞利波频散曲线比较，求得它们之间的偏差δ₀；

(3) 利用阻尼最小二乘方法调整初始地层模型的参数，重新计算调整后的地层模型的理论频散曲线，再与实测频散曲线比较，得到新的偏差δ_M，其中M为迭代次数；

(4) 重复上述过程，反复调整地层模型参数，使得理论频散曲线不断逼近实测频散曲线，直至δ_M小于给定的偏差阈值δ_g为止，其中g为目标阈值代号。

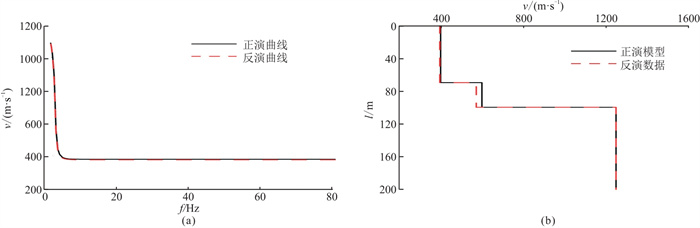
给定的理论模型数据为一个三层均匀层状介质模型。表 1列出了理论模型的各层介质参数；表 2列出了理论模型各层横波速度和层厚度以及最小二乘法初始模型数据和反演模型的各层横波速度和层厚度。图 5a显示了阻尼最小二乘法频散曲线反演结果与理论模型数据的对比关系；图 5b显示了阻尼最小二乘法横波速度结构反演结果与理论模型数据的对比关系。其中，阻尼最小二乘法的迭代次数为9次。

从结果可以看出，阻尼最小二乘法在给定层厚度情况下，可以有效拟合层状介质瑞利面波频散曲线(图 5a)，准确反演浅层横波速度结构(图 5b)。

4 实例分析

本文以某油田工区一条测线的多波多分量实际资料为试验数据，如图 6a所示，为该地震记录中的第23炮数据，道间距为5 m，记录道数为640道，采样间隔2 ms。由图可见，图 6a存在能量较强的瑞利面波，为提取瑞利面波的频散信息、反演浅层横波速度结构提供了必要的前提条件，图 6b为对应的频散曲线信息，瑞利波频散具有多阶模式，基阶能量最强，主要集中在0~3.5 Hz频率范围，高阶能量相对较弱，主要集中在2.5~6.5 Hz，整体噪声干扰较小，仅在甚低频的低速区出现。

在实际操作中，求取大道距采样记录的静校正量具体步骤是：首先，对野外的每一炮记录进行道内插值，消除空间假频；然后，对每一个单炮记录利用τ-p变换方法提取出瑞利面波的频散曲线，基于相应的低速带调查资料获取的层厚度，利用阻尼最小二乘法反演瑞利面波频散曲线，得到每一炮的浅层横波速度结构，并且记录相应速度结构处的CDP点位，由样条插值方法对获取的浅层速度结构进行插值，得到实际资料每个CDP点的横波速度结构，最后给定静校正基准面以及横波替换速度，计算静校正量。由于实例数据道间距较小，本文实际计算中省略第一步道间插值处理。

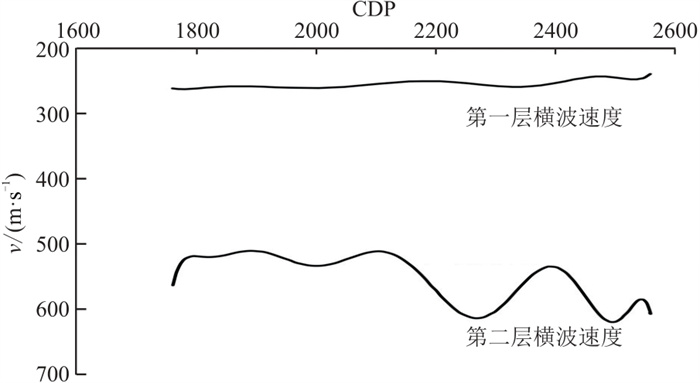
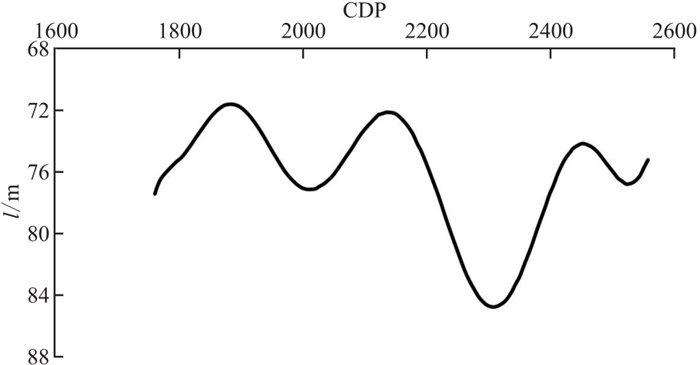
最终的横波速度结构以及第一层界面深度曲线如图 7和图 8所示。由图 7可见：该地区第一层横波速度较稳定，速度在250 m/s左右波动，说明地层的物性结构较均匀；第二层横波速度变化较大，约为500~630 m/s，说明物性结构存在一定差异。图 8由已知资料或采集的折射波资料获取，界面起伏不大，整体变化在72~85 m之间。

最后根据反演结果计算静校正量，并对地震数据做静校正处理。

5 结论

针对大道距采样情况下P-SV静校正问题，本文提出了首先对大道距采样的陆上P-SV地震资料进行小波变换插值，提高地震记录中瑞利波频散信息的可靠性，从而提高利用频散曲线反演浅层横波速度结构的精度，以提高P-SV静校正量的计算精度。通过理论和实际数据的对比应用，验证了该方法的有效性。

(1) 利用小波变换良好的时频分析特性，可以有效地实现基于小波基的地震道内插值，并且具有插值后不会出现空间假频及背景噪声等现象、同相轴的连续性保持较好等优点；

(2) 大道距采样记录经小波变换道内插值后，能够提高瑞利面波频散曲线质量，提取的基阶频散曲线能量更强，拐点更清晰，对低速区域的噪声干扰也有明显压制；

(3) 线性拉东变换法可以快速有效地提取瑞利面波频散曲线，在给定层厚度的情况下，阻尼最小二乘法可有效反演浅层横波速度结构，经过对实际资料的处理表明，该方法具有较好的实用性和可靠性。