构造解释是整个地震资料解释工作的重点和基础,层位追踪和基于层位追踪的地质建模是其重要环节。为了提升层位追踪效率,研究人员提出了很多自动与半自动算法,如相关算法[1-3]、动态时间规整算法[4-5]、地震属性类算法[6-8]等。这些算法能够在横向连续性好、品质较高的资料上高效替代人工解释,但在断层等反射同向轴不连续性较强区域的应用仍有一定限制。
以卷积神经网络为代表的有监督深度学习算法在多种地震资料解释场景中取得了很好的效果,如断层识别[9-11]、盐丘检测[12-13]、沉积相识别[14-16]等。除了上述场景,有监督深度学习算法也可应用于层位追踪。Yang等[17]通过深度卷积网络对较小时窗内的地震数据进行分类,判断时窗中心点是否在同相轴上,从而进行层位追踪。Geng等[18]使用编码—解码U型网络预测相对地质时间体,并从中提取等值面进行层位自动追踪。李海山等[19]在其基础上添加了注意力机制并取得了更好的效果。Tschannen等[20]使用U型网络预测地震数据各点的层位概率密度,将最大概率类别视作分类结果,从而实现层位追踪。Wu等[21]使用U型网络将地震道视为一维图像进行分割,通过提取分割边界获取层位追踪结果。Shi等[22]使用自编码器进行波形嵌入,通过嵌入向量距离获取层位概率并由此追踪层位曲面。尽管有监督深度学习层位追踪方法陆续被提出,但由于人工层位追踪解释结果获取较为困难,由少量标签数据训练的模型泛化能力有限,远离标签数据区域的层位追踪效果较差。
以自编码器为代表的无监督深度学习算法能够从大量无标签数据中提取有效特征,从而实现对数据的降维、去噪等功能[23]。在地震资料解释中,无监督算法学习到的特征可用于地震相分类等任务[24]。然而,无监督学习的结果完全来自数据自身,在缺乏足够先验信息的情况下学习到的数据特征可能是无意义的,无法直接提供分类信息。
半监督学习融合了有监督学习和无监督学习的优势,通过少量标签数据和大量无标签数据训练模型,既能充分利用标签提供的先验信息,又能利用大量无标签数据的内在特征,在解决垃圾邮件识别、目标检测等标签数据获取困难占比较少的场景得到了广泛应用[25]。半监督学习同样适用于层位追踪问题,Di等[26]通过对无标签数据进行无监督学习以约束卷积神经网络有监督学习过程,提升了模型在未被训练区域的预测效果。Wang等[27]将半监督学习和虚拟对抗训练引入层位追踪从而提升了复杂构造区域层位追踪效果。
基于以上分析,本文提出了一种基于卷积神经网络的半监督层位追踪方法,将层位追踪转化为层位间的图像分割。首先使用自编码器对无标签数据进行训练;之后将部分参数迁移至用于分类的卷积神经网络并冻结,从而固定有监督学习过程模型提取的特征;最后使用少量标签数据进行训练,训练完成后对所有剖面进行图像分割,提取分割边缘获取层位追踪结果。
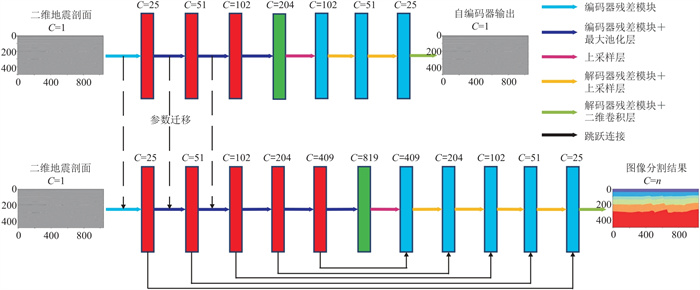
1 方法原理本文所用的网络如图 1所示,包括自编码器和U型网络。
|
图 1 半监督层位追踪网络结构 上图为自编码器,下图为U型网络。C为通道数,n为图像分割类别数。 |
自编码器(图 1上)由编码器残差模块、最大池化层、解码器残差模块、上采样层和二维卷积层构成。当输入工区所有二维地震数据时,编码器部分通过四个残差模块和三次最大池化将单通道地震数据转化为204通道的特征图,解码器部分则通过四个残差模块、三次双线性插值上采样和一个二维卷积层将其恢复为与输入数据相同尺寸的单通道输出。将自编码器输出与输入的地震数据进行损失函数计算,使用Adam优化器更新模型内各参数,重复上述过程直至损失函数收敛[28],此时便可将编码器部分残差模块参数迁移至具有相似结构的U型网络(图 1下)中。
U型网络相较于自编码器增加了最大池化和上采样的次数,同时使用跳跃连接将编码器部分的特征图送入解码器部分对应位置,在通道方向上组合并送入残差模块。根据标签制作时划分的区域总数设置二维卷积层的输出通道数,当工区所有二维地震数据送入U型网络后最终将获得一组与输入数据相同尺寸的多通道输出,将模型输出同标签数据集中由人工解释结果获取的图像分割标签在未被掩码遮挡的区域进行损失函数计算,使用Adam优化器更新模型内参数,重复上述过程直至损失函数收敛。当标签数据有监督训练完成后,使用U型网络对整个工区的地震数据进行预测,提取各点最大概率类别以获取图像分割结果,提取图像分割边界作为层位追踪结果。
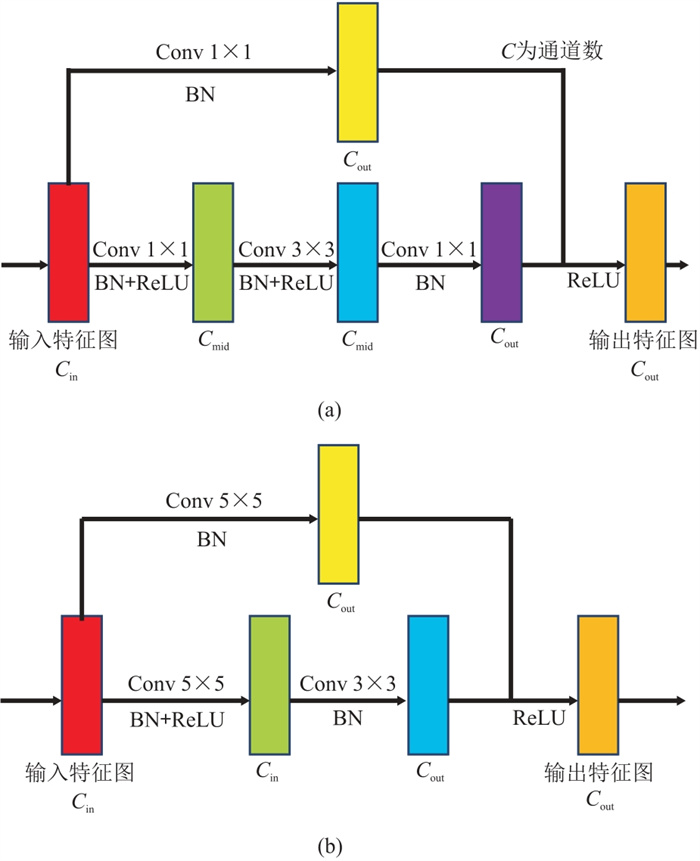
残差模块来源于ResNet框架,通过在连续卷积层间添加短连接可以抑制模型层数增加导致的模型退化现象,同时也可以借助这些短连接使得不同尺度的特征作为同一层的输入丰富模型层次从而提升模型性能[29-30]。图 1中自编码器与U型网络中替换的编码器残差模块与解码器残差模块如图 2所示。其中,图 2a为编码器残差模块,由三个卷积层构成的主线和一个卷积层构成的支线组成,主线卷积核尺寸分别为1×1、3×3、1×1,支线卷积核尺寸为1×1,二者输出的张量对应相加后由ReLU函数激活得到残差模块输出。图 2b为解码器残差模块,由两个卷积层构成的主线和一个卷积层构成的支线组成,主线卷积核尺寸分别为5×5、3×3,支线卷积核尺寸为5×5,二者输出的张量对应相加后由ReLU函数激活得到输出。
|
图 2 残差模块结构
(a)编码器残差模块;(b)解码器残差模块 Cin为输入特征图通道数;Cmid为编码器残差模块中间特征图通道数;Cout为输出通道数;Conv为二维卷积层;BN(Batch Normalization)为批归一化层;ReLU为非线性激活函数。 |
本文模型使用最大池化层实现编码器的下采样操作,每次下采样均会使特征图在各个维度的尺寸减半,不但可以减少算力需求,还可以在一定程度上增强模型的泛化能力。上采样则使用双线性插值函数恢复尺寸,因此该模型对于输入数据尺寸没有要求,可以将不同方向的剖面混合训练从而提升训练效果。相较于U型网络,自编码器下采样次数只有三次,一方面是为了增加无标签数据训练效率,更重要的是过多的下采样会使得后续参数迁移时带去过多的大尺度特征,从而影响标签数据有监督学习的收敛速度。相较于其他迁移学习中不冻结参数并以较低学习率微调的做法,本文通过冻结迁移的参数使得有监督学习过程使用的初始特征完全来自于自编码器的训练,这些特征来自于该工区所有的地震剖面,不随标签数据的有监督学习而改变,对于增强远离标签剖面的无标签数据的层位追踪效果具有重要意义。
自编码器的训练是一回归问题,本文基于均方误差(Mean Square Error, MSE)和多尺度结构相似性(Multi-Scale Structural Similarity Index, MS-SSIM)构建了一种混合损失函数
| $ L=\alpha {L}_{\mathrm{M}\mathrm{S}\mathrm{E}}+\beta {L}_{\mathrm{M}\mathrm{S}-\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}} $ | (1) |
式中:
| $ {L}_{\mathrm{M}\mathrm{S}\mathrm{E}}=\frac{1}{N}\sum\limits_{i=1}^{N}({y}_{i}-{x}_{i}{)}^{2} $ | (2) |
式中:
| $ \begin{array}{l}{L}_{\mathrm{M}\mathrm{S}-\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}}=1-{\left(\frac{2{\mu }_{{x}_{S}}{\mu }_{{y}_{S}}+{C}_{1}}{{\mu }_{{x}_{S}}^{2}+{\mu }_{{y}_{S}}^{2}+{C}_{1}}\right)}^{{w}_{S}}\times \\ \prod\limits_{i=1}^{S}{\left(\frac{2{\sigma }_{{x}_{i}{y}_{i}}+{C}_{2}}{{\sigma }_{{x}_{i}}^{2}+{\sigma }_{{y}_{i}}^{2}+{C}_{2}}\right)}^{{w}_{i}}\end{array} $ | (3) |
式中:
U型网络的训练是一分类问题,本文选用交叉熵函数计算损失
| $ {L}_{\mathrm{C}\mathrm{E}}=-\frac{1}{N}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{n}p\left({x}_{ij}\right)\mathrm{l}\mathrm{n}q\left({x}_{ij}\right) $ | (4) |
式中:
为了能更好地对比本文提出的半监督层位追踪方法与相同模型下有监督层位追踪方法的层位追踪效果,本文在定性评价的基础上选择了多个参数进行定量评价,包括图像分割平均交并比(Mean Intersection over Union,MIoU)、图像分割边界平均交并比、边界精确度与待追踪层位的采样点预测误差。平均交并比来源于混淆矩阵,是多个类别交并比的平均数,常被用于图像分割问题的定量评价。相较于其他图像分割问题,层位追踪更关注地震数据图像分割结果边界的准确性,因此本文还使用了图像分割边界平均交并比,将地震数据图像分割结果边界进行提取并计算平均交并比。对于层位追踪问题,相较于所有正样本被预测出的样本总数,更重要的是预测结果的可靠性,而精确度(Precision)是预测为真的样本中实际标签为真的比例,因此本文计算了多个层位的精确度并求取均值对预测结果的可靠性进行定量评价。除此之外,为了更直观地评价层位追踪效果,本文分别计算多个层位的预测误差,通过误差的采样点数大小对比有监督方法和半监督方法层位追踪结果。
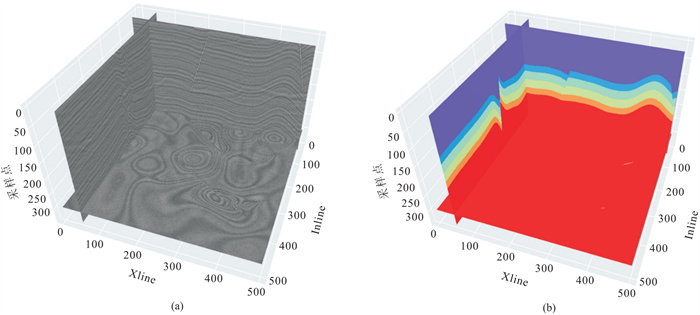
2 合成数据测试本文首先在合成数据上进行基于卷积神经网络的半监督层位追踪方法的测试。本文改进了Wu等[32]提出的方法以实现模拟数据的合成。首先建立水平层状模型,之后通过类高斯位移场和椭圆位移场依次实现了褶皱和断层的模拟,通过曲面插值将数据归整到网格点上,最后选取子波褶积并添加随机噪声获得合成数据体。该数据体尺寸为501 Inline×501 Xline×338采样点,从中挑选了5个待追踪层位(从浅到深为层位1~层位5)和错断这些层位的断层一起将合成数据体划分为6个图像分割类别,合成数据体与标签数据体如图 3所示。
|
图 3 合成数据标签制作 (a)合成数据体;(b)标签数据体 |
在使用上述方法进行测试前需进行数据预处理,包括地震数据的标准化、地震数据分割标签制作和样本数据增强。本文中对地震数据进行标准化
| $ {A}_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}}=\frac{A-{A}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}}{{A}_{\mathrm{d}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}} $ | (5) |
式中:
|
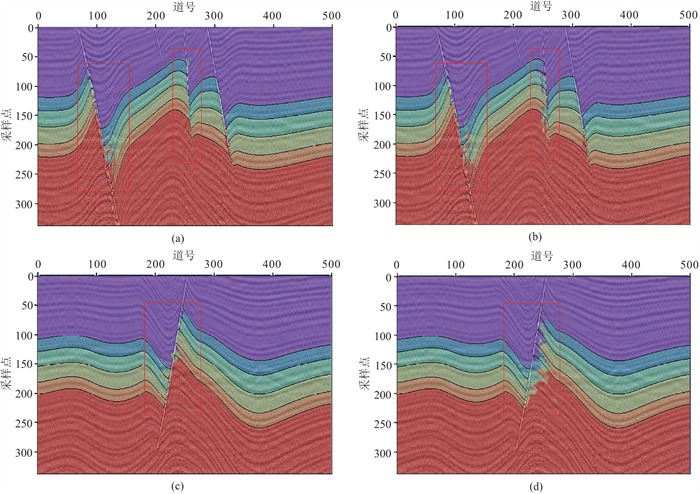
图 4 两种方法在合成数据上的剖面效果展示 (a)Inline250半监督结果;(b)Inline250有监督结果;(c)Xline250半监督结果;(d)Xline250有监督结果 |
在四张TeslaV100S平台上使用U型网络进行40轮的有监督训练,并使用自编码器和U型网络进行100轮的无监督训练参数迁移后进行40轮的有监督训练,前者耗时35 min,后者耗时63 min。两种方法在合成数据的部分分割结果如图 4所示。由图可见,在地层平缓的区域两种方法的地震数据分割边界与实际层位匹配程度都较高;但在红框标注的断层附近区域,相较于有监督方法,半监督方法的地震数据图像分割结果效果更好,错误分割更少,边界也更接近实际层位。
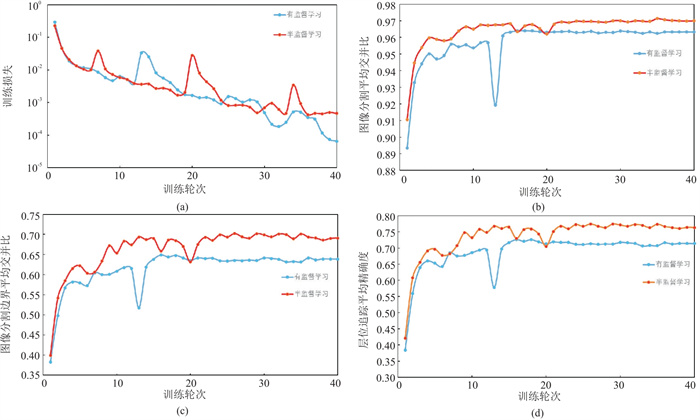
图 5为训练过程中两种方法训练损失、MIoU和精确度的变化曲线。由图可见,两种方法预测结果的图像分割MIoU差异小于0.05,半监督方法略高一些;而对于图像分割边界MIoU和精确度两个参数半监督方法结果明显优于有监督流程结果。
|
图 5 两种方法学习过程的参数变化 (a)训练损失;(b)图像分割平均交并比;(c)层位追踪平均交并比;(d)层位追踪平均精确度 |
表 1为两种方法训练完成后模型最终预测结果的定量参数评价。由表 1可见,半监督方法结果在图像分割边界MIoU、精确度和层位预测误差方面均优于有监督方法结果,其中误差差值最大的是层位1,最小的是层位2,分别为0.2335个采样间隔和0.0037个采样间隔。
|
|
表 1 合成数据层位追踪评价参数 |
为了对比两种方法在远离标签剖面的泛化能力,本文计算了位于8个标签剖面正中间的6个剖面的评价参数(表 2)。相较于表 1,表 2的各参数都有所劣化,这验证了关于地震数据渐变性对预测效果影响的假设。同表 1类似,表 2中半监督方法结果的层位预测误差均小于有监督方法结果,其中层位5误差差值最大,层位4误差差值最小,分别为0.5481个采样间隔和0.1965个采样间隔。
|
|
表 2 标签中央剖面层位追踪评价参数 |
合成数据测试结果的分析表明,两种方法在地层平缓的区域具有相近的分割结果,但在断层附近区域半监督方法结果具有较少的错误分割,分割边界更接近目的层位的真实位置,层位误差较小,具有更好的层位追踪效果。在远离标签剖面区域,两种方法的层位预测误差差异更加明显,本文的半监督方法具有更强的泛化能力。
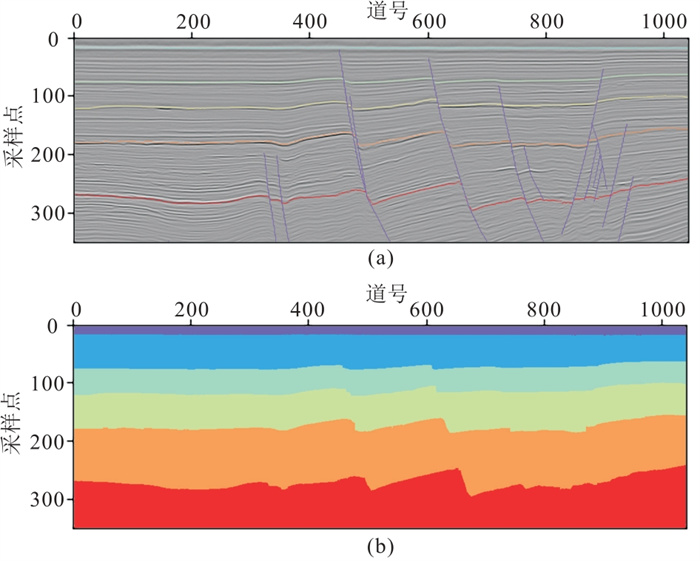
3 实际应用为了测试上述方法在实际数据的应用效果,选取新西兰塔拉纳基盆地数据体。该数据体尺寸为396 Inline×1043 Xline×352采样点,采样间隔为2 ms,其中包含了断层和5个层位(从浅到深为层位1~层位5)的解释结果,地震数据图像分割标签共包含六类,如图 6所示。解释结果只对部分剖面进行了断层和层位的人工解释,包括Inline剖面46、196、346和Xline剖面142、342、542、742、942,有监督学习过程使用的标签由人工解释结果得来,标签区域约占工区整体的2%,其余部分由掩码代替。
|
图 6 实际数据标签制作 (a)层位与断层人工解释结果;(b)图像分割标签 |
在相同平台上使用U型网络进行40轮的有监督训练,并使用自编码器和U型网络进行100轮的无监督训练参数迁移后进行40轮的有监督训练,前者耗时41 min,后者耗时70 min。部分分割结果如图 7~图 8所示。两个剖面临近标签剖面中央,与标签剖面差异较大,可以很好的对比两种方法的泛化能力。
|
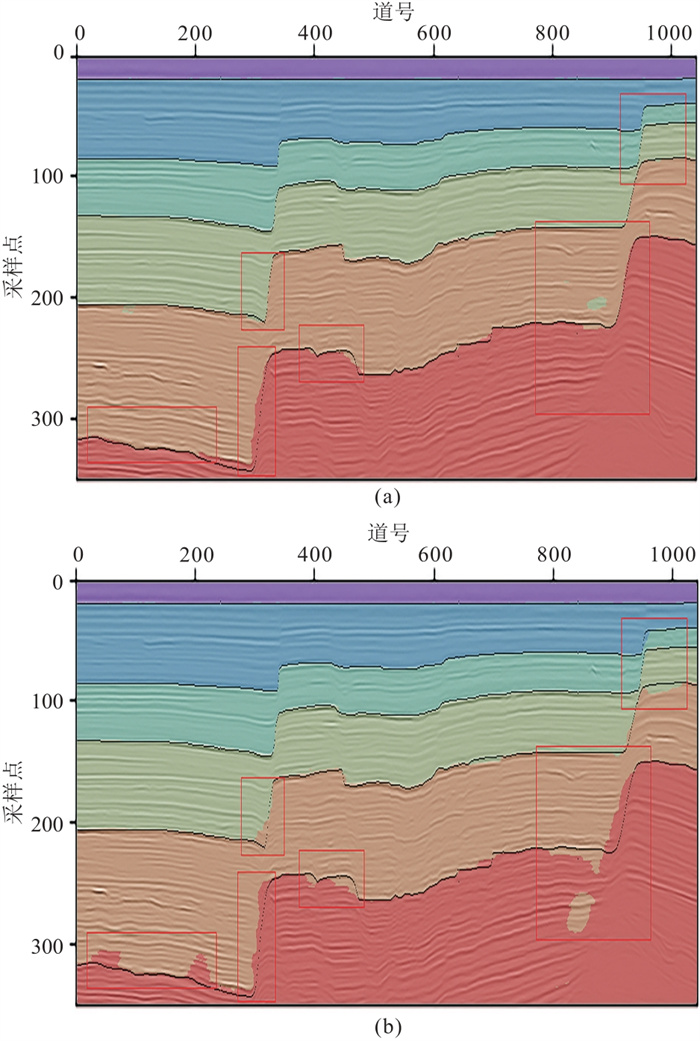
图 7 两种方法在Inline271的剖面效果展示 (a)半监督层位追踪结果;(b)有监督层位追踪结果 |
|
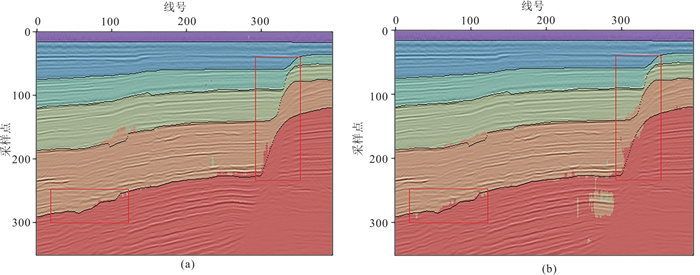
图 8 两种方法在Xline842的剖面效果展示 (a)半监督层位追踪结果;(b)有监督层位追踪结果 |
由图 7可见,相较于有监督方法结果,半监督方法结果在Inline271剖面中两个正断层的两盘均有较好的分割效果,分割边界更接近人工解释结果,错误分割较少,在层位较深的区域两种方法的结果差异也越大。由图 8可见,两种方法的结果在Xline842剖面中浅层和地层平缓区域的地震数据分割边界与实际层位吻合较好;在较深区域和断层两盘的分割边界与实际层位均存在一定误差,但半监督方法结果具有较少的错误分割和较高的边界吻合度。
在标签中央剖面的分割结果进行定性评价的基础上,本文也对多个定量评价参数进行了计算(表 3)。由表 3可见,两种方法的图像分割MIoU均大于0.95,且差异很小,但边界MIoU与精确度均有较大差异,这表明两种方法在标签中央剖面的分割结果与地震数据分割标签十分相似,但半监督方法分割结果的边界更接近人工层位解释结果,这与标签中央剖面的定性评价一致。半监督方法结果的层位预测误差均小于有监督方法结果,深层的层位4和层位5的预测误差较大,浅层的层位1至层位3预测误差较小,误差差值最大的为层位5和层位4,与定性评价结果一致。
|
|
表 3 标签中心剖面层位追踪评价参数 |
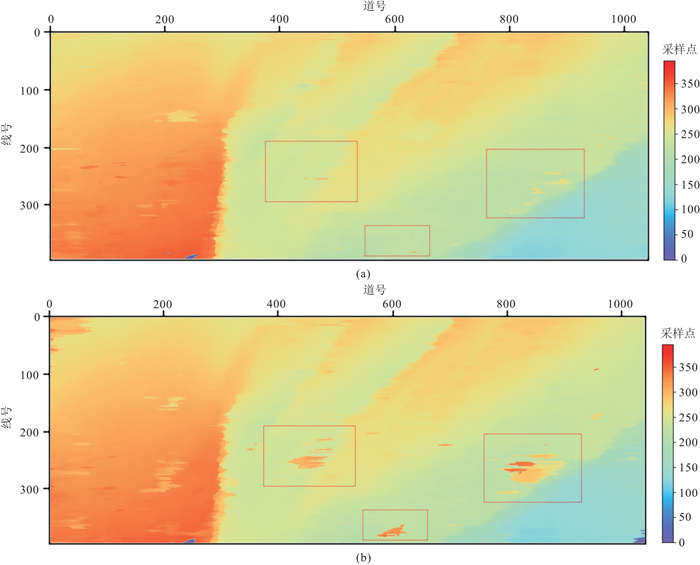
图 9为两种方法的层位5追踪结果,颜色代表采样点深度。由图可见,相较于有监督方法结果,半监督方法结果在红框区域具有较少的突变,即具有较少的错误分割,这些突变区域大多位于标签中央剖面附近,与附近的标签剖面差异较大,这说明半监督方法有效提升了模型在远离标签剖面区域的泛化能力。
|
图 9 两种方法追踪结果的层位5平面图 (a)半监督层位追踪结果;(b)有监督层位追踪结果 |
实际数据测试结果表明,本文的半监督方法与有监督方法在地层平缓区域和浅层的层位具有相近的分割结果和边界,但在深层和断层附近区域半监督方法结果具有较少的错误分割,边界更接近人工解释结果。在远离标签剖面的区域层位追踪结果具有较少突变,泛化能力优于有监督方法。
4 结论针对少量人工标签训练导致有监督层位追踪泛化能力较差的问题,本文在有监督层位追踪方法基础上添加自编码器的无监督学习,对工区全部二维剖面进行训练,通过参数迁移和冻结使得有监督学习过程的初始特征完全来自于自编码器的训练,之后进行掩码标签的有监督学习,从而实现基于卷积神经网络的半监督层位追踪。
合成数据和实际数据的应用结果均表明,在层位较为平缓的区域,两种方法均具有相近的分割结果;但在断层和深层区域,半监督方法具有较少的错误分割,分割边界更接近人工层位解释结果。在远离标签剖面区域,合成数据测试结果表明两种方法的层位预测误差的差异相较工区整体的层位预测误差增大,实际数据应用结果表明半监督方法结果具有较少的突变。因此,相较于有监督方法,本文提出的半监督方法具有更好的泛化能力,具有一定的应用前景。
| [1] |
MARFURT K J, KIRLIN R L, FARMER S L, et al. 3-D seismic attributes using a semblance-based coherency algorithm[J]. Geophysics, 1998, 63(4): 1150-1165. |
| [2] |
GERSZTENKORN A, MARFURT K J. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. |
| [3] |
GALIANA-MERINO J J, ROSA-HERRANZ J L, ROSA-CINTAS S, et al. Seismic wave tool: continuous and discrete wavelet analysis and filtering for multichannel seismic data[J]. Computer Physics Communications, 2013, 184(1): 162-171. |
| [4] |
WU X M, FOMEL S. Least-squares horizons with local slopes and multigrid correlations[J]. Geophysics, 2018, 83(4): IM29-IM40. |
| [5] |
JIN S, CHEN S Q, WEI J X, et al. Automatic seismic event tracking using a dynamic time warping algorithm[J]. Journal of Geophysics and Engineering, 2017, 14(5): 1138-1149. |
| [6] |
FORTE E, DOSSI M, PIPAN M, et al. Automated phase attribute-based picking applied to reflection seismics[J]. Geophysics, 2016, 81(2): V55-V64. |
| [7] |
BORGOS H G, SKOV T, SØNNELAND L. Automated Structural Interpretation through Classification of Seismic Horizons[M]. Springer Berlin Heidelberg, 2005: 89-106.
|
| [8] |
李鹏, 冯晅, 王典, 等. 地震剖面同相轴自动追踪技术研究[J]. 吉林大学学报(地球科学版), 2008, 38(增刊1): 76-79. LI Peng, FENG Xuan, WANG Dian, et al. Auto tracking the syncphase axis of seismic profiles[J]. Journal of Jilin University(Earth Science Edition), 2008, 38(S1): 76-79. |
| [9] |
HUANG L, DONG X, CLEE T E. A scalable deep learning platform for identifying geologic features from seismic attributes[J]. The Leading Edge, 2017, 36(3): 249-256. |
| [10] |
WU X, LIANG L, SHI Y, et al. FaultSeg3D: using synthetic datasets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45. |
| [11] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [12] |
WALDELAND A U, JENSEN A C, GELIUS L J, et al. Convolutional neural networks for automated seismic interpretation[J]. The Leading Edge, 2018, 37(7): 529-537. |
| [13] |
张玉玺, 刘洋, 张浩然, 等. 基于深度学习的多属性盐丘自动识别方法[J]. 石油地球物理勘探, 2020, 55(3): 475-483. ZHANG Yuxi, LIU Yang, ZHANG Haoran, et al. Multi-attribute automatic interpretation of salt domes based on deep learning[J]. Oil Geophysical Prospecting, 2020, 55(3): 475-483. |
| [14] |
PHAM N, FOMEL S, DUNLAP D. Automatic channel detection using deep learning[J]. Interpretation, 2019, 7(3): SE43-SE50. |
| [15] |
陈海洋, 汪玲玲. 基于LinkNet的地震相自动划分[J]. 石油地球物理勘探, 2023, 58(3): 518-527. CHEN Haiyang, WANG Lingling. Automatic seismic facies classification based on LinkNet[J]. Oil Geophysical Prospecting, 2023, 58(3): 518-527. |
| [16] |
杨存, 孟贺, 叶月明, 等. 沉积相智能地震识别技术研究及应用[J]. 石油地球物理勘探, 2023, 58(3): 528-539. YANG Cun, MENG He, YE Yueming, et al. Research and application of intelligent seismic identification technology of sedimentary facies[J]. Oil Geophysical Prospecting, 2023, 58(3): 528-539. |
| [17] |
YANG L, SUN S Z. Seismic horizon tracking using a deep convolutional neural network[J]. Journal of Petroleum Science and Engineering, 2020, 187: 106709. |
| [18] |
GENG Z, WU X, SHI Y, et al. Deep learning for relative geologic time and seismic horizons[J]. Geophysics, 2020, 85(4): WA87-WA100. |
| [19] |
李海山, 杨午阳, 伍新明, 等. 基于深度学习的相对地质时间体估计方法[J]. 石油地球物理勘探, 2023, 58(2): 277-284. LI Haishan, YANG Wuyang, WU Xinming, et al. Relative geological time volume estimation method based on deep learning[J]. Oil Geophysical Prospecting, 2023, 58(2): 277-284. |
| [20] |
TSCHANNEN V, DELESCLUSE M, ETTRICH N, et al. Extracting horizon surfaces from 3D seismic data using deep learning[J]. Geophysics, 2020, 85(3): N17-N26. |
| [21] |
WU H, ZHANG B, LIN T, et al. Semi-automated seismic horizon interpretation using the encoder-decoder convolutional neural network[J]. Geophysics, 2019, 84(6): B403-B417. |
| [22] |
SHI Y, WU X, FOMEL S. Waveform embedding: automatic horizon picking with unsupervised deep learning[J]. Geophysics, 2020, 85(4): WA67-WA76. |
| [23] |
VINCENT P, LAROCHELLE H, BENGIO Y, et al. Extracting and composing robust features with denoising autoencoders[C]. Proceedings of the 25th International Conference on Machine Learning, 2008, 1096-1103.
|
| [24] |
王倩楠, 王治国, 杨阳, 等. 基于多特征融合自编码器的无监督地震相分类研究[J]. 地球物理学报, 2024, 67(1): 370-378. WANG Qiannan, WANG Zhiguo, YANG Yang, et al. Unsupervised seismic facies classificatio based on multi-feature fusion autoencoder[J]. Chinese Journal of Geophysics, 2024, 67(1): 370-378. |
| [25] |
周志华. 基于分歧的半监督学习[J]. 自动化学报, 2013, 39(11): 1871-1878. ZHOU Zhihua. Disagreement-based semi-supervised learning[J]. Acta Automatica Sinica, 2013, 39(11): 1871-1878. |
| [26] |
DI H, LI Z, MANIAR H, et al. Seismic stratigraphy interpretation by deep convolutional neural networks: a semisupervised workflow[J]. Geophysics, 2020, 85(4): WA77-WA86. |
| [27] |
WANG F, WU X, WANG H. Seismic horizon identification using semi-supervised learning with virtual adversarial training[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-11. |
| [28] |
贾文娟, 张煜东. 自编码器理论与方法综述[J]. 计算机系统应用, 2018, 27(5): 1-9. JIA Wenjuan, ZHANG Yudong. Survey on theories and methods of autoencoder[J]. Computer System & Applications, 2018, 27(5): 1-9. |
| [29] |
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, 2016, 770-778.
|
| [30] |
VEIT A, WILBER M, BELONGIE S. Residual networks are exponential ensembles of relatively shallow networks[DB/OL]. (2016-05-20)[2024-03-10]. https://arxiv.org/abs/1605.06431.
|
| [31] |
WANG Z, SIMONCELLI E P, BOVIK A C. Multiscale structural similarity for image quality assess-ment[C]. The Thirty-seventh Asilomar Conference on Signal, Systems & Computers, 2003, 2: 1398-1402.
|
| [32] |
WU X, GENG Z, SHI Y, et al. Building realistic structure models to train convolutional neural networks for seismic structural interpretation[J]. Geophysics, 2020, 85(4): WA27-WA39. |



 李沐阳, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院,730020。Email:
李沐阳, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院,730020。Email: 