2. 油气资源与勘探技术教育部重点实验室(长江大学), 湖北武汉 430100;
3. 中国地质大学(武汉)地球物理与空间信息学院, 湖北武汉 430074
2. Key Laboratory of Exploration Technologies for Oil and Gas Resources, Ministry of Education, Yangtze University, Wuhan, Hubei 430100, China;
3. School of Geophysics and Geomatics, China University of Geosciences (Wuhan), Wuhan, Hubei 430074, China
瞬变电磁法(TEM)是一种时间域人工源电磁法,广泛应用于矿产资源勘探。该方法利用不接地回线源或接地线源向地下发射一次脉冲磁场,通过观测地下介质感应产生的二次场分析地层的电性特征[1]。与频域方法相比,瞬变电磁法理论上具有受低阻层影响小、体积效应小、分辨率高、旁侧影响小及测量快速、高效等优点[2-3]。地—井瞬变电磁法是近年来发展较快、地质找矿效果较好的一种电法勘探方法,主要应用于金属矿的勘查、构造填图及油气田、煤田、地下水、地热、冻土带、海洋地质等领域的研究[4]。在金属矿勘查方面,该方法主要应用于井旁、井底盲矿体的勘察,尤其目标矿体深度太大、受电性干扰因素(如导电覆盖层、浅部硫化物、地表矿化地层等)影响的地区,应用地面电磁法进行勘探更能体现其优越性[5]。在加拿大、澳大利亚等国家,地—井TEM法已成为常规勘查方法,有很多成功的深部找矿实例。1995年利用地—井TEM法在加拿大Falconbridge Lindsley铜镍矿区发现深1280 m、厚28 m的富矿[6-7]。野外数据采集时,将发射回线装置布置在钻孔上方或附近地面,向地下发送双极性脉冲,将探头沿钻孔或井眼逐点下沉,测量地质体感应产生的瞬变电磁响应[8]。该方法具有受地面电磁场或人文干扰小、电磁信号强等优势,在深部找矿、地质构造研究等方面得到了广泛应用,尤其对金属矿的开发具有不可替代的作用。
早期的钻井一般都是竖直井,瞬变电磁法测井仪器只能进行单一方向的测量,因而无法研究地层电性各向异性的影响。随着科技的进步,开始钻探水平井和大斜度井。由于地层电性各向异性会影响测量结果的精确性,给各向异性储层的解释和评价带来困难[9]。O’Brien等[10]推导了层状各向异性介质中电磁场的递推公式;Weiss等[11]通过数值模拟研究了电性源在各向异性介质中产生的电磁场分布特征;Pek等[12]较全面和完善地阐述了一维各向异性地层的正演问题。之后,地球物理学家们对地层各向异性及矢量电磁场的研究取得了初步进展[13-14],多分量和方向感应测井技术相继出现,其方法也逐步成熟[15]。徐世浙等[16]采用有限元法计算了二维电性各向异性地电断面的大地电磁场;Yu等[17]分析了三维各向异性海底对TEM响应的影响;王昌学等[18]使用交错网格有限差分法模拟了电性各向异性地层的频率域电磁响应;孙向阳等[19]采用矢量有限元法研究了倾斜各向异性地层中随钻测井电磁响应的分布特征;陈桂波等[20]使用积分方程法模拟研究了三维电性异常体在各向异性地层中的电磁响应;Dennis等[21]研究了电各向异性介质在近地表的瞬变电磁响应特征;严良俊等[22]研究了一维油气储层电各向异性对瞬变电磁响应中视电阻率的影响;王煜翔[23]实现了电性源瞬变电磁法一维各向异性模型的正、反演;周建美等[24]和刘亚军等[25]采用有限体积法研究了不同方向的电导率各向异性对电磁场分量的影响;刘亚军[26]采用有限体积法实现了回线源和长偏移距瞬变电磁法的三维各向异性介质的正演;郭建磊等[27-28] 采用有限差分法研究了轴向各向异性地—井和巷—孔瞬变电磁响应随深度变化的特征。关于瞬变电磁法在各向异性介质地—井测井中时间域的研究鲜有报道。基于地—井瞬变电磁法在各向异性介质中的响应规律的初步研究[29],本文在时间域各向异性介质响应的基础上,采用具有灵活性和适应性、能够较好地贴合地形变化、多适用于复杂地质模型计算的有限元数值模拟方法,针对地—井瞬变电磁方位测井中发射源沿井孔不同方向布置的情况,研究并分析了时间域瞬变电磁响应特征。本文研究结果能对地—井瞬变电磁法的各向异性解释提供指导,也为地—井瞬变电磁勘探的多方位测井和各向异性反演提供参考。
1 各向异性介质电磁场正演基本理论 1.1 各向异性介质的时间域电磁法控制方程由麦克斯韦方程组得到电场强度矢量所满足的时间域波动方程[30]
| $ \nabla \times \nabla \times \boldsymbol{E}+\mu \boldsymbol{\sigma }\frac{\partial \boldsymbol{E}}{\partial t}+\mu \frac{\partial \boldsymbol{J}}{\partial t}=0 $ | (1) |
式中:μ为磁导率;J为发射源的电流密度;σ为各向异性电导率张量;E为待求电场;t为时间。在不同电性介质分界面,电场强度矢量满足边界条件
| $ \boldsymbol{n}\times \left({\boldsymbol{E}}_{1}-{\boldsymbol{E}}_{2}\right)=0 $ | (2) |
式中:n为界面上的单位法向量;E1、E2分别为边界两侧介质1和介质2内的电场强度矢量。
在各向异性介质中,电阻率ρ和电导率σ可用张量形式表示为[25]
| $ \left\{\begin{array}{l}\boldsymbol{\rho }={\boldsymbol{\sigma }}^{-1}\\ \boldsymbol{\sigma }=\left(\begin{array}{ccc}{\sigma }_{xx}& {\sigma }_{xy}& {\sigma }_{xz}\\ {\sigma }_{yx}& {\sigma }_{yy}& {\sigma }_{yz}\\ {\sigma }_{zx}& {\sigma }_{zy}& {\sigma }_{zz}\end{array}\right)\end{array}\right. $ | (3) |
为了便于计算,任意电导率张量σ可由主轴各向异性电导率张量σ0经三次欧拉旋转得到[31]
| $ {\boldsymbol{\sigma }}_{0}=\left(\begin{array}{ccc}{\sigma }_{x}& 0& 0\\ 0& {\sigma }_{y}& 0\\ 0& 0& {\sigma }_{z}\end{array}\right) $ | (4) |
式中σx、σy和σz分别为主电导率沿x、y、z方向的分量。
在笛卡尔坐标系中,电导率张量可以表示为
| $ \boldsymbol{\sigma }=\boldsymbol{D}{\boldsymbol{\sigma }}_{0}{\boldsymbol{D}}^{-\mathrm{T}} $ | (5) |
式中
| $ {\boldsymbol{D}}_{1}=\left(\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}\alpha & -\mathrm{s}\mathrm{i}\mathrm{n}\alpha & 0\\ \mathrm{s}\mathrm{i}\mathrm{n}\alpha & \mathrm{c}\mathrm{o}\mathrm{s}\alpha & 0\\ 0& 0& 1\end{array}\right) $ | (6) |
| $ {\boldsymbol{D}}_{2}=\left(\begin{array}{ccc}1& 0& 0\\ 0& \mathrm{c}\mathrm{o}\mathrm{s}\beta & -\mathrm{s}\mathrm{i}\mathrm{n}\beta \\ 0& \mathrm{s}\mathrm{i}\mathrm{n}\beta & \mathrm{c}\mathrm{o}\mathrm{s}\beta \end{array}\right) $ | (7) |
| $ {\boldsymbol{D}}_{3}=\left(\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}\gamma & -\mathrm{s}\mathrm{i}\mathrm{n}\gamma & 0\\ \mathrm{s}\mathrm{i}\mathrm{n}\gamma & \mathrm{c}\mathrm{o}\mathrm{s}\gamma & 0\\ 0& 0& 1\end{array}\right) $ | (8) |
其中α、β、γ分别为各向异性走向角、倾角和偏角[32]。
1.2 空间域和时间域离散使用有限单元法离散波动方程式(1),根据Galerkin方法定义残差为[33]
| $ \boldsymbol{R}=\nabla \times \nabla \times \boldsymbol{E}+\mu \boldsymbol{\sigma }\frac{\partial \boldsymbol{E}}{\partial t}+\mu \frac{\partial \boldsymbol{J}}{\partial t} $ | (9) |
非结构四面体网格离散计算区域见图 1,采用自动满足电场切向分量连续且无散的Nédélec矢量插值基函数近似表达单元内电场的线性分布。在单个有限元剖分单元Ve内,任意位置的电场可以表示为
| $ {u}^{e}=\sum\limits_{j=1}^{6}{u}_{j}^{e}\cdot {N}_{j}^{e} $ | (10) |
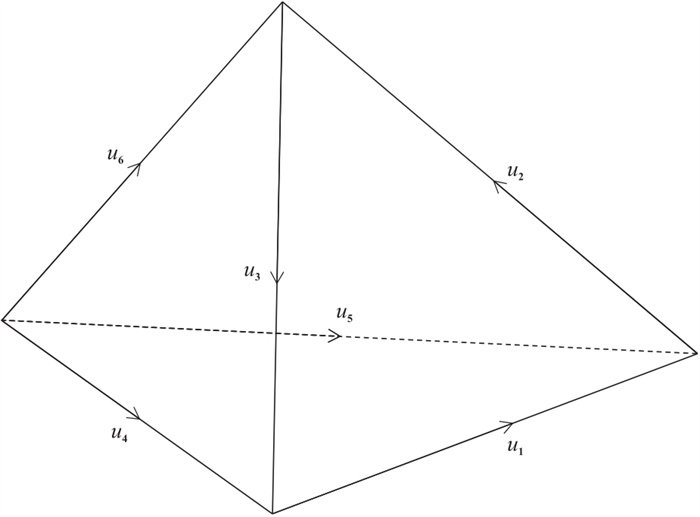
|
图 1 非结构自由四面体网格单元 |
式中:e为单元编号;j为剖分单元内棱边编号;
| $ \boldsymbol{S}\cdot \boldsymbol{E}+\boldsymbol{M}\frac{\partial \boldsymbol{E}}{\partial t}=-\boldsymbol{J} $ | (11) |
式中:S为刚度矩阵;M为质量矩阵。在单元Ve内,有
| $ \boldsymbol{S}=\frac{1}{\mu }\underset{{V}^{e}}{\overset{}{\iiint }}\left(\nabla \times \boldsymbol{N}\right)\cdot \left(\nabla \times \boldsymbol{N}\right)\mathrm{d}V $ | (12) |
| $ \boldsymbol{M}=\underset{{V}^{e}}{\overset{}{\iiint }}\boldsymbol{N}\cdot \boldsymbol{\sigma} \cdot \boldsymbol{N}\mathrm{d}V $ | (13) |
| $ \boldsymbol{J}=\underset{{V}^{e}}{\overset{}{\iiint }}\boldsymbol{N}\cdot \frac{\partial \boldsymbol{J}}{\partial t}\mathrm{d}V $ | (14) |
式中N={ Nj , j=1~6}
在时间域,为提高精度,采用二阶后退欧拉差分格式进行离散[30]
| $ \frac{\partial {\boldsymbol{{E}}}^{\left(i\right)}}{\partial t}=\frac{1}{2\mathrm{\Delta }{t}_{i}}\left[3{\boldsymbol{{E}}}^{\left(i\right)}-4{\boldsymbol{{E}}}^{(i-1)}+{\boldsymbol{{E}}}^{(i-2)}\right] $ | (15) |
式中:i为时间点编号;∆ti为第i时刻前两道的时间步长。将式(11)代入式(15)可得
| $ \left(3\boldsymbol{S}+2\mathrm{\Delta }{t}_{i}\boldsymbol{M}\right){\boldsymbol{E}}^{\left(i\right)}=\boldsymbol{S}\left[4{\boldsymbol{E}}^{\left(i-1\right)}-{\boldsymbol{E}}^{\left(i-2\right)}\right]-2\mathrm{\Delta }{t}_{i}{\boldsymbol{J}}^{\left(i\right)} $ | (16) |
最终形成大型线性方程组
| $ \boldsymbol{K}\cdot \boldsymbol{E}=\boldsymbol{b} $ | (17) |
其具体方程式为
| $ \left(\begin{array}{cccccc}3S+2\mathrm{\Delta }{t}_{1}M& & & & & \\ -4S& 3S+2\mathrm{\Delta }{t}_{2}M& & & & \\ S& -4S& 3S+2\mathrm{\Delta }{t}_{3}M& & & \\ & S& -4S& 3S+2\mathrm{\Delta }{t}_{4}M& & \\ & & \ddots & \ddots & \ddots & \\ & & & S& -4S& 3S+2\mathrm{\Delta }{t}_{n}M\end{array}\right)\left(\begin{array}{c}{E}_{1}\\ {E}_{2}\\ {E}_{3}\\ {E}_{4}\\ ⋮\\ {E}_{n}\end{array}\right)=\left(\begin{array}{c}-2\mathrm{\Delta }{t}_{1}{J}_{1}+3S{E}_{0}\\ -2\mathrm{\Delta }{t}_{2}{J}_{2}-S{E}_{0}\\ -2\mathrm{\Delta }{t}_{3}{J}_{3}\\ -2\mathrm{\Delta }{t}_{4}{J}_{4}\\ ⋮\\ -2\mathrm{\Delta }{t}_{n}{J}_{n}\end{array}\right) $ | (18) |
式中:n为时间点数;S、M、E、J分别表示矩阵S、M、E、J对应位置的元素,与列向量E在离散模型中所在棱边一一对应。
对于接地长导线发射源,常采用方波、三角波、正弦波、梯形波等初始电流为零的电性源,其初始电场
| $ {\boldsymbol{E}}^{\left(0\right)}={\boldsymbol{{E}}}_{\mathrm{S}}^{\left(0\right)}+{\boldsymbol{E}}_{\mathrm{D}\mathrm{C}}^{\left(0\right)} $ | (19) |
式中:
| $ {\boldsymbol{E}}_{\mathrm{D}\mathrm{C}}^{\left(0\right)}=-\nabla φ $ | (20) |
对直流电场及时域电磁场问题同样采用四面体网格,以保证直流电场与矢量电场边界的一致性,且直流场问题与时域电磁问题均采用总场方法求解。由于求解区域较大,在计算过程中对外边界Г均施加Dirichlet边界条件[30]
| $ \left\{\begin{array}{l}\boldsymbol{\varPhi }{|}_{\varGamma }=0\\ \left(\boldsymbol{n}\times \boldsymbol{e}\right){|}_{\varGamma }=0\end{array}\right. $ | (21) |
式中:
对于求解形如式(17)的大型稀疏矩阵,Intel Math Kernel Library (MKL)函数库的PARDISO求解器具有节约系统存储空间、计算和并行效率高及随节点数的增加具有接近线性加速比等优点[35]。使用Compressed Sparse Row (CSR)存储格式,将式(18)左端的稀疏矩阵分配并压缩存储为3个一维矩阵,分别存储稀疏矩阵的非零元素、每个非零元素所在列数和每个非零元素前的零元素个数。通过PARDISO求解器,选择合适参数对矩阵进行LU分解、快速迭代求解,得到所有四面体的边电场强度矢量,利用基函数线性插值得到空间任意一点的电场响应,最后通过法拉第电磁感应定律得到磁场分量响应。
2 算法验证 2.1 一维层状各向异性模型建立一个一维横向各向同性(VTI)模型[25](图 2),背景电导率为0.005 S∙m-1,各向异性低阻地层厚度为80 m,深度为50 m,其水平电导率均为0.1 S∙m-1,垂直电阻率为0.01 S∙m-1。矩形回线圈发射源边长为400 m,发射电流为1 A,测点A、B、C的坐标分别为(0,0,0)、(150 m, 150 m, 0)、(400 m, 400 m, 0)。时间窗口为1×10-5~1 s,采用不等间隔时间步长,在晚期加密时间采样个数。本文所有模型的空气电导率均为1×10-10 S∙m-1,计算区域大小为14 km×14 km×14 km,将发射线圈分为1200个等长线段。
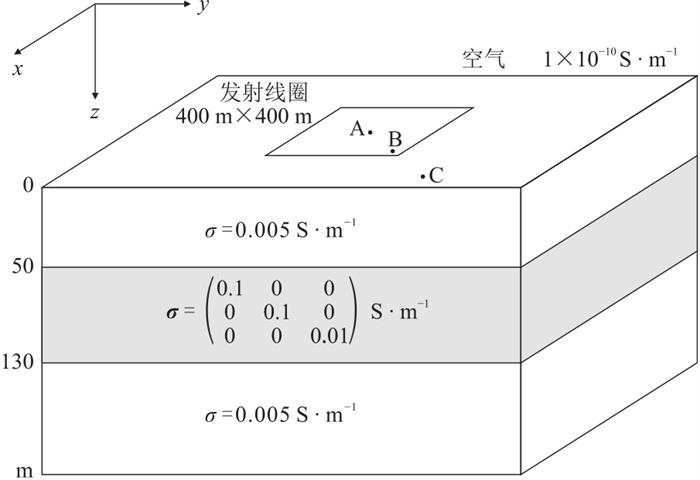
|
图 2 一维VTI模型示意图 |
图 3为三个测点处有限体积法(FVM)与有限单元法(FEM)的脉冲响应dBz/dt对比,可见这两种算法的响应曲线基本一致。不同于FVM,FEM是在整个区域内进行网格剖分计算,在2 ms附近,脉冲响应反号变化处的FEM结果的精度高于FVM,且实现了晚期响应的计算。
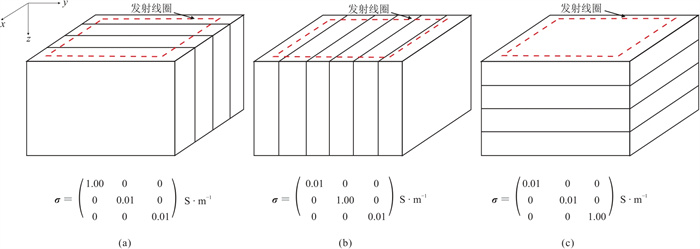
|
图 3 一维VTI模型dBz/dt响应曲线 |
建立一个回线源瞬变电磁三维各向异性半空间模型(图 4)[36]。回线源位于地表,边长为190 m,回线源中心位于坐标原点,发射电流为1 A,电流沿顺时针方向,脉冲持续时间为10 ms。测点位于(-60 m, -60 m, 0),记录参数为dBz/dt。模型中地层各向异性电阻率参数见图 4。

|
图 4 三维电导率各向异性半空间模型 (a)x轴各向异性;(b)y轴各向异性;(c)z轴各向异性 |
图 5为该回线源各向异性半空间模型的脉冲响应dBz/dt模拟结果。通过采用不等间距的时间步长,特别减小了10-4 s后的中晚期时间步长,可以观察到FEM与FDM的计算结果高度吻合,证明了本文方法的有效性,也反映了x轴与y轴电导率各向异性地层对dBz/dt响应的影响程度基本一致,验证了本文算法的正确性,确保了后续模型计算结果的可靠性。
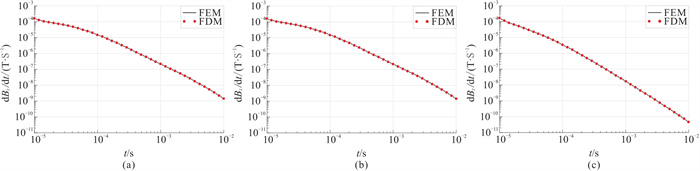
|
图 5 回线源三维各向异性模型dBz/dt数值模拟结果 (a)x轴各向异性;(b)y轴各向异性;(c)z轴各向异性 |
根据地—井瞬变电磁法勘探原理,建立图 6所示地—井各向异性瞬变电磁法方位测井模型。模型中竖直井的井径为10 cm,井深为1000 m,井中心位于坐标原点。井中泥浆电导率为1 S∙m-1。长导线源的长度为100 m,一端位于井口,另一端分别沿x轴正向、x轴反向、y轴正向、y轴反向布设。井中测线长度为200 m,测点沿井孔均匀布设,点距为10 m。
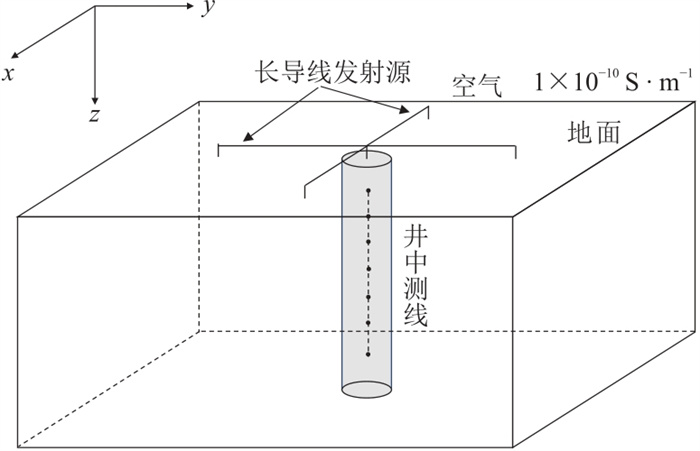
|
图 6 地—井各向异性瞬变电磁法方位测井模型示意图 |
网格剖分时,使用能够较好拟合复杂地质模型的自由四面体网格,并在发射长导线、井中测线和各向异性异常体处减小网格尺寸、加密网格,以提高计算精度。剖分后完整网格包含3227084个域单元、88062个边界单元和20424个边单元。井孔及其周围的网格剖分情况见图 7。计算过程在集群计算机上的一个节点上进行,该节点包括1个20核的CPU,计算时间为2400 s。
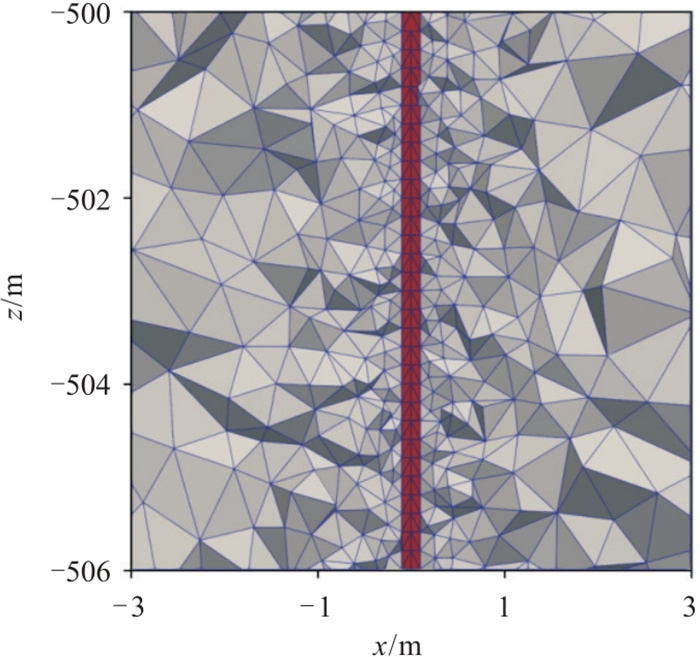
|
图 7 井孔网格剖分示意图 |
主轴各向异性地层的电导率参数见表 1。利用本文方法模拟分析不同方向发射源下、不同主轴方向(x轴、y轴和z轴)各向异性地层的瞬变电磁响应特征。
|
|
表 1 主轴各向异性模型参数 |
图 8为不同发射源方向下,测点(0,0,-500 m)处dBz/dt响应曲线。由图可见,当发射源方向与地层各向异性方向垂直时,dBz/dt响应最明显,具体表现在水平面上,当发射源方向与地层各向异性方向垂直时,dBz/dt随时间的变化趋势不变,但幅值变化显著。对于垂直各向异性地层,相比于发射源沿y轴方向,沿x轴方向布设发射源对应的dBz/dt响应幅值更大。
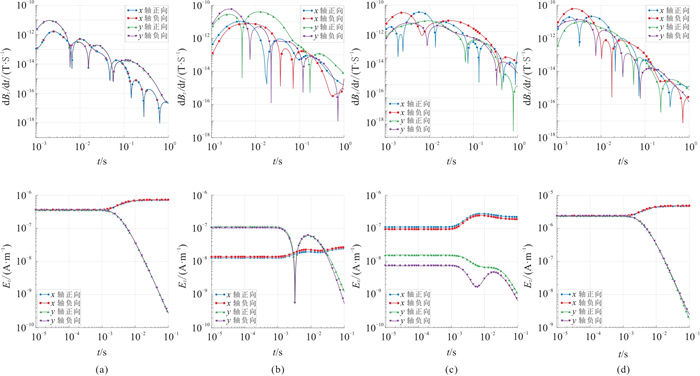
|
图 8 各向同性模型与各向异性模型的dBz/dt(上)和Ez(下)响应幅值差曲线 (a)各向同性模型;(b)x轴各向异性地层模型;(c)y轴各向异性地层模型;(d)z轴各向异性地层模型 |
与磁场响应dBz/dt不同,对于各向同性模型和各向异性模型,无论发射源沿哪个方向布设,电场分量Ez均呈现明显的对称特征(图 8下)。具体来说,当发射源沿同一直线上的两个相反方向布设时,Ez响应的幅值相等但符号相反。当地层为水平方向各向异性时,Ez曲线在10-4~10-1 s内变化显著,其变化规律与各向异性地层的dBz/dt响应相似。当发射源的布设方向与地层各向异性方向垂直时,Ez曲线的幅值响应最显著;相反,当发射源布设方向与地层各向异性方向平行时,Ez曲线的幅值变化则相对较小。当地层为垂直方向各向异性时,与地层为水平方向各向异性的情况相比,Ez曲线随时间的变化规律并未表现出显著的差异,仅在幅值上略有差别。
图 9为发射源沿不同方向布设时各向异性地层与各向同性地层响应幅值的差值。可以看出,dBz/dt和Ez响应差值曲线在10-3~10-1 s时间段内均发生了剧烈变化,其余时间段则保持了较稳定的值。由图 9(上)可见,当地层主轴各向异性方向与发射源方向垂直时,各向异性地层与各向同性地层的dBz/dt响应幅值差最显著,最大可达一个数量级,说明在特定角度下,地层各向异性对dBz/dt响应的影响显著。从图 9(下)可见,各向异性地层与各向同性地层Ez响应的幅值差也较大,但与dBz/dt响应的规律不同,呈现单调上升或者下降趋势。值得注意的是,在地层垂直各向异性条件下,对于四个不同方向发射源,Ez 响应幅值差均较大。
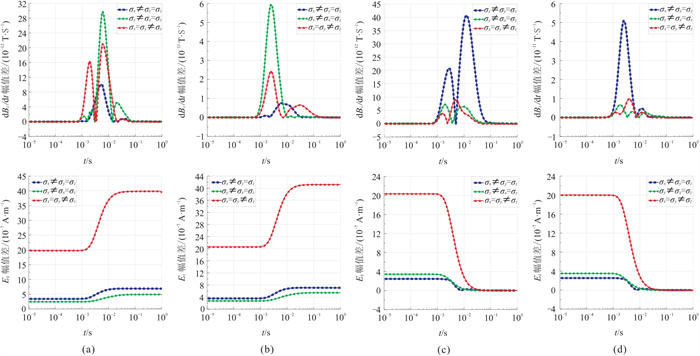
|
图 9 发射源沿不同方向布设时各向异性地层与各向同性地层dBz/dt(上)和Ez(下)响应幅值差曲线 (a)x轴正向;(b)x轴负向;(c)y轴正向;(d)y轴负向 |
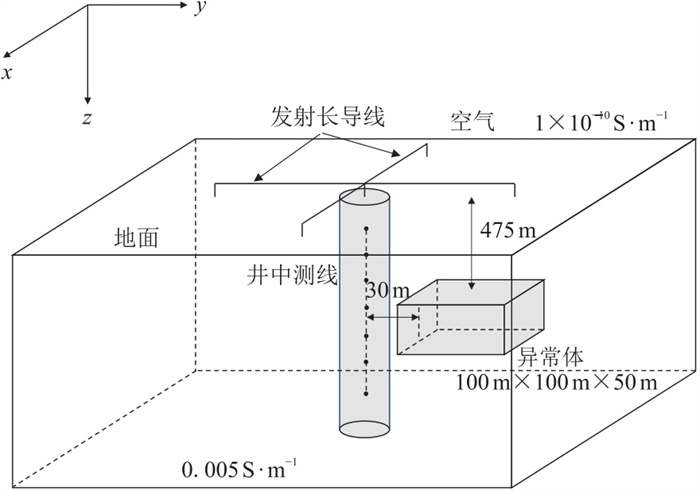
为进一步研究各向异性对地—井瞬变电磁响应的影响,在图 6所示模型中增加一个各向异性三维体,如图 10所示。在井旁水平方向30 m处设置一长100 m、宽100 m、高50 m的低阻异常体,其主轴电导率张量分别为
| $ {\boldsymbol{\sigma }}_{0}=\left(\begin{array}{ccc}0.1& 0& 0\\ 0& 0.1& 0\\ 0& 0& 0.1\end{array}\right)\mathrm{、}\left(\begin{array}{ccc}1.0& 0& 0\\ 0& 0.1& 0\\ 0& 0& 0.1\end{array}\right)\mathrm{、} \\ \left(\begin{array}{ccc}0.1& 0& 0\\ 0& 1.0& 0\\ 0& 0& 0.1\end{array}\right)\mathrm{、}\left(\begin{array}{ccc}0.1& 0& 0\\ 0& 0.1& 0\\ 0& 0& 1.0\end{array}\right)\mathrm{S}\cdot {\mathrm{m}}^{-1} $ |
|
图 10 主轴各向异性三维模型示意图 |
围岩电导率为0.005 S∙m-1;其余参数保持不变。
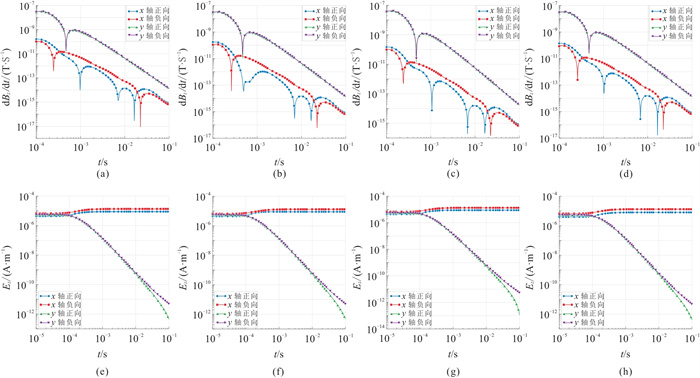
计算得到不同主轴方向各向异性异常体模型的电磁响应(图 11)。可以看出,井旁存在各向异性异常体时,dBz/dt响应和Ez响应随时间变化的趋势与各向同性异常体时基本一致。值得注意的是,当发射源沿y轴方向时,异常体模型的dBz/dt响应幅值变化较明显。然而,当发射源沿x轴方向展布时,即发射源展布方向与异常体相交的情况下,沿x轴负向展布的发射源较之于沿x轴正向展布的发射源,其产生的Ez响应更显著。尽管如此,无论发射源如何布置,Ez响应的对称特征都保持不变。
|
图 11 不同主轴各向异性异常体的响应 (a) 各向同性地层的dBz/dt响应;(b)x轴各向异性地层的dBz/dt响应;(c)y轴各向异性地层的dBz/dt响应;(d)z轴各向异性地层的dBz/dt响应;(e)各向同性地层的Ez响应;(f)x轴各向异性地层的Ez响应;(g)y轴各向异性地层的Ez响应;(h)z轴各向异性地层的Ez响应 |
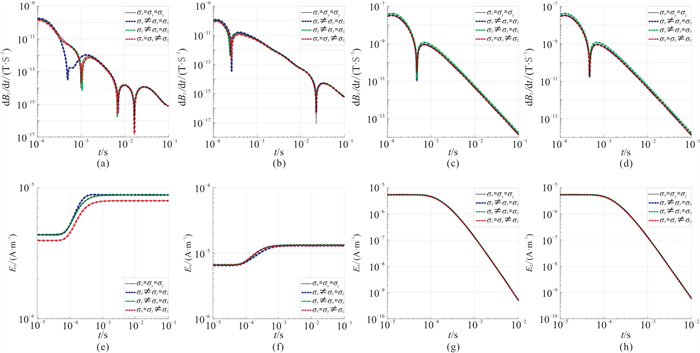
图 12展示了发射源沿不同方向布设时各向同性异常体模型和不同主轴各向异性异常体模型的磁场响应dBz/dt和电场响应Ez。对比各向同性模型的响应曲线,可以看出:对于磁场响应dBz/dt,当存在主轴各向异性异常体时,其影响主要集中在1×10-4 s附近,其影响范围较各向同性异常体更集中;主轴各向异性异常体在不同时间段内对电场Ez的影响则不同,表明异常体各向异性对电场的影响较磁场更复杂。
分析图 12a、图 12b、图 12e、图 12f可见,与发射源沿y轴布设相比,当发射源沿x轴布设时,主轴各向异性异常体的dBz/dt响应和Ez响应幅值更大。同时,当发射源方向与异常体主轴各向异性方向在水平面的投影相交时,与两者方向不相交的情况相比,磁场的时间变化率dBz/dt以及电场分量Ez在识别并区分具有显著各向异性特征的异常体方面表现出了更强的分辨能力。
|
图 12 发射源沿不同方向布设时的各向异性模型电磁响应 (a) 发射源沿x轴正向时的dBz/dt响应;(b)发射源沿x轴负向时的dBz/dt响应;(c)发射源沿y轴正向时的dBz/dt响应;(d) 发射源沿y轴负向时的dBz/dt响应;(e)发射源沿x轴正向时的Ez 响应;(f)发射源沿x轴负向时的Ez 响应;(g)发射源沿y轴正向时的Ez 响应;(h)发射源沿y轴负向时的Ez 响应 |
对比分析图 12c、图 12d、图 12g与图 12h可见,当发射源的布设方向与地下异常体电性主轴在水平面上的投影不重合或形成显著夹角时,异常体的主轴各向异性特征在dBz/dt及Ez响应曲线上反应并不明显,甚至在某些时间区间,这些电磁响应几乎无法有效表征异常体的存在,增加了探测与识别的难度。特别值得注意的是,只有当异常体的主轴各向异性方向与发射源方向在水平面上的投影近乎平行时,dBz/dt的幅值才会发生显著变化,这一变化明显体现了异常体各向异性特性。这一结论不仅有助于理解电磁场与地下复杂结构相互作用的机制,还可以为地—井瞬变电磁勘探提供实践指导,即在探测过程中,合理选择发射源的方向,使之与预期异常体的主轴各向异性方向平行,这样能够显著提高探测的灵敏度和准确性,为地—井瞬变电磁法在地质勘探、矿产资源勘探等领域的应用带来显著的优势。
由以上分析可以看出,在发射源沿不同方向布设条件下,异常体主轴各向异性对Ez响应的影响依旧显著。发射源的方向与异常体各向异性方向相互垂直时,Ez响应的幅值会呈现出明显变化;当发射源的方向与地层各向异性方向一致时,各向异性异常体对Ez响应的影响几乎可以忽略不计。这一结论与前文(3.1节)关于各向异性层状地层模型所得到的结论吻合,进一步证实了层状/三维体各向异性对地—井瞬变电磁探测结果的影响较大。
4 实际应用图 13为加拿大拉布拉多省卵型体镍铜硫化矿区钻孔勘查模型[37],利用该模型验证复杂各向异性异常矿体对地—井瞬变电磁响应的影响。复杂矿体规模约为400 m×300 m×150 m,其上覆盖层厚度为20 m,围岩电导率为0.0001 S∙m-1,高导矿脉电导率为100 S ∙ m-1,假设其电导率各向异性为
| $ {\boldsymbol{\sigma }}_{0}=\left(\begin{array}{ccc}100& 0& 0\\ 0& 100& 0\\ 0& 0& 100\end{array}\right)\mathrm{、}\left(\begin{array}{ccc}10& 0& 0\\ 0& 100& 0\\ 0& 0& 100\end{array}\right)\mathrm{、} \\\left(\begin{array}{ccc}100& 0& 0\\ 0& 10& 0\\ 0& 0& 100\end{array}\right)\mathrm{、}\left(\begin{array}{ccc}100& 0& 0\\ 0& 100& 0\\ 0& 0& 10\end{array}\right)\mathrm{S}\mathrm{ }\bullet {\mathrm{m}}^{-1} $ |

|
图 13 卵状带块状硫化物矿体模型(a)及网格剖分(b) 蓝色圆柱体表示井模型,红色线段表示地表长导线发射源。 |
井孔位于模型中心,其坐标为(555700 m, 6243200 m, 110 m),井坐标为(-100 m, -50 m, 80 m),井深为200 m。发射源长度为200 m,分别沿东、西、南、北四个方向布设。测线位于井中,长度为200 m,测点间距为10 m。该型空间剖分为2287052个域单元、64376个边界单元和16805个边单元(图 13b)。
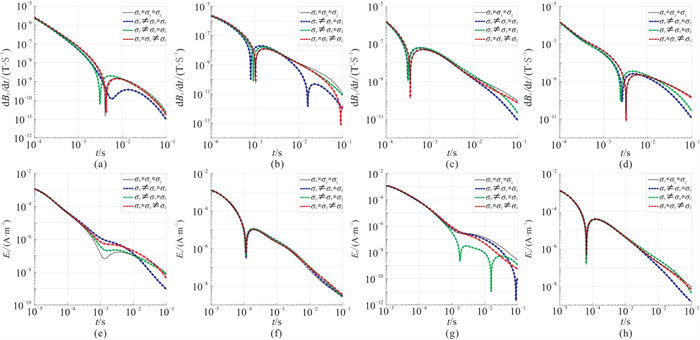
测点位于地面,其坐标为(-100 m, -50 m, 0)。发射源沿不同方向条件下,模型主轴各向异性异常体所产生的dBz/dt与Ez 响应见图 14。由图可见,当发射源方向与异常体主轴各向异性方向在水平面上垂直时,磁场响应dBz/dt表现突出;仅在发射源方向与异常体主轴各向异性方向在地面的投影相交时,异常体的各向异性对电场响应Ez的影响显著增强(图 14e、图 14g),在这一特定条件下,各向异性对电场分布的影响尤为明显。
|
图 14 不同方向发射源下卵状带块状硫化物矿体模型的电磁响应 (a)发射源沿x轴正向的dBz/dt响应;(b)发射源沿x轴负向的dBz/dt响应;(c)发射源沿y轴正向的dBz/dt响应;(d) 发射源沿y轴负向的dBz/dt响应;(e)发射源沿x轴正向的Ez 响应;(f)发射源沿x轴负向的Ez 响应;(g)发射源沿y轴正向的Ez 响应;(h)发射源沿y轴负向的Ez 响应 |
图 15为t=0.01 s时刻发射源沿不同方向时,主轴各向异性异常体的dBz/dt和Ez 响应曲线。这些曲线表现出与单个测点的观测结果类似的变化规律,进一步证实了“当发射源方向与主轴各向异性方向在水平面上垂直时,磁场响应最为明显”这一结论,这点充分体现在井中沿深度上不同测点的处理结果上,尤其是当发射源与异常体在地面的投影相交时,各测点所对应的Ez 响应曲线均能显著地体现出各向异性特征。
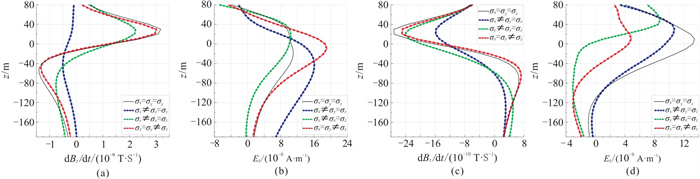
|
图 15 t=0.01 s时刻卵状带块状硫化物矿体模型的电磁响应 (a)发射源沿x轴正向时的dBz/dt响应;(b)发射源沿x轴正向时的Ez 响应;(c) 发射源沿y轴正向时的dBz/dt响应;(d)发射源沿y轴正向时的Ez 响应 |
地—井瞬变电磁电磁响应特征受地层各向异性方向与发射源方向的相交关系的影响。在水平面上,当主轴各向异性方向与长导线发射源布设方向垂直时,电磁场响应最明显;当主轴各向异性的方向与长导线发射源布设方向平行时,电磁场响应的幅值随时间变化趋势相对较为平缓。在识别垂直方向的各向异性特征上,磁场响应dBz/dt表现出比电场响应Ez 更强的分辨能力。
基于加拿大拉布拉多省卵型体镍铜硫化矿区钻孔勘查模型,分析了各向同性地层中的各向异性异常体对电磁场响应的影响,得到以下结论。
(1) 电磁场响应特征与异常体各向异性方向和发射源方向有关:当发射源方向与异常体各向异性方向相交时,电磁场对主轴各项异性异常体的分辨能力较强;当发射源方向与异常体各向异性方向不相交时,磁场响应最明显,但只能辨别特定方向的主轴各向异性异常体。
(2) 与各向同性异常体响应比,当发射源方向与异常体各向异性方向在某一平面内相交时,电磁响应对各向异性异常体的分辨能力明显提升。然而,主轴各向异性异常体对脉冲响应的影响仅在部分时间段内表现显著,可能会增加反演问题的复杂性和挑战性,这一特性在反演解释时需要特别关注。
为了深入探索储层的复杂性和非均质性,为地下资源的精准勘探与开发提供关键的地质信息与参数,为油气勘探、水资源评价等领域的战略决策提供技术支撑,各向异性介质的地—井瞬变电磁数据的三维反演技术是关键。虽然电磁法勘探已取得一定进展,但由于设备限制、试验井等实际条件的约束,地—井瞬变电磁勘探的实际工作经验较缺乏,因此难于获取足够多的实测数据,使得基于地—井瞬变电磁法的三维反演技术面临巨大挑战。因此,需继续深入研究基于各向异性介质的地—井瞬变电磁三维数据反演方法,对于推动地质勘探技术的创新与发展具有重要的意义和必要性。
感谢纽芬兰纪念大学的Farquharson教授提供的卵形体镍铜硫化矿区钻孔模型。
| [1] |
臧德福, 朱留方, 张付明, 等. 瞬变电磁测井原理研究Ⅲ: 电磁波[J]. 测井技术, 2014, 38(5): 530-534. ZANG Defu, ZHU Liufang, ZHANG Fuming, et al. Theory study for transient electromagnetic logging Ⅲ: electromagnetic wave[J]. Well Logging Technology, 2014, 38(5): 530-534. |
| [2] |
王新宇, 严良俊, 毛玉蓉. 电性源瞬变电磁法油气藏动态监测模拟分析[J]. 石油地球物理勘探, 2022, 57(2): 459-466. WANG Xinyu, YAN Liangjun, MAO Yurong. Simulation and analysis of dynamic monitoring of oil and gas reservoir based on grounded electric source TEM[J]. Oil Geophysical Prospecting, 2022, 57(2): 459-466. |
| [3] |
王少杰, 周磊, 谢兴兵, 等. 基于差分进化算法的瞬变电磁一维反演[J]. 石油地球物理勘探, 2024, 59(2): 343-351. WANG Shaojie, ZHOU Lei, XIE Xingbing, et al. Transient electromagnetic one‑dimensional inversion based on differential evolution algorithm[J]. Oil Geophysical Prospecting, 2024, 59(2): 343-351. |
| [4] |
易洪春. 地—井瞬变电磁响应特征研究[J]. 物探与化探, 2018, 42(5): 970-976. YI Hongchun. Research on response of ground-borehole TEM[J]. Geophysical and Geochemical Exploration, 2018, 42(5): 970-976. |
| [5] |
郜杰. 瞬变电磁测井方法试验研究[J]. 能源技术与管理, 2016, 41(2): 179-180. GAO Jie. Experimental study on transient electromagnetic logging method[J]. Energy Technology and Management, 2016, 41(2): 179-180. |
| [6] |
BAILEY J, LAFRANCEB, MCDONALD M A, et al. Mazatzal labradorian-age (1.7-1.6 Ga) ductile deformation of the South Range Sudbury impact structure at the Thayer Lindsley mine, Ontario[J]. Canadian Journal of Earth Sciences, 2004, 41(12): 1491-1505. |
| [7] |
MOLNAR F, WATKINSON D H, JONES P C. Fluid inclusion evidence for hydrothermal enrichment of magmatic ore at the contact zone of the Ni-Cu-platinum‑group element 4b Deposit, Lindsley Mine Sudbury, Canada[J]. Economic Geology, 1997, 92(6): 674-685. |
| [8] |
地—井瞬变电磁法技术规程: DD 2019-11[S]. 北京: 自然资源部中国地质调查局, 2019, 2-3. Technical Specification for Borehole Transient Electromagnetic Method: DD 2019-11[S]. China Geological Survey, Ministry of Natural Resources, Beijing, China, 2019, 2-3. |
| [9] |
KLEIN J D, MARTIN P R, ALLEN D F. The petrophysics of electrically anisotropic reservoirs[J]. The Log Analyst, 1997, 38(3): 25-36. |
| [10] |
OBRIEN D P, MORRISON H F. Electromagnetic fields in an n‑layer anisotropic half space[J]. Geophysics, 1967, 32(4): 668-677. |
| [11] |
WEISS C J, NEWMAN G A. Electromagnetic induction in a fully 3‑D anisotropic earth[J]. Geophysics, 2002, 67(4): 1104-1114. |
| [12] |
PEK J, SANTOS F A M. Magnetotelluric impe-dances and parametric sensitivities for 1-D anisotropic layered media[J]. Computers & Geosciences, 2002, 28(8): 939-950. |
| [13] |
邓少贵, 刘天淋, 王磊, 等. 双轴各向异性介质多分量感应测井响应快速计算[J]. 地球物理学报, 2020, 63(1): 362-373. DENG Shaogui, LIU Tianlin, WANG Lei, et al. Analytical solution of multi-component induction logging response in biaxial anisotropic medium[J]. Chinese Journal of Geophysics, 2020, 63(1): 362-373. |
| [14] |
PEK J, SANTOS F. Magnetotelluric impedances and parametric sensitivities for 1-D anisotropic layered media[J]. Computers & Geosciences, 2002, 28(8): 939-950. |
| [15] |
李海, 薛国强, 钟华森, 等. 多道瞬变电磁法共中心点道集数据联合反演[J]. 地球物理学报, 2016, 59(12): 4439-4447. LI Hai, XUE Guoqiang, ZHONG Huasen, et al. Joint inversion of CMP gathers of multi-channel transient electromagnetic data[J]. Chinese Journal of Geophysics, 2016, 59(12): 4439-4447. |
| [16] |
徐世浙, 赵生凯. 二维各向异性地电断面大地电磁场的有限元法解法[J]. 地震学报, 1985, 7(1): 80-90. XU Shizhe, ZHAO Shengkai. Solution of magnetotelluric field equations for a two‑dimensional, anisotropic geoelectric section by the finite element method[J]. Acta Seismologica Sinica, 1985, 7(1): 80-90. |
| [17] |
YU L, EVANS R L, EDWARDS R N. Transient electromagnetic responses in seafloor with triaxial anisotropy[J]. Geophysical Journal International, 1997, 129(2): 292-304. |
| [18] |
王昌学, 周灿灿, 储昭坦, 等. 电性各向异性地层频率域电磁响应模拟[J]. 地球物理学报, 2006, 49(6): 1873-1883. WANG Changxue, ZHOU Cancan, CHU Zhaotan, et al. Modeling of electromagnetic responses in frequency domain to electrical anisotropic formations[J]. Chinese Journal of Geophysics, 2006, 49(6): 1873-1883. |
| [19] |
孙向阳, 聂在平, 赵延文, 等. 用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应[J]. 地球物理学报, 2008, 51(5): 1600-1607. SUN Xiangyang, NIE Zaiping, ZHAO Yanwen, et al. The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method[J]. Chinese Journal of Geophysics, 2008, 51(5): 1600-1607. |
| [20] |
陈桂波, 汪宏年, 姚敬金, 等. 用积分方程法模拟各向异性地层中三维电性异常体的电磁响应[J]. 地球物理学报, 2009, 52(8): 2174-2181. CHEN Guibo, WANG Hongnian, YAO Jingjin, et al. Modeling of electromagnetic responses of 3-D electrical anomalous body in a layered anisotropic earth using integral equations[J]. Chinese Journal of Geophysics, 2009, 52(8): 2174-2181. |
| [21] |
DENNIS Z R, CULL J P. Transient electromagnetic surveys for the measurement of near-surface electrical anisotropy[J]. Journal of Applied Geophysics, 2012, 76: 64-73. |
| [22] |
严良俊, 周磊, 谢兴兵, 等. 储层电各向异性模型的瞬变电磁响应[J]. 工程地球物理学报, 2014, 11(3): 346-350. YAN Liangjun, ZHOU Lei, XIE Xingbing, et al. The transient electromagnetic response of electrical anisotropic reservoir model[J]. Chinese Journal of Engineering Geophysics, 2014, 11(3): 346-350. |
| [23] |
王煜翔. 各向异性介质中的电性源瞬变电磁一维正反演方法研究[D]. 四川成都: 电子科技大学, 2019. WANG Yuxiang. Research on One-Dimension Forward and Inversion Method of Grounded Electrical-Source Transient Electromagnetic in Anisotropic Medium[D]. University of Electronic Science and Technology of China, Chengdu, Sichuan, 2019. |
| [24] |
周建美, 刘文韬, 李貅, 等. 双轴各向异性介质中回线源瞬变电磁三维拟态有限体积正演算法[J]. 地球物理学报, 2018, 61(1): 368-378. ZHOU Jianmei, LIU Wentao, LI Xiu, et al. Research on the 3D mimetic finite volume method for loop-source TEM response in biaxial anisotropic formation[J]. Chinese Journal of Geophysics, 2018, 61(1): 368-378. |
| [25] |
刘亚军, 胡祥云, 彭荣华, 等. 回线源瞬变电磁法有限体积三维任意各向异性正演及分析[J]. 地球物理学报, 2019, 62(5): 1954-1968. LIU Yajun, HU Xiangyun, PENG Ronghua, et al. 3D forward modeling and analysis of the loop-source transient electromagnetic method based on the finite-volume method for an arbitrarily anisotropic medium[J]. Chinese Journal of Geophysics, 2019, 62(5): 1954-1968. |
| [26] |
刘亚军. 时间域电磁法三维各向异性正演及分析[D]. 湖北武汉: 中国地质大学(武汉), 2020. LIU Yajun. Three‑dimensional Forward Modeling and Analysis of Time‑Domain Electromagnetic Data for an Anisotropic Medium[D]. China University of Geosciences(Wuhan), Wuhan, Hubei, 2020. |
| [27] |
郭建磊, 姜涛, 郭恒, 等. 轴向各向异性地—井瞬变电磁三分量响应特征[J]. 地球科学与环境学报, 2020, 42(6): 737-748. GUO Jianlei, JIANG Tao, GUO Heng, et al. Characteristics of axial anisotropic borehole transient electromagnetic three-component response[J]. Journal of Earth Sciences and Environment, 2020, 42(6): 737-748. |
| [28] |
郭建磊, 高小伟, 侯彦威. 轴向各向异性巷—孔瞬变电磁三分量响应特征研究[J]. 煤田地质与勘探, 2022, 50(7): 52-62. GUO Jianlei, GAO Xiaowei, HOU Yanwei. Research on three-component responses characteristics of axial anisotropy tunnel‑hole transient electromagnetic[J]. Coal Geology & Exploration, 2022, 50(7): 52-62. |
| [29] |
LI H, MAO Y, WANG X, et al. Characterization of Surface-Borehole transient electromagnetic response in electrical anisotropic media[J]. Minerals, 2023, 13(5): 674. |
| [30] |
牛之琏. 时间域电磁法原理[M]. 湖南长沙: 中南工业大学出版社, 2007. NIU Zhilian. Principle of Electromagnetic Method in Time Domain[M]. Changsha, Hunan: Central-South University of Technology Press, 2007. |
| [31] |
YIN C C. Geoelectrical inversion for a one-dimensional anisotropic model and inherent non-uniqueness[J]. Geophysical Journal International, 2000, 140(1): 11-23. |
| [32] |
PEK J, SANTOS F A M. Magnetotelluric inversion for anisotropic conductivities in layered media[J]. Physics of the Earth & Planetary Interiors, 2006, 158(2-4): 139-158. |
| [33] |
刘云鹤, 殷长春, 蔡晶, 等. 电磁勘探中各向异性研究现状和展望[J]. 地球物理学报, 2018, 61(8): 3468-3487. LIU Yunhe, YIN Changchun, CAI Jing, et al. Review on research of electrical anisotropy in electromagnetic prospecting[J]. Chinese Journal of Geophysics, 2018, 61(8): 3468-3487. |
| [34] |
UM E S, HARRIS J M, ALUNBAUGH D L. 3D time-domain simulation of electromagnetic diffusion phenomena: a finite-element electric-field approach[J]. Geophysics, 2010, 75(4): F115-F126. |
| [35] |
于超. 大规模稀疏矩阵PARDISO求解方法介绍[J]. 高性能计算发展于应用, 2016(4): 13-15. YU Chao. Introduction of PARDISO solution method for large‑scale sparse matrix[J]. High‑Performance Computing Is Evolving in Applications, 2016(4): 13-15. |
| [36] |
郭建磊. 轴向各向异性地层瞬变电磁三分量响应特征[J]. 物探与化探, 2022, 46(2): 362-372, 382. GUO Jianlei. Three-component responses of axially anisotropic formations using the transient electromagnetic method[J]. Geophysical and Geochemical Exploration, 2022, 46(2): 362-372, 382. |
| [37] |
LI J, HU X, CAI H, et al. A finite-element time-domain forward-modelling algorithm for transient electromagnetics excited by grounded-wire sources[J]. Geophysical Prospecting, 2020, 68(4): 1379-1398. |



 毛玉蓉, 湖北省武汉市蔡甸区蔡甸街大学路111号,430100。Email:
毛玉蓉, 湖北省武汉市蔡甸区蔡甸街大学路111号,430100。Email: