2. 中国地质科学院地球物理地球化学勘查研究所, 河北廊坊 065000;
3. 东方地球物理公司采集技术中心, 河北涿州 072751
2. Institute of Geophysical and Geochemical Exploration, Chinese Academy of Geological Sciences, Langfang, Hebei 065000, China;
3. Acquisition Technology Institute, BGP Inc., CNPC, Zhuozhou, Hebei 072751, China
大地电磁测深法是一种以天然电磁场作为场源的地球物理勘探方法,该方法探测深度大、装备轻便、成本低,在地球深部探测中发挥了重要作用[1-5]。大地电磁数据反演是数据处理的关键环节。常规的大地电磁反演方法(如:非线性共轭梯度反演[6]、Occam反演[7]等)都需要计算雅可比矩阵,反演效率低,对初始模型依赖性强。随着深度学习理论的不断发展,基于深度神经网络的大地电磁反演能够对大量的正演模型与电阻率网格的对应关系进行自主学习,无需依赖初始模型,避免了灵敏度矩阵的计算,取得了很好的反演效果,在地球物理反演领域得到快速发展[8-14]。为了提高神经网络反演性能,可以适当增加神经网络的层数,但若层数过多,会出现梯度消失/爆炸问题,导致准确度下降。He等[15]提出ResNet残差网络,缓解了深度神经网络中增加深度带来准确度下降的问题。Liu等[16]提出了基于残差卷积神经网络的一维音频大地电磁数据反演方法,李梦迪[17]开展了基于残差网络的大地电磁一维反演研究,这些研究都较准确地恢复了地下电性结构。Guo等[18]利用一种深度残差卷积网络实现了音频大地电磁数据与地震数据的联合反演。基于残差神经网络的优势,本文开展了大地电磁二维反演研究,在神经网络的基础上加入了残差模块,以TE、TM极化模式下的视电阻率与相位数据作为四通道输入,对应的地电模型作为输出,进行有监督的学习,实现了基于残差卷积神经网络的二维大地电磁反演,提高了反演结果的可靠性。最后将该方法应用于冀中坳陷实测电磁数据的反演。
1 方法原理通常情况下使用标准优化算法训练一个普通网络,在面对复杂问题时,网络越深往往性能更佳。然而,实践证明随着网络的加深,出现了训练准确度下降的现象,这并不是过拟合引起的,而是由于梯度的消失/爆炸导致的。针对这个情况,本文利用一种加入残差的深度网络消除网络加深带来的准确度下降。
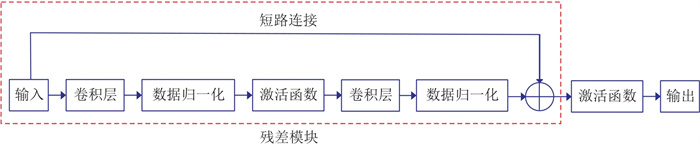
1.1 残差网络基本原理残差块是残差网络重要的组成部分,也是区别于传统卷积神经网络的重要结构[19](图 1),这个结构称为残差模块。在残差块中最后一层卷积层后并没有激活函数,而是在与输入相加后再连接激活函数,这个过程称为恒等映射[20]。恒等映射是在输出和输入之间引入一个短路连接,在应用激活函数之前将输入添加到输出。若需要输出等于输入,只需将残差函数设置为0。相比于传统卷积神经网络,该方法实现输出等于输入的过程更简单,并可有效改善深层网络的性能。
|
图 1 残差模块示意图 |
在残差块内卷积层通过卷积操作可以对输入进行降维和特征提取。神经网络前部分的卷积层是小的感受野,负责捕捉输入的低级特征,然后输出激活值[21]。后部分的卷积层感受野逐层加大,用于捕捉、输入更复杂、抽象的信息。经过多个卷积层运算,得到输出值。通过卷积层卷积可完成输入的降维和特征提取,若特征图像的维度仍然很高,则可采用池化层,目的是提高计算速度,降低过拟合的概率,提升特征提取的鲁棒性。
对于卷积层特征提取,由于卷积操作是线性的且效果不佳,因此,需要进行非线性边界拟合,所以激活函数是关键环节。目前有很多非线性激活函数,常见的有Sigmoid、Tanh、ReLU等。最常用的是ReLU激活函数,该激活函数收敛速度快、计算成本相对较低,在反向传播过程中更容易优化,同时解决了Sigmoid激活函数局部梯度消失/爆炸的问题[22]。ReLU激活函数为
| $ f\left(x\right)=\mathrm{m}\mathrm{a}\mathrm{x}(0,x) $ | (1) |
式中x为输入。
1.2 基于残差网络的大地电磁数据反演残差网络可以利用正演模拟得到的地电模型和观测响应作为训练数据集,对每一组地电模型与观测响应中学习其对应关系,建立视电阻率和相位与电阻率模型的非线性映射,并在训练过程中不断更新参数权重,最终得到一个适合该训练数据集的网络。
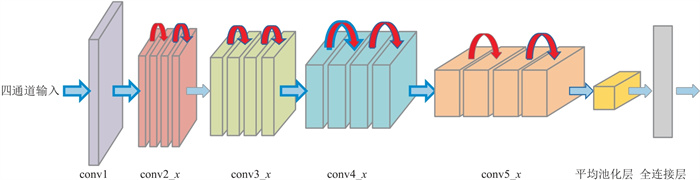
目前主流残差神经网络主要应用于图像识别,处理对象是图片,输入是像素点[23]。大地电磁二维正演的结果是各测点的视电阻率和相位,所以一个观测数据可以看作一个像素点。图像处理中,不同颜色对应一个通道数。相应地,TE模式和TM模式下的视电阻率与相位则对应四个通道,可作为网络输入,地电模型则可视为网络输出。一套正演观测数据对应一个地电模型,输入残差神经网络进行有监督的学习。本文基于ResNet-18网络结构设计了适用于大地电磁数据二维反演的优化残差网络,ResNet-18比更深的残差网络训练时间短,参数较少,不易过拟合[24]。网络主要包含五个阶段(图 2):第1阶段(conv1)包含卷积层、标准化层、ReLU激活函数、最大池化层;第2~5阶段(conv2_x ~ conv5_x)中,每个阶段均包含2个残差模块,每个残差模块内有2次卷积。五个阶段结束后,进入全局平均池化层[25]。最后进入全连接层,输出结果。网络经过对大量的数据集进行训练,得到优化参数网络。将视电阻率与相位数据输入训练好的网络,得到对应的电阻率模型。残差网络训练效果可通过均方误差[26]进行评价
| $ \mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{n}\sum\limits_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i}{)}^{2} $ | (2) |
|
图 2 基于残差网络的大地电磁反演图 conv1表示第1阶段,conv2_x~conv5_x表示第2~第5阶段。 |
式中:n为反演数据的个数;yi为测试集模型的理论值归一化结果;
基于有限元大地电磁二维正演获得数据集。正演过程中,目标区域剖分网格个数设置为40×30,网格采用可变网格,中间和浅部网格剖分密集,两边及深部剖分稀疏。设正演测点数为38,频点数为60,频率范围10-4~103 Hz。
用于训练神经网络模型参数的数据集的数量和质量对于反演的准确性至关重要,充足的数据集可以使残差网络反演更准确。本文共建立了20000个数据集,包括10000个标准模型数据集和10000个针对性模型数据集。标准模型数据集包括常见的低阻异常体模型、高阻异常体模型、高—低阻组合模型、背斜模型、向斜模型、断层模型、组合模型等七大类。
为了使数据集更全面、适用性强,在建立异常体为块体模型的数据集时,通过扰动不断改变异常体的空间位置、大小、电阻率及背景电阻率来扩充数据集。改变异常体的位置时其他参数保持不变,将异常体从目标区域按照一定步长沿上、下、左、右移动,遍历所有网格。通常来说,异常体的电阻率低值范围为5~50 Ω·m,高值范围为500~10000 Ω·m,背景电阻率范围为50~200 Ω·m,据此建立低阻异常体模型、高阻异常体模型及高—低阻组合模型共3000个。在建立层状模型数据集时,随机改变模型的层厚度、每层的电阻率及背景电阻率,扩充数据集。本文地层电阻率变化范围设置为10~1000 Ω·m,据此建立背斜模型、向斜模型、断层模型共3500个。基于层状模型,局部随机填充不同的高阻块体或者低阻块体,建立组合模型,此次研究共建立了3500个组合模型。
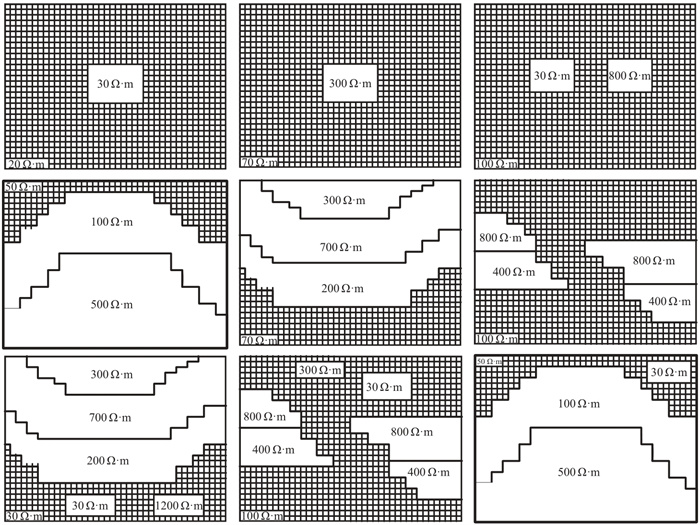
为了进一步增加样本的多样性,在一些模型中加入5%的高斯噪声,以此提升网络的泛化能力。由于数据集数量庞大,基于程序进行循环正演,得到不同电阻率模型的TE模式和TM模式下的视电阻率与相位。图 3为部分模型的电阻率分布。
|
图 3 部分模型示意图 |
基于先验信息建立能反映地下基本构造特征的模型数据集,可提高反演的效率和精度。本文对输入数据开展大地电磁一维快速反演,进一步扰动电阻率及异常体位置,建立10000个有针对性的模型进行正演,形成更完备和合理的数据集。
2.2 反演训练本文的残差网络模型是基于Pytorch框架构建的。基于准备的数据集,以地电模型为标签,正演TE、TM模式下的视电阻率和相位,以此作为样本训练。训练中以TE、TM模式下的视电阻率和相位数据作为四通道输入,确保训练结果的可靠性。将大地电磁TE、TM模式的视电阻率和相位数据(矩阵大小为4×38×61,其中TE模式和TM模式下的视电阻率和相位数据大小为4,观测点数为38,频点数为61)输入残差网络,在第1阶段基于7×7卷积层进行特征提取,在标准化层加快模型训练收敛速度,在最大池化层进行降维。之后的四个阶段,每个阶段包含2个残差块,每个残差块有两层3×3的卷积,最后连上一个全连接层,输出的神经元个数为40×30。训练过程中的网络参数设置很重要,会直接影响网络的反演效果。基于样本数据,设置了多组参数进行误差对比,进行最优参数的选取,其参数最佳设置为:batch_size=200,learning_rate=1×10-4,num_epoches=500,Dropout=0.1,训练优化器为Adam,激活函数为ReLU。训练过程中,将数据集按8∶2的比例分为训练集和验证集,训练集负责根据样本和标签进行有监督的训练,验证集不参与训练,只用于评估网络训练的效果。训练结果使用均方误差进行评价。
2.3 模型反演针对大地电磁场的TE与TM模式,设置简单模型和复杂模型进行反演训练,通过损失函数判断反演结果好坏,训练中加入噪声,以分析残差网络反演算法的抗噪能力。
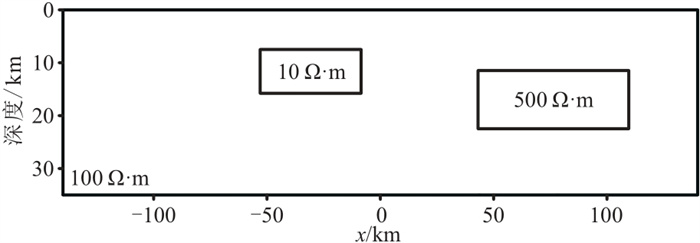
2.3.1 简单模型建立图 4所示简单地电模型,其背景为均匀半空间。电阻率为100 Ω·m,模型包括一个高阻异常体和一个低阻异常体,其大小分别为70 km×10 km和40 km×5 km。
|
图 4 简单模型示意图 |
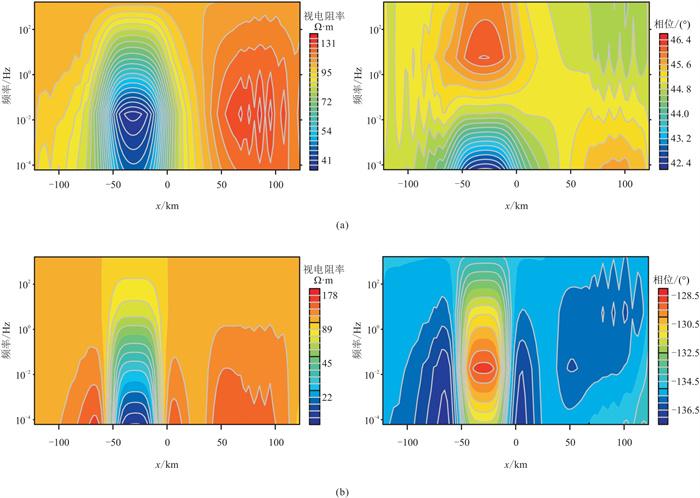
图 5为TE模式与TM模式下的正演视电阻率和相位剖面。由图可见,模型电阻率及相位分布可大致反映电阻率异常体的分布。
|
图 5 图 4模型TE模式(a)和TM模式(b)下的正演视电阻率(左)和相位(右)剖面 |
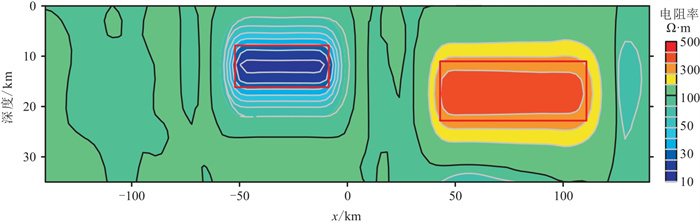
利用该模型数据集进行正演模拟。将TE模式和TM模式下不同频率对应的视电阻率和相位以及模型网格数字化数据输入残差网络进行训练,然后对模型视电阻率和相位进行反演。基于残差网络算法的反演结果见图 6,其均方误差为0.540990。由图可见,电阻率反演剖面很好地恢复了异常体的位置,高阻异常体和低阻异常体的位置及电阻率均与模型基本吻合,说明反演结果是准确的,同时也证明高达18层的残差网络并不会因为层数过多而降低网络的准确性。
|
图 6 图 4模型基于残差网络算法的电阻率反演剖面 |
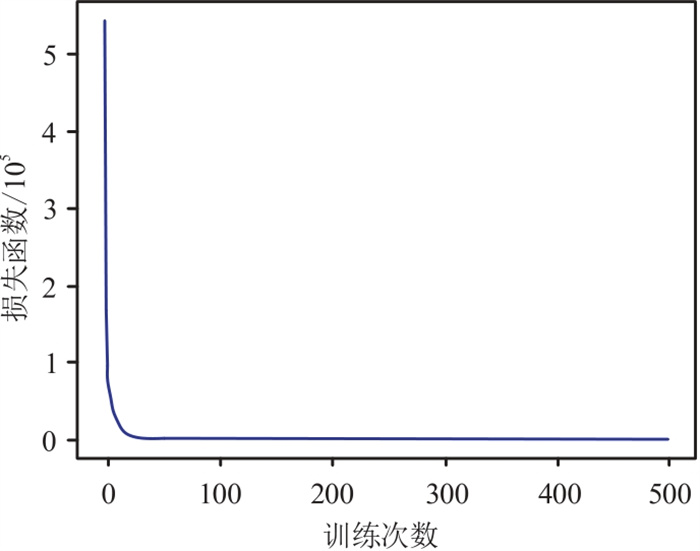
图 7为图 4模型反演拟合损失函数值,据此可评价神经网络反演拟合结果。可以看出,随着训练次数增加,损失函数值逐渐降低,训练达到500次时,损失函数值达到最小,说明训练后的网络不断优化,最终趋于一个稳定的很小值。
|
图 7 图 4模型反演拟合损失函数曲线 |
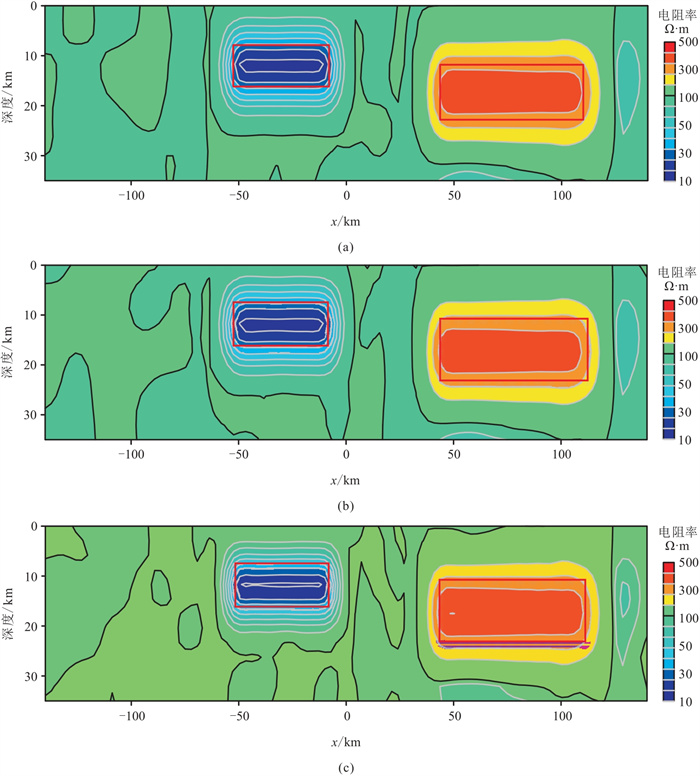
为了进一步验证残差网络的稳定性,对数据进行加噪处理,分别加入5%、10%、15%的噪声,进行残差网络反演,反演结果如图 8所示,对应的训练结果均方误差分别为0.543525、0.523759和0.539654,二者基本一致,验证了残差网络训练结果的可靠性。
|
图 8 图 4模型加噪数据电阻率反演剖面 (a)加噪5%;(b)加噪10%;(c)加噪15% |
对比图 8与图 6可以看出,加噪数据反演结果中只有背景电阻率发生明显变化,加入的噪声水平越高,背景电阻率变化越明显,但高阻异常体和低阻异常体的位置、大小及电阻率基本不受影响。加噪数据反演结果说明残差网络的抗噪能力较强。
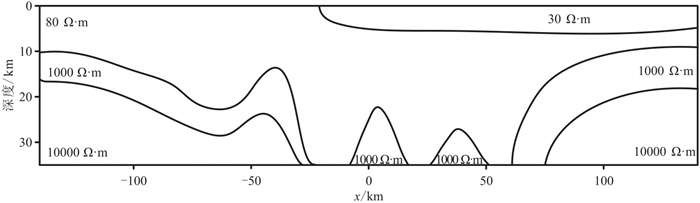
2.3.2 复杂模型为了分析本文方法对复杂模型的反演效果,基于冀中坳陷深部热储模型建立图 9所示复杂模型。模型中电阻率为80 Ω·m的区域即是电阻率异常区域,其上为一条低阻地热通道,电阻率为30 Ω·m。该模型的构造特征主要是深部坳陷和隆起,其电阻率达10000 Ω·m。
|
图 9 复杂模型示意图(据文献[27]修改) |
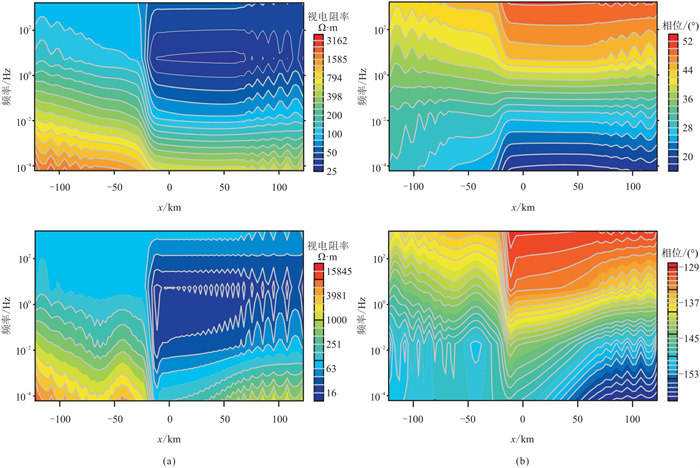
图 10为图 9模型TE模式和TM模式正演视电阻率和相位剖面,该剖面直观地反映了坳陷和隆起的分布。
|
图 10 复杂模型TE模式(上)和TM模式(下)下的正演视电阻率(a)和相位(b)剖面 |
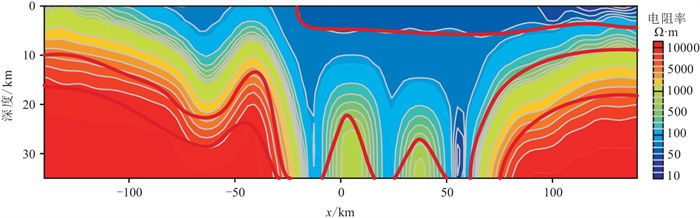
基于图 10正演数据开展快速一维反演,可获得针对性样本模型,再进行正演,获得针对性样本数据集,连同标准的样本数据集一起输入残差网络进行训练,然后对复杂模型视电阻率和相位数据集进行反演,电阻率反演结果见图 11,其残差网络反演均方误差为0.544546。对比图 11与图 9可见,对于复杂模型,基于残差网络可以很好地还原地下的凹陷与隆起。
|
图 11 复杂模型残差网络电阻率反演剖面 |
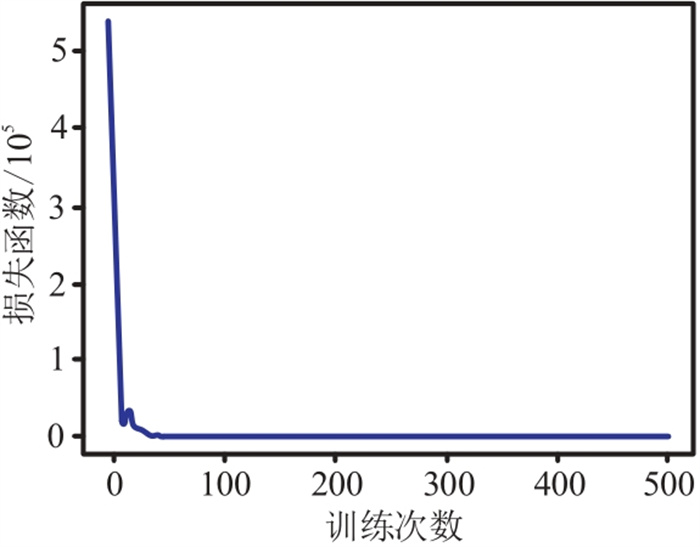
图 9所示模型的反演损失函数曲线见图 12。对比图 12与图 7可以看出:模型的复杂程度对于损失函数的训练会产生一定影响,通常情况下模型越复杂,损失函数收敛越慢,并出现局部震荡现象;随着训练次数的增加,损失函数会趋于一个平稳的极小值。
|
图 12 复杂模型残差网络反演损失函数曲线 |
实测数据来源于冀中坳陷深部碳酸盐岩热储调查项目。采用加拿大凤凰公司生产的V5-2000大地电磁测深仪开展数据采集,观测方式为“+”字形布极,电极距为50 m。勘探测线为1条,共53个测点,测点间距约1500 m,采集60个频点,频率范围为1.0×10-4 ~4.3×102 Hz。
根据研究区域已有的地质资料和岩石矿物测定结果,结合一维快速反演结果,加入比较符合该地区地电特征的数据集模型,将生成的样本数据集与标准数据集输入搭建的残差网络进行训练。
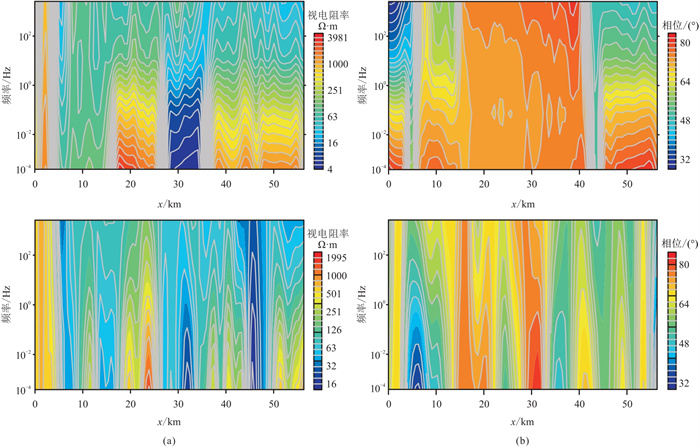
图 13为实测数据TE模式和TM模式下的视电阻率和相位剖面,可以大致反映地下电阻率分布特征。将该地区实测TE模式和TM模式下的视电阻率和相位数据输入训练好的残差网络,电阻率反演、解释结果见图 14。
|
图 13 实测数据TE模式(上)和TM模式(下)下的实测视电阻率(a)和相位(b)剖面 |
|
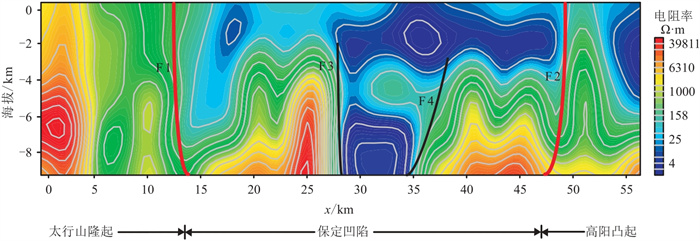
图 14 冀中坳陷实测数据电阻率反演及解释剖面F1~F4表示断裂。 |
根据解释结果,剖面上整体呈现“两凸一凹”的复杂结构,各构造单元分界线十分明显。根据大地电磁电阻率反演结果可以直观地判断热储能源的构造及分布,为地热勘探提供可靠的解释依据。
4 结论(1) 基于ResNet-18的大地电磁反演网络稳定性强,能够较准确地反演地下电性异常体的分布,不会因为网络层数过多引起准确度下降,体现了残差神经网络的优势。
(2) 模型反演中加入了不同程度的噪声,其反演结果都能很好地反映异常体形态和位置,表明残差神经网络有很好的抗噪能力。
(3) 将该方法成功应用于冀中坳陷热储能源构造研究,为该地区地热勘探和开发提供了有力的技术支撑。
| [1] |
邓琰, 汤吉, 阮帅. 三维大地电磁自适应正则化有限内存拟牛顿反演[J]. 地球物理学报, 2019, 62(9): 3601-3614. DENG Yan, TANG Ji, RUAN Shuai. Adaptive regularized three-dimensional magnetotelluric inversion based on the LBFGS quasi-Newton method[J]. Chinese Journal of Geophysics, 2019, 62(9): 3601-3614. |
| [2] |
王明亮, 张扬, 徐顺强, 等. 华北坳陷中南部深部结构大地电磁探测[J]. 地震地质, 2023, 45(2): 536-552. WANG Mingliang, ZHANG Yang, XU Shunqiang, et al. Deep structure in the middle and south area of North China depression and the vicinity by magnetotellurics[J]. Seismology and Geology, 2023, 45(2): 536-552. |
| [3] |
薛东旭, 刘诚, 郭发, 等. 基于土壤氡气测量和可控源音频大地电磁的陕西眉县汤峪地热预测[J]. 物探与化探, 2023, 47(5): 1169-1178. XUE Dongxu, LIU Cheng, GUO Fa, et al. Predicting the geothermal resources of the Tangyu geothermal field in Meixian County, Shaanxi Province, based on soil Radon measurement and the controlled source audio magnetotelluric method[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1169-1178. |
| [4] |
邵炳松, 石峰, 刘志龙, 等. 大地电磁测深法在太康隆起西部地热资源勘查中的应用研究[J]. 物探化探计算技术, 2023, 45(3): 379-388. SHAO Bingsong, SHI Feng, LIU Zhilong, et al. Application of the magnetotelluric sounding method in the exploration of geothermal resources in the West of the Taikang uplift[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2023, 45(3): 379-388. |
| [5] |
陈曦, 余小君, 胡德强. 大地电磁测深法在武定县罗能地热勘查中的应用[J]. 云南地质, 2018, 37(3): 343-348. CHEN Xi, YU Xiaojun, HU Deqiang. The application of terrestrial electromagnetic sounding to Luoneng geothermal exploration, Wuding[J]. Yunnan Geology, 2018, 37(3): 343-348. |
| [6] |
MACKIE R L, MADDEN T R. Three-dimensional magnetotelluric inversion using conjugate gradients[J]. Geophysical Journal International, 1993, 115(1): 215-229. |
| [7] |
CONSTABLE S C, PARKER R L, CONSTABLE C G. Occam’s inversion: a practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300. |
| [8] |
王鹤, 蒋欢, 王亮, 等. 大地电磁人工神经网络反演[J]. 中南大学学报(自然科学版), 2015(5): 1707-1714. WANG He, JIANG Huan, WANG Liang, et al. Magnetotelluric inversion using artificial neural network[J]. Journal of Central South University(Science and Technology), 2015(5): 1707-1714. |
| [9] |
MOGHADAS D. One-dimensional deep learning inversion of electromagnetic induction data using convolutional neural network[J]. Geophysical Journal International, 2020, 222(1): 247-259. |
| [10] |
廖晓龙, 张志厚, 姚禹, 等. 基于卷积神经网络的大地电磁反演[J]. 中南大学学报(自然科学版), 2020, 51(9): 2546-2557. LIAO Xiaolong, ZHANG Zhihou, YAO Yu, et al. Magnetotelluric inversion based on convolutional neural network[J]. Journal of Central South University(Science and Technology), 2020, 51(9): 2546-2557. |
| [11] |
李赓, 曹飞翔. 基于深度学习的二维航空大地电磁数据反演[J]. 科学技术与工程, 2021, 21(4): 1272-1278. LI Geng, CAO Feixiang. Inversion of two-dimensional airborne magnetotelluric data by deep learning[J]. Science Technology and Engineering, 2021, 21(4): 1272-1278. |
| [12] |
刘高村, 王绪本, 袁崇鑫, 等. Transformer网络在大地电磁反演成像中的应用[J]. 物探化探计算技术, 2023, 45(4): 484-496. LIU Gaocun, WANG Xuben, YUAN Chongxin, et al. Application of Transformer network in magnetotelluric inversion imaging[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2023, 45(4): 484-496. |
| [13] |
凌宏. 基于深度强化学习的大地电磁数据反演研究[D]. 吉林长春: 吉林大学, 2023. LING Hong. Research on Magnetotelluric Data Inversion Based on Deep Reinforcement Learning[D]. Jilin University, Changchun, Jilin, 2023. |
| [14] |
王斯昊, 何兰芳, 李亮. 神经网络在勘探地球物理的应用[J]. 新疆地质, 2022, 40(1): 73-77. WANG Sihao, HE Lanfang, LI Liang. Application of neural network in exploration geophysics[J]. Geology of Xinjiang, 2022, 40(1): 73-77. |
| [15] |
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, 770-778.
|
| [16] |
LIU Z, CHEN H, REN Z, et al. Deep learning audio magnetotellurics inversion using residual-based deep convolution neural network[J]. Journal of Applied Geophysics, 2021, 188: 104309. |
| [17] |
李梦迪. 基于深度学习的大地电磁反演研究[D]. 湖北荆州: 长江大学, 2023. LI Mengdi. Research on Magnetotelluric Inversion Based on Deep Learning[D]. Yangtze University, Jingzhou, Hubei, 2023. |
| [18] |
GUO R, YAO H, LI M, et al. Joint inversion of Audio-Magnetotelluric and seismic travel time data with deep learning constraint[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(9): 7982-7995. |
| [19] |
SONG T, SONG Y, WANG Y, et al. Residual network with dense block[J]. Journal of Electronic Imaging, 2018, 27(5): 53036.1-53036.9. |
| [20] |
HE K, ZHANG X, REN S, et al. Identity mappings in deep residual networks[M]//LEIBE B, MATAS J, SEBE N, et al. Computer Vision – ECCV 2016. Lecture Notes in Computer Science, Springer, Cham, 2016, 630-645.
|
| [21] |
ALBAWI S, MOHAMMED T A, AL-ZAWI S. Understanding of a convolutional neural network[C]. 2017 International Conference on Engineering and Technology(ICET), 2017, 1-6.
|
| [22] |
NWANKPA C, IJOMAH W, GACHAGAN A, et al. Activation functions: Comparison of trends in practice and research for deep learning[DB/OL]. (2018-11-08)[2024-03-15]. http://export.arxiv.org/abs/1811.03378.
|
| [23] |
SHAFIQ M, GU Z. Deep residual learning for image recognition: a survey[J]. Applied Sciences, 2022, 12(18): 8972. |
| [24] |
ABOSAMRA G, OQAIBI H. An optimized deep residual network with a depth concatenated block for handwritten characters classification[J]. Computers, Materials & Continua, 2021, 68(1): 1-28. |
| [25] |
DOGAN Y. A new global pooling method for deep neural networks: global average of Top-K Max-Pooling[J]. Traitement du Signal, 2023, 40(2): 577-587. |
| [26] |
CHAI T, ROLAND R R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature[J]. Geoscientific Model Development, 2014, 7(3): 1247-1250. |
| [27] |
苗青壮, 王贵玲, 邢林啸, 等. 综合物化探方法在冀中坳陷深部热储探测中的应用[J]. 地质学报, 2020, 94(7): 2147-2156. MIAO Qingzhuang, WANG Guiling, XING Linxiao, et al. Study on application of deep thermal reservoir by using geophysical and geochemical methods in the Jizhong depression zone[J]. Acta Geologica Sinica, 2020, 94(7): 2147-2156. |



 王大勇, 河北省廊坊市金光道84号中国地质科学院地球物理地球化学勘查研究所,065000。Email:
王大勇, 河北省廊坊市金光道84号中国地质科学院地球物理地球化学勘查研究所,065000。Email: