0 引言

地下深层地层压力是影响岩石性质的重要因素，准确预测地层压力对保证钻井安全、防止钻井事故具有重要意义^[1]，因此钻前地层压力预测越来越受到人们的重视。在复杂油气藏开发过程中，水力压裂是提高油气采收率的核心技术，可以增加非常规油气藏的渗透性，有效压力预测能够指导水力压裂方向设计，对提高油气产能具有重要意义。岩石物理理论表明，有效压力是岩石孔隙结构和流体性质的函数，因此，通过岩石物理模型构建有效压力和岩石弹性、物性特征的关系是合理预测有效压力的基础。

有效压力预测的基本理论是有效压力定律^[2-3]，该理论表明岩石孔隙和岩石骨架共同承担上覆岩石压力，因此分别求取垂直上覆压力和孔隙压力是估计有效压力的第一种方法。由不同深度的密度积分得到垂直上覆压力；计算孔隙压力一般需要获得地层的正常压实趋势，Eaton法是目前最常用的孔隙压力预测方法，该方法结合压实理论和异常高压成因机理，通过建立实测压力和测井信息之间的关系模型预测地层压力^[4]。然而，常规的利用声波时差拟合的正常压实趋势曲线的精度较低，导致地层压力预测精度较低。Fillippone公式不依赖于正常压实趋势线，通过地震速度直接计算地层压力，是估算较大范围地层压力的有效工具^[5]。估算有效压力的另一种方法是通过岩石物理手段建立储层特征或速度与有效压力的关系。人们进行了大量实验模拟深层储层的压力条件，并提出了压力与纵、横波速度之间的一些经验关系式^[6-7]。Han等^[8]对75块砂泥岩样本的测试结果表明，影响岩石速度的主要因素为孔隙度、泥质含量及垂直有效压力。基于上述理论，Eberhart-Phillips等^[9]提出了不同成因的异常压力砂泥岩地层的E-P经验模型，该模型的有效压力预测精度高于依赖于正常压实趋势线的方法。上述岩石物理方法仅停留在实验阶段或依赖经验模型，在理论上无法准确预测有效压力。

在岩石物理理论方面，多孔介质可压缩性的定义和有效压力概念的建立为考虑压力因素的岩石物理建模奠定了理论基础。Crampin等^[10]首先以易受有效压力影响的柔性孔隙纵横比为突破口，模拟了各向同性介质中随机定向柔性孔隙的压力敏感性。Hudson^[11]进一步扩展了这一想法，推导了有效压力与孔隙纵横比的变化关系，在超压页岩储层地震岩石物理建模中的应用效果较好。此外，Toksöz包裹体理论^[12]给出有效压力与裂缝体积变化率的关系。根据Hudson模型对裂缝体积的定义，可推导有效压力与裂缝纵横比的关系^[13]。近年来，孔隙空间刚度理论的提出为考虑压力因素的岩石物理建模提供了新思路^[14]。该理论在岩石可压缩性的研究基础上，描述了孔隙可压缩性与有效压力之间的关系，并用于计算饱和岩石体积模量^[15]。基于上述理论，刘仕友等^[16]构建了考虑有效压力因素的高压背景砂岩岩石物理模型。上述有效压力研究仅停留在岩石物理建模阶段，缺少由地震资料直接稳定预测有效压力的手段。

叠前地震反演技术利用地震波反射振幅随入射角或炮检距变化(AVA/AVO)的特征，是油气藏定量表征的重要技术和研究热点^[17]，因此另一种预测有效压力的思路应运而生，即从地震岩石物理理论出发，推导由有效压力直接表征的反射系数近似方程预测有效压力。上述储层参数反演方法一般分为两个步骤：第一步是将叠前地震数据转换为弹性参数；第二步是利用构建的理论或岩石物理经验模型，由弹性参数预测储层参数。因此，储层参数反演的质量不仅取决于弹性参数预测精度，还取决于岩石物理模型与真实岩石的匹配程度。此外，建立物性参数与弹性阻抗的岩石物理关系可以稳定预测孔隙结构等参数。

本文基于孔隙空间刚度理论及岩石弹性模量间的近似关系，建立了由剪切模量独立表征的有效压力岩石物理方程，并采用泰勒展开方法简化了方程的非线性性质^[18]。将推导的方程代入Russell方程，得到由有效压力直接表征的线性PP波反射系数方程。利用模型数据与实际资料测试了所提方法的有效压力预测效果。

1 与压力相关的岩石物理特征

为了描述岩石弹性模量与孔隙空间的关系，Mavko等^[14]基于Betti-Rayleigh互易定理^[19]，研究了具有任意孔隙度和孔隙空间弹性岩石的可压缩性。对于具有恒定孔隙压力的干岩石，有

$ \frac{1}{{K}_{\mathrm{d}}}=\frac{1}{{K}_{\mathrm{m}}}+\frac{ϕ }{{K}_{ϕ }} $

(1)

式中：$ {K}_{\mathrm{d}} $为干岩石体积模量；$ {K}_{\mathrm{m}} $为岩石基质体积模量；$ ϕ $为孔隙度；$ {K}_{ϕ } $为孔隙空间刚度，$ {K}_{ϕ }^{-1} $称为干岩石孔隙空间可压缩性。

实际数据分析表明，在孔隙连通性较好的情况下，$ k={K}_{ϕ }/{K}_{\mathrm{m}} $与有效压力$ {P}_{\mathrm{e}} $存在对数关系^[15]

$ k=A+B\mathrm{l}\mathrm{n}{P}_{\mathrm{e}} $

(2)

式中$ A $、$ B $均为常数，与地层的固有特征相关。

根据颗粒接触理论，$ {K}_{\mathrm{d}} $与干岩石剪切模量$ {\mu }_{\mathrm{d}} $均为$ ϕ $的简单函数，且$ {K}_{\mathrm{d}} $/$ {\mu }_{\mathrm{d}} $为0.667~1.667。对于砂岩储层，$ {K}_{\mathrm{d}} $/$ {\mu }_{\mathrm{d}} $约为0.9，且与$ ϕ $无关^[20]。基于以上研究，可以建立$ {\mu }_{\mathrm{d}} $和$ {K}_{\mathrm{d}} $的线性关系式^[16]

$ {\mu }_{\mathrm{d}}=\frac{{\mu }_{\mathrm{m}}{K}_{\mathrm{d}}}{c{K}_{\mathrm{m}}} $

(3)

式中：$ {\mu }_{\mathrm{m}} $为岩石基质剪切模量；$ c $为常数。

结合式(1)~式(3)，得到$ {\mu }_{\mathrm{d}} $随$ {P}_{\mathrm{e}} $变化的关系式

$ {\mu }_{\mathrm{d}}=\frac{{\mu }_{\mathrm{m}}}{c}{\left(1+\frac{ϕ }{A+B\mathrm{l}\mathrm{n}{P}_{\mathrm{e}}}\right)}^{-1} $

(4)

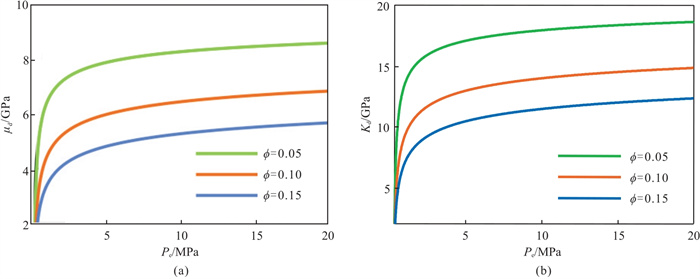
为了研究压力等参数对高压背景砂岩储层的影响，采用表 1数据模拟$ {\mu }_{\mathrm{d}} $和$ {K}_{\mathrm{d}} $随$ {P}_{\mathrm{e}} $的变化(图 1)，可见干岩石$ {\mu }_{\mathrm{d}} $与$ {P}_{\mathrm{e}} $、K_d与P_e均呈对数关系。

上述基于孔隙空间刚度理论的岩石物理分析仅停留在干岩石层面，对于孔隙空间内流体的研究同样重要。在声阻抗已知的情况下，Russell等^[21]提出了Gassmann流体因子f的概念^[22]

$ f=\frac{{\left(1-\frac{{K}_{d}}{{K}_{m}}\right)}^{2}{K}_{\mathrm{f}}}{ϕ +\left(\frac{1-ϕ }{{K}_{m}}-\frac{{K}_{d}}{{K}_{m}^{2}}\right){K}_{\mathrm{f}}} $

(5)

式中$ {K}_{\mathrm{s}} $为饱和岩石的体积模量。由于$ {K}_{\mathrm{m}} $远大于$ {K}_{\mathrm{f}} $，因此$ \left[\right(1-ϕ )/{K}_{\mathrm{m}}-{K}_{\mathrm{d}}/{K}_{\mathrm{m}}^{2}]{K}_{\mathrm{f}} $经常被舍去，故f可简化为

$ f={\left(1-\frac{{K}_{d}}{{K}_{m}}\right)}^{2}{ϕ }^{-1}{K}_{\mathrm{f}} $

(6)

根据式（4），f可进一步表示为$ {P}_{\mathrm{e}} $的函数

$ f={\left(\frac{ϕ }{A+B\mathrm{l}\mathrm{n}{P}_{\mathrm{e}}+ϕ }\right)}^{2}\frac{{K}_{\mathrm{f}}}{ϕ } $

(7)

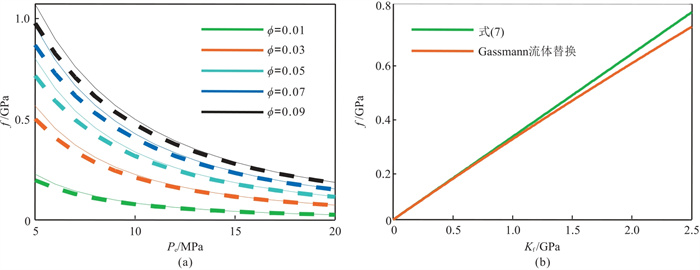
为了验证式(7)的精度，采用表 1数据将式(7)与Gassmann流体替换结果对比。图 2为在不同$ ϕ $时式(7)与Gassmann流体替换结果对比。由图可见：①$ {P}_{\mathrm{e}} $与f呈反比，且式(7)与流体替换结果吻合良好，验证了简化过程的合理性(图 2a)。但需要注意的是，当$ {P}_{\mathrm{e}} $趋近于零时，f对$ ϕ $的变化不明显，这也造成式(7)与式(5)的交叉现象。②式(7)与式(5)之间的差别随着$ {K}_{\mathrm{f}} $的增加而不断增大，但两者总体趋于一致，符合储层预测的精度要求(图 2b)。

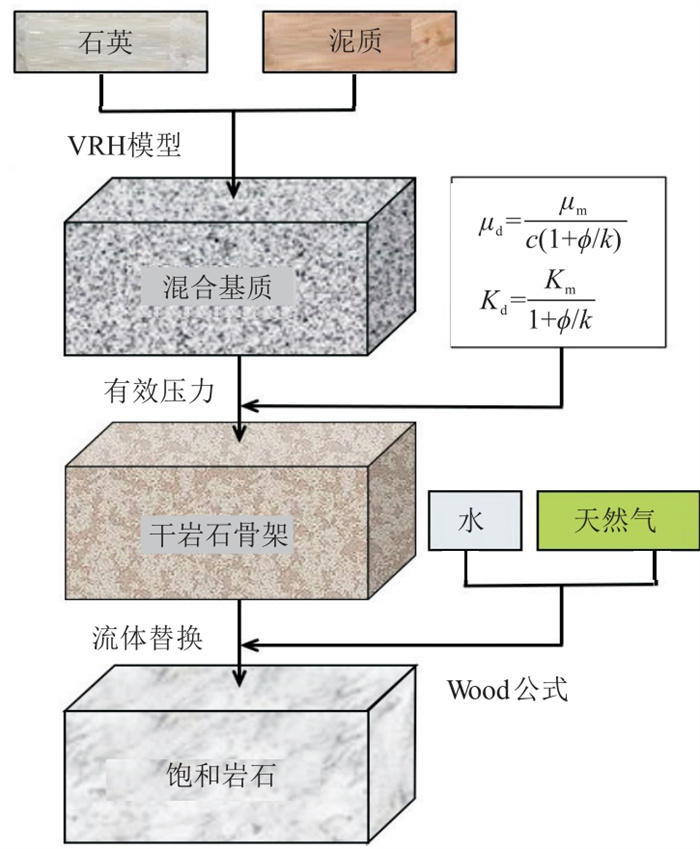
在实际工作中，参数A、B往往难以选择。为此，提出了基于纵横波约束的A、B分步预测算法。首先采用V-R-H模型^[23]求取混合基质的弹性模量；随后向岩石基质中添加$ {P}_{\mathrm{e}} $的影响得到干岩石骨架；最后利用Wood公式^[24]求取混合流体的弹性模量并进行流体替换。最终建立了相应的岩石物理模型(图 3)。

由于组成岩石的矿物成分复杂，因此估算矿物弹性模量及参数A、B为多元函数求解问题。设通过岩石物理模型计算岩石纵、横波速度的函数为$ {F}_{1} $、$ {F}_{2} $，即

$ \begin{array}{l}{F}_{1}\left(\right[{\rho }_{i}, {V}_{\mathrm{泥}{\mathrm{质}}_{i}}, {V}_{\mathrm{石}{\mathrm{英}}_{i}}, {K}_{\mathrm{泥}\mathrm{质}}, {K}_{\mathrm{石}\mathrm{英}}, \\ {U}_{\mathrm{泥}\mathrm{质}}, {U}_{\mathrm{石}\mathrm{英}}, {ϕ }_{i}, {S}_{{\mathrm{w}}_{i}}, A, B\left]\right)={v}_{\mathrm{P}i}^{\mathrm{c}\mathrm{a}\mathrm{l}}\end{array} $

(8)

$ \begin{array}{l}{F}_{2}\left(\right[{\rho }_{i}, {V}_{\mathrm{泥}{\mathrm{质}}_{i}}, {V}_{\mathrm{石}{\mathrm{英}}_{i}}, {U}_{\mathrm{泥}\mathrm{质}}, {U}_{\mathrm{石}\mathrm{英}}, \\ {ϕ }_{i}, {S}_{{\mathrm{w}}_{i}}, A, B\left]\right)={v}_{\mathrm{S}i}^{\mathrm{c}\mathrm{a}\mathrm{l}}\end{array} $

(9)

式中；$ \rho $为密度；$ {V}_{\mathrm{泥}\mathrm{质}i} $和$ {V}_{\mathrm{石}\mathrm{英}i} $分别为泥质和石英的体积分数，下标$ i $表示第$ i $个采样点；$ {K}_{\mathrm{泥}\mathrm{质}} $和$ {K}_{\mathrm{石}\mathrm{英}} $分别为泥质和石英的体积模量；$ {U}_{\mathrm{泥}\mathrm{质}} $和$ {U}_{\mathrm{石}\mathrm{英}} $分别为泥质和石英的剪切模量；$ {S}_{\mathrm{w}i} $为含水饱和度；$ {v}_{\mathrm{P}i}^{\mathrm{c}\mathrm{a}\mathrm{l}} $为预测纵波速度；$ {v}_{\mathrm{S}i}^{\mathrm{c}\mathrm{a}\mathrm{l}} $为预测横波速度。

由于实际测井数据的采样点较密集(一般采样间距为0.125 m)，因此求解该多元函数为超定问题，具体的计算流程如下。

(1) 给定岩石各组分矿物剪切模量、体积模量及参数A、B的取值范围。

(2) 以实测横波速度为约束，在取值范围内寻找基质矿物的剪切模量。定义目标函数为

$ {\psi }_{1}=\sum\limits_{i=1}^{M}\left|{v}_{\mathrm{S}i}-{v}_{\mathrm{S}\mathrm{i}}^{\mathrm{c}\mathrm{a}\mathrm{l}}\right| $

(10)

式中：M为总采样点数；$ {v}_{\mathrm{S}i} $为第$ i $个采样点的实测横波速度。当目标函数最小时，则认为取得基质矿物剪切模量及参数A、B的最优解。

(3) 利用上一步得到的各矿物剪切模量及参数A、B，以实测纵波速度$ {v}_{\mathrm{P}i} $为约束，在取值范围内寻找各矿物的体积模量。定义目标函数为

$ {\psi }_{2}=\sum\limits_{i=1}^{M}\left|{v}_{\mathrm{P}i}-{v}_{\mathrm{P}\mathrm{i}}^{\mathrm{c}\mathrm{a}\mathrm{l}}\right| $

(11)

当目标函数最小时，则认为取得基质矿物体积模量的最优解。

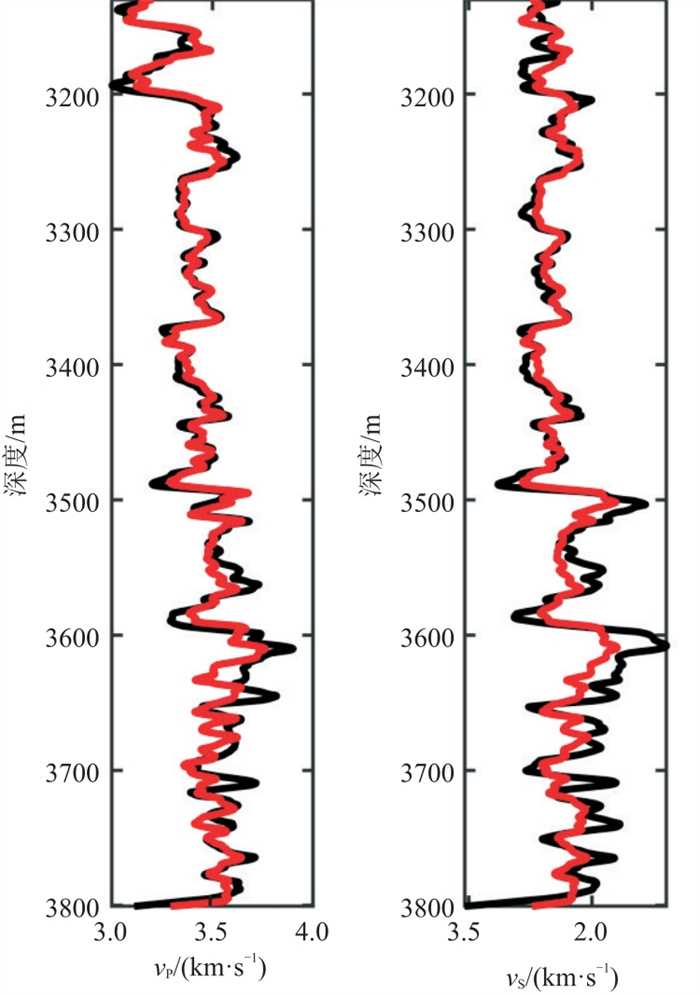
利用上述算法得到基质矿物剪切模量、体积模量及参数A、B的预测结果(表 2)。将上述参数代入砂岩储层岩石物理模型，得到速度预测结果(图 4)。可见，预测速度与实测速度变化趋势相同、数值相近，表明A、B预测值的精度较高，为岩石物理分析及反演提供了基础。

2 新反射系数方程及反演目标函数构建 2.1 由P_e表征的反射系数方程

基于Biot-Gassmann孔隙弹性理论^[2-3]，Russell等^[21]推导了关于$ f $、$ {\mu }_{\mathrm{d}} $和$ \rho $的线性化PP波反射系数方程

$ \begin{array}{l}{R}_{\mathrm{P}\mathrm{P}}\left(\theta \right)={a}_{f}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{\mathrm{\Delta }f}{\stackrel{-}{f}}+{a}_{{\mu }_{\mathrm{d}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{\mathrm{\Delta }\mu }{\stackrel{-}{\mu }}+\\ {a}_{\rho }^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{\mathrm{\Delta }\rho }{\stackrel{-}{\rho }}\end{array} $

(12)

其中

$ \left\{\begin{array}{l}{a}_{f}^{\mathrm{P}\mathrm{P}}\left(\theta \right)=\left(1-\frac{{\gamma }_{\mathrm{d}}^{2}}{{\gamma }_{\mathrm{s}}^{2}}\right)\frac{\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{4}\\ {a}_{{\mu }_{\mathrm{d}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)=\frac{{\gamma }_{\mathrm{d}}^{2}}{4{\gamma }_{\mathrm{s}}^{2}}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -\frac{2}{{\gamma }_{\mathrm{s}}^{2}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \\ {a}_{\rho }^{\mathrm{P}\mathrm{P}}\left(\theta \right)=\frac{1}{2}-\frac{\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{4}\end{array}\right. $

(13)

式中：$ \theta $为入射角；$ {\gamma }_{\mathrm{d}}^{2} $为干岩石纵横波速度比的平方；$ {\gamma }_{\mathrm{s}}^{2} $为饱和岩石纵横波速度比的平方；$ \mathrm{\Delta } $(•)、($ \overline{•} $)分别为上、下层介质物理量的差值与平均值(下同)。

由于$ f $为$ {K}_{\mathrm{f}} $、$ ϕ $和P_e的函数，$ {\mu }_{\mathrm{d}} $为$ {\mu }_{\mathrm{m}} $、$ ϕ $和P_e的函数。因此，对式(12)的$ f $和$ {\mu }_{\mathrm{d}} $项进行泰勒展开^[18]，得到$ f $和$ {\mu }_{\mathrm{d}} $的反射率

$ \left\{\begin{array}{l}\frac{\mathrm{\Delta }f}{f}\approx \frac{\mathrm{\Delta }{K}_{\mathrm{f}}}{{\overline{K}}_{\mathrm{f}}}+\frac{k-ϕ }{k+ϕ }\frac{\mathrm{\Delta }ϕ }{\overline{ϕ }}-\frac{2B}{k+ϕ }\frac{\mathrm{\Delta }{P}_{\mathrm{e}}}{{\stackrel{-}{P}}_{\mathrm{e}}}\\ \frac{\mathrm{\Delta }{\mu }_{\mathrm{d}}}{{\mu }_{\mathrm{d}}}\approx \frac{\mathrm{\Delta }{\mu }_{\mathrm{m}}}{{\overline{\mu }}_{\mathrm{m}}}-\frac{ϕ }{k+ϕ }\frac{\mathrm{\Delta }ϕ }{\overline{ϕ }}+\frac{Bϕ }{k(k+ϕ )}\frac{\mathrm{\Delta }{P}_{\mathrm{e}}}{{\stackrel{-}{P}}_{\mathrm{e}}}\end{array}\right. $

(14)

将式(14)代入Russell方程即可得到关于$ {K}_{\mathrm{f}} $、P_e、$ ϕ $、$ {\mu }_{\mathrm{m}} $和$ \rho $的新反射系数方程$ \begin{array}{l}{R}_{\mathrm{P}\mathrm{P}}={a}_{{K}_{\mathrm{f}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{\mathrm{\Delta }{K}_{\mathrm{f}}}{\stackrel{-}{K}{}_{\mathrm{f}}}+{a}_{{P}_{\mathrm{e}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{\mathrm{\Delta }{P}_{\mathrm{e}}}{{\stackrel{-}{P}}_{\mathrm{e}}}+\\ {a}_{ϕ }^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{\mathrm{\Delta }ϕ }{\stackrel{-}{ϕ }}+{a}_{{\mu }_{\mathrm{m}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{\mathrm{\Delta }{\mu }_{\mathrm{m}}}{{\stackrel{-}{\mu }}_{\mathrm{m}}}+{a}_{\rho }^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{\mathrm{\Delta }\rho }{\stackrel{-}{\rho }}\end{array} $(15)

其中

$ \left\{\begin{array}{l}{a}_{{K}_{\mathrm{f}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)={a}_{f}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\\ {a}_{{P}_{\mathrm{e}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)=-{a}_{f}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{2B}{k+ϕ }+{a}_{{\mu }_{\mathrm{d}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{Bϕ }{k(k+ϕ )}\\ {a}_{ϕ }^{\mathrm{P}\mathrm{P}}\left(\theta \right)={a}_{f}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{k-ϕ }{k+ϕ }-{a}_{{\mu }_{\mathrm{d}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\frac{ϕ }{k+ϕ }\\ {a}_{{\mu }_{\mathrm{m}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)={a}_{{\mu }_{\mathrm{d}}}^{\mathrm{P}\mathrm{P}}\left(\theta \right)\end{array}\right. $

(16)

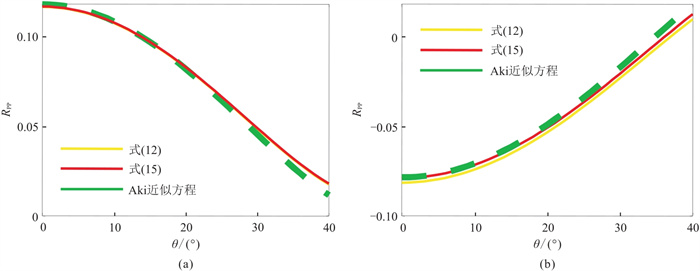
为了验证式(15)的精度，设计了三层含气砂岩模型(表 3)。图 5为式(12)、式(15)与Aki近似方程^[25]的R_PP对比。由图可见：①当θ < 30°时，三式的R_PP一致性较好，证明式(15)的精度较高；②当θ≥30°时，三式的R_PP偏离程度逐渐增大，这是因为在式(15)推导过程中采用了泰勒展开，因此降低了精度。

2.2 反演目标函数构建

根据褶积模型，将式（15）改为矩阵形式

$ \boldsymbol{R}=\boldsymbol{Am} $

(17)

式中：$ \boldsymbol{A} $为系数矩阵；$ \boldsymbol{m} $为待反演参数矩阵。

假设存在W个入射角，式(17)可以表示为

$ \left[\begin{array}{c}{R}_{\mathrm{P}\mathrm{P}}\left({\theta }_{1}\right)\\ {R}_{\mathrm{P}\mathrm{P}}\left({\theta }_{2}\right)\\ ⋮\\ {R}_{\mathrm{P}\mathrm{P}}\left({\theta }_{W}\right)\end{array}\right]=\left[\begin{array}{ccccc}{a}_{{K}_{\mathrm{f}}}\left({\theta }_{1}\right)& {a}_{{P}_{\mathrm{e}}}\left({\theta }_{1}\right)& {a}_{ϕ }\left({\theta }_{1}\right)& {a}_{{\mu }_{\mathrm{m}}}\left({\theta }_{1}\right)& {a}_{\rho }\left({\theta }_{1}\right)\\ {a}_{{K}_{\mathrm{f}}}\left({\theta }_{2}\right)& {a}_{{P}_{\mathrm{e}}}\left({\theta }_{2}\right)& {a}_{ϕ }\left({\theta }_{2}\right)& {a}_{{\mu }_{\mathrm{m}}}\left({\theta }_{2}\right)& {a}_{\rho }\left({\theta }_{2}\right)\\ & & ⋮& & \\ {a}_{{K}_{\mathrm{f}}}\left({\theta }_{W}\right)& {a}_{{P}_{\mathrm{e}}}\left({\theta }_{W}\right)& {a}_{ϕ }\left({\theta }_{W}\right)& {a}_{{\mu }_{\mathrm{m}}}\left({\theta }_{W}\right)& {a}_{\rho }\left({\theta }_{W}\right)\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{K}_{\mathrm{f}}\\ \mathrm{\Delta }{P}_{\mathrm{e}}\\ \mathrm{\Delta }ϕ \\ \mathrm{\Delta }{\mu }_{\mathrm{m}}\\ \mathrm{\Delta }\rho \end{array}\right] $

(18)

地震褶积模型可以表示为

$ \boldsymbol{S}=\boldsymbol{gm} $

(19)

式中$ \boldsymbol{g} $为正演算子。

每个模型参数之间存在一定相关性，可以通过共轭梯度优化方法去相关处理。对式（19）去相关处理，得到正演算子$ \boldsymbol{G} $和模型参数矩阵$ \boldsymbol{M} $

$ \left\{\begin{array}{l}\boldsymbol{G}=\boldsymbol{gU}\\ \boldsymbol{M}=\boldsymbol{U}^{-1}\boldsymbol{m}\end{array}\right. $

(20)

式中$ \boldsymbol{U} $为模型参数反射系数协方差矩阵的特征向量。最终的褶积模型为

$ \boldsymbol{S}=\boldsymbol{GM} $

(21)

在贝叶斯反演框架中，通过模型参数和似然函数的先验概率分布预测模型参数的后验概率分布，文中主要采用柯西分布作为模型参数的先验概率分布。假设观测记录噪声服从高斯分布，则后验概率分布函数$ P $为

$ P\left(\boldsymbol{M}, {\sigma }_{\mathrm{n}}|\boldsymbol{S}\right)\propto \prod\limits_{j=1}^{N}\left[\frac{1}{\boldsymbol{I}+\boldsymbol{M}_{j}^{2}/{\sigma }_{\mathrm{m}}^{2}}\right]\cdot \\ \mathrm{e}\mathrm{x}\mathrm{p}\left[\frac{-{(\boldsymbol{S}-\boldsymbol{GM})}^{\mathrm{T}}(\boldsymbol{S}-\boldsymbol{GM})}{2{\sigma }_{\mathrm{n}}^{2}}\right] $

(22)

式中：$ N $为模型参数个数；$ \boldsymbol{I} $为单位矩阵；$ {\sigma }_{\mathrm{n}} $和$ {\sigma }_{\mathrm{m}} $分别为随机噪声和模型参数的标准差。

将式(22)代入边缘化公式^[26]，由最大化后验概率分布得到包含未知参数的目标函数

$ \begin{array}{l}F\left(\boldsymbol{M}\right)={(\boldsymbol{S}-\boldsymbol{GM})}^{\mathrm{T}}(\boldsymbol{S}-\boldsymbol{GM})+\\ 2{\sigma }_{\mathrm{n}}^{2}\sum\limits_{j=1}^{N}\mathrm{l}\mathrm{n}\left(\boldsymbol{I}+\frac{\boldsymbol{M}_{j}^{2}}{{\sigma }_{m}^{2}}\right)\end{array} $

(23)

由于地震数据中存在噪声以及缺乏低频信息，可能导致反演结果不稳定。建立良好的未知参数低频模型有助于提高反演结果稳定性和横向连续性。因此，在方程中引入平滑背景参数模型约束^[27]，则目标函数变为

$ F\text{'}\left(\boldsymbol{M}\right)=F\left(\boldsymbol{M}\right)+\boldsymbol{\varLambda } $

(24)

其中

$ \boldsymbol{\varLambda }=\sum\limits_{j=1}^{5}{\lambda }_{{\boldsymbol{M}}_{j}}{\left({\boldsymbol{\eta }}_{{\boldsymbol{M}}_{j}}-{\boldsymbol{P}}_{{\boldsymbol{M}}_{j}}{\boldsymbol{R}}_{{\boldsymbol{M}}_{j}}\right)}^{\mathrm{T}}\left({\boldsymbol{\eta }}_{{\boldsymbol{M}}_{j}}-{\boldsymbol{P}}_{{\boldsymbol{M}}_{j}}{\boldsymbol{R}}_{{\boldsymbol{M}}_{j}}\right) $

式中：$ {\lambda }_{{\boldsymbol{M}}_{j}} $为待反演参数的约束系数；$ {\boldsymbol{\eta }}_{{\boldsymbol{M}}_{j}}=0.5\mathrm{l}\mathrm{n}\left({\boldsymbol{M}}_{j}/{M}_{j}^{0}\right) $，$ {M}_{j}^{0} $为模型参数的初始值；P_Mj为道积分矩阵；$ {\boldsymbol{R}}_{{\boldsymbol{M}}_{j}} $为反射系数矩阵。

使目标函数最小并进行道积分，即可得到各参数的反演结果。

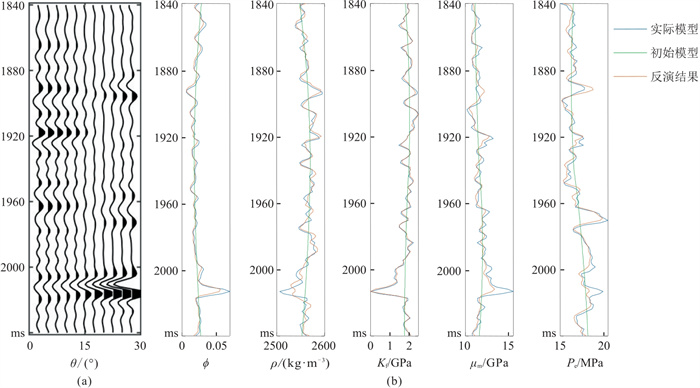
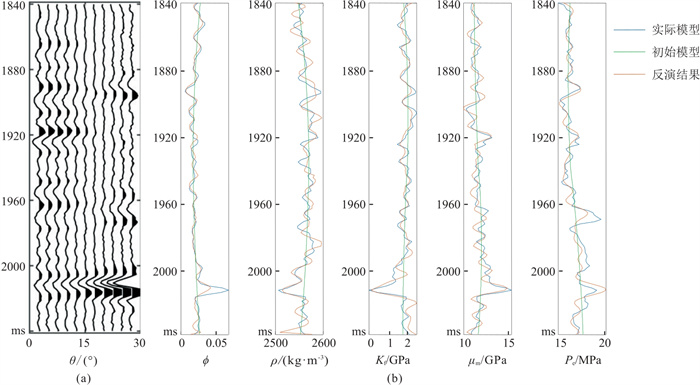
3 模型数据测试与实际资料应用 3.1 模型数据测试

以式(15)得到的R_PP与25 Hz的Ricker子波褶积合成角度域叠前角道集，合成地震道的入射角范围为0°~30°。图 6为无噪声模型测试结果。由图可见，在无噪情况下，ϕ、ρ、K_f、μ_m和P_e的反演结果与实际模型吻合较好，证明了所提反演方法的可行性。图 7为信噪比SNR=5的模型测试结果。由图可见，在加噪情况下，各模型参数的反演结果与实际模型的吻合度仍较高，验证了所提反演方法的稳定性。

3.2 实际资料应用

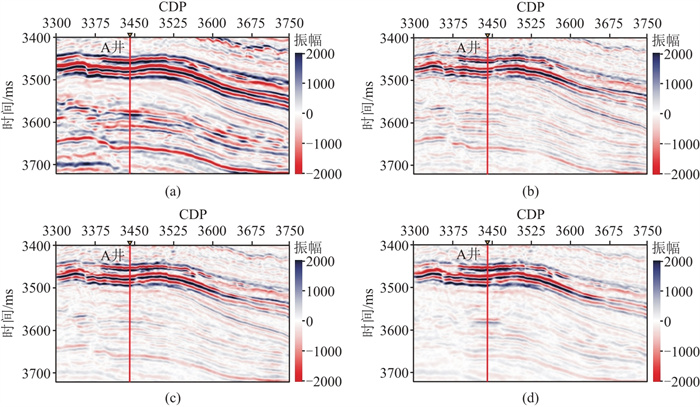
中国南部F区地层广泛呈现压力异常特征，且压力异常层段往往蕴含天然气。图 8为叠后和部分角度叠加地震数据。由图可见，天然气发育范围为3450~3485 ms。

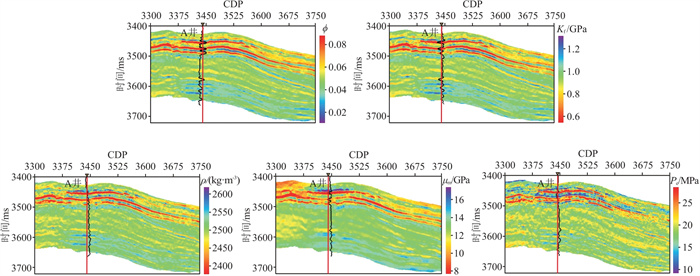
图 9为反演结果。由图可见，在天然气发育位置，K_f呈低值，ϕ和P_e则呈高值异常，ρ及μ_m无明显变化。总体而言，该反演结果可以识别储层内的含烃岩体，计算结果与实际测井数据一致，证明了所提方法对于实际资料的有效性和实用性。

4 结束语

本文综合孔隙空间刚度理论、流体替换方程等相关假设，推导了有效压力与岩石骨架剪切模量、Gassmann流体因子的函数表达式。岩石物理分析表明，有效压力与Gassmann流体因子呈反比，因此有效压力可指示孔隙度及孔隙流体的变化。此外，本文利用泰勒展开得到弹性参数与物性参数的线性转换关系，由此推导了由有效压力直接表征的反射系数方程, 奠定了反演有效压力的基础。在贝叶斯框架下，构建了平滑初始模型约束的叠前地震反演流程，提高了反演结果的稳定性。模型测试与实际资料应用表明，即使在低信噪比情况下，文中方法依然能稳定预测地层有效压力。