2. 青岛市水利勘测设计研究院有限公司, 山东青岛 266071
2. Qingdao Water Conservancy Survey & Design Research Institute Co., Ltd., Shandong, Qingdao 266071, China
在油气勘探、开发领域,弹性参数模型广泛应用于识别储层类型、预测储层性质以及评估储层质量和开发潜力[1-3]。但是,随着油气勘探、开发由浅部向深部[4]、由常规向特殊岩性油气藏的转移[5-6],研究目标的复杂程度和不确定性显著提升,难以建立可靠且满足分辨率要求的确定性弹性参数模型。相比于确定性建模,随机建模在构建复杂模型、高分辨率建模以及模型不确定性评价等方面具备显著优势。
随机建模方法的重要理论之一是地质统计学,包括克里金方法、随机模拟方法和多点地质统计学方法。随机模拟方法基于两点地质统计学克里金理论,利用变差函数表征空间相关性,主要包括序贯高斯模拟方法、序贯指示模拟方法和直接序贯模拟方法[7-8]。多点地质统计学方法使用训练图像代替变差函数描述空间相关关系,相较于随机模拟方法适用于构建更复杂的随机模型[9]。随机建模方法应用十分广泛,乐友喜等[10]利用基于序贯高斯模拟的速度场随机建模方法分析了油气储层构造图的不确定性;李祺鑫等[11]基于贝叶斯理论,将地震约束引入序贯高斯模拟,降低了随机模型的不确定性;Soares[12]提出直接序贯模拟和直接序贯协模拟方法,相比序贯高斯模拟方法极大提升了计算效率;刘兴业等[13]结合多点地质统计学、序贯高斯模拟方法和地震反演方法,构建了高分辨率的储层岩相和弹性参数随机模型。然而,由于变差函数无法描述复杂且非平稳的空间相关关系,随机模拟方法难以准确构建复杂模型,多点地质统计学方法的局限性则在于难以选取合适的训练图像[14]。
Ravalec等[15]提出了快速傅里叶滑动平均(FFT-MA)法。FFT-MA方法使用空间结构模型表征模型区域化变量的空间相关性,通过傅里叶变换将空间结构模型与随机数在频率域相结合,再通过傅里叶逆变换在空间域生成满足指定空间结构关系的随机模型。FFT-MA方法越来越多地被应用于建立高分辨率弹性参数模型,杨修伟等[16-17]提出了基于FFT-MA的随机介质建模方法,该方法适用于建立二维和三维的平稳及非平稳弹性参数随机模型,具有高效、灵活的优点;王保丽等[18]和孙瑞莹等[19]将FFT-MA方法引入地震随机反演得到保持空间结构特征的高分辨率弹性参数模型,并结合逐渐变形法使建模结果符合实际地震记录,提高了建模结果的准确性与稳定性。准确构建空间结构模型是利用FFT-MA方法生成合理的随机模型的关键,Yin等[20]通过变差结构分析得到的变差函数并建立空间结构模型,但无法描述非平稳的空间相关性特征;顾元等[21]基于地震褶积模型的功率谱法、使用叠后地震数据直接对结构参数进行求解从而建立空间结构模型。Irving等[22-24]建立了弹性参数模型与叠后地震数据的函数关系式,通过Monte Carlo方法反演结构参数,但是该方法的反演结果并不稳定。此外,仅基于地震数据估计空间结构模型没有整合测井的纵向高分辨率信息,建模结果的纵向分辨率较低。
本文提出了一种可靠的空间结构模型估计方法。该方法通过最小化随机模型与测井数据和地震数据的空间结构差异分别反演纵向自相关长度和横向自相关长度。为了提高纵向自相关长度的反演效果,引入边界保护正则化[25]以提高反演的稳定性。然后,利用反演得到的纵向自相关长度和横向自相关长度构建空间结构模型,并将其用于FFT-MA弹性参数随机建模。此外,为提高随机模型的稳定性,引入地震约束优选随机模型。最后,在实际资料测试中成功构建了复杂储层的弹性参数非平稳随机模型,验证了本文方法的正确性和有效性。
1 方法原理 1.1 FFT-MA随机建模方法FFT-MA是一种结合了快速傅里叶变换(FFT)和滑动平均法(MA)的随机建模方法。滑动平均法将均值为0、方差为1的高斯白噪w转化为同样均值为0、方差为1且满足空间自相关函数C的高斯随机场y。以二维建模为例,平稳假设下建模区域内的自相关函数不随位置变化,即
| $ C(x, t, \mathrm{\Delta }x, \mathrm{\Delta }t)={C}_{0}(\mathrm{\Delta }x, \mathrm{\Delta }t) $ | (1) |
式中:C0表示平稳自相关函数;Δx、Δt分别表示以(x,t)为原点的横、纵相对坐标。随机建模常用的自相关函数类型包括高斯型、指数型和混合型[26-27],本文使用指数型自相关函数
| $ \begin{array}{l}{C}_{0}(\mathrm{\Delta }x, \mathrm{\Delta }t)=\mathrm{e}\mathrm{x}\mathrm{p}\left\{-\left[\frac{{\left(\mathrm{\Delta }x\mathrm{c}\mathrm{o}\mathrm{s}\theta +\mathrm{\Delta }t\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)}^{2}}{{a}^{2}}+\right.\right.\\ \left.{\left.\begin{array}{cc}& \end{array}\frac{{\left(-\mathrm{\Delta }x\mathrm{s}\mathrm{i}\mathrm{n}\theta +\mathrm{\Delta }t\mathrm{c}\mathrm{o}\mathrm{s}\theta \right)}^{2}}{{b}^{2}}\right]}^{\frac{1}{2}}\right\}\end{array} $ | (2) |
式中:a、b分别为横向自相关长度和纵向自相关长度;θ为自相关角度。参数a、b和θ分别控制了自相关函数的水平、垂直相关性和旋转角度。此时,平稳FFT-MA高斯随机场可以表示为
| $ {y}_{0}(\mathrm{\Delta }x, \mathrm{\Delta }t)={g}_{0}(\mathrm{\Delta }x, \mathrm{\Delta }t)\mathrm{*}w(\mathrm{\Delta }x, \mathrm{\Delta }t) $ | (3) |
式中:*表示卷积运算;g0为C0的分解,即
| $ {C}_{0}(\mathrm{\Delta }x, \mathrm{\Delta }t)={g}_{0}(\mathrm{\Delta }x, \mathrm{\Delta }t)\mathrm{*}{g}_{0}(-\mathrm{\Delta }x, -\mathrm{\Delta }t) $ | (4) |
通常很难求解g0且结果不稳定。因此将傅里叶变换引入滑动平均法,在频率域求解。对式(3)做傅里叶变换,有
| $ {Y}_{0}({k}_{\mathrm{\Delta }x}, {f}_{\mathrm{\Delta }t})={G}_{0}({k}_{\mathrm{\Delta }x}, {f}_{\mathrm{\Delta }t})·W({k}_{\mathrm{\Delta }x}, {f}_{\mathrm{\Delta }t}) $ | (5) |
式中:Y0、G0、W分别为y0、g0和w的傅里叶谱;kΔx和fΔt分别为Δx和Δt对应的波数和频率。
根据维纳—辛钦定理,功率谱与自相关函数互为傅里叶变换对,因此式(4)转换至频率域为
| $ {S}_{0}({k}_{\mathrm{\Delta }x}, {f}_{\mathrm{\Delta }t})={G}_{0}({k}_{\mathrm{\Delta }x}, {f}_{\mathrm{\Delta }t})·{\tilde{G}}_{0}({k}_{\mathrm{\Delta }x}, {f}_{\mathrm{\Delta }t}) $ | (6) |
式中:S0为C0的功率谱;
| $ {G}_{0}({k}_{\mathrm{\Delta }x}, {f}_{\mathrm{\Delta }t})=\sqrt{{S}_{0}({k}_{\mathrm{\Delta }x}, {f}_{\mathrm{\Delta }t})} $ | (7) |
将式(7)代入式(5),并将计算结果做傅里叶逆变换,即可得到平稳FFT-MA高斯随机场y0。
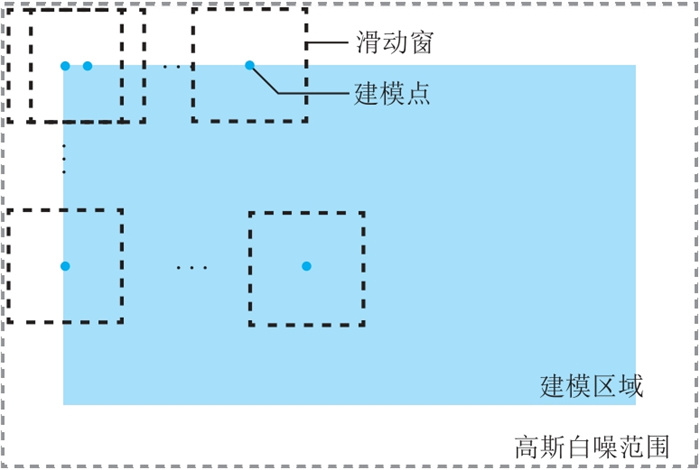
然而,地下介质的空间相关性往往是非平稳的,每一个建模点对应不同的自相关函数C,此时需要逐点构造非平稳FFT-MA高斯随机场y(x, t)。图 1为非平稳FFT-MA建模策略示意图,蓝色区域为建模区域,虚线矩形框为高斯白噪覆盖的范围,可见高斯白噪的范围要大于建模区域范围。对于每一个建模点
|
图 1 非平稳FFT-MA建模策略示意图 |
最后通过下式建立背景值为m0、扰动标准差为σm的随机模型m
| $ m(x, t)={m}_{0}(x, t)+{\sigma }_{\mathrm{m}}(x, t)y(x, t) $ | (8) |
m0描述了模型的大尺度非均匀性变化趋势,y描述了模型的小尺度非均匀性信息,σm用于调整y的扰动范围。
1.2 空间结构模型的估计利用FFT-MA方法生成合理的随机模型的关键在于构建准确的空间自相关函数C,即空间结构模型。为此,需要估计横向自相关长度a、纵向自相关长度b和角度参数θ。θ可根据叠后地震剖面揭示的地层倾角估计;a、b则分别基于地震数据和测井数据、通过反演估计。
将纵向自相关长度b的反演问题设置为最小化井旁道一维FFT-MA高斯随机场y(t) 的自相关函数与测井曲线高频成分L(t)自相关函数之间的差异。对于一维数组X,其自相关函数可表示为
| $ {C}_{\boldsymbol{X}}\left(\tau \right)=\frac{1}{N}\sum\limits_{i=1}^{N}\left(\frac{{X}_{i}-{\mu }_{\boldsymbol{X}}}{{\sigma }_{X}}\right)\left(\frac{{X}_{i+\tau }-{\mu }_{X}}{{\sigma }_{X}}\right) $ | (9) |
式中:τ为时差;N、μX、σX分别为X的样点数、均值和标准差。本文使用均方误差(MSE)衡量y(t)自相关与L(t)自相关之间的差异,即
| $ \mathrm{M}\mathrm{S}\mathrm{E}\left[{C}_{y}^{b}\left(\tau \right), {C}_{L}\left(\tau \right)\right]=\frac{1}{n}\sum\limits_{\tau =1}^{n}{\left[{C}_{y}^{b}\left(\tau \right)-{C}_{L}\left(\tau \right)\right]}^{2} $ | (10) |
式中:
通过调整b(t)减小式(10)中的MSE,能够减小y(t) 自相关函数与L(t)自相关函数之间的差异。为进一步提高b(t)的反演精度,提取y(t)和L(t)在不同深度的片段,构造反演目标函数
| $ {J}^{b}=\frac{1}{M}\sum\limits_{i=1}^{M}\mathrm{M}\mathrm{S}{\mathrm{E}}_{i}\left[{C}_{y}^{b}\left(\tau \right), {C}_{L}\left(\tau \right)\right] $ | (11) |
式中M为分段数量。
为进一步提高b(t)的反演稳定性,在反演过程中引入边界保护正则化,得到新的反演目标函数
| $ {J}^{b}=\frac{1}{M}\sum\limits_{i=1}^{M}\mathrm{M}\mathrm{S}{\mathrm{E}}_{i}\left[{C}_{y}^{b}\left(\tau \right), {C}_{L}\left(\tau \right)\right]+{R}^{b} $ | (12) |
式中Rb为梯度函数构成的非线性正则化项,可表示为
| $ {R}^{b}=\lambda \frac{{\left\{\frac{D\left[b\left(t\right)\right]}{\delta }\right\}}^{2}}{1+{\left\{\frac{D\left[b\left(t\right)\right]}{\delta }\right\}}^{2}} $ | (13) |
其中:D[b(t)]为b(t)对时间t的平均梯度;λ、δ分别为权重和尺度正则化参数。λ用于平衡目标函数中的数据项与正则化项;δ用于控制D[b(t)],从而控制b(t)反演结果的边界特性。
与估计纵向自相关长度b类似,估计横向自相关长度a同样基于反演思想,区别在于其数据基础为地震数据而非测井数据。由于地震数据具有良好的横向连续性,使用常规反演方法也能获取稳定且连续的横向自相关长度a。此外,估计角度参数θ需要根据叠后地震剖面揭示的地层倾角确定。
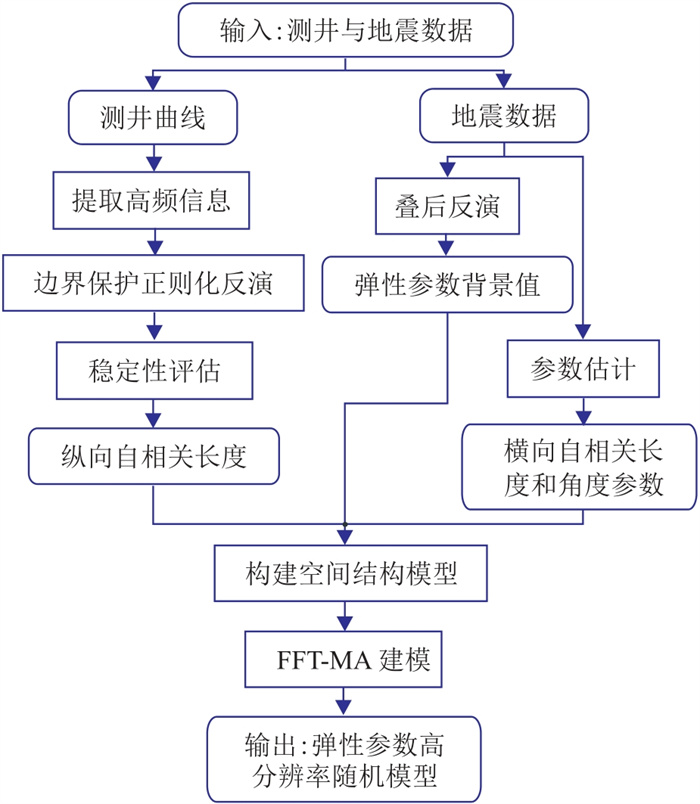
在分别估计了a、b以及θ后,根据式(2)得到优化的自相关函数即空间结构模型。然后,将其用于FFT-MA建模,构建符合实际空间结构的高分辨率弹性参数随机模型(图 2)。
|
图 2 本文随机建模方法的实现流程 |
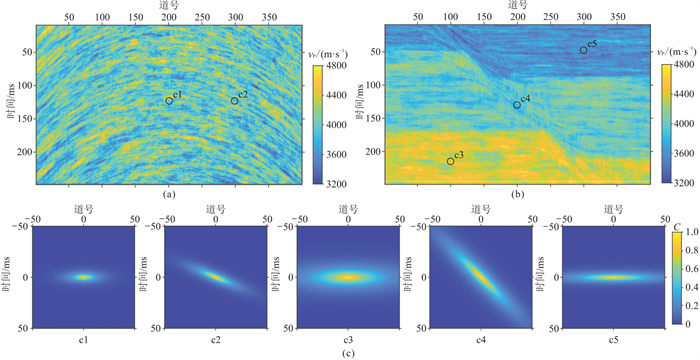
FFT-MA方法的优势在于能够构建具有非平稳空间结构的复杂模型。褶皱和断层是典型的复杂地质构造。图 3a和图 3b展示了基于非平稳空间结构模型的背斜和断层构造的FFT-MA建模结果。表 1为图 3a和图 3b五点的结构参数。该背斜构造的空间结构模型从轴部到两翼逐渐变化:横向自相关长度a由10道逐渐增大至20道;角度参数θ由0°逐渐增大至45°;纵向自相关长度b始终为3 ms。对比轴部c1点与翼部c2点空间结构模型,可以发现后者具有更大的横向相关性,而且横向相关性主方向是斜的。相应地,对比图 3a中建模点c1和c2,可以发现c2附近建模结果的横向连续性比c1强,同时层位倾斜。图 3b中断层构造空间结构模型的非平稳性体现在纵向自相关长度在由浅到深三个地层中分别为2、4和6 ms,同时在断层面角度参数θ为45°。对比c3点和c5点的结构模型,可以发现上部的c5点比下部的c3点具有更小的纵向相关性。相应地,随机模型对上部地层的刻画比下部更薄。此外,c4点的倾斜空间结构模型,用以约束建模能够描述断层构造。以上基于理论模型的测试表明,FFT-MA建模结果能够基于非平稳空间结构模型有效描述褶皱和断层等复杂地质构造。
|
图 3 理论模型FFT-MA随机建模结果及其空间结构模型 (a) 背斜模型(背景值为3600 m/s,标准差为100 m/s,两翼倾角为0~45°);(b)断层模型(地层背景值分别为3600、4000和4000 m/s,标准差为100 m/s,断面倾角为45°);(c)图a、图b不同位置建模点的空间结构模型 |
|
|
表 1 背斜和断层模型不同位置的结构参数 |
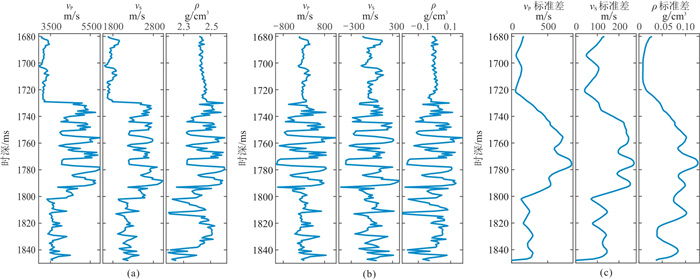
研究区内A井的三弹性参数(纵波速度vP、横波速度vS和密度ρ)测井曲线如图 4a所示,图 4b为去除低频趋势的高频成分,图 4c为描述测井曲线扰动大小的标准差。使用测井曲线高频成分估计纵向自相关长度b(t)。已知采样间隔为1 ms的测井曲线长度为168 ms。设置50 ms的分段长度和1 ms的滑动距离,将测井曲线划分为119个片段。使用模拟退火算法,以式(11)作为目标函数,分别得到常规弹性三参数的b(t)三次反演结果(图 5);以式(12)作为目标函数,将权重参数λ设置为0.03,尺度参数δ设置为0.01,分别得到边界保护正则化约束下的弹性三参数的b(t)三次反演结果(图 6)。
|
图 4 弹性三参数测井曲线(a)及其高频成分(b)和标准差(c) |
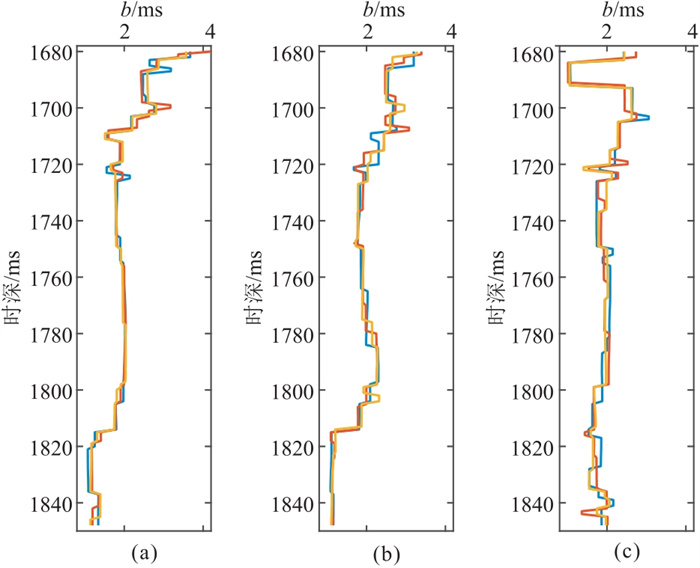
|
图 6 基于边界保护正则化的b(t)反演结果 (a)vP;(b)vS;(c)ρ |
对比图 5和图 6可以发现,常规和边界保护正则化约束下的b(t)反演结果随深度具有相同的变化趋势。对于纵波速度和横波速度,b(t)随着深度的增加而减小,且大致以1710和1810 ms为分界线划分为三个层段,分别标志着大、中和小纵向相关性;对于密度,b(t)在浅层变化剧烈,在1730 ms以下的变化相对平稳,标志着相对稳定的纵向相关性。图 4b显示的测井曲线纵向相关性变化规律与以上结论基本一致。尽管密度对应的b(t)在浅部的剧烈变化似乎与测井曲线并不一致,这可能是浅部太小的密度曲线扰动导致的计算误差。
然而,b(t)的多次反演结果揭示了常规反演方法的不稳定性。尽管总体上保持一致,局部b(t)反演结果存在明显的差异。以多次b(t)反演结果之间的平均相关系数衡量反演的稳定性,常规反演方法对应的三弹性参数b(t)平均相关系数分别为0.882、0.866和0.735。与之相比,边界保护正则化下的b(t)反演结果则表现出了更强的稳定性,其三弹性参数的b(t)平均相关系数分别为0.970、0.965和0.886。稳定的b(t)反演结果有助于构建更精确的FFT-MA随机模型。此外,边界保护正则化还具有另一优势,即能够保留参数的边界特征,从而辅助识别储层边界。纵向自相关长度b(t)的突变边界呈现出边界两侧显著的纵向相关性差异。以图 6中所示的1685、1708和1815 ms为例,b(t)反演结果展现出明显的边界特征,或许可以作为划分储层的依据。
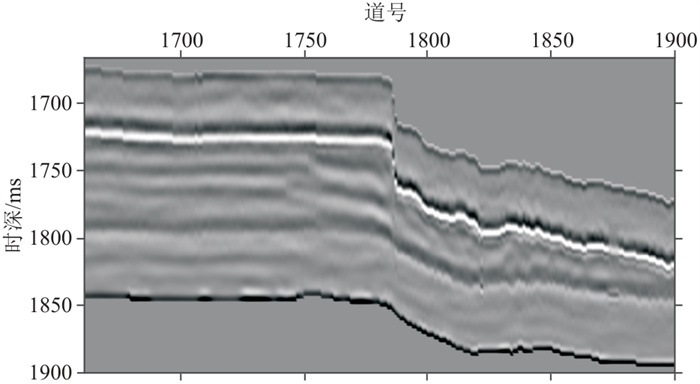
截取过A井叠后地震剖面如图 7所示,A井位于第1729道。储层在第1661~第1775道范围内大致为水平地层,在第1775道附近存在明显的断层构造,在第1775~第1850道范围内为向斜构造,而在第1850~第1900道范围内近似为单斜地层。使用真实地震记录估计横向自相关长度a(x, t),结果如图 8所示。可见a(x, t)在剖面上呈现非平稳的变化特征,揭示了储层横向相关性的非平稳变化。同时,a(x, t)的低值主要集中在断层带和褶皱附近,这说明断层和褶皱可能导致横向连续性降低。此外,横向自相关长度a(x, t)总体介于9.0~10.5倍道间距之间,并没有非常显著的差异。
|
图 7 过A井叠加剖面 |
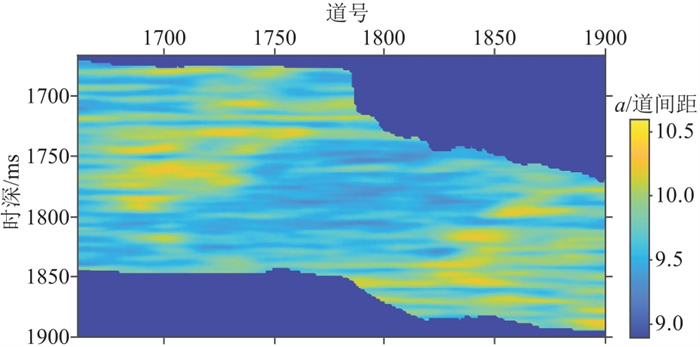
|
图 8 横向自相关长度 |
为验证本文方法构建的空间结构模型的准确性,同时凸显在构建非平稳空间结构模型方面的优势,对比利用变差分析方法构建的储层空间结构模型。经过实验,选取球状理论模型拟合变差函数。球状模型可表示为
| $ \gamma \left(h\right)=\left\{\begin{array}{l}0\begin{array}{cc}& h=0\end{array}\\ {c}_{0}+c\left(\frac{3h}{2\alpha }-\frac{{h}^{3}}{2{\alpha }^{3}}\right)\\ {c}_{0}+c\begin{array}{cc}& h > \alpha \end{array}\end{array}\right.\begin{array}{cc}& 1 < h\le \alpha \end{array} $ | (14) |
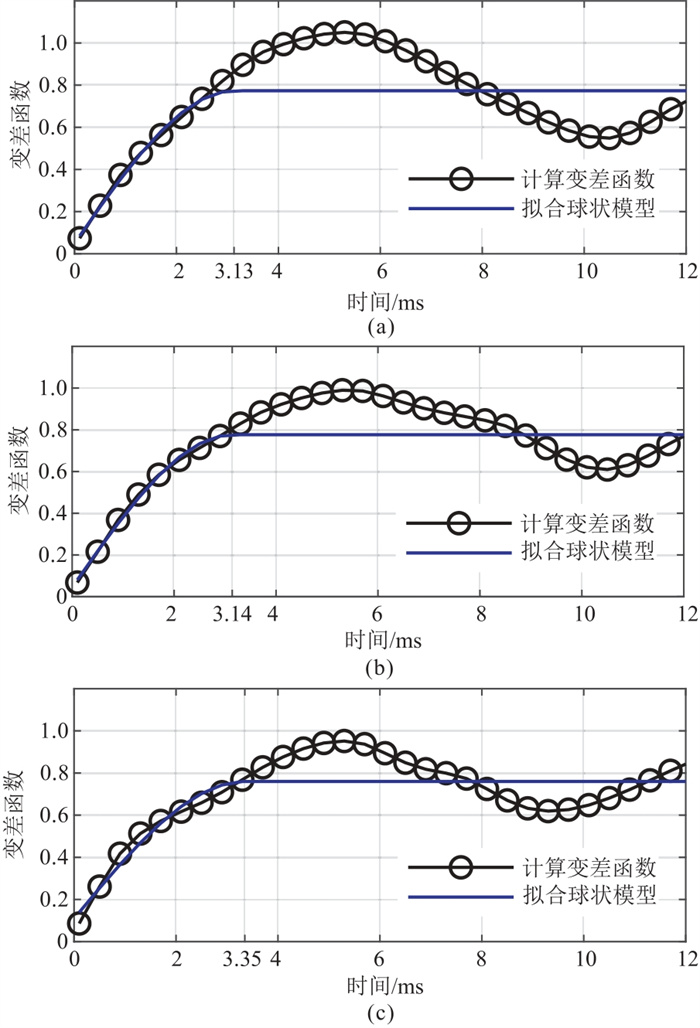
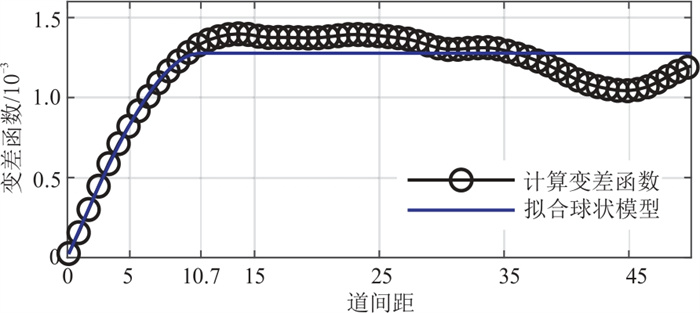
式中:γ为变差函数值;h为滞后距;c0为块金值;c为基台值;α为变程。图 9为使用三弹性参数测井曲线构建的纵向变差函数,其纵向变程参数分别为3.13、3.14和3.35 ms。图 10为使用地震记录构建的横向变差函数,其横向变程参数为10.7倍道间距。对比本文方法获取的纵向和横向自相关长度可知,虽然计算方法不同导致了两种方法获取的结构参数值有所差异,但是不同弹性参数、不同方向对应的结构参数的相对大小是一致的。然而,序贯高斯模拟方法要求使用平稳的空间结构模型,无论是横向相关性、纵向相关性或角度都是全局相同的。因此其构建的空间结构模型无法描述空间相关性的非平稳特征。
|
图 9 计算与拟合的纵向变差函数对比 (a)vP;(b)vS;(c)ρ |
|
图 10 计算与拟合的横向变差函数对比 |
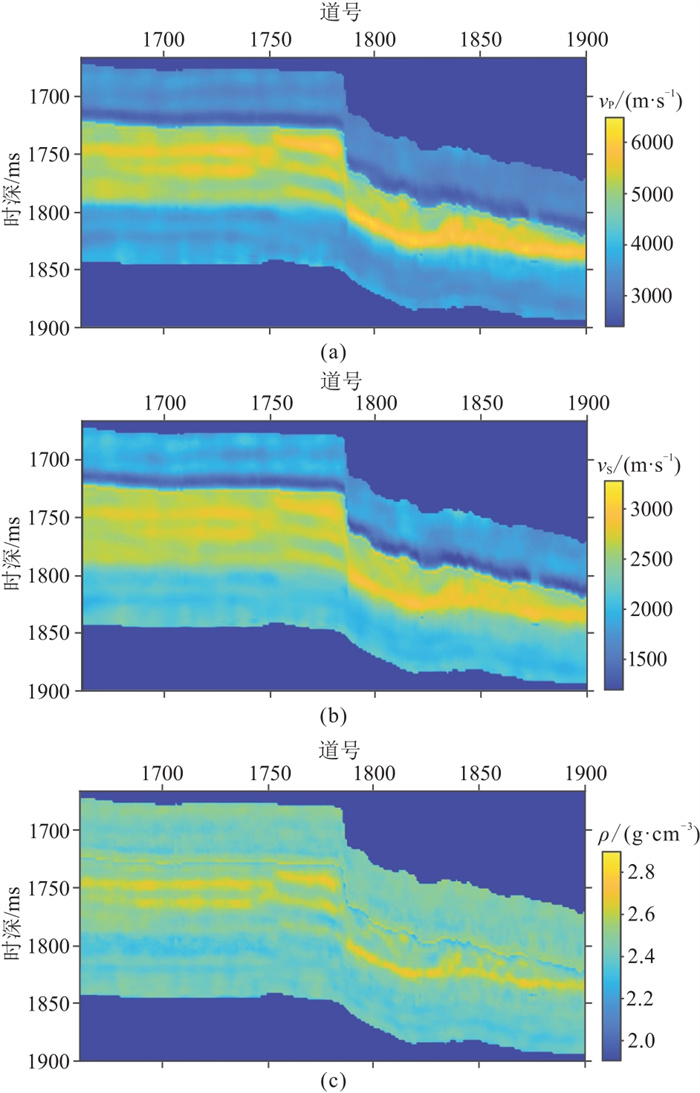
首先,用井旁道进行一维垂向非平稳FFT-MA随机建模实验。图 11为叠后地震反演获取的三弹性参数剖面m0(x, t)。已知本文研究的A井位于剖面第1729道,将三弹性参数在该道的反演结果m0(t)作为井旁道随机模型的背景值。利用基于测井数据和地震数据分别估计的测井纵向自相关长度b(t)和井旁道横向自相关长度a(t)和角度参数θ(t),构建优化的空间结构模型C(t)并进行FFT-MA随机建模。建模使用的扰动标准差如图 4c所示。
|
图 11 三弹性参数反演剖面 (a)vP;(b)vS;(c)ρ |
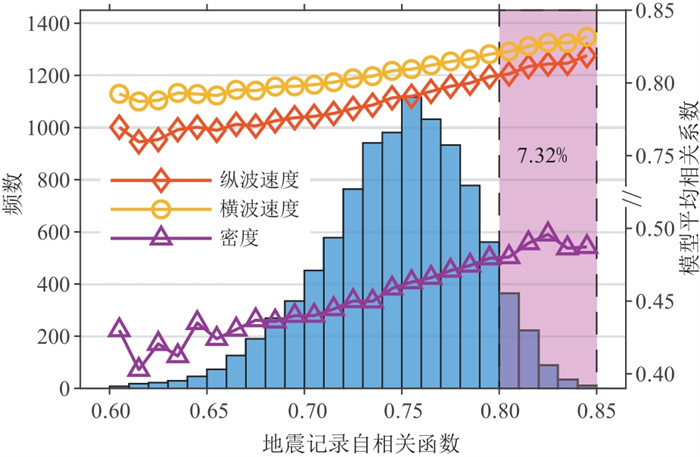
由于FFT-MA随机模型的随机性较强、稳定性较低,因此引入地震约束以提高随机模型的稳定性。在井旁道进行10000次独立的弹性三参数FFT-MA随机建模,利用Fatti近似式计算合成地震记录并计算与真实地震记录的相关系数,统计结果如图 12柱状图所示。可见地震记录相关系数近似正态分布,均值约为0.75且分布范围较大,这体现了FFT-MA随机模型的不稳定性。将随机模型按照地震记录相关系数等间隔分组并统计各组三弹性参数模型的平均相关系数如图 12折线所示。其中,地震记录相关系数高于0.8的随机模型约占所有建模结果的7.32%。可见地震记录相关系数越高模型平均相关系数也越高,使用地震数据作为约束能够显著提高随机模型的稳定性。
|
图 12 10000次FFT-MA随机建模结果地震记录相关系数与模型平均相关系数统计图 |
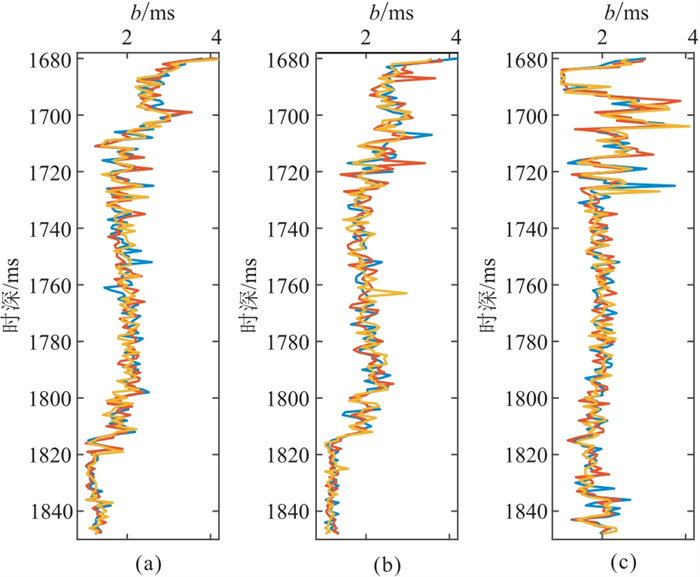
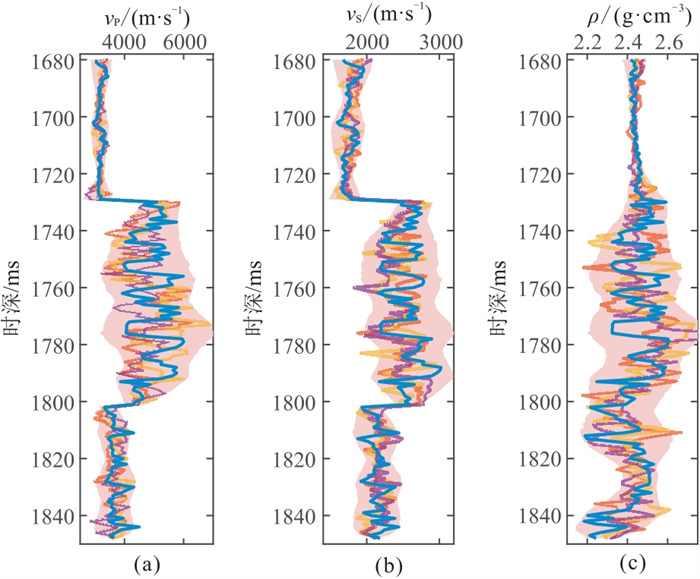
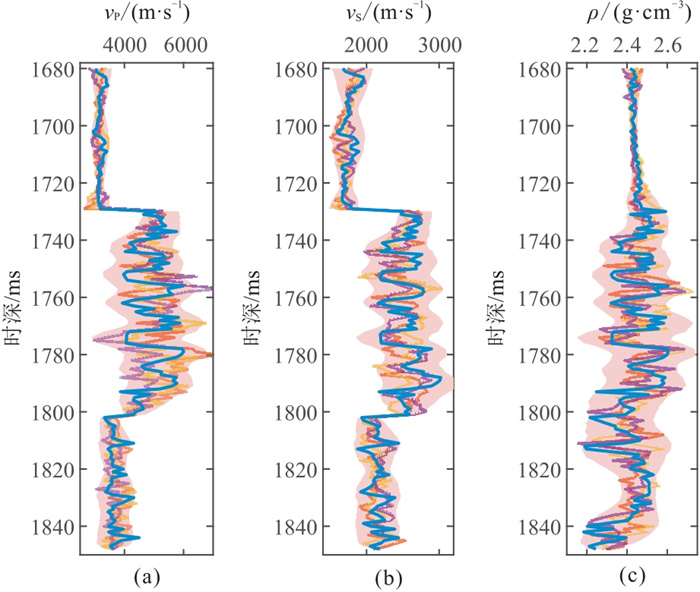
图 13为无地震约束的井旁道FFT-MA随机建模结果,图 14为地震约束下合成地震记录与实际地震记录相关系数高于0.8的井旁道FFT-MA随机建模结果。可见地震约束下的随机模型95%置信区间小于无地震约束的随机模型,且与测井曲线的拟合程度更高,证明了地震约束能够有效提高随机模型的稳定性和准确性。
|
图 13 无地震约束井旁道随机建模结果 (a)vP;(b)vS;(c)ρ。粗线为测井数据,细线为三次建模结果,阴影部分为95%置信区间。 |
|
图 14 地震约束下井旁道随机建模结果 (a)vP;(b)vS;(c)ρ。粗线为测井数据,细线为三次建模结果,阴影部分为95%置信区间。 |
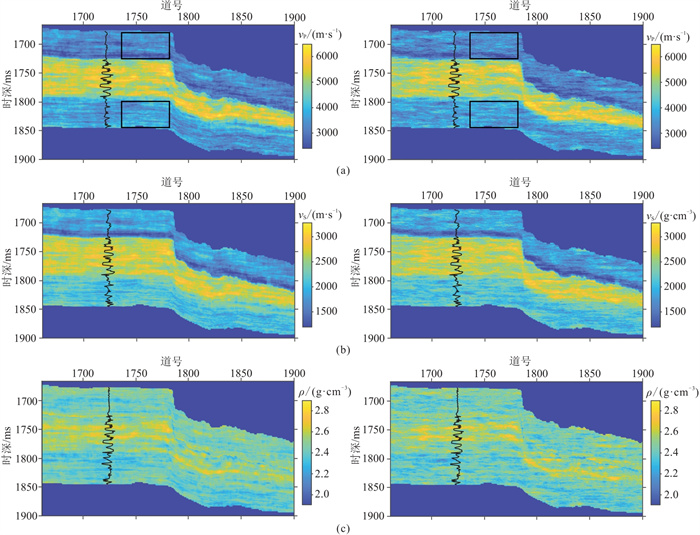
然后,在整个剖面进行二维非平稳FFT-MA随机建模实验。将测井曲线标准差σm(t)和纵向自相关长度b(t)顺层延拓得到剖面标准差σm(x, t)和纵向自相关长度b(x, t)。利用图 7所示的叠加地震剖面估计储层角度参数θ(x, t)。随后根据式(2)计算储层非平稳空间结构模型C(x, t)。以图 11所示的三弹性参数地震反演剖面m0(x, t)为背景值,得到FFT-MA随机模型如图 15左所示。相比于图 11所示的地震反演模型,FFT-MA随机模型的分辨率显著提高,实现了对细节的精细表征。同时,利用前述基于变差分析获取的空间结构模型,使用序贯高斯协模拟方法,以测井曲线作为条件数据得到三弹性参数随机模型如图 15右所示。可见,基于序贯高斯协模拟的随机模型同样具有很高的分辨率,其对细节的精细表征能力与FFT-MA随机模型相当。然而,与序贯高斯协模拟方法相比,本文提出的FFT-MA随机建模方法的优势在于能够使用非平稳的空间结构模型描述空间相关性的非平稳特征。由图 6可知纵波速度的纵向自相关长度b(t)由浅到深逐渐降低,对应了空间结构模型的变化。对比图 15a中两矩形框内的随机建模结果,可以发现:序贯模型在1810~1840 ms范围内和在1680~1710 ms范围内刻画的薄层厚度几乎没有变化;而FFT-MA模型在1810~1840 ms范围内比在1680~1710 ms范围内刻画了更薄的地层结构。此外,序贯高斯模拟方法要求空间结构模型的角度恒定,而FFT-MA方法允许空间结构模型设置非平稳的角度参数。观察图 15右的序贯高斯模拟模型,其高频成分只能刻画平行地层,无法体现角度变化。然而对于图 15左的FFT-MA模型,在1661~1775道范围内刻画了水平地层,在1775道附近刻画了断层构造,在1775~1850道范围内刻画了向斜构造,在1850~1900道范围内刻画了单斜地层。这说明使用非平稳空间结构模型的FFT-MA随机建模方法能够有效刻画多种复杂的地质构造从而实现复杂地层建模。
|
图 15 本文的FFT-MA随机建模结果(左)与序贯高斯协模拟随机建模结果(右)的对比 (a)vP;(b)vS;(c)ρ |
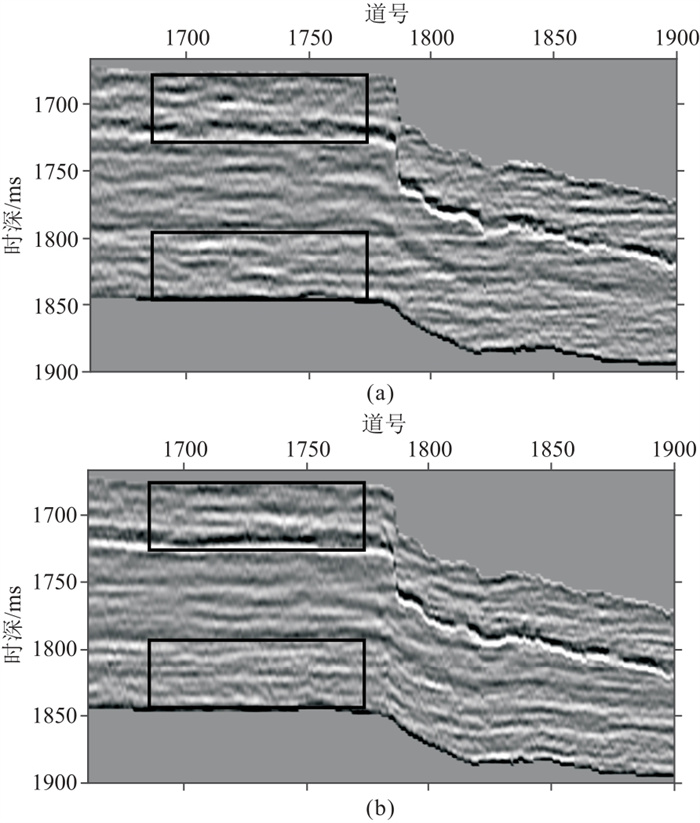
为了提高随机模型的稳定性和准确性,对基于序贯高斯协模拟方法和FFT-MA方法的随机模型施加了地震约束,合成地震记录如图 16所示。二者的合成地震记录都与真实地震记录具有较高的一致性,相关系数皆高于0.85。同时,两种随机模型对应的合成地震记录都包含更丰富的细节信息,分辨率显著提高。合成地震记录再次证明了FFT-MA方法构建复杂模型的有效性。对比图 16a矩形框内的地震记录说明序贯模型无法根据实际调整纵向相关性的变化;而对比图 16b矩形框内的地震记录验证了FFT-MA模型根据测井信息在深度增大时减小了模型的纵向相关性。此外,相对图 7的真实地震记录,序贯模型的合成地震记录在所有位置叠加的都是同相轴水平的波形,完全无法重现地层的真实形态。而FFT-MA模型的合成地震记录有效重现了的水平地层、断层、向斜和单斜地层等真实构造,实现了复杂储层的高分辨率建模。
|
图 16 两种方法建模结果的合成地震剖面对比 (a)序贯高斯协模拟;(b)FFT-MA随机建模 |
(1) 通过最小化随机模型与测井数据和地震数据的空间结构差异分别反演纵向自相关长度和横向自相关长度,准确构建了非平稳空间结构模型。
(2) 将边界保护正则化引入纵向自相关长度的反演显著提高了反演结果的稳定性,同时保留了纵向自相关长度反演结果的边界特征。
(3) 通过对FFT-MA随机模型施加地震约束,显著提高了随机模型的稳定性和准确性。
(4) 与基于序贯高斯协模拟的随机建模方法相比,使用非平稳空间结构模型的FFT-MA随机建模方法能够有效刻画多种复杂的地质构造从而实现复杂储层建模。
本文FFT-MA随机建模方法局限性与可能的改进:
(1) 基于边界保护正则化反演的纵向自相关长度为储层边界识别提供了可能的依据,但效果和准确性仍需实际测井解释标定的进一步分析验证;
(2) 本文使用真实地震记录与合成地震记录之间的相关系数筛选随机模型,其稳定性和准确性的提升效果远低于地震随机反演方法。因此,将本文方法与地震随机反演方法结合进一步提升随机模型的稳定性和准确性是今后的研究方向。
| [1] |
叶端南, 印兴耀, 王璞, 等. 砂泥岩储层岩石物理交会模板构建[J]. 地球物理学进展, 2015, 30(2): 758-768. YE Duannan, YIN Xingyao, WANG Pu, et al. The build of rock physics cross plot template for sand shale reservoir[J]. Progress in Geophysics, 2015, 30(2): 758-768. |
| [2] |
杨午阳, 王丛镔. 利用叠前AVA同步反演预测储层物性参数[J]. 石油地球物理勘探, 2010, 45(3): 414-417. YANG Wuyang, WANG Congbin. Utilizing pre-stack simultaneous inversion to predict reservoir physical properties[J]. Oil Geophysical Prospecting, 2010, 45(3): 414-417. |
| [3] |
XU D H, HAN T C, LIU S B, et al. Effects of randomly orienting penny‑shaped cracks on the elastic properties of transversely isotropic rocks[J]. Geophysics, 2020, 85(6): MR325-MR340. |
| [4] |
HAO F. Enrichment mechanism and prospects of deep oil and gas[J]. Acta Geologica Sinica, 2022, 96(3): 742-756. |
| [5] |
刘震, 张军华, 于正军, 等. 非常规储层脆性研究进展及展望[J]. 石油地球物理勘探, 2023, 58(6): 1499-1507. LIU Zhen, ZHANG Junhua, YU Zhengjun, et al. Progress and prospects of brittleness research in unconventional reservoirs[J]. Oil Geophysical Prospecting, 2023, 58(6): 1499-1507. |
| [6] |
肖灯意, 谢瑾, 李建林, 等. 碳酸盐岩非常规天然气综合评价技术——以阿联酋西部Diyab组为例[J]. 石油地球物理勘探, 2023, 58(增刊1): 97-104. XIAO Dengyi, XIE Jin, LI Jianlin, et al. Comprehensive evaluation technology of unconventional carbonate gas: Case study on Diyab formation in western UAE[J]. Oil Geophysical Prospecting, 2023, 58(S1): 97-104. |
| [7] |
印兴耀, 贺东阳, 宗兆云, 等. 结合序贯指示模拟的贝叶斯高斯混合线性反演[J]. 地球物理学报, 2019, 62(12): 4805-4816. YIN Xingyao, HE Dongyang, ZONG Zhaoyun, et al. Bayesian Gaussian mixture linear inversion combined with sequential indicator simulation[J]. Chinese Journal of Geophysics, 2019, 62(12): 4805-4816. |
| [8] |
PEBESMA E J, WESSELING C G. Gstat: a program for geostatistical modelling, prediction and simulation[J]. Computers & Geosciences, 1998, 24(1): 17-31. |
| [9] |
MIROWSKI P W, TETZLAFF D M, DAVIES R C, et al. Stationarity scores on training images for multipoint geostatistics[J]. Mathematical Geosciences, 2009, 41: 447-474. |
| [10] |
乐友喜, 曾勉, 问雪, 等. 利用序贯高斯随机模拟分析构造图的不确定性[J]. 石油地球物理勘探, 2017, 52(2): 333-339. YUE Youxi, ZENG Mian, WEN Xue, et al. Structure uncertainty analysis based on sequential Gaussian stochastic simulation[J]. Oil Geophysical Prospecting, 2017, 52(2): 333-339. |
| [11] |
李祺鑫, 罗亚能, 张生, 等. 高分辨率波阻抗贝叶斯序贯随机反演[J]. 石油地球物理勘探, 2020, 55(2): 389-397. LI Qixin, LUO Yaneng, ZHANG Sheng, et al. High resolution wave impedance Bayesian sequential random inversion[J]. Oil Geophysical Prospecting, 2020, 55(2): 389-397. |
| [12] |
SOARES A. Direct sequential simulation and cosimulation[J]. Mathematical Geology, 2001, 33(1): 911-926. |
| [13] |
刘兴业, 李景叶, 陈小宏, 等. 联合多点地质统计学与序贯高斯模拟的随机反演方法[J]. 地球物理学报, 2018, 61(7): 2998-3007. LIU Xingye, LI Jingye, CHEN Xiaohong, et al. A stochastic inversion method integrating multi-point geostatistics and sequential Gaussian simulation[J]. Chinese Journal of Geophysics, 2018, 61(7): 2998-3007. |
| [14] |
CORDUA K S, HANSEN T M, GULBRANDSEN M L, et al. Mixed‑point geostatistical simulation: A combination of two-and multiple-point geostatistics[J]. Geophysical Research Letters, 2016, 43(17): 9030-9037. |
| [15] |
RAVALEC M L, NOETINGER B, HU L Y. The FFT moving average (FFT-MA) generator: An efficient numerical method for generating and conditioning Gaussian simulations[J]. Mathematical Geology, 2000, 32(6): 701-723. |
| [16] |
杨修伟, 朱培民, 毛宁波, 等. 基于FFT-MA的随机介质建模方法[J]. 地球物理学报, 2018, 61(12): 5007-5018. YANG Xiuwei, ZHU Peimin, MAO Ningbo, et al. Random medium modeling based on FFT‑MA[J]. Chinese Journal of Geophysics, 2018, 61(12): 5007-5018. |
| [17] |
YANG X W, MAO N B, ZHU P M. Hybrid inversion of reservoir parameters based on cosimulation and the gradual deformation method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60(1): 1-11. |
| [18] |
王保丽, 孙瑞莹, 印兴耀, 等. 基于Metropolis抽样的非线性反演方法[J]. 石油地球物理勘探, 2015, 50(1): 111-117. WANG Baoli, SUN Ruiying, YIN Xingyao, et al. Nonlinear inversion method based on Metropolis sampling[J]. Oil Geophysical Prospecting, 2015, 50(1): 111-117. |
| [19] |
孙瑞莹, 印兴耀, 王保丽, 等. 基于Metropolis抽样的弹性阻抗随机反演[J]. 物探与化探, 2015, 39(1): 203-210. SUN Ruiying, YIN Xingyao, WANG Baoli, et al. Stochastic inversion of elastic impedance based on Metropolis sampling algorithm[J]. Geophysical and Geochemical Exploration, 2015, 39(1): 203-210. |
| [20] |
YIN X Y, SUN R Y, WANG B L, et al. Simultaneous inversion of petrophysical parameters based on geostatistical a priori information[J]. Applied Geophysics, 2014, 11(1): 311-320. |
| [21] |
顾元, 朱培民, 李辉, 等. 二维叠后地震数据的平稳随机介质参数估计[J]. 地球物理学报, 2014, 57(7): 2291-2301. GU Yuan, ZHU Peimin, LI Hui, et al. Estimation of 2D stationary random medium parameters from post-stack seismic data[J]. Chinese Journal of Geophysics, 2014, 57(7): 2291-2301. |
| [22] |
IRVING J, KNIGHT R, HOLLIGER K. Estimation of the lateral correlation structure of subsurface water content from surface-based ground-penetrating radar reflection images[J]. Water Resources Research, 2009, 45(12): 1-14. |
| [23] |
IRVING J, HOLLIGER K. Geostatistical inversion of seismic and ground-penetrating radar reflection images: What can we actually resolve?[J]. Geophysical Research Letters, 2010, 37(21): 1-5. |
| [24] |
SCHOLER M, IRVING J, HOLLIGER K. Estimation of the correlation structure of crustal velocity heterogeneity from seismic reflection data[J]. Geophysical Journal International, 2010, 183(3): 1408-1428. |
| [25] |
ZHANG H B, SHANG Z P, YANG C C. A non-linear regularized constrained impedance inversion[J]. Geophysical Prospecting, 2007, 55(6): 819-833. |
| [26] |
CHERNOV L A, SILVERMAN R A, MORSE P M. Wave propagation in a random medium[J]. Journal of Applied Mechanics, 1961, 28(2): 318-319. |
| [27] |
奚先, 姚姚. 随机介质模型的模拟与混合型随机介质[J]. 地球科学, 2002, 27(1): 67-71. XI Xian, YAO Yao. Simulation of random media models and mixed random media[J]. Earth Science, 2002, 27(1): 67-71. |



 曾繁鑫, 江苏省南京市江宁区佛城西路8号河海大学地球科学与工程学院,211100。Email:
曾繁鑫, 江苏省南京市江宁区佛城西路8号河海大学地球科学与工程学院,211100。Email: