2. 同济大学海洋与地球科学学院, 上海 200092;
3. 南京大学地球科学与工程学院, 江苏南京 210023;
4. 中国石化西北油田分公司勘探开发研究院, 新疆乌鲁木齐 830011
2. School of Ocean and Earth Science, Tongji University, Shanghai 200092, Chin;
3. School of Earth Sciences and Engineering, Nanjing University, Nanjing, Jiangsu 210023, China;
4. Exploration and Development Research Institute, SINOPEC Northwest Oilfield Company, Urumqi, Xinjiang 830011, China
塔里木盆地碳酸盐岩缝洞体具有埋藏较深和纵向、横向非均质性强的特点,这给缝洞体的精细预测带来了较大困难,成为了制约后续油气高效开发的关键问题[1-2]。为满足精度需求,目前储层研究需要从前期的定性分析转变为定量预测,从而能更好地开展井位部署、储量计算等。
塔里木盆地缝洞型储层主要受控于岩溶作用,岩溶缝洞体被流体充填,具有低阻抗特征。岩溶缝洞体在地震剖面上表现为“串珠”状反射特征。众多学者据此开展研究工作。
在地震资料采集方面,王彦峰等[3]、张军华等[4]分别从分辨率和信噪比两个角度进行了采集参数优化及观测系统设计,提高了岩溶缝洞体的资料品质。在物理模拟和数值模拟、溶洞“串珠”状反射形成机理和储层特征分析方面,魏建新等[5]建立了不同尺度孔洞模型,并采用地震物理模拟技术对孔洞绕射特征进行了详细分析,研究表明溶洞绕射能量与其尺度、形态均有明显关系。朱生旺等[6]采用随机模型方法,分析了不同孔洞的尺度、分布密度与模型参数之间的关系,提高了孔洞型油气储层的描述精度。赵群等[7]建立了不同形态、不同尺度及不同充填物溶洞物理模型,分析了“串珠”状地震反射特征的规律,建立了地质体特征与地震反射特征之间的关系。李凡异等[8]开展了三维物理模型的制作,讨论了孔洞储层的纵、横向分辨率及体积校正问题,为实际孔洞储集体体积估算提供了思路。
在地震资料成像方面,Wu等[9]开展了散射波成像,胡鹏飞[10]提出了缝洞型储层高精度成像技术,均提高了岩溶缝洞体的成像精度。
在缝洞体储层预测方面,形成了岩相分类[11]、频谱分解[12]、叠前方位各向异性裂缝检测[13]、内部结构识别[14]和异常反射智能检测[15]等方法。
针对缝洞体尺度,Zhu等[16]提出了基于叠前分频振幅差异的缝洞体尺度预测方法,初步实现了缝洞体尺度的预测。此外,朱博华等[17]、杨江峰等[18]提出了基于叠前分频资料的小尺度缝洞体检测方法,提高了缝洞体识别的精度。在缝洞体校正时,常采用振幅属性,但振幅属性刻画的尺度远远大于实际地质体尺度,这需要对振幅阈值进行校正才能得到更为准确的预测结果。同时,从理论上讲,由于子波旁瓣效应的影响,振幅属性直接刻画缝洞体会存在较大误差。
在缝洞体储层定量预测方面,地震反演[19]、AVO技术[20]等均有效提高了预测结果的定量化程度。地震反演能较好地弱化子波旁瓣效应,预测缝洞体发育特征,实现缝洞体的准确刻画。但是,同样存在缝洞体属性(阻抗)值域选取的不确定性问题。有学者采用多属性融合、井震标定等方法确定属性值域,取得了一定的效果,但由于缝洞体的强非均质性特点,这些方法仍然难以满足实际需求。
综上所述,本文结合叠前分频尺度预测和阻抗反演两者的优势,提出基于分频尺度约束的缝洞体尺度校正和空间定位方法。首先利用叠前分频方法对缝洞体尺度进行预测,然后用此尺度参数对缝洞体阻抗阈值进行标定,最终实现缝洞体的尺度校正和空间的准确定位。模型测试和实际资料应用均验证了方法的可靠性和适用性。
1 方法原理 1.1 地震波调谐理论Widess[21]详细讨论了单套岩层厚度对波形反射特征的影响,当岩层厚度为1/4波长时,岩层顶、底波形干涉,波峰、波谷相对振幅达到最大,此时的岩层厚度称为调谐厚度。缝洞体可以看作是纵向有一定厚度的地质体,在地震剖面上表现为明显的“串珠”状响应特征[5-9]。缝洞体的尺度预测与地震资料的频带特征、纵向分辨能力息息相关[22],缝洞体的地震反射的振幅变化同样遵循地震波调谐原理。
针对缝洞体尺度,可以通过分频方法将地震信号分解到不同的频段,绘制缝洞体位置波峰、波谷相对振幅—频率曲线,将曲线峰值频率作为缝洞体的调谐频率。在地层速度已知的情况下,可求取调谐厚度,即缝洞体的纵向尺度
| $ R=\frac{\lambda }{4}=\frac{v}{4f} $ | (1) |
式中:
由式(1)可见,当调谐频率较低时,对应的调谐厚度较大,缝洞体尺度较大;当调谐频率较高时,对应的调谐厚度较小,缝洞体尺度较小。因此,可以利用地震资料的不同频带信息,开展缝洞体多尺度识别和预测,实现缝洞体的尺度预测和空间校正,从而大幅度提高缝洞体预测精度。
1.2 叠前CMP资料分频偏移利用分频地震资料可以挖掘更多的地质信息,可用于断层刻画、储层预测以及含油气检测等。常用分频方式包括叠后分频、叠前CRP道集分频和叠前CMP道集分频等。其中叠前CMP道集分频是对全频带CMP道集先进行不同频带分频处理,再分别对不同频段的CMP道集进行偏移成像以获取不同频带的偏移剖面。
采用地震信号数字滤波方法可以实现分频处理,此过程会出现较明显的吉布斯现象[23],但可通过频域镶边、时域加窗弱化吉布斯效应。在实际资料中,叠后分频的吉布斯现象仍较为明显,波形特征容易发生畸变,分频效果(尤其在高频段)欠佳,不能满足生产需求。此外,道集的叠加过程为线性时不变过程,所以CRP道集分频与叠后分频在本质上是一致的,最终的成像效果也相同。
CMP道集分频技术可较好地弱化吉布斯效应[17],改善分频成像效果。因此,本文优选CMP道集分频方法。通过CMP道集分频可得到多个分频体,然后据此开展缝洞体调谐频率和调谐厚度的计算,从而可预测缝洞体的尺度。
1.3 调谐频率准确计算在实际资料处理中,分频数据的个数往往有限,一般为3~6个。在调谐频率计算过程中,只能基于少数几个散点进行判断而得到调谐频率的值。由于数据点有限,调谐频率的计算存在较大误差。参考高斯函数在光谱学领域的应用[24],本文采用高斯函数拟合方式求取准确的调谐频率。
高斯函数一维表达式为
| $ f\left(x\right)=a{\mathrm{e}}^{-\frac{{(x-b)}^{2}}{2{c}^{2}}} $ | (2) |
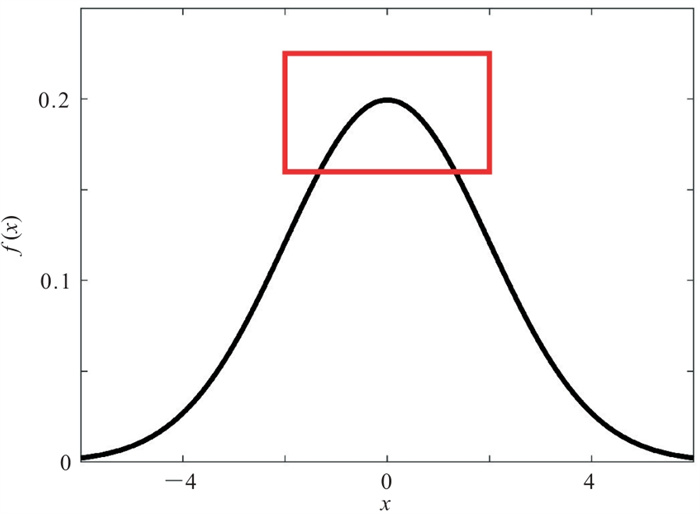
其一维图是特征对称钟状曲线。式中a、b、c为任意实数,其中a
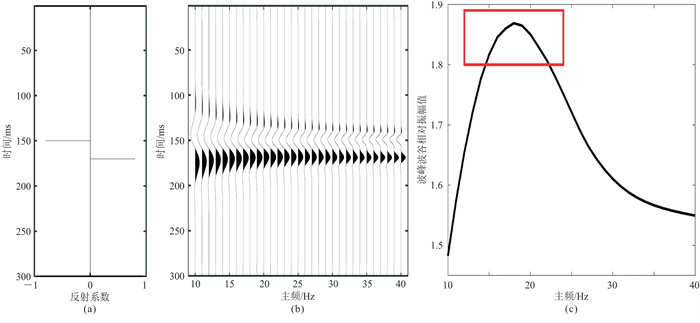
设定参数b=0,c=2,绘制高斯曲线如图 1所示。设计一套时间厚度为20 ms的地层(图 2a),采用零相位雷克子波进行褶积运算得到正演曲线(图 2b),雷克子波主频从10 Hz逐渐提高至40 Hz,并计算其理论调谐曲线(图 2c)。由图可知,在调谐点附近,散点的分布特征非常接近高斯函数表达式。由此考虑基于有限个散点(即多个分频数据体),利用高斯函数对调谐点附近多个散点进行拟合(图 1和图 2c红框所示),可得到光滑曲线。计算高斯曲线最大值(峰值频率)并将它作为调谐频率,由此可计算调谐厚度,从而提高缝洞体尺度预测的精度。
|
图 1 归一化高斯曲线 |
|
图 2 调谐曲线特征分析 (a)反射系数;(b)分频正演剖面;(c)调谐曲线 |
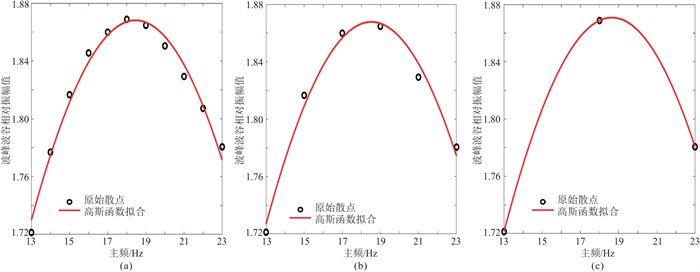
以图 2c为例,开展高斯函数散点拟合效果对比分析。对连续散点(间隔为1 Hz)进行高斯曲线拟合(图 3a),求取的调谐频率为18.46 Hz;抽稀散点,按间隔2 Hz进行高斯曲线拟合(图 3b),求取的调谐频率为18.53 Hz;按间隔5 Hz进行高斯曲线拟合(图 3c),求取的调谐频率为18.65 Hz。
|
图 3 高斯函数散点不同间隔拟合对比 (a)1 Hz;(b)2 Hz;(c)5 Hz |
由上述可知,在调谐点附近,基于有限个散点的高斯函数拟合方法能较准确地预测其调谐频率,误差很小,具有较好的稳定性和可靠性,可以在实际资料有限个分频数据中推广应用。
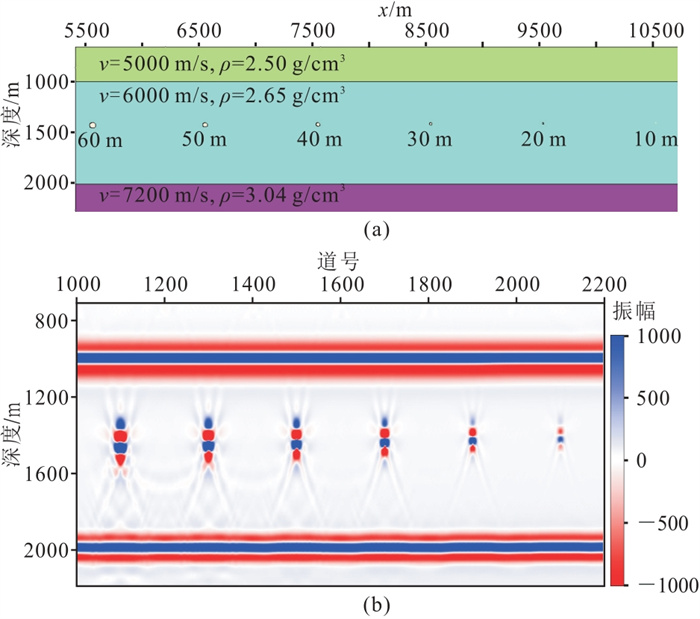
2 缝洞体尺度预测通过正演模拟验证分频尺度预测的有效性。设定模型(图 4a)观测系统长度为16 km,满覆盖长度为7 km,单点激发,双边接收,最大炮检距为3 km,炮间距为50 m,检波点间距为50 m,CDP间隔为25 m,正演网格为5 m×5 m。正演子波为30 Hz零相位雷克子波。
|
图 4 模型设计及成像剖面 (a)地质模型;(b)深度偏移剖面 |
分别设计6种不同尺度的圆形洞穴模型,直径分别为60、50、40、30、20和10 m。洞穴充填速度(v)为3600 m/s,密度(ρ)为2.29 g/cm3;围岩速度为6000 m/s,密度为2.65 g/cm3。洞穴具低阻抗特征。利用弹性波正演模拟算法进行正演,采用叠前深度偏移算法对其进行高精度成像。如图 4b所示,从左往右,缝洞体尺度从60 m逐渐减小至10 m。可以看出,洞穴绕射波能量收敛后,表现为“串珠”状地震反射特征,且洞穴尺度越大,“串珠”状反射特征越明显、反射能量越强。单个“串珠”表现为中间强波谷+强波峰组合、两侧为弱反射特征。随着洞穴尺度变小,“串珠”状反射特征明显减弱。
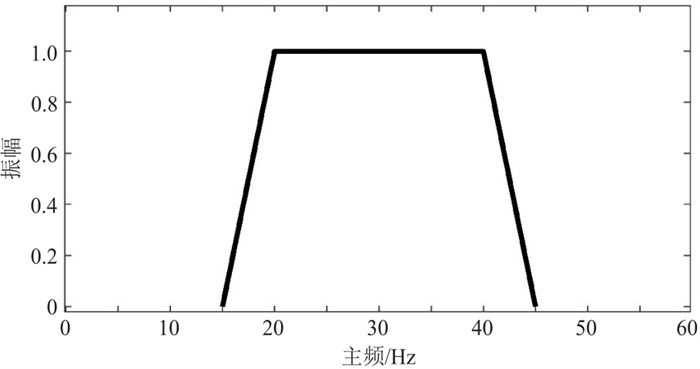
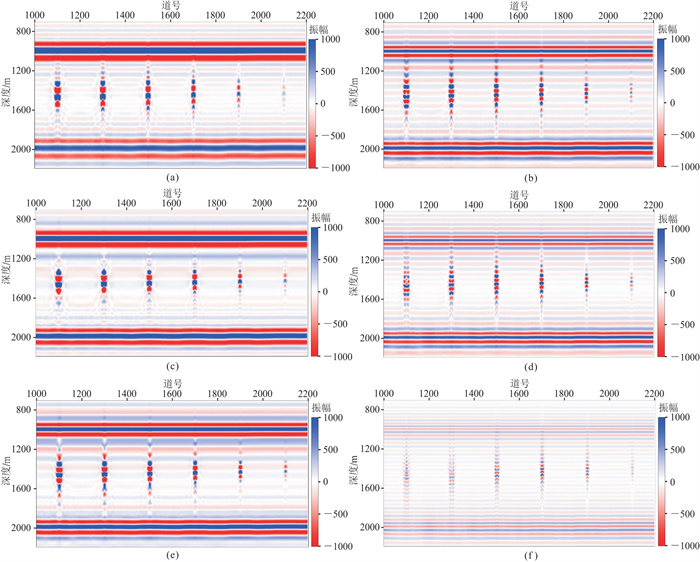
为了进一步研究不同尺度洞穴在不同地震频带下的响应特征,开展了针对模型的叠前分频处理。首先利用原始CMP道集进行分频处理,再对其进行叠前深度偏移。设置分频参数为6组,其主频和带宽分别为15 Hz和5~25 Hz、23 Hz和13~33 Hz、30 Hz和20~40 Hz、35 Hz和25~45 Hz、40 Hz和30~50 Hz、50 Hz和40~60 Hz,频域滤波器镶边统一为5 Hz,主频30 Hz分频处理滤波器如图 5所示。分频成像结果如图 6所示。为了突出CMP道集分频的优势,采用相同的分频参数对全频带叠前深度偏移剖面(图 4b)进行叠后分频处理,分频结果如图 7所示。
|
图 5 频域滤波器示意图 |

|
图 6 模型不同主频CMP道集分频成像剖面 (a)15 Hz;(b)23 Hz;(c)30 Hz;(d)35 Hz;(e)40 Hz;(f)50 Hz |
|
图 7 模型不同主频叠后分频剖面 (a)15 Hz;(b)23 Hz;(c)30 Hz;(d)35 Hz;(e)40 Hz;(f)50 Hz |
对比图 6与图 7可知,CMP道集分频的成像效果较好,“串珠”状特征保持较好,剖面特征自然;而叠后分频结果的吉布斯效应较为明显,中低频段结果相对稳定,但在高频段波形明显畸变,“串珠”拉长,缝洞体波形振幅、相位、频率特征被破坏。此外,高频分频剖面对于小尺度洞穴的刻画效果更好,响应特征明显增强;低频分频剖面对于大尺度洞穴的表征效果更好。
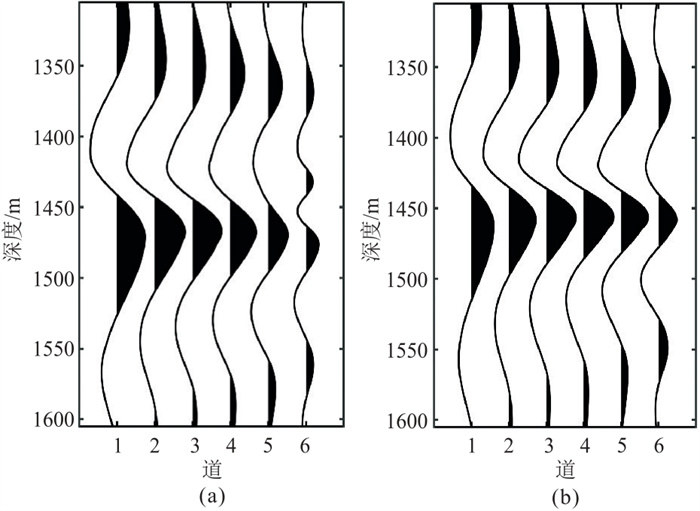
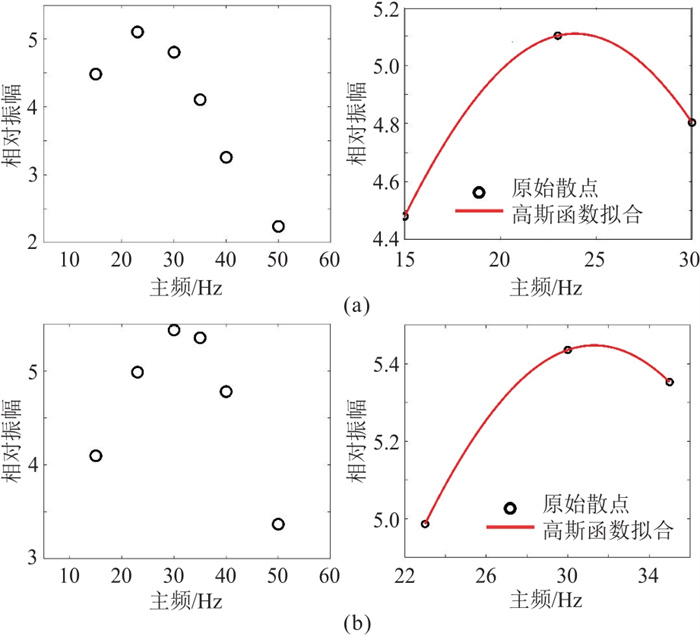
以60 m和50 m两个缝洞体为例,进行不同尺度预测效果分析。基于地震波调谐曲线计算准则,提取不同频带成像数据体“串珠”状反射中心处地震波形(图 8)。提取“串珠”状反射波峰到波谷的相对振幅,以散点的形式绘制成图,并对调谐点附近多个散点进行高斯函数拟合(图 9)。
|
图 8 不同尺度缝洞体过“串珠”位置波形 (a)60 m;(b)50 m 从左向右,各道主频依次为15、23、30、35、40和50 Hz。 |
|
图 9 不同尺度缝洞体调谐频率计算 (a)60 m;(b)50 m 左为缝洞体散点,右为缝洞体高斯拟合。 |
通过分频处理和调谐频率的准确计算,60 m缝洞体调谐频率为23.9 Hz,预测的调谐厚度(围岩速度为6000 m/s)为62.8 m;50 m缝洞体调谐频率为31.3 Hz,预测的调谐厚度为47.9 m,均与实际缝洞体尺度接近,误差较小。据此验证了基于调谐理论的缝洞体尺度预测结果的可靠性,这为后续实际资料中多尺度缝洞体预测提供了可靠依据。
3 实际资料应用 3.1 钻井情况分析研究区位于塔里木盆地Y工区,油气勘探目标为奥陶系碳酸盐岩缝洞体。根据前期成果部署了W1井。在钻探过程中,目的层有数段良好的荧光及槽面气泡等油气显示,初步判断该井附近有油气充注。但靶点位置未出现明显的放空、漏失等现象,未钻遇有效储集体,过井剖面和平面属性如图 10所示。由于该井为大斜度井,水平位移为1.4 km,从钻井工艺角度看,已经很难实现井轨迹调整、侧钻等操作,后续只能通过工程酸化压裂沟通附近缝洞体达到建产目标。从过井剖面(图 10a)可知,现有轨迹穿过缝洞体波谷位置,但由于波形放大效应,储集体规模比波形响应小很多。分析认为有利储集体发育在井轨迹下方,但具体尺度未知。
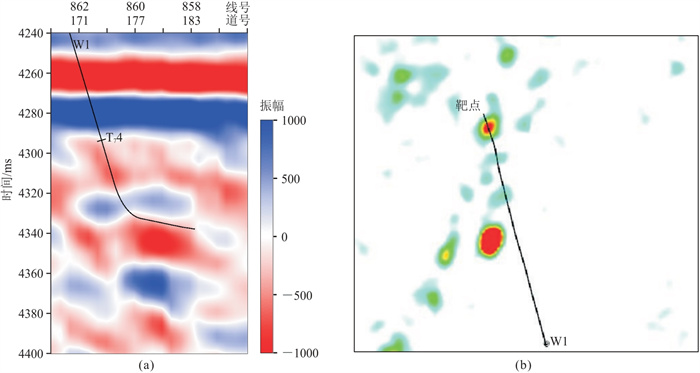
|
图 10 W1井特征 (a)过井地震剖面;(b)振幅属性平面图T74为奥陶系一间房组顶界面。 |
因此,开展基于叠前分频的缝洞体尺度预测、尺度校正、空间定位等工作,确定有利储集体与井轨迹之间的空间距离关系,为射孔位置确定、酸化压裂方案设计提供技术支撑。
3.2 分频尺度预测首先,利用原始CMP道集进行叠前分频处理。根据资料频谱特征,设置分频参数为6组,主频和带宽分别为10 Hz和4~15 Hz、15 Hz和10~20 Hz、20 Hz和15~25 Hz、25 Hz和20~30 Hz、30 Hz和25~35 Hz、40 Hz和30~50 Hz,频域滤波器镶边统一为5 Hz。分频成像结果如图 11所示,可以看到缝洞体在不同地震频带上的响应有差异。
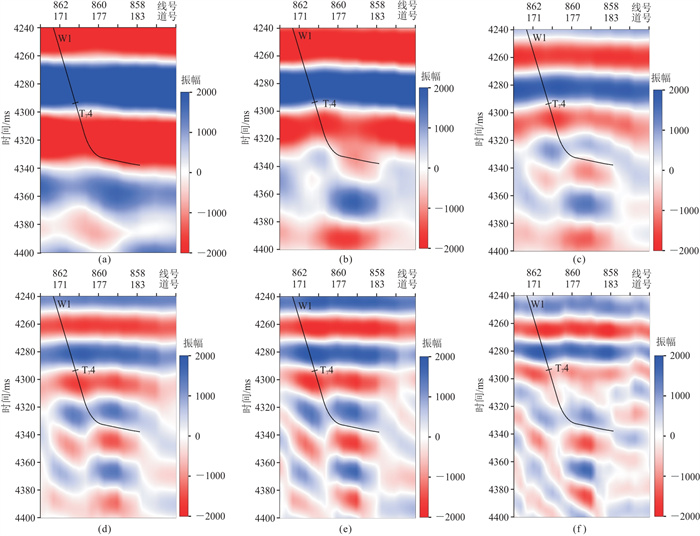
|
图 11 过W1井不同主频分频剖面 (a)10 Hz;(b)15 Hz;(c)20 Hz;(d)25 Hz;(e)30 Hz;(f)40 Hz。 |
提取过“串珠”位置响应波形(图 12),并提取波峰到波谷的相对振幅,基于高斯函数拟合方法计算调谐频率(图 13)。可知调谐频率为24.7 Hz,理论调谐厚度(围岩速度为6000 m/s)为60.7 m,时间厚度为20 ms左右。
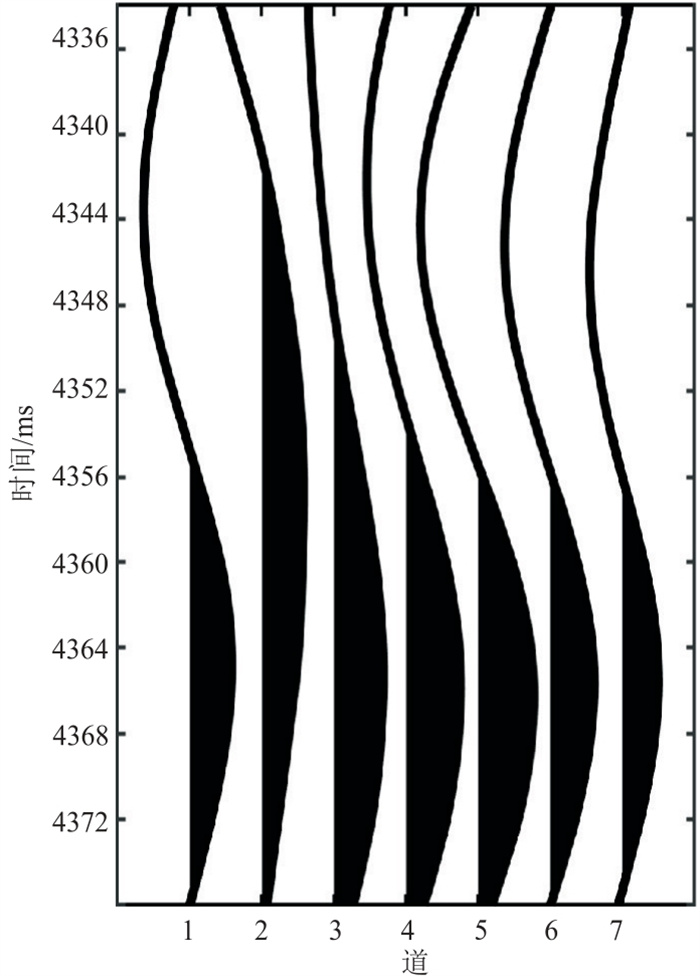
|
图 12 缝洞体位置分频波形曲线 从左向右,依次为全频带和主频15、23、30、35、40、50 Hz的波形。 |
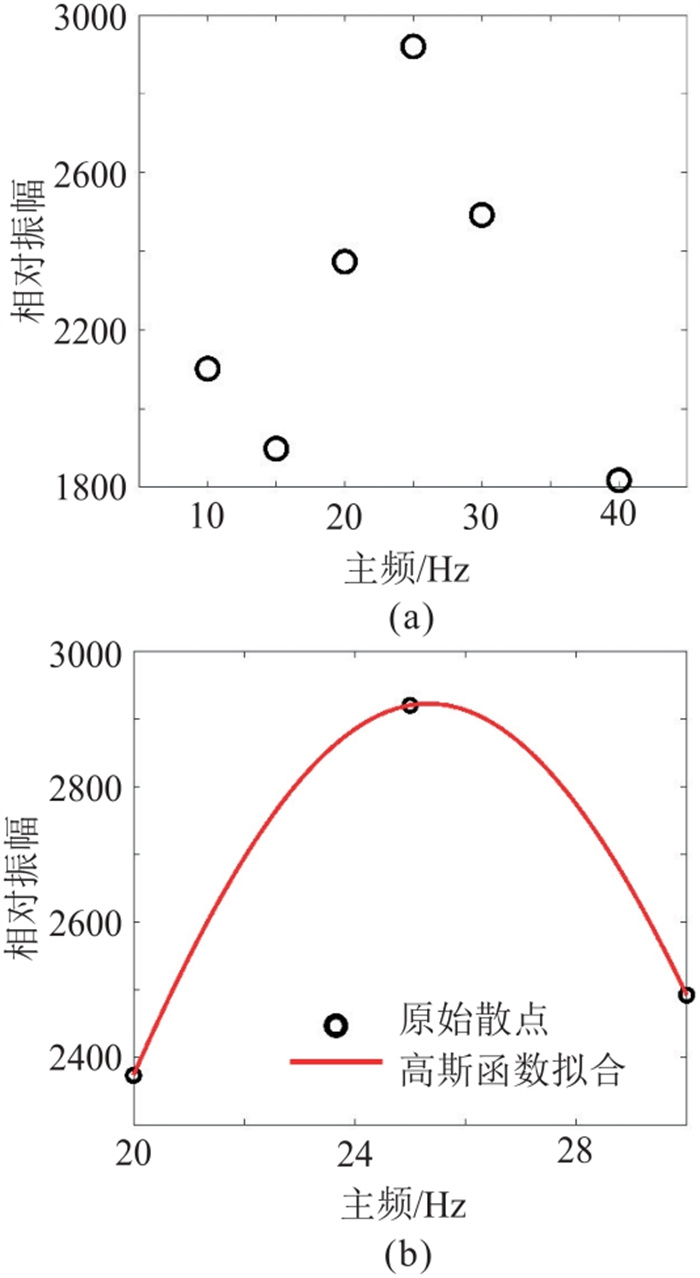
|
图 13 调谐频率计算 (a)原始散点图;(b)高斯函数拟合图 |
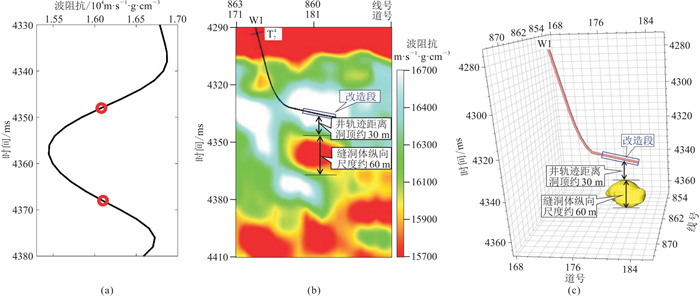
利用地震资料反演得到纵波阻抗数据体,提取“串珠”中心阻抗曲线(14a)。根据缝洞体尺度预测结果(“串珠”时间厚度为20 ms),对阻抗曲线阈值进行扫描。当阻抗阈值为1.610×104 m·s-1·g·cm-3时,低阻抗曲线段(缝洞体发育部位)满足缝洞体纵向时间厚度20 ms的条件,顶、底时间分别为4348、4368 ms,顶、底两点阻抗值分别为1.608×104、1.610×104 m·s-1·g·cm-3,此时缝洞体纵向尺度约为60 m。同时,计算井轨迹距缝洞体顶部最短为30 m左右,尺度预测和三维雕刻分别如图 14b和图 14c所示,即可实现缝洞体空间定位。根据缝洞体定量预测及空间定位成果,初步确定了改造段范围(图 14c中蓝框所示),根据预测的储集体量化特征及相关距离参数,针对下部缝洞体开展酸化压裂作业,设计了相应的压裂排量、方向、总量等关键参数。压裂效果显示各参数选择合理,储集体得到了沟通,试产日超百吨,效果明显。
|
图 14 过W1井缝洞体尺度预测结果 (a)阻抗阈值标定;(b)尺度预测;(c)空间定位 |
本文提出了基于分频尺度约束的缝洞体空间定位方法,理论分析、模型测试均验证了方法的可靠性,在实际资料应用中取得了显著的效果,具有较好的适用性。主要认识如下:
(1) 基于地震波调谐理论可以较好实现缝洞体尺度预测,理论上可行,模型测试也验证了其准确性,具有较好的可靠性和适用性;
(2) 采用高斯函数拟合方法可以对多个有限散点进行拟合,从而计算得到较为准确的调谐频率值,为缝洞体尺度精细预测奠定了良好基础;
(3) 基于分频尺度参数约束缝洞体阻抗阈值方法较好地实现了缝洞体尺度预测和空间定位,值得进一步推广应用。
需要指出的是,本文方法适用于孤立的、受其他地震反射层影响较小的缝洞体。当缝洞体受其他干扰(如强反射界面等)时,计算结果误差较大。这需要提前开展反射层分离等工作,突出缝洞体真实反射特征,再进行缝洞体尺度预测,可有效减小误差。
| [1] |
胡中平, 李宗杰, 赵群. 碳酸盐岩溶洞发育区高精度地震勘探效果[J]. 石油地球物理勘探, 2008, 43(1): 83-87. HU Zhongping, LI Zongjie, ZHAO Qun. High-precision seismic exploration in carbonate karst cave developed area[J]. Oil Geophysical Prospecting, 2008, 43(1): 83-87. |
| [2] |
云露. 顺北东部北东向走滑断裂体系控储控藏作用与突破意义[J]. 中国石油勘探, 2021, 26(3): 41-52. YUN Lu. Controlling effect of NE strike-slip fault system on reservoir development and hydrocarbon accumulation in the eastern Shunbei area and its geological significance, Tarim Basin[J]. China Petroleum Exploration, 2021, 26(3): 41-52. |
| [3] |
王彦峰, 王乃建, 高国成, 等. 缝洞型油气藏高精度三维地震采集技术[J]. 石油地球物理勘探, 2010, 45(增刊1): 1-5. WANG Yanfeng, WANG Naijian, GAO Guocheng, et al. 3D seismic acquisition technique for fracture-vuggy reservoir[J]. Oil Geophysical Prospecting, 2010, 45(S1): 1-5. |
| [4] |
张军华, 李军, 吴成, 等. 溶洞型储层地震采集参数与成像关系研究[J]. 石油地球物理勘探, 2015, 50(4): 573-579. ZHANG Junhua, LI Jun, WU Cheng, et al. The relationship between seismic acquisition parameters and data imaging in areas with cavern reservoirs[J]. Oil Geophysical Prospecting, 2015, 50(4): 573-579. |
| [5] |
魏建新, 狄帮让, 王立华. 孔洞储层地震物理模拟研究[J]. 石油物探, 2008, 47(2): 156-160. WEI Jianxin, DI Bangrang, WANG Lihua. Seismic physical modeling for cavern reservoir[J]. Geophysical Prospecting for Petroleum, 2008, 47(2): 156-160. |
| [6] |
朱生旺, 魏修成, 曲寿利, 等. 用随机介质模型方法描述孔洞型油气储层[J]. 地质学报, 2008, 82(3): 420-427. ZHU Shengwang, WEI Xiucheng, QU Shouli, et al. Description of the carbonate karst reservoir with random media model[J]. Acta Geologica Sinica, 2008, 82(3): 420-427. |
| [7] |
赵群, 曲寿利, 薛诗桂, 等. 碳酸盐岩溶洞物理模型地震响应特征研究[J]. 石油物探, 2010, 49(4): 351-358, 400. ZHAO Qun, QU Shouli, XUE Shigui, et al. Study on the seismic response characteristics on the physical model of carbonate cave[J]. Geophysical Prospecting for Petroleum, 2010, 49(4): 351-358, 400. |
| [8] |
李凡异, 魏建新, 狄帮让, 等. 碳酸盐岩孔洞储层地震物理模型研究[J]. 石油地球物理勘探, 2016, 51(2): 272-280. LI Fanyi, WEI Jianxin, DI Bangrang, et al. Seismic physical model of carbonate cavern reservoirs[J]. Oil Geophysical Prospecting, 2016, 51(2): 272-280. |
| [9] |
WU R S, AKI K. Scattering characteristics of elastic waves by an elastic heterogeneity[J]. Geophysics, 1985, 50(4): 582-595. |
| [10] |
胡鹏飞. 塔河油田碳酸盐岩缝洞型储集体成像技术研究[J]. 石油地球物理勘探, 2009, 44(2): 152-157. HU Pengfei. Study on imaging technique of carbonate fracture-cave type's reservoir in Tahe Oilfield[J]. Oil Geophysical Prospecting, 2009, 44(2): 152-157. |
| [11] |
LIU Y, WANG Y H. Seismic characterization of a carbonate reservoir in Tarim Basin[J]. Geophysics, 2017, 82(5): 177-188. |
| [12] |
刘春园, 魏修成, 朱生旺, 等. 频谱分解在碳酸盐岩储层中的应用研究[J]. 地质学报, 2008, 82(3): 428-432. LIU Chunyuan, WEI Xiucheng, ZHU Shengwang, et al. Application of spectral decomposition in carbonate reservoir[J]. Acta Geologica Sinica, 2008, 82(3): 428-432. |
| [13] |
WANG S X, GUAN L P, ZHU H L. Prediction of fracture-cavity system in carbonate reservoir: a case study in the Tahe Oilfield[J]. Applied Geophysics, 2004, 1(1): 28-31. |
| [14] |
常少英, 曾溅辉, 徐旭辉, 等. 碳酸盐岩断溶体内部结构识别技术及应用[J]. 石油地球物理勘探, 2022, 57(2): 414-422. CHANG Shaoying, ZENG Jianhui, XU Xuhui, et al. Identification technology for internal structures of carbonate fault-karst and its application[J]. Oil Geophysical Prospecting, 2022, 57(2): 414-422. |
| [15] |
张傲, 李宗杰, 刘军, 等. 基于Yolox算法的碳酸盐岩储层溶洞"串珠状"异常反射智能检测[J]. 石油地球物理勘探, 2023, 58(3): 540-549. ZHANG Ao, LI Zongjie, LIU Jun, et al. Intelligent detection of "bead-shaped" abnormal reflections in carbonate reservoir caves based on Yolox algorithm[J]. Oil Geophysical Prospecting, 2023, 58(3): 540-549. |
| [16] |
ZHU B H, YANG J F, SUN Z T, et al. Multi-scale cave detection based on amplitude difference of pre-stack frequency division data volumes[C]. 80th EAGE Conference and Exhibition, 2018, 1-5.
|
| [17] |
朱博华, 杨江峰, 吕秋玲, 等. 基于分频成像的小尺度溶洞检测[J]. 石油地球物理勘探, 2018, 53(3): 538-544. ZHU Bohua, YANG Jiangfeng, LYU Qiuling, et al. Small‑scale cave detection based on frequency-segmented imaging[J]. Oil Geophysical Prospecting, 2018, 53(3): 538-544. |
| [18] |
杨江峰, 吕秋玲, 丁建强, 等. 分频叠前深度偏移技术在小尺度缝洞体成像中的应用[J]. 石油物探, 2021, 60(3): 488-495. YANG Jiangfeng, LYU Qiuling, DING Jianqiang, et al. Application of frequency-division prestack depth migration for the imaging of small-scale fracture-cavity reservoirs[J]. Geophysical Prospecting for Petroleum, 2021, 60(3): 488-495. |
| [19] |
徐旺林, 张繁昌, 郭彦如, 等. 贝叶斯全频信息同时反演在鄂尔多斯盆地碳酸盐岩储层预测中的应用[J]. 石油地球物理勘探, 2014, 49(4): 723-728. XU Wangling, ZHANG Fanchang, GUO Yanru, et al. Bayesian full frequency simultaneous inversion for carbonate reservoir in Erdos Basin[J]. Oil Geophysical Prospecting, 2014, 49(4): 723-728. |
| [20] |
陈军, 张虎权, 王锦喜, 等. AVO技术在碳酸盐岩缝洞型储层预测中的应用[J]. 石油地球物理勘探, 2014, 49(6): 1191-1198. CHEN Jun, ZHANG Huquan, WANG Jinxi, et al. Carbonate fracture‑cave reservoir prediction with prestack AVO[J]. Oil Geophysical Prospecting, 2014, 49(6): 1191-1198. |
| [21] |
WIDESS M B. How thin is a thin bed?[J]. Geophysics, 1973, 38(6): 1176-1180. |
| [22] |
曲寿利, 朱生旺, 赵群, 等. 碳酸盐岩孔洞型储集体地震反射特征分析[J]. 地球物理学报, 2012, 55(6): 2053-2061. QU Shouli, ZHU Shengwang, ZHAO Qun, et al. Analysis of seismic reflection characters for carbonate Karst reservoir[J]. Chinese Journal of Geophysics, 2012, 55(6): 2053-2061. |
| [23] |
李振春, 张军华. 地震数据处理方法[M]. 山东东营: 中国石油大学出版社, 2006. LI Zhenchun, ZHANG Junhua. Seismic Data Processing Method[M]. Dongying, Shandong: China University of Petroleum Press, 2006. |
| [24] |
马英杰, 周靖, 洪旭, 等. 核能谱单能峰快速高精度高斯函数拟合算法研究[J]. 光谱学与光谱分析, 2016, 36(8): 2373-2377. MA Yingjie, ZHOU Jing, HONG Xu, et al. Study on the high speed and precision Gaussian function fitting algorithm for nuclear single spectral peak[J]. Spectroscopy and Spectral Analysis, 2016, 36(8): 2373-2377. |



 王洋, 江苏省南京市江宁区上高路219号中石化石油物探技术研究院有限公司,211103。Email:
王洋, 江苏省南京市江宁区上高路219号中石化石油物探技术研究院有限公司,211103。Email: