2. 中国石油集团测井有限公司, 陕西西安 710077
2. China National Logging Corporation, Xi'an, Shaanxi 710077, China
随钻电磁波测井(Logging-while-drilling,LWD)技术广泛应用于油气勘探领域,对大斜度井或水平井的测量至关重要[1-3]。正则化反演是一种非线性多参数的反演方法,可以基于梯度下降法和线性化理论,将反演问题线性化,使其更容易求解[4-5]。王磊等[6]使用随钻方位电磁波测井技术对一系列一维模型进行反演,利用最优化算法对现场资料进行处理,取得了良好的应用效果。张国华等[7]提出了水平井和大斜度井多界面三维电阻率反演方法,准确获取了水平井和大斜度井地层电阻率剖面和井眼地层的位置关系。Thiel等[8]利用高斯—牛顿法确定了一维各向异性地层的电阻率剖面和倾角,实现了电阻率模型的高分辨率成像。这些方法均是通过迭代方式不断减少预测数据与真实数据之间的误差。由于迭代过程中需要多次调用正演程序,计算耗时长,且不能实时获得反演结果[9-10],因此迫切需要一种高效的反演方法对随钻电磁波测井资料进行实时反演。
近年来,越来越多的学者利用深度学习算法求解随钻电磁波测井反演问题[11-13]。传统深度学习的反演方法在数据和模型之间建立了复杂的非线性关系,从而构造一个从输入到输出的复杂非线性映射,避免了与线性化相关的大量计算问题[14]。虽然训练过程比较耗时,但是当网络训练成功后,反演的效率和精度将显著提高[13]。康正明等[15]提出了一种基于长短期记忆人工神经网络(LSTM)的反演方法,用于求取地层电阻率。Noh等[16]针对强、弱噪声的影响,开发了一种深度反演流程,使用合成电阻率模型测试三种存在明确噪声的反演网络,网络的鲁棒性显著增强。Noh等[17]针对包含断层的二维各向异性地层模型,使用短LWD和超深LWD装置的正演数据进行深度学习反演,以此推断测井轨迹周围电阻率的空间分布。然而,随着网络深度的增加,网络的学习能力会有所下降[14]。
在深度学习反演过程中,损失函数的设计对于防止学习能力下降等问题尤为重要。Shahriari等[18]提出了一种具有高权值惩罚项的损失函数,通过平滑函数提升反演性能。
由于单一的深度学习反演方法是纯数据驱动的,网络性能大都取决于样本数据集,传统神经网络的权值等参数不能准确反映声波、电磁波等物理性质,导致反演效果不佳。因此,在网络模型中加入物理项可以更好地适应电磁场特征,从而提高反演效果。Colombo等[19]将物理约束项和数据残差项等物理属性嵌入电磁框架中的深度神经网络,以此提高模型的精度。Liu等[20]将大地电磁波的物理特征整合到纯数据驱动的反演中,建立了物理驱动的反演工作流程,模拟得到的响应与实际测量结果一致。本文将这种物理驱动的方法应用到超深随钻方位电磁波测井领域,通过正演计算为反演过程提供理论约束,减少神经网络对训练数据集的依赖,从而提升反演效果,实现实时反演。
本文针对一个包含倾斜层和断层的二维各向异性地层,提出了一种耦合数据驱动和物理驱动的混合反演流程:基于超深随钻方位电磁波测井数据,随机生成无断层模型和断层模型数据集进行网络训练;基于训练好的网络,进行模型反演预测。通过与传统深度学习反演结果对比,评估分析基于物理驱动的深度学习方法的反演效果。
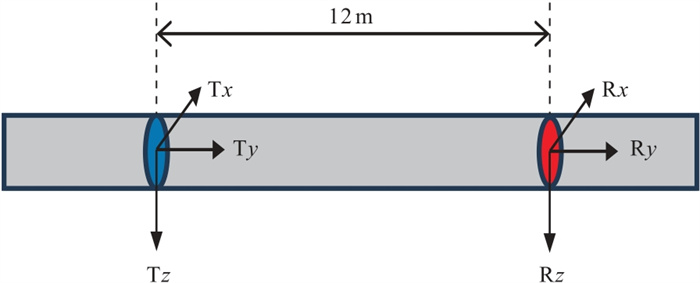
1 超深随钻方位电磁波观测系统超深随钻方位电磁波测井通过增大源距、降低发射频率来增加探测深度。超深随钻方位电磁波测井仪器的发射源和接收机的布局如图 1所示。
|
图 1 超深随钻方位电磁波测井发射源和接收机分布示意图 |
超深随钻方位电磁波测井仪器由一个发射源T和一个接收机R组成,收发装置由三个相互正交的发射线圈(Tx、Ty、Tz)和接收线圈(Rx、Ry、Rz)组成,其输出的测量数据包括发射源和接收机所有可能的方向组合:
假设发射源沿z方向,以z耦合磁场分量
| $ \mathrm{A}\mathrm{t}\mathrm{t}=\mathrm{l}\mathrm{n}\frac{\left|{H}_{zz}-{H}_{zx}\right|}{\left|{H}_{zz}+{H}_{zx}\right|} $ | (1) |
预处理后的相位差可表示为
| $ \mathrm{P}\mathrm{s}=\mathrm{p}\mathrm{h}({H}_{zz}-{H}_{zx})-\mathrm{p}\mathrm{h}({H}_{zz}+{H}_{zx}) $ | (2) |
式中ph表示求取相位。利用式(1)和式(2)可以计算模型的振幅比和相位差,并将其作为深度神经网络的输入。
2 基于物理驱动的深度学习反演的原理针对随钻电磁波测井地下反演成像问题,耦合物理驱动与深度学习的方法有三种[24]:
(1) 对数据施加约束,将先验信息作为输入的一部分进行网络训练;
(2) 在神经网络中添加自定义的物理层;
(3) 对损失函数施加约束,将先验物理信息作为损失函数中的正则化项,对函数进行约束。
本文在损失函数中加入模型约束项以及数据残差项,将输入数据和输出模型的物理特性嵌入损失函数。基于物理驱动的深度学习反演方法的损失函数设计如图 2所示。

|
图 2 基于物理驱动的深度学习反演方法的损失函数设计 |
LWD反演方法通过模型向量
| $ \begin{array}{l}{ϕ }_{d}\left(\boldsymbol{m}\right)=(\boldsymbol{G}\boldsymbol{m}-{\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}{)}^{\mathrm{T}}{\boldsymbol{W}}_{d}^{\mathrm{T}}{\boldsymbol{W}}_{d}(\boldsymbol{G}\boldsymbol{m}-{\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}})\\ =\left|\right|{\boldsymbol{W}}_{d}(\boldsymbol{G}\boldsymbol{m}-{\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}})|{|}_{{\mathrm{L}}_{2}}^{2}\end{array} $ | (3) |
式中:
深度学习反演过程中,使用观测数据向量的正演响应
| $ {\boldsymbol{m}}_{\mathrm{p}}=H({\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}};\theta ) $ | (4) |
式中:
| $ {ϕ }_{\mathrm{L}, \boldsymbol{m}}\left(\theta \right)=\left|\right|H({\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}};\theta )-{\boldsymbol{m}}_{\mathrm{t}}|{|}_{{\mathrm{L}}_{2}}^{2} $ | (5) |
将基于物理驱动的深度学习反演方法的损失函数定义为
| $ ϕ (\boldsymbol{m}, \theta )={ϕ }_{\boldsymbol{d}}\left(\boldsymbol{m}\right)+{\mu }_{1}{ϕ }_{\mathrm{L}, \boldsymbol{m}}\left(\theta \right)+{\mu }_{2}{ϕ }_{\boldsymbol{m}}\left(\boldsymbol{m}\right) $ | (6) |
式中:
| $ {ϕ }_{\boldsymbol{m}}\left(\boldsymbol{m}\right)=\sum\limits_{i=2}^{N}\left[{\boldsymbol{m}}_{\mathrm{p}}^{(i-1)}+{\boldsymbol{m}}_{\mathrm{p}}^{(i+1)}-2{\boldsymbol{m}}_{\mathrm{p}}^{\left(i\right)}\right] $ | (7) |
式中:i代表当前迭代次数;N为模型总个数。
随着网络参数
| $ {\theta }^{\left(i\right)}=\underset{\theta }{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\left|\right|\boldsymbol{H}({\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}};\theta )-{\boldsymbol{m}}_{\mathrm{t}}\left)\right|{|}_{{\mathrm{L}}_{2}}^{2} $ | (8) |
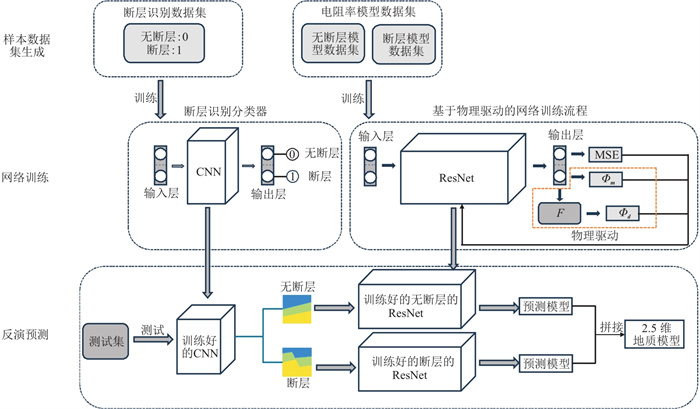
基于物理驱动的深度学习反演工作流程包括三个部分:生成样本数据集,网络训练和反演预测(图 3)。
|
图 3 基于物理驱动的深度学习反演工作流程图 |
第一部分是样本数据集的生成。本文使用三层各向异性地层(包含倾斜层和断层)模型生成样本数据集。第一种类型为基于断层识别的数据集,用于反演预测前的模型分类。第二种类型为两个独立的电阻率模型数据集:无断层模型和断层模型,用于反演网络的训练,具体细节在第4节中介绍。
第二部分是网络训练。本文引入卷积神经网络(Convolutional Neural Network,CNN)确定模型中是否存在断层面。使用交叉熵函数和sigmoid激活函数构造CNN的目标函数。交叉熵函数表达式为
| $ \mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}=\frac{1}{N}\sum\limits_{i=0}^{N}-[{y}_{i}\mathrm{l}\mathrm{g}{p}_{i}+(1-{y}_{i})\mathrm{l}\mathrm{g}(1-{p}_{i})] $ | (9) |
式中:
| $ S\left(x\right)=1/(1+{\mathrm{e}}^{-x}) $ | (10) |
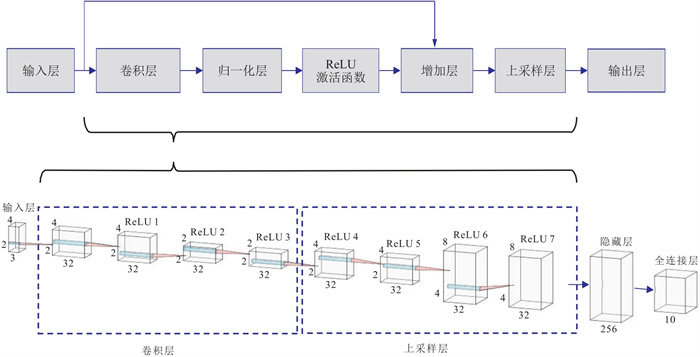
本文使用残差网络(ResNet)对断层和无断层电阻率模型进行网络训练(图 4)。网络共有29层,即:3 (卷积层,归一化层,ReLU激活函数层)
|
图 4 ResNet结构及训练流程 |
对于每一个地层模型,正演数据包含12(测井点)
本文采用均方误差(Mean Square Error,MSE)作为损失函数优化网络训练。利用预测模型与实际模型的正演响应的差值计算数据残差,将残差数据作为损失函数的一部分,并对其增加模型约束。最终的损失函数由MSE、模型约束和数据残差组成。将电阻率模型数据集输入ResNet结构进行训练,通过最小化损失函数可以得到训练好的神经网络。
第三部分是反演预测。将测试模型输入训练好的CNN网络进行断层识别。基于识别结果,将两种测试集分别输入对应的两个训练好的神经网络,可输出模型预测结果。
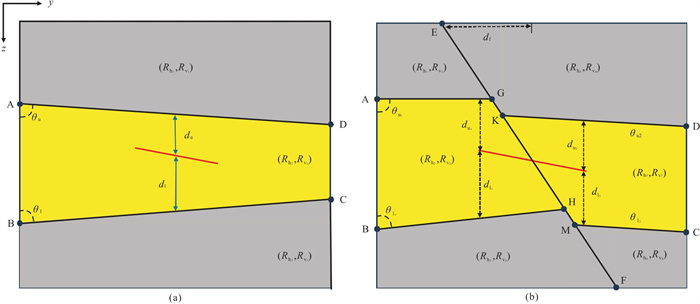
4 数据集设计 4.1 断层识别数据集设计为了进行断层识别,需要构造一个样本数据集来解决二元分类问题。本文生成了两种模型,一种是无断层模型(图 5a),另一种是断层模型(图 5b)。水平方向上,断层位于发射源和接收机之间。
|
图 5 无断层和断层模型的参数图
(a) 无断层模型;(b)断层模型。图中红线表示二维测井轨迹在y方向上的投影。图a中, |
首先,分析图 5a中的无断层模型。二维模型位于yOz面上,地层的水平电阻率变化范围为[0.1 Ω·m, 100.0 Ω·m],各向异性系数变化范围为[1, 100]。
然后,分析图 5b中的断层模型,该模型的参数
在实际建模过程中,可以将多个地层参数的变化转化为不同动点的设置[30]。基于图 5a中的无断层模型,将10个变量转化为四个动点(A、B、C、D)的坐标;基于图 5b中的断层模型,将22个变量转化为10个动点(A、B、C、D、E、F、G、H、K、M)的坐标。通过控制动点的变化,连接相应的动点可以构建相应的地层模型。计算其振幅和相位,通过预处理可以得到振幅比数据集和相位差数据集。训练过程中,用“1”表示模型中存在断层,用“0”表示模型中不存在断层,对模型赋予对应的标签。以振幅比Att和相位差Ps作为输入,标签值(0或1)作为输出,基于开源的深度学习软件库TensorFlow进行网络训练。
4.2 电阻率模型数据集设计将模型的振幅比和相位差作为输入,电阻率模型的参数作为输出,设计电阻率模型数据集。模型参数为无断层模型的10个参数和断层模型的22个参数。为了克服模型间电阻率差异过大的影响,使电阻率具有可比性,对电阻率取对数。由反演参数可以得到对应的动点和电阻率值,通过连接各个动点得到对应的模型边界,根据边界电阻率可以得到对应的模型。
本节生成两个独立的数据集:无断层模型和断层模型。分别模拟这两个模型,得到50000个样本,其中90%的样本用于训练,10%的样本用于验证。基于TensorFlow训练深度神经网络,使用Adam算法对网络进行优化,将学习率设置为
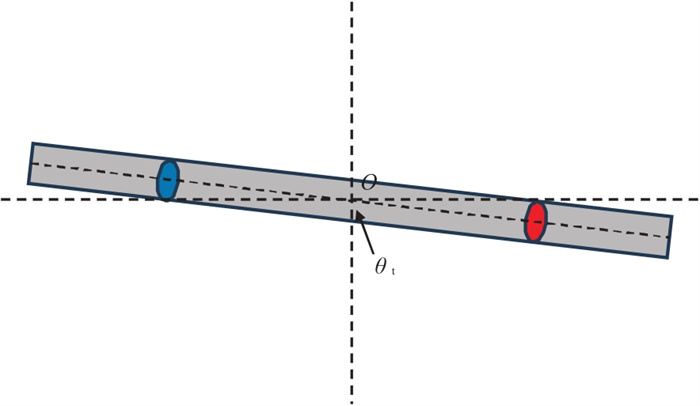
本文将发射源与接收机的间距设置为12 m,工作频率设置为10k Hz。实际测量中,测井装置需要实时偏移,以保证测量数据的准确性。如图 6所示,设置测井轨迹倾角
|
图 6 超深随钻方位电磁波测井仪器实时更新示意图 |
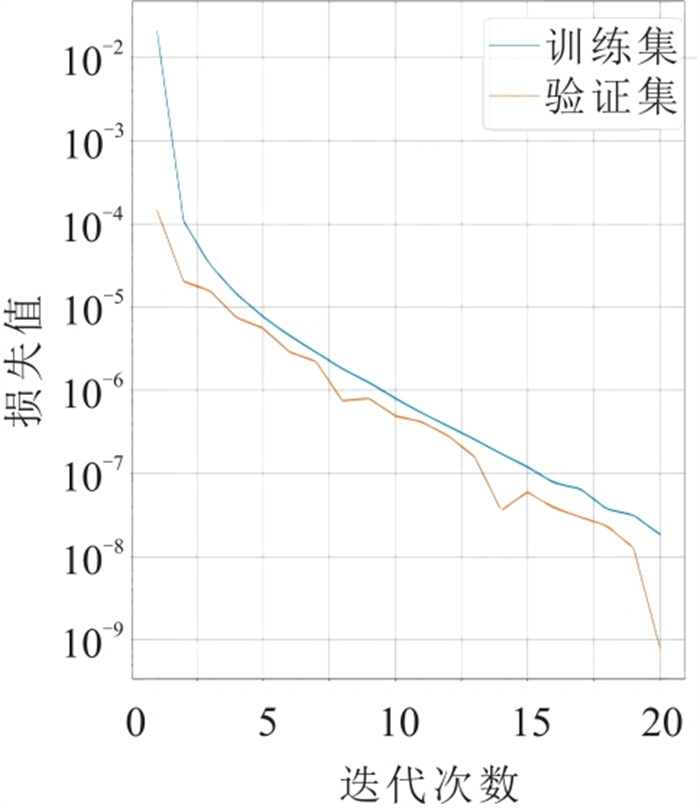
首先训练了一个断层识别网络,据此对反演前的断层进行分类。图 7为断层识别网络在训练集和验证集上的损失函数曲线,可见经过20次连续迭代训练,损失值降至约1×10-7,训练集和验证集曲线趋势基本一致。
|
图 7 断层识别网络在训练集和验证集上的损失函数曲线 |
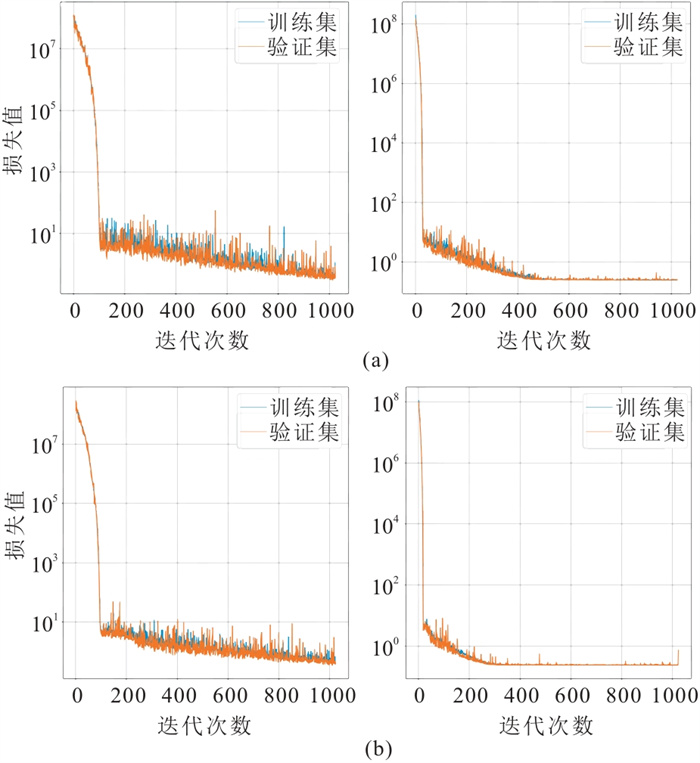
传统深度学习和基于物理驱动的深度学习反演方法的损失值见图 8,可见经过1024次迭代训练,损失值基本趋于稳定。可以直观地看出基于物理驱动的深度学习反演获得了更好的拟合度,训练集和验证集的损失值更小,曲线形态更加一致,迭代1024次后损失函数值基本趋于稳定。
|
图 8 基于传统深度学习(左)和物理驱动深度学习(右)反演方法在训练集和验证集的损失函数曲线 (a)无断层模型;(b)断层模型 |
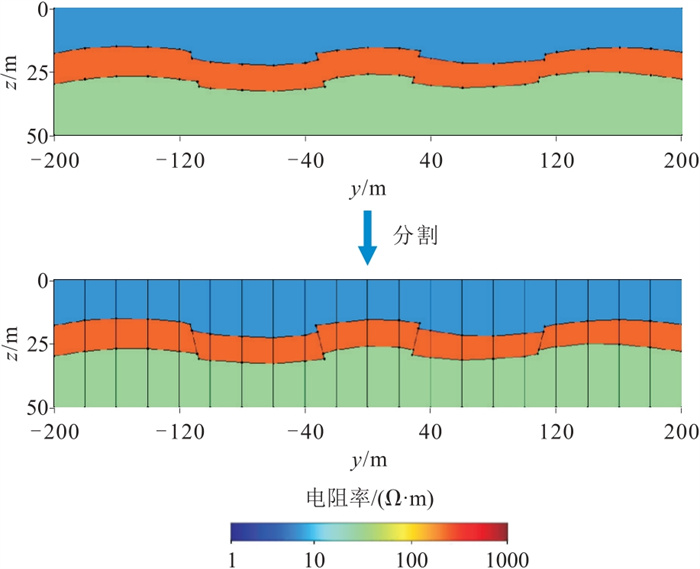
沿着测井轨迹,构建一个包含两个倾斜断层的二维各向异性地层。对水平和垂直电阻率取对数,设置上层电阻率为
|
图 9 包含断层的二维电阻率各向异性地层(上)及等距分割图(下) |
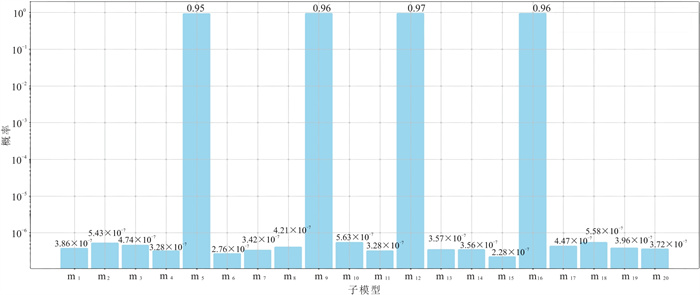
将图 9中分割后的20个子模型从左至右顺序命名为m1~m20,并将其输入训练好的CNN中进行断层识别。这20个测试模型中存在断层的概率如图 10所示,可以看出m5、m9、m12和m16子模型中存在断层的概率(接近于1)明显高于其他子模型,说明这4个子模型中包含断层,而其他子模型不包含断层,与图 9一致。据此,将无断层模型和断层模型的正演响应输入训练好的网络中进行测试,可以得到对应模型的电阻率预测结果。
|
图 10 图 9子模型中存在断层的概率分布 |
基于传统深度学习和物理驱动的深度学习反演方法得到的二维各向异性地层预测结果见图 11,可见与传统深度学习方法的反演结果相比,基于物理驱动的深度学习反演方法的预测模型的边界与真实模型的边界拟合效果更好,在断层位置和地层剧烈起伏层位置,边界拟合效果更佳,即模型重建效果更好。

|
图 11 图 9模型不同方法反演结果对比 |
为了分析、测试各个参数的预测值与真实值的相对误差,进一步使用回归问题中的相关系数R2和正则化反演中的均方根(Root Mean Square,RMS)对反演结果进行评估。
相关系数R2通常用于评价回归问题中的预测结果[31],其表达式为
| $ \begin{array}{l}{R}^{2}=1-\mathrm{S}\mathrm{S}\mathrm{E}/\mathrm{S}\mathrm{S}\mathrm{T}\\ =1-\sum ({m}_{\mathrm{t}}-{m}_{\mathrm{p}}{)}^{2}/\sum ({m}_{\mathrm{t}}{-\stackrel{-}{m})}^{2}\end{array} $ | (11) |
式中:
均方根RMS又叫最小拟合差,用于表征反演的拟合程度。当RMS接近1时,表明与最小二乘法的反演拟合基本一致,此时达到拟合要求。其表达式为
| $ \mathrm{R}\mathrm{M}\mathrm{S}=\sqrt{\frac{1}{N}\sum\limits_{i=1}^{N}({m}_{\mathrm{p}, i}-{m}_{\mathrm{t}, i}{)}^{2}} $ | (12) |
式中:
首先,随机生成100个无断层模型和断层模型作为验证集,分别输入对应的训练好的两种深度学习反演网络进行预测。然后,以反演后的每个验证集的实际电阻率参数为横坐标,以预测电阻率参数为纵坐标,绘制各模型的散点图。通过比较散点与
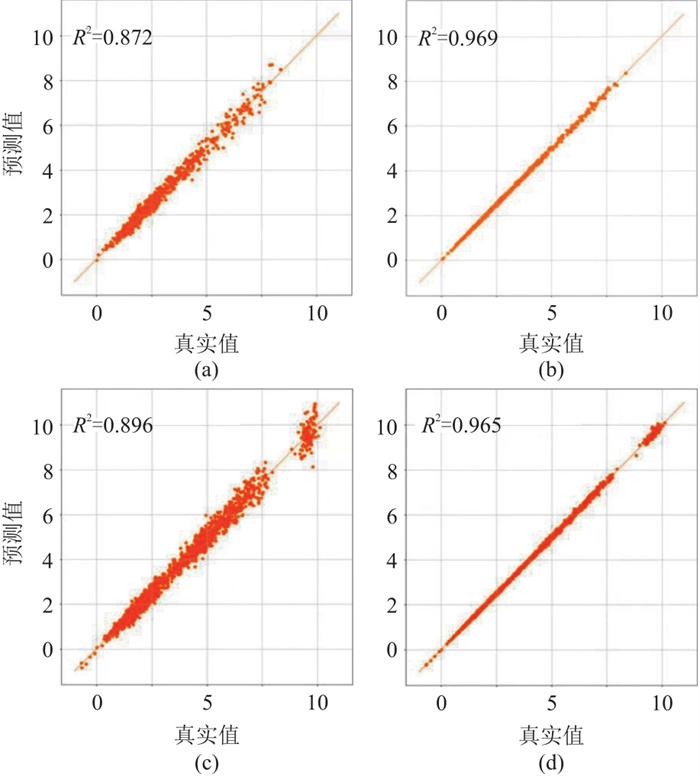
分别基于传统深度学习和物理驱动深度学习的反演方法的验证集误差评估结果如图 12所示。对比传统深度学习网络,基于物理驱动的深度学习网络预测结果精度显著提升,
|
图 12 基于传统深度学习和物理驱动深度学习反演方法的验证集误差估计 (a) 基于传统深度学习网络的无断层模型;(b)基于物理驱动学习反演的无断层模型;(c)基于传统深度学习网络的断层模型;(d)基于物理驱动深度学习反演的断层模型 |
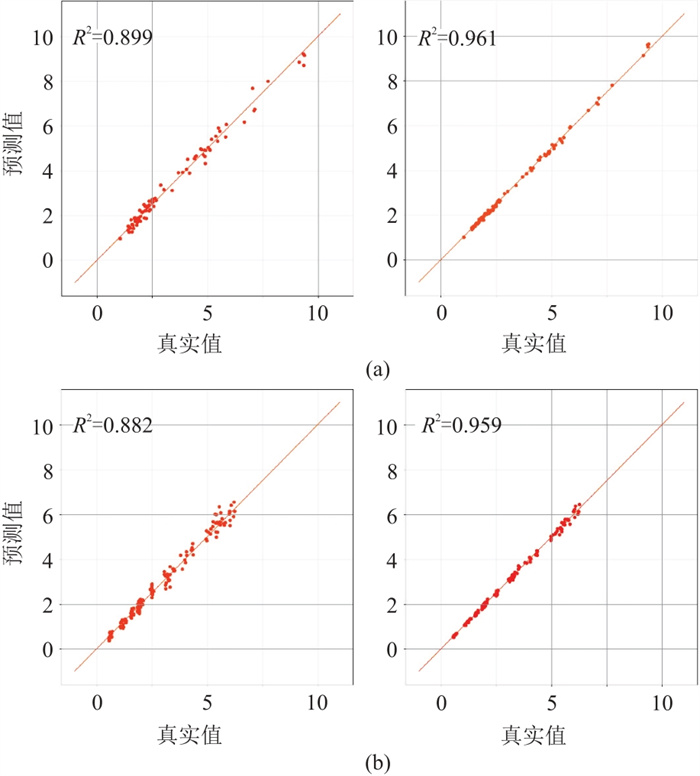
基于图 10所示的断层识别结果,将无断层模型和断层模型的正演响应输入训练好的网络进行测试,将测试结果代入式(11)进行误差估计,测试集误差估计结果见图 13。与传统深度学习的方法相比,基于物理驱动的深度学习反演方法的
|
图 13 基于传统深度学习(左)和物理驱动深度学习(右)的测试集误差估计统计 (a)断层模型;(b)无断层模型 |
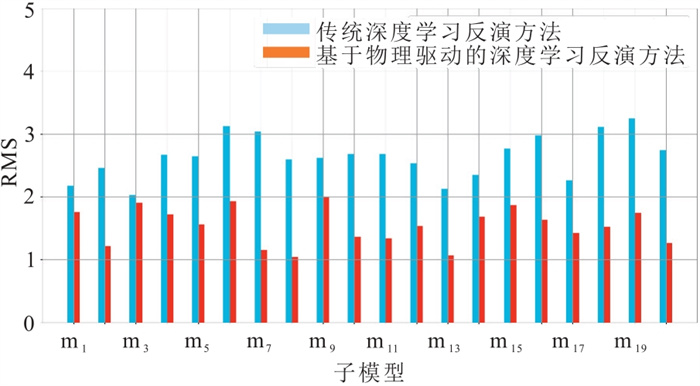
将传统深度学习和物理驱动深度学习神经网络预测模型的实际值和预测值分别代入式(12),得到相应的RMS(图 14),可见基于传统深度学习反演结果的RMS明显高于基于物理驱动的深度学习反演结果,且后者的RMS更接近1,表明基于物理驱动的深度学习反演效果更优。
|
图 14 基于传统深度学习和物理驱动深度学习反演方法的测试集RMS统计 |
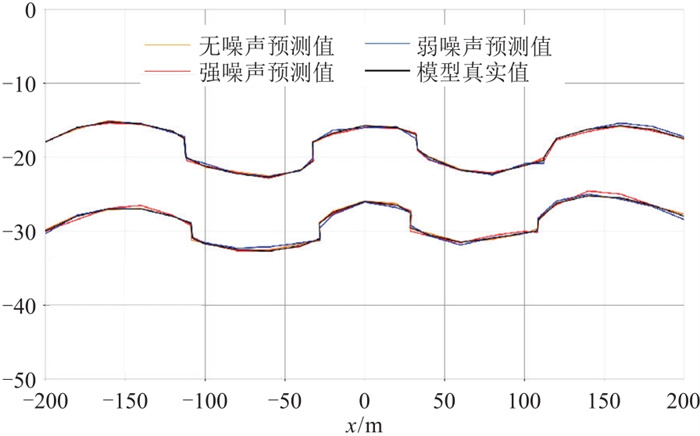
在测试集中加入不同程度的噪声,分析基于物理驱动的深度学习反演网络的鲁棒性。对测试集的振幅比和相位差分别添加弱噪声(
|
图 15 添加噪声测试模型的反演预测模型对比 |
由图 15可以看出,即便存在噪声的影响,模型起伏趋势依然与真实模型一致,边界较吻合。用随机生成的100个无断层模型和断层模型作为验证集进一步预测,其误差估计如图 16所示。
|
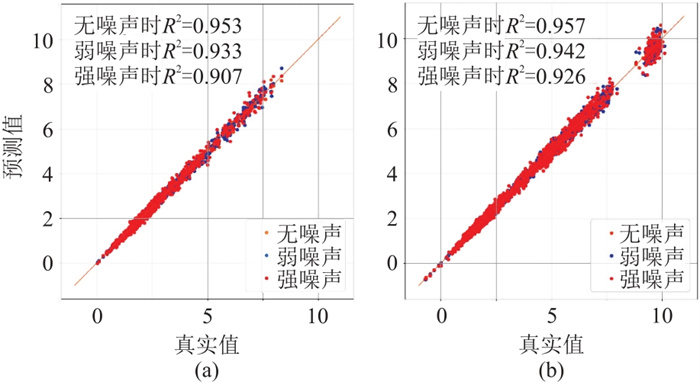
图 16 基于物理驱动的深度学习反演模型噪声验证集交会图 (a)无断层模型;(b)断层模型 |
由图 16可以看出,即便添加了强噪声,验证集的R2仍达到0.9以上,说明基于物理驱动的深度学习反演网络具有较强的稳定性。
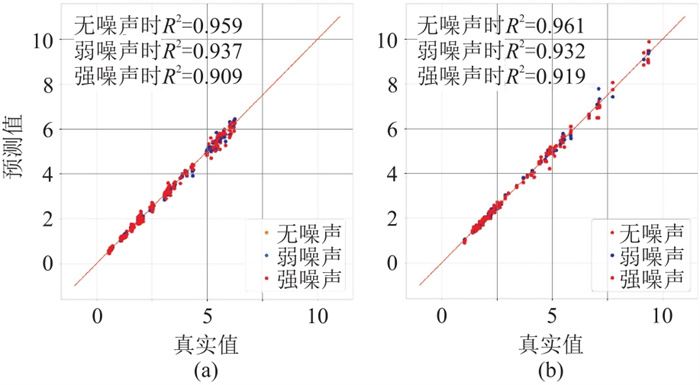
参照前文,用同样的方法对测试集添加噪声,其误差估计如图 17所示。可以看出,测试算例的R2同样保持在0.9以上,证明基于物理驱动的深度学习反演网络的鲁棒性较强。
|
图 17 基于物理驱动的深度学习反演模型噪声测试集交会图 (a)无断层模型;(b)断层模型 |
本文提出了一种耦合物理驱动和数据驱动的混合反演流程,目的是解决超深随钻方位电磁波测井资料实时反演问题。针对二维各向异性地层,对比了基于传统深度学习和基于物理驱动的深度学习反演方法的预测结果,后者预测结果的R2更接近1,RMS值也更小,说明其预测精度更高,效果更好。对于加入了强噪声的数据,基于物理驱动的深度学习反演方法预测结果的R2仍保持在0.9以上,RMS亦可控制在较小范围内,重建后的电阻率模型边界清晰,表明基于物理驱动的深度学习反演网络具有较强的鲁棒性,泛化能力较强。
| [1] |
王磊, 刘英明, 王才志, 等. 水平井随钻电磁波测井实时正反演方法[J]. 石油勘探与开发, 2021, 48(1): 139-147. WANG Lei, LIU Yingming, WANG Caizhi, et al. Real - time forward modeling and inversion of logging -while - drilling electromagnetic measurements in hori-zontal wells[J]. Petroleum Exploration and Develop-ment, 2021, 48(1): 139-147. |
| [2] |
夏文鹤, 韩玉娇, 郭全兴, 等. 融合裂缝形态信息的电阻率测井成像图空白条带填充方法[J]. 石油地球物理勘探, 2024, 59(3): 533-542. XIA Wenhe, HAN Yujiao, GUO Quanxing, et al. A filling method of blank strip for electrical logging images based on morphological information of fractures[J]. Oil Geophysical Prospecting, 2024, 59(3): 533-542. |
| [3] |
韩波, 刘家琦. 多层电磁波测井反演[J]. 地球物理学报, 1998, 41(3): 416-423. HAN Bo, LIU Jiaqi. Multilayer inversion for electromagnetic wave logging[J]. Chinese Journal of Geophysics, 1998, 41(3): 416-423. |
| [4] |
程三, 张志勇, 周峰, 等. 非结构化网格渐进自适应正则化反演算法[J]. 石油地球物理勘探, 2022, 57(2): 467-477. CHENG San, ZHANG Zhiyong, ZHOU Feng, et al. Study on step-by-step regularization inversion based on adaptive unstructured mesh[J]. Oil Geophysical Prospecting, 2022, 57(2): 467-477. |
| [5] |
朱培民, 王家映, 詹正彬, 等. 随机共轭梯度反演法[J]. 石油地球物理勘探, 2000, 35(2): 208-213. ZHU Peimin, WANG Jiaying, ZHAN Zhengbin, et al. Stochastic conjugate gradient inversion[J]. Oil Geophysical Prospecting, 2000, 35(2): 208-213. |
| [6] |
王磊, 范宜仁, 袁超, 等. 随钻方位电磁波测井反演模型选取及适用性[J]. 石油勘探与开发, 2018, 45(5): 914-922. WANG Lei, FAN Yiren, YUAN Chao, et al. Selection criteria and feasibility of the inversion model for azimuthal electromagnetic logging while drilling (LWD)[J]. Petroleum Exploration and Development, 2018, 45(5): 914-922. |
| [7] |
张国华, 张伟, 吴意明, 等. 随钻方位电磁波测井反演方法研究及在水平井中的应用[J]. 地球物理学进展, 2017, 32(2): 927-938. ZHANG Guohua, ZHANG Wei, WU Yiming, et al. Inversion methods study of azimuthal EM LWD tool and its applications in horizontal well[J]. Progress in Geophysics, 2017, 32(2): 927-938. |
| [8] |
THIEL M, OMERAGIC D. High-Fidelity Real-Time imaging with electromagnetic Logging-While-Drilling measurements[J]. IEEE Transactions on Computational Imaging, 2017, 3(2): 369-378. |
| [9] |
REGIŃSKA T. A regularization parameter in discrete Ill-Posed problems[J]. SIAM Journal on Scientific Computing, 1996, 17(3): 740-749. |
| [10] |
ESSER E, GUASCH L, VAN LEEUWEN T, et al. Total variation regularization strategies in full-waveform inversion[J]. SIAM Journal on Imaging Sciences, 2018, 11(1): 376-406. |
| [11] |
吴易智, 范宜仁, 巫振观, 等. 基于卷积神经网络和MPGA-LM算法的阵列侧向测井快速反演方法[J]. 地球物理学报, 2021, 64(9): 3410-3425. WU Yizhi, FAN Yiren, WU Zhenguan, et al. A fast inversion method for array laterolog based on convolutional neural network and hybrid MPGA-LM algorithm[J]. Chinese Journal of Geophysics, 2021, 64(9): 3410-3425. |
| [12] |
LIU B, GUO Q, LI S, et al. Deep learning inversion of electrical resistivity data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(8): 5715-5728. |
| [13] |
SHAHRIARI M, PARDO D, PICON A, et al. A deep learning approach to the inversion of borehole resistivity measurements[J]. Computational Geosciences, 2020, 24(3): 971-994. |
| [14] |
PUZYREV V. Deep learning electromagnetic inversion with convolutional neural networks[J]. Geophysical Journal International, 2019, 218(2): 817-832. |
| [15] |
康正明, 秦浩杰, 张意, 等. 基于LSTM神经网络的随钻方位电磁波测井数据反演[J]. 石油钻探技术, 2023, 51(2): 116-124. KANG Zhengming, QIN Haojie, ZHANG Yi, et al. Data inversion of azimuthal electromagnetic wave logging while drilling based on LSTM neural network[J]. Petroleum Drilling Techniques, 2023, 51(2): 116-124. |
| [16] |
NOH K, PARDO D, TORRES-VERDÍN C. Physics-guided deep-learning inversion method for the interpretation of noisy logging-while-drilling resistivity measurements[J]. Geophysical Journal International, 2023, 235(1): 150-165. |
| [17] |
NOH K, PARDO D, TORRES-VERDÍN C. 2.5-D deep learning inversion of LWD and Deep-Sensing EM measurements across formations with dipping faults[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5.
|
| [18] |
SHAHRIARI M, PARDO D, RIVERA J A, et al. Error control and loss functions for the deep learning inversion of borehole resistivity measurements[J]. International Journal for Numerical Methods in Engineering, 2021, 122(6): 1629-1657. |
| [19] |
COLOMBO D, TURKOGLU E, LI W, et al. Physics-driven deep-learning inversion with application to transient electromagnetics[J]. Geophysics, 2021, 86(3): E209-E224. |
| [20] |
LIU W, WANG H, XI Z, et al. Physics-Driven deep learning inversion with application to magnetotelluric[J]. Remote Sensing, 2022, 14(13): 3218. |
| [21] |
张盼, 邓少贵, 胡旭飞, 等. 超深随钻方位电磁波测井探测特性及参数敏感性分析[J]. 地球物理学报, 2021, 64(6): 2210-2219. ZHANG Pan, DENG Shaogui, HU Xufei, et al. Detection performance and sensitivity of logging-whiledril-ling extra-deep azimuthal resistivity measurement[J]. Chinese Journal of Geophysics, 2021, 64(6): 2210-2219. |
| [22] |
DAVYDYCHEVA S. Two triaxial induction tools: sensitivity to radial invasion profile: Two triaxial induction tools[J]. Geophysical Prospecting, 2011, 59(2): 323-340. |
| [23] |
ZHANG R, LIU Y, SUN H. Physics-guided convolutional neural network (PhyCNN) for data-driven seismic response modeling[J]. Engineering Structures, 2020, 215: 110704. |
| [24] |
WU X, MA J, SI X, et al. Sensing prior constraints in deep neural networks for solving exploration geophysical problems[J]. Proceedings of the National Academy of Sciences of the United States of America, 2023, 120(23): e2219573120. |
| [25] |
KLINE D M, BERARDI V L. Revisiting squared-error and cross-entropy functions for training neural network classifiers[J]. Neural Computing & Applications, 2005, 14(4): 310-318. |
| [26] |
HE K, ZHANG X, REN S, et al. Identity mappings in deep residual networks[C]. Computer Vision - ECCV 2016, Lecture Notes in Computer Science, Springer, Cham, 2016, 630-645.
|
| [27] |
CHEN Z, XIE Z, ZHANG W, et al. ResNet and model fusion for automatic spoofing detection[C]. Interspeech 2017, 2017, 102-106.
|
| [28] |
HE F, LIU T, TAO D. Why ResNet works? residuals generalize[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(12): 5349-5362. |
| [29] |
SCHMIDT-HIEBER J. Nonparametric regression using deep neural networks with ReLU activation function[J]. The Annals of Statistics, 2020, 48(4): 1875-1897. |
| [30] |
KEY K. MARE2DEM: a 2-D inversion code for controlled-source electromagnetic and magnetotelluric data[J]. Geophysical Journal International, 2016, 207(1): 571-588. |
| [31] |
NAKAGAWA S N H, JOHNSON P C D, SCHIELZETH H. The coefficient of determination R2 and intra-class correlation coefficient from genera-lized linear mixed-effects models revisited and expanded[J]. Journal of the Royal Society Interface, 2017, 14(134): 20170213. |



 秦策, 河南省焦作市山阳区世纪大道2001号河南理工大学物理与电子信息学院,454000。Email:
秦策, 河南省焦作市山阳区世纪大道2001号河南理工大学物理与电子信息学院,454000。Email: