2. 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266061
2. Evaluation and Detection Technology Laboratory of Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266061, China
地下介质的速度建模是地震资料成像的重要环节。全波形反演(FWI)充分利用了地震波的运动学和动力学信息,是目前速度建模精度和分辨率最高的方法。Tarantola[1]最早提出了时间域FWI,它通过最小化计算地震数据和观测地震数据之间的残差迭代更新速度模型[2-5]。
拖缆资料的FWI是海洋地震勘探具有潜力的速度建模方式之一。由于受仪器设备的限制,采集到的拖缆资料通常缺少可靠的低频成分。而FWI是复杂的非线性问题,其效果严重依赖于有效的低频地震数据。这导致拖缆资料的FWI发生周期跳跃现象,目标函数收敛到局部极小值,无法获得准确的速度模型。为此,学者们提出了许多改进的波形反演方法,这些方法可以概括为两类。第一类方法为构建非线性程度较低的目标函数。Shin等[6]提出Laplace域FWI方法,将地震数据变换到Laplace域,并与观测的地震数据进行拟合计算,构建FWI的目标函数[7-8]。地震数据在Laplace域具有更多低频成分,目标函数非线性程度更低,但此类方法严重依赖于Laplace衰减常数的选取和大炮检距地震数据。Choi等[9]利用观测地震数据与计算地震数据的全局互相关构建FWI的目标函数,在反演中使观测地震数据和计算地震数据的相位相互匹配。与常规目标函数相比,相位匹配的非线性程度较低[10]。Bozdağ等[11]使用地震数据的包络建立FWI的目标函数,即使地震数据缺少低频信息,地震数据的包络仍然具有丰富的低频信息[12-14]。
第二类方法是重构观测的低频地震数据。Warner等[15]提出通过非线性插值方法从高频地震数据中合成低频数据,并应用于三维海底电缆资料的FWI,获得了较准确的低波数模型。但当噪声能量增大时,由插值生成的低频数据质量急剧下降。Zhang等[16]通过提取被动源地震数据中的低频信息重构主动源地震数据的低频部分,但是被动源地震受噪声严重干扰,重构效果无法保证[17]。陈生昌等[18]提出对散射波场进行时间二阶积分运算重构低频地震数据,由于对波场的二阶时间积分相当于低通滤波,此方法仅适用于散射波场具有一定的低频信息的情况。Zhang等[19]提出通过盲反褶积重构低频地震数据的方法,但是当初始地震子波不够准确时,盲反褶积计算出的反射系数序列存在较大误差,重构的地震数据不够可靠。上述方法都是通过数学运算方式恢复的“数值低频”,与物理意义上的低频数据仍有一定差异。
与人工重构得到的低频数据相比,实际采集到的低频数据更具可靠性。OBN(海底节点)/OBS(海底地震仪)资料的另一个优势是宽方位角采集,能够提供大炮检距地震数据,对高陡构造以及地下介质深部的反演具有关键作用[20-21]。
另外,FWI的效果强烈依赖于准确的震源子波。当观测地震数据的震源子波与反演使用的震源子波不匹配时,反演效果急剧变差。然而,实际采集到的地震资料中,震源子波是未知的,在拖缆与OBN资料的联合反演中,由于两种地震资料的震源子波存在差异,因此反演结果受震源子波的影响更加严重。因为OBS资料中含有丰富的低频成分,Yang等[22]使用OBS资料与拖缆资料进行联合波形反演,但因未考虑子波差异的影响导致反演结果不佳。为此,学者们开发了不依赖震源子波的FWI方法。Lee等[23]提出了使用单一参考道对频率域地震记录进行归一化处理;Zhou等[24]提出了使用单炮平均振幅进行归一化处理。在频率域进行归一化处理,能够消除目标函数中的震源子波项,达到不依赖震源子波的目的。Choi等[25]提出在频率域将模拟数据与观测数据分别与对方的参考道相乘,使目标函数中具有相同的震源子波项,消除震源子波不匹配的影响。后来,Choi等 [26]将参考道方法从频率域推广到时间域,模拟数据与观测数据分别与对方的参考道褶积。此外,辛天亮等[27]提出了基于数据相似性的频率域全波形反演方法,也达到了不依赖震源子波的效果。
本文提出一种不依赖震源子波的海洋拖缆与OBN资料联合全波形反演方法。通过含有丰富低频数据的OBN资料与拖缆资料联合反演,消除因拖缆资料低频缺失造成的周期跳跃。利用时间域的平均道方法进行联合反演不依赖于震源子波,并且与传统的参考道方法相比,平均道方法具有更好的抗噪性。用Marmousi模型合成的拖缆资料与OBN资料完成模型测试,结果验证了本文方法的可行性和有效性。
1 方法原理 1.1 目标函数传统FWI的目标函数定义为观测地震数据与计算地震数据残差的二范数[28]。由于实际采集的拖缆资料常常缺少可靠的低频数据,单独进行FWI时容易发生周期跳跃,因此需要与OBN资料联合反演,此时目标函数为
| $ \begin{array}{l}E\left(v\right)=\frac{{\alpha }_{1}}{2}\sum\limits_{s}\sum\limits_{g}{‖{\boldsymbol{d}}_{\mathrm{c}\mathrm{a}\mathrm{l}}^{\mathrm{T}\mathrm{S}}({\boldsymbol{x}}_{g}, {\boldsymbol{x}}_{s})-{\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}^{\mathrm{T}\mathrm{S}}({\boldsymbol{x}}_{g}, {\boldsymbol{x}}_{s})‖}_{2}^{2}+\\ \frac{{\alpha }_{2}}{2}\sum\limits_{s}\sum\limits_{o}{‖{\boldsymbol{d}}_{\mathrm{c}\mathrm{a}\mathrm{l}}^{\mathrm{O}\mathrm{B}\mathrm{N}}({\boldsymbol{x}}_{o}, {\boldsymbol{x}}_{s})-{\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}^{\mathrm{O}\mathrm{B}\mathrm{N}}({\boldsymbol{x}}_{o}, {\boldsymbol{x}}_{s})‖}_{2}^{2}\end{array} $ | (1) |
式中:v为速度;s为震源序号;g为拖缆的检波器序号;xg为检波器的空间坐标;o为OBN序号;xo为OBN的空间坐标;dcal与dobs分别是计算地震数据与观测地震数据;上标TS和OBN分别表示拖缆资料与OBN资料;xs为震源的空间位置;α1和α2分别为拖缆资料和OBN资料在联合反演中的权重。
由于采用了从低频到高频的多尺度反演策略,为了让OBN资料在反演前期发挥作用,弥补拖缆资料的低频缺失,权重设置如下
| $ {\alpha }_{1}=\frac{k}{n} $ | (2) |
| $ {\alpha }_{2}=\frac{n-k}{n} $ | (3) |
式中:k为当前迭代次数;n为反演的总迭代次数。这样设置能够使OBN资料的权重α2在反演速度模型的低波数分量时取较大的值,对速度模型的更新影响较大。
上述联合反演是建立在震源子波已知的情况下,而实际勘探中震源子波是未知的。传统不依赖震源子波的反演方法基于参考道实现,将观测数据与计算数据分别与对方的参考道进行褶积。但是参考道方法严重依赖于参考道的选取,并且与参考道褶积的过程会导致反演抗噪性降低。因此本文用平均道代替参考道,一方面避免了参考道的选取问题,另一方面求取平均道的过程一定程度上压制了地震数据中的随机噪声。
基于平均道的全波形反演目标函数定义为
| $ E=\sum\limits_{i=1}^{{N}_{\mathrm{s}}}\sum\limits_{j=1}^{{N}_{\mathrm{r}}}{‖{\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}-{\boldsymbol{d}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}‖}_{2}^{2} $ | (4) |
式中:
| $ {\boldsymbol{A}}_{i}=\frac{1}{{N}_{\mathrm{r}}}\sum\limits_{j=1}^{{N}_{\mathrm{r}}}{\boldsymbol{d}}_{i, j} $ | (5) |
平均道方法不依赖震源子波的原理与单一参考道类似。将式(4)中的地震数据写成震源子波与格林函数褶积的形式,即
| $ E=\sum\limits_{i=1}^{{N}_{\mathrm{s}}}\sum\limits_{j=1}^{{N}_{\mathrm{r}}}‖{\boldsymbol{s}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}{\boldsymbol{G}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}\left(\frac{1}{{N}_{\mathrm{r}}}\sum\limits_{j=1}^{{N}_{\mathrm{r}}}{\boldsymbol{s}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}{\boldsymbol{G}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\right)- \\{{\boldsymbol{s}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}{\boldsymbol{G}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}\left(\frac{1}{{N}_{\mathrm{r}}}\sum\limits_{j=1}^{{N}_{\mathrm{r}}}{\boldsymbol{s}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}{\boldsymbol{G}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\right)‖}_{2}^{2} $ | (6) |
式中:si为震源子波;
由于褶积运算满足分配律和交换律,式(6)可变形为
| $ E=\sum\limits_{i=1}^{{N}_{\mathrm{s}}}\sum\limits_{j=1}^{{N}_{\mathrm{r}}}‖{\boldsymbol{s}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}{\boldsymbol{s}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}{\boldsymbol{G}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}\left(\frac{1}{{N}_{\mathrm{r}}}\sum\limits_{j=1}^{{N}_{\mathrm{r}}}{\boldsymbol{G}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\right)- \\ {{\boldsymbol{s}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}{\boldsymbol{s}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}{\boldsymbol{G}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}\left(\frac{1}{{N}_{\mathrm{r}}}\sum\limits_{j=1}^{{N}_{\mathrm{r}}}{\boldsymbol{G}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\right)‖}_{2}^{2} $ | (7) |
式(7)中做差的两项具有相同的新震源子波siobs*sical,因此消除了反演中震源子波的不匹配影响,达到不依赖震源子波的效果。由此可以建立基于平均道的不依赖震源子波的拖缆和OBN资料联合FWI目标函数
| $ \begin{aligned} E(v)= & \frac{\alpha_1}{2} \sum_s \sum_g \| \boldsymbol{d}_{\mathrm{cal}}^{\mathrm{TS}}\left(\boldsymbol{x}_g, \boldsymbol{x}_s\right) * \boldsymbol{A}_{\mathrm{obs}}^{\mathrm{TS}}\left(\boldsymbol{x}_s\right)- \\ & \boldsymbol{d}_{\mathrm{obs}}^{\mathrm{TS}}\left(\boldsymbol{x}_g, \boldsymbol{x}_s\right) * \boldsymbol{A}_{\mathrm{cal}}^{\mathrm{TS}}\left(\boldsymbol{x}_s\right) \|_2^2+ \\ & \frac{\alpha_2}{2} \sum_s \sum_o \| \boldsymbol{d}_{\mathrm{cal}}^{\mathrm{OBN}}\left(\boldsymbol{x}_o, \boldsymbol{x}_s\right) * \boldsymbol{A}_{\mathrm{obs}}^{\mathrm{OBN}}\left(\boldsymbol{x}_s\right)- \\ & \boldsymbol{d}_{\mathrm{obs}}^{\mathrm{OBN}}\left(\boldsymbol{x}_o, \boldsymbol{x}_s\right) * \boldsymbol{A}_{\mathrm{cal}}^{\mathrm{OBN}}\left(\boldsymbol{x}_s\right) \|_2^2 \end{aligned} $ | (8) |
本文使用常密度声波方程进行正演模拟
| $ \frac{1}{{v}^{2}\left(\boldsymbol{x}\right)}\frac{{\partial }^{2}p(\boldsymbol{x}, t\left|{\boldsymbol{x}}_{s}\right.)}{\partial {t}^{2}}-{\nabla }^{2}p(\boldsymbol{x}, t\left|{\boldsymbol{x}}_{s}\right.)={f}_{\mathrm{s}}(\boldsymbol{x}, t\left|{\boldsymbol{x}}_{s}\right.) $ | (9) |
式中:x为空间位置;t为时间;p为波场;fs为地震子波。使用与褶积重构低频地震数据相同的地震子波。正演时使用规则网格有限差分正演,时间上为2阶精度,空间上为12阶精度。使用完全匹配层方法以消除边界反射。
1.3 局部优化算法最小化目标函数时,使用共轭梯度法[29],即通过求取目标函数的共轭梯度计算目标函数的下降方向。目标函数的共轭梯度由下式求得
| $ \boldsymbol{d}{}_{k}(\boldsymbol{x})=\left\{\begin{array}{l}-\nabla {E}_{0}\left(\boldsymbol{x}\right) \;\;\;\;\;\;\;k=0\\ -\nabla {E}_{k}\left(\boldsymbol{x}\right)+{\beta }_{k}{\boldsymbol{d}}_{k-1}\left(\boldsymbol{x}\right)k > 0\end{array}\right. $ | (10) |
式中参数
| $ {\beta }_{k}=\frac{〈\nabla {E}_{k}, \nabla {E}_{k}〉}{〈{\boldsymbol{d}}_{k-1}, \nabla {E}_{k}-\nabla {E}_{k-1}〉} $ | (11) |
联合反演目标函数的梯度为拖缆与OBN资料各自的梯度加权后求和
| $ \nabla E\left(\boldsymbol{x}\right)={\alpha }_{1}{\boldsymbol{G}}^{\mathrm{T}\mathrm{S}}\left(\boldsymbol{x}\right)+{\alpha }_{2}{\boldsymbol{G}}^{\mathrm{O}\mathrm{B}\mathrm{N}}\left(\boldsymbol{x}\right) $ | (12) |
式中
| $ \nabla E\left(x\right)=\mathrm{R}\mathrm{e}\left[\sum\limits_{s}\sum\limits_{\omega }{\omega }^{2}{p}_{\mathrm{b}}^{\mathrm{*}}(\boldsymbol{x}, \omega \left|{\boldsymbol{x}}_{s}\right.){p}_{\mathrm{f}}(\boldsymbol{x}, \omega \left|{\boldsymbol{x}}_{s}\right.)\right] $ | (13) |
式中:Re表示取复数的实部;
正传波场的震源在炮点位置,震源子波是重构低频地震数据使用的子波。反传波场的震源在检波点位置,反传震源由伴随状态法[31]推导(推导过程见附录A)得到
| $ {\boldsymbol{r}}_{i, j}^{\text{'}}={\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\otimes \left({\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}-{\boldsymbol{d}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}\right) $ | (14) |
| $ {\boldsymbol{r}}_{i, j}^{″}=-{\boldsymbol{d}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\otimes \left({\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}-{\boldsymbol{d}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}\right) $ | (15) |
式中:
计算出共轭梯度之后,对速度模型
| $ {v}_{k+1}\left(\boldsymbol{x}\right)={v}_{k}\left(\boldsymbol{x}\right)+{\alpha }_{k}{\boldsymbol{d}}_{k}\left(\boldsymbol{x}\right) $ | (16) |
式中αk是速度模型第
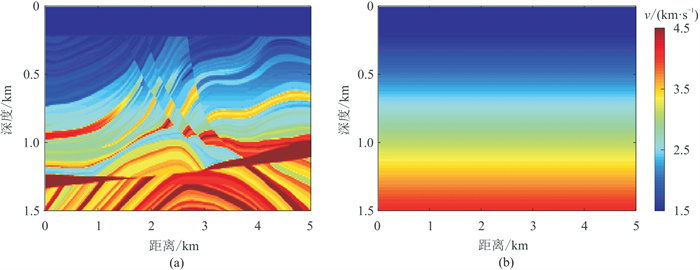
为了验证本文方法的可行性与有效性,用Marmousi模型(图 1)合成数据进行测试。模型尺寸为5.0 km×1.5 km,模型的速度范围为1.5~4.5 km/s。使用的初始速度模型与真实速度模型相差较大,速度随深度呈线性变化,速度范围为1.50~4.03 km/s。在模型上表面共激发50炮,炮间距为100 m。拖缆资料由500个水听器以10 m间距在水面同时接收,OBN资料由10个OBN以500 m间距在海底同时接收。进行正演模拟时,合成拖缆资料的震源子波主频为15 Hz,合成OBN资料的震源子波主频为8 Hz,因为实际勘探中OBN资料主频比拖缆资料低,为了模拟低频缺失的拖缆资料,对合成的拖缆资料进行5 Hz的高通滤波。
|
图 1 Marmousi模型的理论速度模型(a)和初始速度模型(b) |
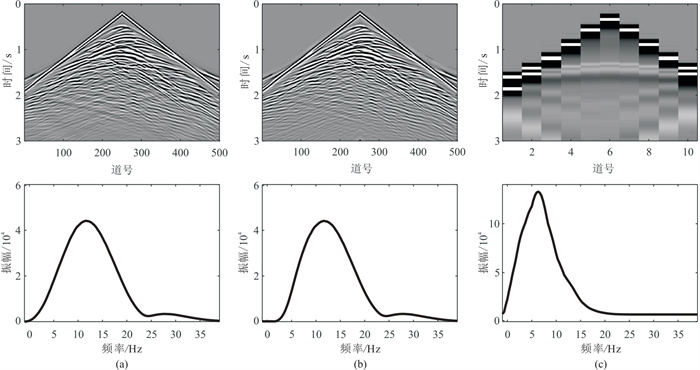
图 2为模拟的拖缆资料以及OBN资料。从频谱可知,合成的OBN地震资料含有丰富的5 Hz以下的低频数据。
|
图 2 Marmousi模型合成的地震记录(上)及其频谱(下) (a)合成的拖缆数据;(b)高通滤波后的拖缆数据;(c)合成的OBN数据 |
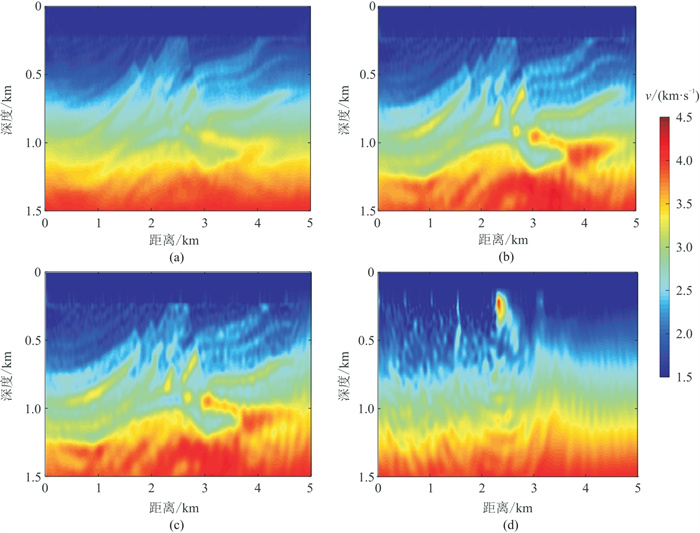
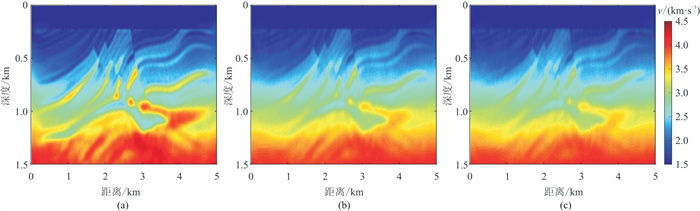
对滤除低频的拖缆资料进行FWI,反演使用的8个频率分别为2、3、4.5、6.3、8.82、12.348、17.2872和24.2021 Hz,每个频率迭代10次,得到图 3a所示结果。对不同间距的OBN数据进行FWI,反演使用的8个频率分别为1、1.4、1.96、2.744、3.8416、5.3782、7.5295和10.5414 Hz,每个频率迭代10次。OBN资料间距分别为500、1000、1500 m时,反演结果如图 3b~图 3d所示。由图可见,使用缺失低频部分的拖缆资料单独进行FWI,反演结果中出现了局部极小值现象,无法得到准确的反演结果。单独使用OBN资料进行反演时,由于其覆盖次数不足,无法反演速度模型高分辨率部分,并且随着OBN间距增大到1500 m,反演出现严重错误。不同间距的OBN资料与拖缆资料进行联合反演时使用的频率和迭代次数与单一资料反演相同。OBN资料间距分别为500、1000、1500 m时,联合反演结果如图 4所示。由图可见,联合反演结果的效果得到显著提高。但当OBN间距过大时,OBN资料对反演的改善作用不明显。
|
图 3 单一地震资料FWI结果 (a)滤波后的拖缆资料;(b)500 m间距OBN资料;(c)1000 m间距OBN资料;(d)1500 m间距OBN资料 |
|
图 4 拖缆与不同间距OBN资料联合FWI结果 (a)与500 m间距OBN资料联合;(b)与1000 m间距OBN资料联合;(c)与1500 m间距OBN资料联合 |
本文FWI采用基于MPI的炮并行运算策略,模型测试中,单一资料FWI约耗时2.1 h,联合FWI约耗时3.5 h。
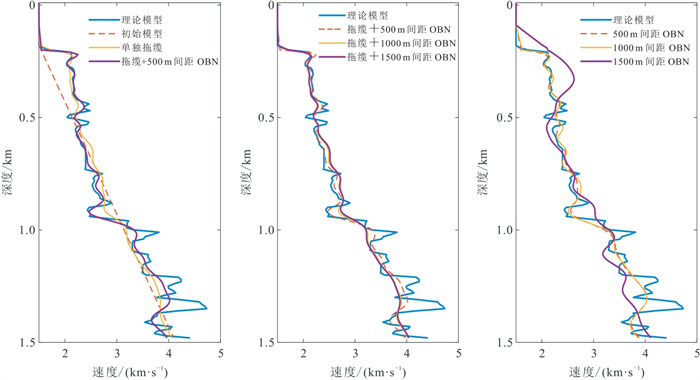
图 5对比了理论模型、初始速度模型和几种反演方法的反演结果于水平方向2.5 km处速度随深度变化的曲线。从速度—深度曲线对比也能够看出:拖缆与OBN资料联合FWI结果比两种资料单独反演结果更接近真实模型。随着OBN间距增大,联合FWI效果逐渐变差。
|
图 5 水平方向2.5 km处速度—深度曲线对比 |
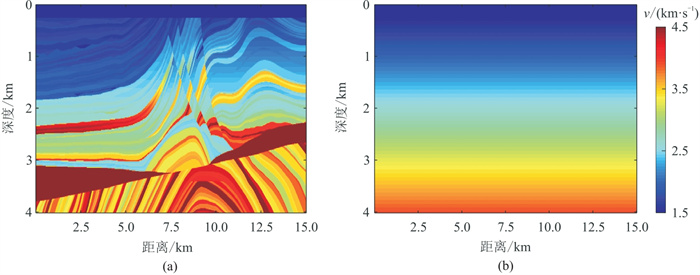
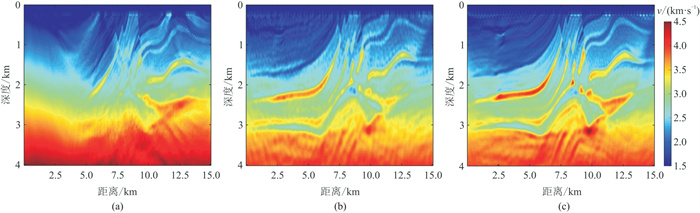
另外,为了验证联合FWI中OBN资料大炮检距的作用,使用尺寸为15 km×4 km的Marmousi模型进行了测试。拖缆资料采用单边接收,缆线长度为6 km,OBN以500 m间距布设在模型的整个海底位置。拖缆资料道间距为12.5 km,炮点设置在水平方向6~15 km位置的海面,炮间距125 m,拖缆与OBN同时采集。图 6为理论模型与初始模型。分别使用拖缆资料、OBN资料以及拖缆与OBN联合三种方式进行反演,得到图 7所示结果。由图 7a的拖缆资料FWI结果可以看出,在炮检距受限制的情况下,模型深部以及水平方向7~12 km处的高陡构造反演效果较差。图 7b的OBN资料FWI结果中,由于OBN布设稀疏,导致反演模型的分辨率较低。当两种资料进行联合FWI,得到图 7c所示结果,较好地反演了模型深部和高陡构造,相比图 7b结果分辨率更高。
|
图 6 大尺寸的Marmousi速度模型(a)和初始速度模型(b) |
|
图 7 图 6模型的FWI结果 (a)拖缆数据;(b)OBN数据;(c)拖缆与OBN数据联合 |
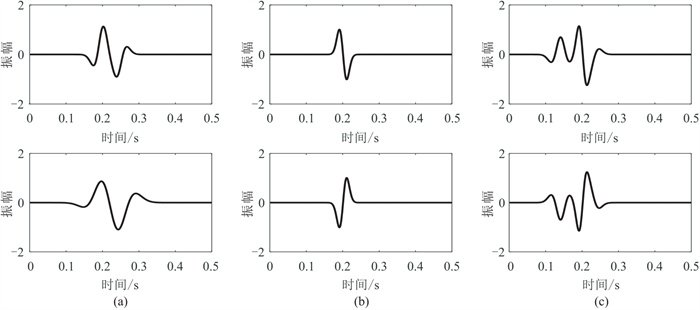
上述测试是建立在合成资料与反演使用相同震源子波的基础上,为了测试基于平均道的不依赖震源子波的联合反演方法的可行性与有效性,在反演中使用与合成地震数据不同的子波。采用三组子波进行正演,分别合成拖缆与OBN数据。第一组为将不同振幅(图 8a上)和相位(图 8a下)的Ricker子波叠加得到的新子波;第二组为高斯函数的一阶导数(图 8b上)及其相反数(图 8b下);第三组为复杂子波(图 8c上)及其相反数(图 8c下)。对每组子波合成的地震数据分别用式(1)目标函数的传统联合FWI方法和本文提出的不依赖震源子波联合FWI方法进行对比实验,反演中正演模拟拖缆数据和OBN数据的震源子波使用主频分别为15 Hz和8 Hz的Ricker子波。反演结果如图 9所示。
|
图 8 合成地震数据使用的震源子波 (a)第一组子波;(b)第二组子波;(c)第三组子波 |
|
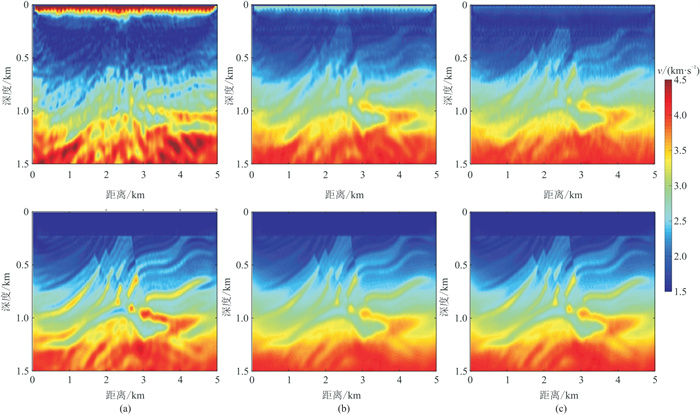
图 9 反演子波与地震数据子波不一致时的反演结果对比 (a)第一组子波合成数据常规联合FWI(上)与平均道联合FWI(下)结果;(b)第二组子波合成数据常规联合FWI(上)与平均道联合FWI(下)结果;(c)第三组子波合成数据常规联合FWI(上)与平均道联合FWI(下)结果 |
由图 9可知,在联合反演中引入平均道方法,即使反演使用的子波与地震数据子波不一致,仍然能够得到正确的反演结果,说明反演可以不依赖震源子波。基于三组子波合成地震数据的对比实验证明了本文所提方法能够解决常规联合FWI中子波不匹配的问题。
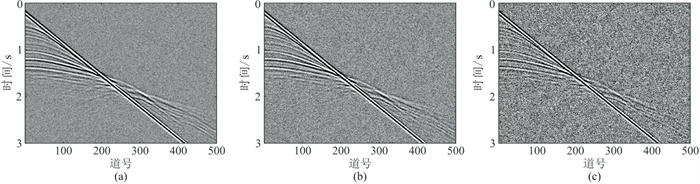
2.3 含噪数据测试为了测试基于平均道的联合FWI方法在含噪数据中的优势,在合成的拖缆数据中加入不同信噪比(S/N)的高斯噪声。然后在合成地震数据子波与反演子波不一致时,分别使用单一参考道方法、平均道方法进行全波形反演,对两种反演方法的结果进行对比。单一参考道方法的反演实验中,选取最小炮检距的地震道作为参考道。图 10为加入不同比例噪声后的拖缆地震数据。图 11为基于单一参考道方法和基于平均道方法的反演结果。由图可知,当地震数据含噪时,使用单一参考道方法进行反演,受噪声影响严重。使用平均道方法时,由于求平均道的过程一定程度上压制了随机噪声,因此反演结果优于单一参考道方法。结果对比证明,在各噪声条件下,基于平均道的全波形反演方法对于随机噪声均具有更好的抗噪性。当噪声过强时,两种方法效果均受影响严重,平均道方法效果仍优于单一参考道方法。
|
图 10 添加不同程度噪声的拖缆地震记录 (a)S/N=4.64;(b)S/N=3.25;(c)S/N=0.24 |

|
图 11 含有不同噪声地震数据单一参考道FWI(a)和平均道FWI(b)结果对比 左:S/N=4.64;中:S/N=3.25;右:S/N=0.24 |
全波形反演是一个强非线性问题,局部优化算法容易陷入局部极小值。当观测地震数据缺少低频,初始速度模型不够准确时,往往得到错误的反演结果。现有的拓频方法大多是通过数学变换获取地震数据的数值低频,缺少物理意义上的联系。使用本身含有丰富低频数据的少量OBN资料与拖缆资料进行联合全波形反演,能够很好地解决拖缆地震资料的低频缺失,压制周期跳跃现象。本文提出了基于平均道方法的海洋拖缆与OBN资料联合波形反演方法。Marmousi模型测试表明,利用本文方法引入OBN资料解决了拖缆资料低频缺失问题,利用平均道褶积方法,使反演不依赖震源子波,压制了子波不匹配引起的反演错误,达到了不依赖震源子波的效果。另外,测试还表明与传统的基于单一参考道反演相比,基于平均道的反演方法在面对含噪数据时具有更好的抗噪性。
因无同时采集的拖缆和OBN资料,未进行实测资料测试。
附录A 不依赖震源子波的目标函数梯度计算基于平均道的不依赖震源子波的目标函数为
| $ E=\sum\limits_{i=1}^{{N}_{\mathrm{s}}}\sum\limits_{j=1}^{{N}_{\mathrm{r}}}{‖{\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}-{\boldsymbol{d}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}‖}_{2}^{2} $ | (A-1) |
将上式对模型求偏导可得
| $ \frac{\partial E}{\partial \boldsymbol{m}}=\sum\limits_{i=1}^{{N}_{\mathrm{s}}}\sum\limits_{j=1}^{{N}_{\mathrm{r}}}\left[\left(\frac{\partial {\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}}{\partial \boldsymbol{m}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\right)\cdot {\boldsymbol{r}}_{i, j}-\left({\boldsymbol{d}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}\frac{\partial {\boldsymbol{A}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}}{\partial \boldsymbol{m}}\right)\cdot {\boldsymbol{r}}_{i, j}\right] $ | (A-2) |
式中:m为模型参数;
| $ \begin{array}{l}\left(\frac{\partial {\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}}{\partial \boldsymbol{m}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\right)\cdot {\boldsymbol{r}}_{i, j}\\ \;\;\;\;\;\;\;\;={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left[\frac{\partial {\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}}{\partial \boldsymbol{m}}\left(t-\tau \right){\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\left(\tau \right){\boldsymbol{r}}_{i, j}\left(t\right)\right]\mathrm{d}\tau \mathrm{d}t\end{array} $ | (A-3) |
令
| $ \left(\frac{\partial {\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}}{\partial \boldsymbol{m}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\right)\cdot {\boldsymbol{r}}_{i, j}=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\partial {\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}}{\partial \boldsymbol{m}}\left(\xi \right){\boldsymbol{r}}_{i, j}^{\text{'}}\left(\xi \right)\mathrm{d}\xi $ | (A-4) |
式中:
| $ \begin{array}{l}\left(\frac{\partial {\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}}{\partial \boldsymbol{m}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\right)\cdot {\boldsymbol{r}}_{i, j}\\ =-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left[{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\boldsymbol{V}}_{i, x}^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(\xi -\tau \right){\boldsymbol{G}}_{x, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(\tau \right)\mathrm{d}\tau \right]{\boldsymbol{r}}_{i, j}^{\text{'}}\left(\xi \right)\mathrm{d}\xi \end{array} $ | (A-5) |
再令
| $ \begin{array}{l}\left(\frac{\partial {\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}}{\partial \boldsymbol{m}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\right)\cdot {\boldsymbol{r}}_{i, j}\\ ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\boldsymbol{V}}_{i, \boldsymbol{x}}^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)\left[{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\boldsymbol{G}}_{\boldsymbol{x}, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(\xi -t\right){\boldsymbol{r}}_{i, j}^{\text{'}}\left(\xi \right)\mathrm{d}\xi \right]\mathrm{d}t\end{array} $ | (A-6) |
根据互易定理,格林函数
| $ \begin{array}{l}-\left({\boldsymbol{d}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}\frac{\partial {\boldsymbol{A}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}}{\partial \boldsymbol{m}}\right)\cdot {\boldsymbol{r}}_{i, j}\\ ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\boldsymbol{V}}_{i, \boldsymbol{x}}^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(t\right)\left[{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\boldsymbol{G}}_{\boldsymbol{x}, k}^{\mathrm{c}\mathrm{a}\mathrm{l}}\left(\xi -t\right){\boldsymbol{r}}_{i, j}^{″}\left(\xi \right)\mathrm{d}\xi \right]\mathrm{d}t\end{array} $ | (A-7) |
式中
综上所述,求取梯度所需要的反传震源可以根据
| $ {\boldsymbol{r}}_{i, j}^{\text{'}}={\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}\otimes \left({\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}-{\boldsymbol{d}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}\right) $ | (A-8) |
| $ {\boldsymbol{r}}_{i, j}^{″}=-{\boldsymbol{d}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\otimes \left({\boldsymbol{d}}_{i, j}^{\mathrm{c}\mathrm{a}\mathrm{l}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{o}\mathrm{b}\mathrm{s}}-{\boldsymbol{d}}_{i, j}^{\mathrm{o}\mathrm{b}\mathrm{s}}\mathrm{*}{\boldsymbol{A}}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}\right) $ | (A-9) |
| [1] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 19(8): 1259-1266. |
| [2] |
PRATT R G. Frequency-domain elastic wave modeling by finite differences: A tool for crosshole seismic imaging[J]. Geophysics, 1990, 55(5): 626-632. |
| [3] |
BUNKS C, SALECK F M, ZALESKI S. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473. |
| [4] |
SIRGUE L, PRATT R G. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies[J]. Geophysics, 2003, 69(1): 231-248. |
| [5] |
PRIEUX V, LAMBARÉ G, OPERTO S, et al. Building starting model for full waveform inversion from wide-aperture data by stereotomography[J]. Geophysical Prospecting, 2013, 61(S1): 109-137. |
| [6] |
SHIN C, CHA Y H. Waveform inversion in the Laplace domain[J]. Geophysical Journal International, 2008, 173(3): 922-931. |
| [7] |
JUN H, KIM Y, SHIN J, et al. Laplace-Fourier-domain elastic full‑waveform inversion using time‑domain modeling[J]. Geophysics, 2014, 79(5): R195-R208. |
| [8] |
郭啟民, 何兵寿, 史才旺. 低频缺失数据的弹性波全波形反演策略[J]. 中国海洋大学学报(自然科学版), 2020, 50(7): 108-116. GUO Qimin, HE Bingshou, SHI Caiwang. Full waveform inversion strategy of elastic wave with low frequency missing data[J]. Periodical of Ocean University of China, 2020, 50(7): 108-116. |
| [9] |
CHOI Y, ALKHALIFAH T. Application of multi-source waveform inversion to marine streamer data using the global correlation norm[J]. Geophysical Prospecting, 2012, 60(4): 748-758. |
| [10] |
梁煌, 韩立国, 许卓, 等. 互相关与最小二乘加权目标函数全波形反演[J]. 世界地质, 2017, 36(2): 588-594. LIANG Huang, HAN Liguo, XU Zhuo, et al. Full waveform inversion based on weighted cross-correlation and least squares objective function[J]. Global Geology, 2017, 36(2): 588-594. |
| [11] |
BOZDAĞ E, TRAMPERT J, TROMP J. Misfit functions for full waveform inversion based on instantaneous phase and envelope measurements[J]. Geophysical Journal International, 2011, 185(2): 845-870. |
| [12] |
CHI B, DONG L, LIU Y. Full waveform inversion method using envelope objective function without low frequency data[J]. Journal of Applied Geophysics, 2014, 109: 36-46. |
| [13] |
WU R, LUO J, WU B. Seismic envelope inversion and modulation signal model[J]. Geophysics, 2014, 79(3): WA13-WA24. |
| [14] |
CHI B, DONG L, LIU Y. Full waveform inversion based on envelope objective function[C]. Extended Abstracts of 75th EAGE Conference & Exhibition, 2013, cp-348-00152.
|
| [15] |
WARNER M, NANGOO T N E, SHAH N, et al. Full‑waveform inversion of cycle-skipped seismic data by frequency down-shifting[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 903-907.
|
| [16] |
ZHANG P, HAN L G, ZHOU Y, et al. Passive-source multitaper-spectral method based low-frequency data reconstruction for active seismic sources[J]. Applied Geophysics, 2015, 12(4): 585-597. |
| [17] |
毛博, 韩立国. 基于相似性重构低频数据的金属矿频域全波形反演[J]. 地球物理学报, 2019, 62(10): 4010-4019. MAO Bo, HAN Liguo. Full waveform inversion in the frequency domain of low-frequency seismic data based on similarity reconstruction for exploration of deep metallic ores[J]. Chinese Journal of Geophysics, 2019, 62(10): 4010-4019. |
| [18] |
陈生昌, 陈国新. 时间二阶积分波场的全波形反演[J]. 地球物理学报, 2016, 59(10): 3765-3776. CHEN Shengchang, CHEN Guoxin. Full waveform inversion of the second-order time integral wavefield[J]. Chinese Journal of Geophysics, 2016, 59(10): 3765-3776. |
| [19] |
ZHANG P, HAN L, XU Z, et al. Sparse blind deconvolution based low-frequency seismic data reconstruction for multiscale full waveform inversion[J]. Journal of Applied Geophysics, 2017, 139: 91-108. |
| [20] |
BROSSIER R, OPERTO S, VIRIEUX J. Velocity model building from seismic reflection data by full-waveform inversion[J]. Geophysical Prospecting, 2015, 63(2): 354-367. |
| [21] |
LANZARONE P, SHEN X, BRENDERS A, et al. Innovative application of full-waveform inversion applied to extended wide-azimuth marine streamer seismic data in a complex salt environment[J]. Geophysics, 2022, 87(3): B193-B205. |
| [22] |
YANG H, ZHANG J. Full waveform inversion of combined towed streamer and limited OBS seismic data: a theoretical study[J]. Marine Geophysical Research, 2019, 40(3): 237-244. |
| [23] |
LEE K H, KIM H J. Source-independent full-waveform inversion of seismic data[J]. Geophysics, 2003, 68(6): 2010-2015. |
| [24] |
ZHOU B, GREENHALGH S A. Crosshole seismic inversion with normalized full‑waveform amplitude data[J]. Geophysics, 2003, 68(4): 1320-1330. |
| [25] |
CHOI Y, SHIN C, MIN D J, et al. Efficient calculation of the steepest descent direction for source-independent seismic waveform inversion: An amplitude approach[J]. Journal of Computational Physics, 2005, 208(2): 455-468. |
| [26] |
CHOI Y, ALKHALIFAH T. Source-independent time-domain waveform inversion using convolved wavefields: Application to the encoded multisource waveform inversion[J]. Geophysics, 2011, 76(5): R125-R134. |
| [27] |
辛天亮, 黄建平, 解飞, 等. 基于数据相似性的不依赖子波的频率域全波形反演[J]. 石油地球物理勘探, 2020, 55(2): 341-350. XIN Tianliang, HUANG Jianping, XIE Fei, et al. Source‑independent frequency-domain full waveform inversion based on data similarity[J]. Oil Geophysical Prospecting, 2020, 55(2): 341-350. |
| [28] |
TARANTOLA A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 1986, 51(10): 1893-1903. |
| [29] |
FLETCHER R, REEVES C M. Function minimization by conjugate gradients[J]. Computer Journal, 1964, 7(2): 149-154. |
| [30] |
DAI Y H, YUAN Y. A nonlinear conjugate gradient method with a strong global convergence property[J]. SIAM Journal on Optimization, 1999, 10(1): 177-182. |
| [31] |
PLESSIX R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 2006, 167(2): 495-503. |
| [32] |
SAMBRIDGE M S, TARANTOLA A, KENNETT B L N. An alternative strategy for non-linear inversion of seismic waveforms1[J]. Geophysical Prospecting, 1991, 39(6): 723-736. |
| [33] |
VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. |
| [34] |
杨涛, 张会星, 史才旺. 不依赖子波的弹性波混合域全波形反演[J]. 石油地球物理勘探, 2019, 54(2): 348-355. YANG Tao, ZHANG Huixing, SHI Caiwang. Wavelet-independent elastic wave full waveform inversion in hybrid domain[J]. Oil Geophysical Prospecting, 2019, 54(2): 348-355. |
| [35] |
张岩, 周一帆, 宋利伟, 等. 基于物理约束U-Net网络的地震数据低频延拓[J]. 石油地球物理勘探, 2023, 58(1): 31-45. ZHANG Yan, ZHOU Yifan, SONG Liwei, et al. Low frequency continuation of seismic data based on physically constrained U-Net network[J]. Oil Geophysical Prospecting, 2023, 58(1): 31-45. |
| [36] |
徐世刚, 包乾宗, 任志明. 简化的三维TTI介质黏滞纯声波方程及其数值模拟[J]. 石油地球物理勘探, 2022, 57(2): 331-341. XU Shigang, BAO Qianzong, REN Zhiming. Simplified three-dimensional TTI medium viscous pure acoustic wave equation and its numerical simulation[J]. Oil Geophysical Prospecting, 2022, 57(2): 331-341. |



 张建中, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院,266100。Email:
张建中, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院,266100。Email: